|
|
Кгу Индустриальнотехнологический колледж Поурочный план 165166 Усеченный конус и его элементы. Развертка, площадь боковой и полной поверхности усеченного конуса
КГУ «Индустриально-технологический колледж»
Поурочный план № 165-166
Усеченный конус и его элементы. Развертка, площадь боковой и полной поверхности усеченного конуса.
(тема занятия)
Наименование дисциплины: Математика
Подготовил педагог: Тихоненко С.А.
Дата урока: 20.05.2021 года
1. Общие сведения
1.1 Курс, группы: первый, 9СЛ20, 9МК20, 9ОП20
1.2 Тип занятия: комбинированный/ дистанционный
1.3 Межпредметные связи: физика, черчение.
2. Цели, задачи:
Цель урока: Ввести понятие усеченного конуса и его элементов, вывести формулу для вычисления полной поверхности усеченного конуса. Решить задачи по этой теме.
Задачи урока:
формирование понятий усеченного конуса;
формирование умений находить площадь боковой поверхности усеченного конуса, площадь полной поверхности усеченного конуса;
выявить уровень усвоения знаний учащихся по данной теме.
развитие функционального мышления, памяти, внимания, устной и письменной математической речи;
формирование математической речи учащихся и оформление решения задач;
формирование интереса к изучению математики.
воспитание интереса к предмету;
воспитание аккуратности при выполнении чертежей;
воспитание культуры умственного труда, коммуникативной культуры, рефлексивной культуры.
Результаты обучения:
1) Вычислять площади боковой и полной поверхности тел вращения.
2.3 Критерии оценки:
1)Применяет формулы площади боковой поверхности тел вращения при решении задач;
2) Применяет формулы площади полной поверхности тел вращения при решении задач.
3. Оснащение занятия
3.1 Учебно-методическое оснащение: дидактические материалы, справочно-инструктивные таблицы, карточки с заданиями, оценочные листы.
Справочная литература: А.Е.Әбылқасымова, В.Е. Корчевский, З.Ә. Жумагулова, Алгебра и начала анализа: Учебник для 10 классов естественно- математического направления обшеобразовательных школ.1-2 часть. Алматы: Мектеп, 2019г.
3.2 Техническое оснащение, материалы, ИКТ: мультимедийный проектор, ноутбук, экран.
4. Ход занятия
Заплани-
рованные этапы урока, время
|
Деятельность, запланированная на уроке
|
Ресурсы
|
Начало урока
|
Орг. момент.
|
|
|
Проверка домашнего задания.
Фронтальный опрос: Конус и его элементы.
|
Презентация
|
Середина урока
|
https://drive.google.com/file/d/1SpAuXqH38NmLBI6T8KP_uBqVQhuR2PID/view?usp=sharing
http://school-collection.edu.ru/catalog/res/3208b518-f002-4c6a-a8ce-210e81e71261/view/

Рис. 1. Предметы из жизни, имеющие форму усеченного конуса
Как вы думаете, откуда в геометрии берутся новые фигуры? Все очень просто: человек в жизни сталкивается с похожими объектами и придумывает, как бы их назвать. Рассмотрим тумбу, на которой сидят львы в цирке, кусок морковки, который получается, когда мы нарезали только часть ее, действующий вулкан и, например, свет от фонарика (см. рис. 1).

Рис. 2. Геометрические фигуры
Мы видим, что все эти фигуры похожей формы – и снизу, и сверху они ограничены кругами, но они сужаются кверху (см. рис. 2).

Рис. 3. Отсечение верхней части конуса
Это похоже на конус. Только не хватает верхушки. Мысленно представим, что мы берем конус и отсекаем от него верхнюю часть одним взмахом острого меча (см. рис. 3).

Рис. 4. Усеченный конус
Получается как раз наша фигура, называется она усеченный конус (см. рис. 4).
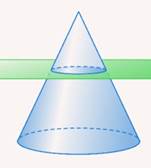
Рис. 5. Сечение, параллельное основанию конуса
Пусть дан конус. Проведем плоскость, параллельную плоскости основания этого конуса и пересекающую конус (см. рис. 5).
Она разобьет конус на два тела: одно из них – конус меньшего размера, а второе и называется усеченным конусом (см. рис. 6).
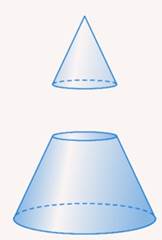
Рис. 6. Полученные тела при параллельном сечении
Таким образом, усеченный конус – это часть конуса, заключенная между его основанием и параллельной основанию плоскостью. Как и в случае с конусом, усеченный конус может иметь в основании круг – в этом случае его называют круговым. Если исходный конус был прямым, то и усеченный конус называют прямым. Как и в случае с конусами, мы будем рассматривать исключительно прямые круговые усеченные конусы, если специально не указано, что речь идет о непрямом усеченном конусе или в его основаниях не круги.
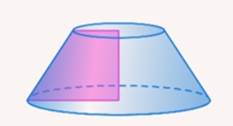
Рис. 7. Вращение прямоугольной трапеции
Наша глобальная тема – тела вращения. Усеченный конус – не исключение! Вспомним, что для получения конуса мы рассматривали прямоугольный треугольник и вращали его вокруг катета? Если полученный конус пересечь плоскостью, параллельной основанию, то от треугольника останется прямоугольная трапеция. Ее вращение вокруг меньшей боковой стороны и даст нам усеченный конус. Заметим снова, что речь, разумеется, идет только о прямом круговом конусе (см. рис. 7).
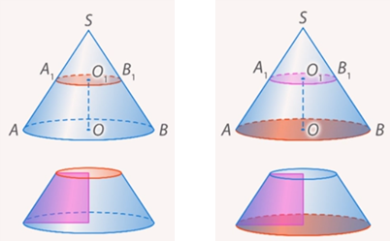
Рис. 8. Основания усеченного конуса
Сделаем несколько замечаний. Основание полного конуса и круг, получающийся в сечении конуса плоскостью, называют основаниями усеченного конуса (нижним и верхним) (см. рис. 8).
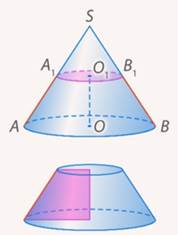
Рис. 9. Образующие усеченного конуса
Отрезки образующих полного конуса, заключенные между основаниями усеченного конуса, называют образующими усеченного конуса. Так как все образующие исходного конуса равны и все образующие отсеченного конуса равны, то и образующие усеченного конуса равны (не путать отсеченный и усеченный!). Отсюда и следует равнобедренность трапеции осевого сечения (см. рис. 9).
Отрезок оси вращения, заключенный внутри усеченного конуса, называют осью усеченного конуса. Этот отрезок, разумеется, соединяет центры его оснований (см. рис. 10).
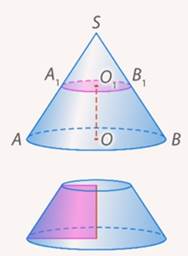
Рис. 10. Ось усеченного конуса
Высота усеченного конуса – это перпендикуляр, проведенный из точки одного из оснований к другому основанию. Чаще всего, в качестве высоты усеченного конуса рассматривают его ось.
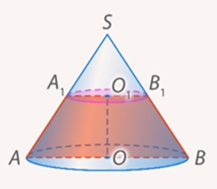
Рис. 11. Осевое сечение усеченного конуса
Осевое сечение усеченного конуса – это сечение, проходящее через его ось. Оно имеет вид трапеции, чуть позже мы докажем ее равнобедренность (см. рис. 11).
Площади боковой и полной поверхностей усеченного конуса
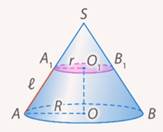
Рис. 12. Конус с введенными обозначениями
Найдем площадь боковой поверхности усеченного конуса. Пусть основания усеченного конуса имеют радиусы 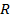 и и 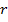 , а образующая равна , а образующая равна 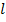 (см. рис. 12). (см. рис. 12).
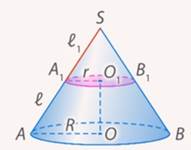
Рис. 13. Обозначение образующей отсеченного конуса
Найдем площадь боковой поверхности усеченного конуса как разность площадей боковых поверхностей исходного конуса и отсеченного. Для этого обозначим через 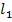 образующую отсеченного конуса (см. рис. 13). образующую отсеченного конуса (см. рис. 13).
Тогда искомая 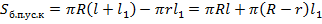 . .
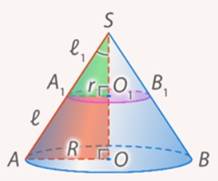
Рис. 14. Подобные треугольники
Осталось выразить 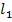 . .
Заметим, что из подобия треугольников 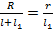 , откуда , откуда 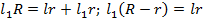 (см. рис. 14). (см. рис. 14).
Можно было бы выразить 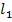 , разделив на разность радиусов, но нам это не нужно, ведь в искомом выражении как раз фигурирует произведение , разделив на разность радиусов, но нам это не нужно, ведь в искомом выражении как раз фигурирует произведение 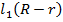 . Подставив вместо него . Подставив вместо него  , окончательно имеем: , окончательно имеем: 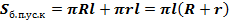 . .
Несложно теперь получить и формулу для площади полной поверхности. Для этого достаточно добавить площади двух кругов оснований: 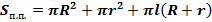 . .
|
Ссылка 1, 2
Презентация к уроку.
|
|
Закрепление.
Задача
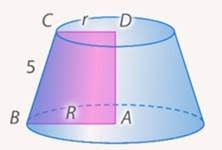
Рис. 15. Иллюстрация к задаче
Пусть усеченный конус получен вращением прямоугольной трапеции 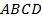 вокруг ее высоты вокруг ее высоты 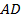 . Средняя линия трапеции . Средняя линия трапеции 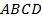 равна равна 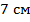 , а большая боковая стороны – , а большая боковая стороны – 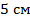 (см. рис. 15). Найти площадь боковой поверхности полученного усеченного конуса. (см. рис. 15). Найти площадь боковой поверхности полученного усеченного конуса.
Решение
По формуле мы знаем, что 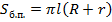 . .
Образующей конуса будет являться большая сторона исходной трапеции, то есть  Радиусы конуса – это основания трапеции. Найти их мы не можем. Но нам и не надо: нужна лишь их сумма, а сумма оснований трапеции вдвое больше ее средней линии, то есть она равна Радиусы конуса – это основания трапеции. Найти их мы не можем. Но нам и не надо: нужна лишь их сумма, а сумма оснований трапеции вдвое больше ее средней линии, то есть она равна 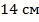 . Тогда . Тогда 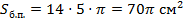 . .
Ответ: 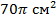 . .
|
Презентация
|
Конец урока
|
Рефлексия
|
Слайд
|
|
Домашнее задание:
Написать конспект.
Решить задачи.
|
Карточка-задание
|
5.Рефлексия по занятию
Рефлексия «+, -, интересно».
- Понравился ли вам урок?
- Что было трудным для вас?
- Что вам больше понравилось?
6. Домашнее задание
Оценочный лист:
№
|
Выполненное задание:
|
Баллы
|
|
Составить конспект.
|
30
|
|
Решить задачи.
|
70
|
Задачи:
Высота усеченного конуса равна 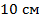 , а угол между образующей и плоскостью большего основания равен , а угол между образующей и плоскостью большего основания равен 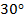 . Найдите образующую усеченного конуса. . Найдите образующую усеченного конуса.
Радиусы оснований усеченного конуса относятся как 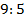 . Найдите площадь осевого сечения усеченного конуса, если его высота равна . Найдите площадь осевого сечения усеченного конуса, если его высота равна 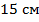 , а образующая – , а образующая – 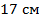 . .
Площади оснований усеченного конуса равны 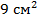 и и 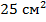 . Через середину его высоты проведено сечение, параллельное основаниям. Найдите площадь этого сечения. . Через середину его высоты проведено сечение, параллельное основаниям. Найдите площадь этого сечения.
Подпись преподавателя________________________
Скачано с www.znanio.ru
|
|
|
 Скачать 288.6 Kb.
Скачать 288.6 Kb.














