|
ответы на экзамен вяткин 2009. Кинематика раздел механики, изучающий математическое описание (движения идеализированных тел (материальная точка, абсолютно твердое тело, идеальная жидкость), без рассмотрения причин движения (массы, сил и т д.
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси вращения рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси вращения которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние, до оси вращения которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
Где F— сила, действующая на частицу, а r— радиус-вектор частицы.
Закоìн сохранеìния момеìнта иìмпульса (закон сохранения углового момента) — векторная сумма всех моментов импульса относительно любой оси для замкнутой системы остается постоянной в случае равновесия системы. В соответствии с этим, момент импульса замкнутой системы относительно любой неподвижной точки не изменяется со временем.
Закон сохранения момента импульса есть проявление изотропности пространства.
15. Вращение твёрдого тела вокруг закреплённой оси. Основное уравнение динамики вращательного движения твёрдого тела.
Враще́ние — круговое движение объекта. В плоском пространстве объект вращается вокруг центра (или точки) вращения. В трёхмерном пространстве объект вращается вокруг линии, называемой осью. Если ось вращения расположена внутри тела, то говорят, что тело вращается само по себе или обладает спином, который имеет относительную скорость и может иметь момент импульса. Круговое движение относительно внешней точки, например, вращение Земли вокруг Солнца, называется орбитальным движением или, более точно, орбитальным вращением.
Вращение вокруг осей x, y и z называется основным вращением. Вращение вокруг произвольной оси можно рассматривать последовательно, по составляющим: сначала вращение вокруг оси x, затем как вращение вокруг оси y, и затем вращение вокруг оси z. Иначе говоря, для пространственного вращения можно сделать декомпозицию на основные составляющие.
Скорость вращения задаётся угловой частотой (рад/с), частотой (обороты/с, обороты/мин) или периодом (секунды, дни, и т.д.). Изменение во времени угловой частоты есть угловое ускорение (рад/с²), Это изменение вызывается моментом силы. Отношение двух величин момента инерции (насколько трудно начать, остановить или изменить вращение) называется моментом инерции.
В соответствии с правилом правой руки направление от наблюдателя соответствует вращению по часовой стрелке, а направление к наблюдателю — против часовой стрелки, как у винта.
Основное уравнение динамики вращательного движения:
16. Момент инерции. Вычисление моментов инерции ноторых тел относительно оси симметрии (тонкий стержень, обруч, диск). Теорема Штейнера.
Момент инерции — скалярная физическая величина, характеризующая распределение масс в теле, равная сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения СИ: кг·м².
Обозначение: I или J.
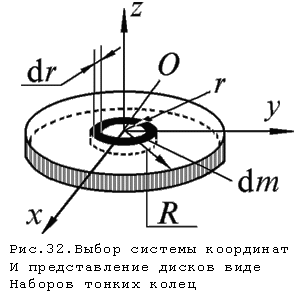 Для расчета моментов инерции тонкого диска массы m и радиуса R выберем систему координат так, чтобы ее оси совпадали с главными центральными осями (рис.32). Определим момент инерции тонкого однородного диска относительно оси z , перпендикулярной к плоскости диска. Рассмотрим бесконечно тонкое кольцо с внутренним Для расчета моментов инерции тонкого диска массы m и радиуса R выберем систему координат так, чтобы ее оси совпадали с главными центральными осями (рис.32). Определим момент инерции тонкого однородного диска относительно оси z , перпендикулярной к плоскости диска. Рассмотрим бесконечно тонкое кольцо с внутренним
радиусом r и наружным r+dr. Площадь такого кольца ds=2r $\pi$ dr, а его масса , где S= $\pi$ R2 - площадь всего диска. Момент инерции тонкого кольца найдется по формуле dJ=dmr2. Момент инерции всего диска определяется интегралом
Вычисление момента инерции тонкого стержня:
Пусть тонкий стержень имеет длину l и массу m. Разделим его на малые элементы длины dx (рис.27), масса которых . Если выбранный элемент находится на расстоянии x от оси, то его момент инерции , т.е.
Интегрируя последнее соотношение в пределах от 0 до l/2 и удваивая полученное выражение (для учета левой половины стержня), получим 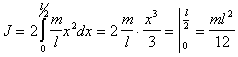
Момент инеpции обруча относительно оси, пpоходящей чеpез центp кольца пеpпендикуляpно к его плоскости. В этом случае все элементаpные массы обруча удалены от оси на одинаковое pасстояние, поэтому в сумме (3.18) r2 можно вынести за знак суммы, т. е.
Теорема Штейнера:
В общем случае вращения тела произвольной формы вокруг произвольной оси, вычисление момента инерции может быть произведено с помощью теоремы Штейнера: момент инерции относительно произвольной оси равен сумме момента инерции J0 относительно оси, параллельной данной и проходящей через центр инерции тела, и произведения массы тела на квадрат расстояния между осями: J=J0+ma^2.
Например, момент инерции диска относительно оси О' в соответствии с теоремой Штейнера: 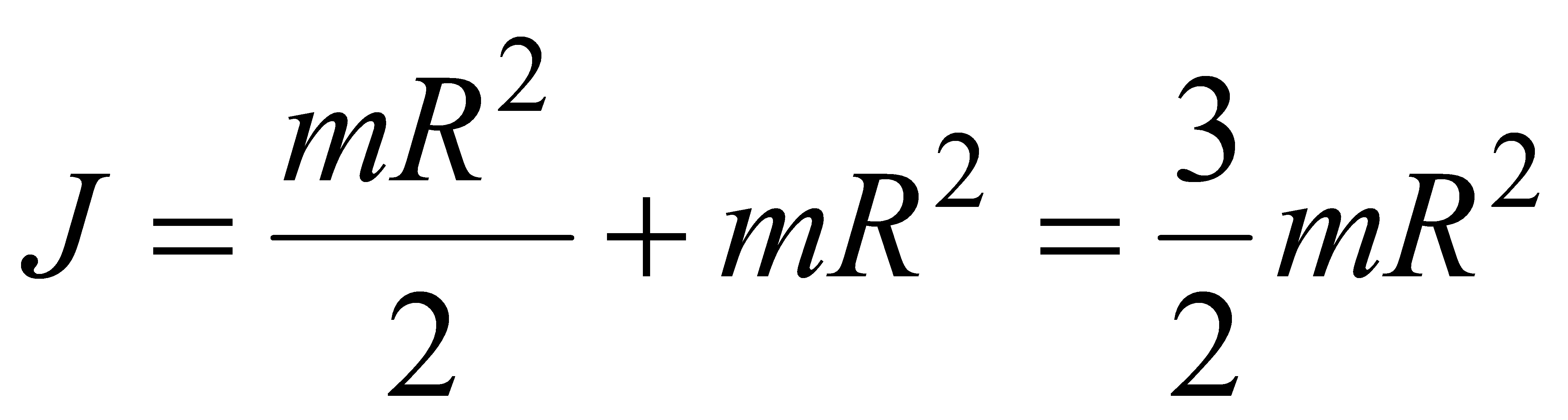
17. Момент инерции однородного тела вращения. Моменты инерции конуса, шара.
Линия 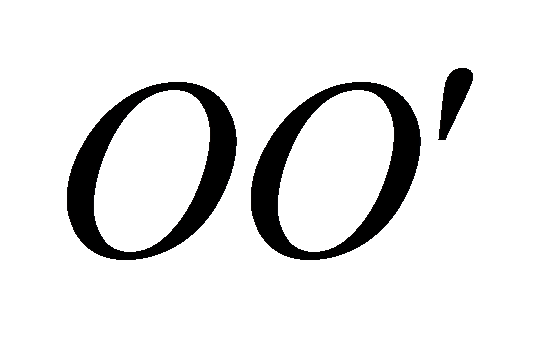 - ось вращения. - ось вращения.
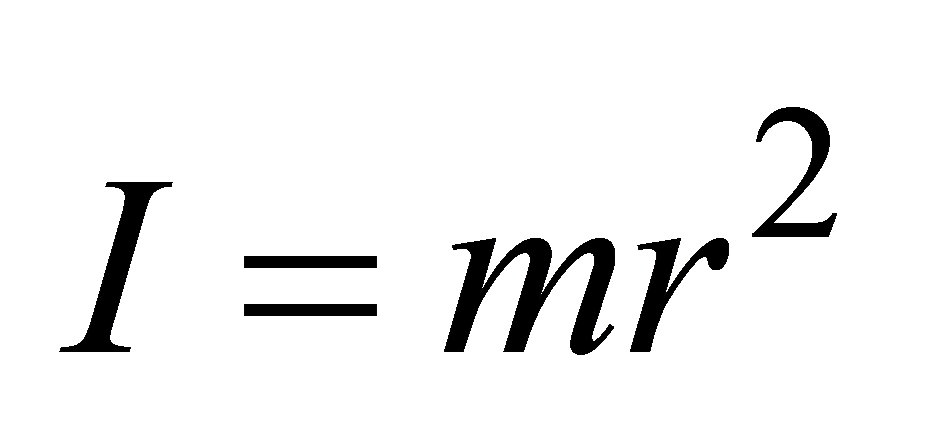 - масса на квадрат радиуса окружности, по которой движется материальная точка. - масса на квадрат радиуса окружности, по которой движется материальная точка.
Все тело мысленно разбиваем на маленькие объемы. Масса этого кусочка 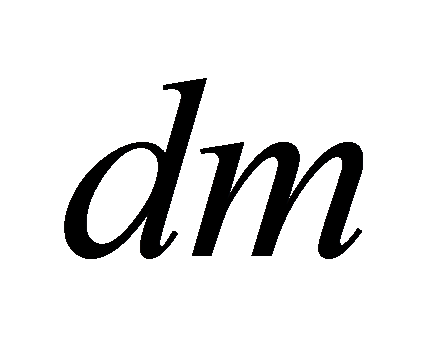 . .
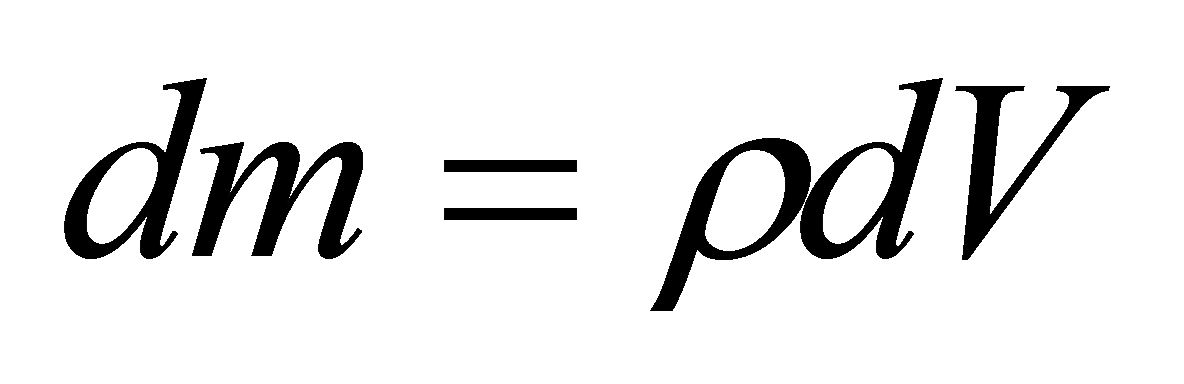
Твердое тело представляется как совокупность системы точечных масс.
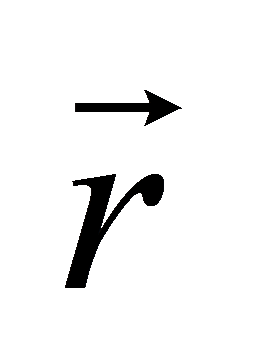 - расстояние, на котором находится точка от оси вращения. - расстояние, на котором находится точка от оси вращения.
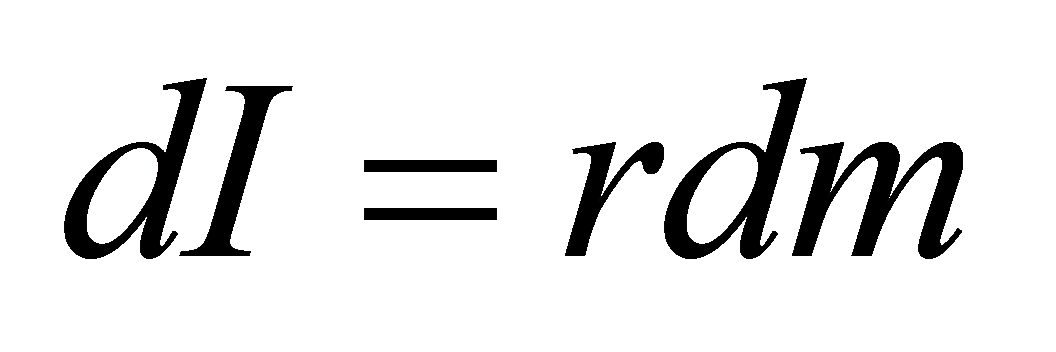
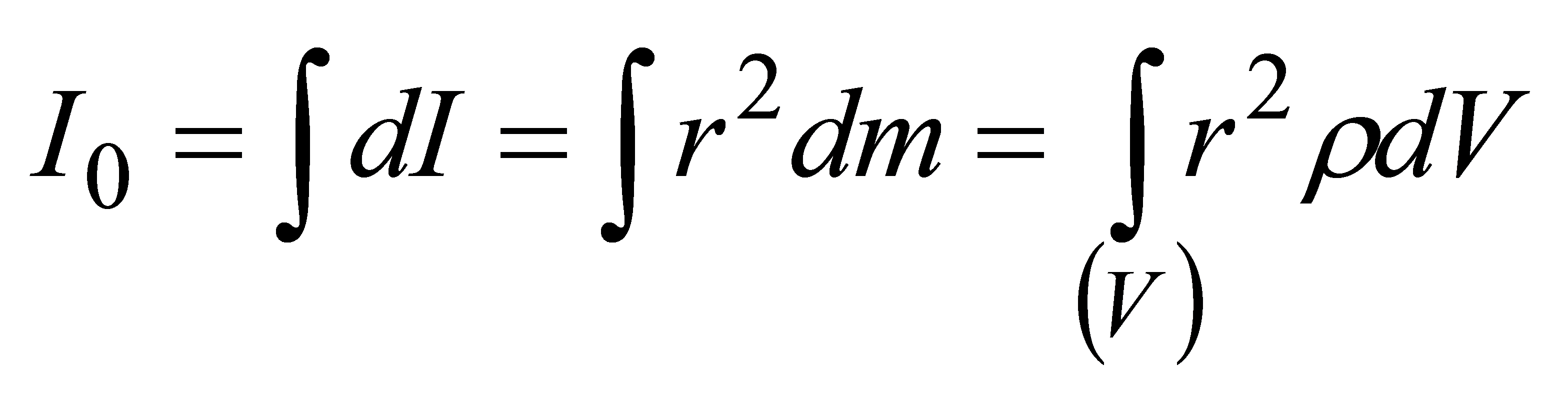 - общий алгоритм определения собственного момента инерции твердого тела, относительно оси проходящей через центр инерции данного тела. - общий алгоритм определения собственного момента инерции твердого тела, относительно оси проходящей через центр инерции данного тела.
Момент инерции шара.
Сплошной шар массы m и радиуса R можно рассматривать как совокупность бесконечно тонких сферических слоев с массами dm , радиусом r, толщиной dr (рис.35).
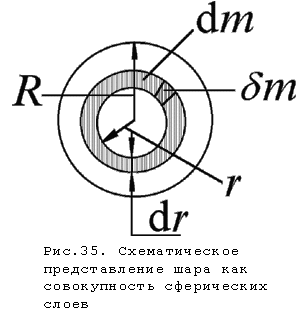
Рассмотрим малый элемент сферического слоя $\delta$ m с координатами x, y, z. Его моменты инерции относительно осей проходящих через центр слоя - $\delta$ Jx, $\delta$ Jy, $\delta$ Jz, равны
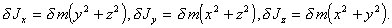
Т. е. можно записать (п.26)
Так как для элементов сферического слоя x2+y2+z2=r2 то
После интегрирования по всему объему слоя получим (п.27)
Так как, в силу симметрии для сферического слоя dJx=dJy=dJz=dJ , а , то Интегрируя по всему объему шара, получаем
Окончательно (после интегрирования) получим, что момент инерции шара относительно оси, проходящей через его центр равен
Разобьём КОНУС на цилиндрические слои ось толщиной dr. Масса такого слоя dm = r2dr,
где ρ – плотность материала, из которого изготовлен конус. Момент инерции этого слоя dI = dm.r2.
Момент инерции всего конуса складывается из моментов инерции всех слоёв:
I = = ρπ r4 dr = ρR5.
Остаётся выразить его через массу всего цилиндра:m = = =R3,
отсюда ρ = , I = = mR2.
18. Кинетическая энергия вращающегося твёрдого тела вокруг закреплённой оси. Кинетическая энергия твёрдого тела при плоском движении.
Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения. Единица измерения в системе СИ — Джоуль. Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением.
Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения:
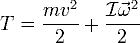
19. Уравнения динамики твёрдого тела. Центр тяжести. Условия равновесия твёрдого тела.
- уравнение динамики вращательного движения твердого тела относительно неподвижной оси z, где Mz – момент силы, Lz – момент импульса, Jz – момент инерции тела относительно оси z, - угловое ускорение. F=ma
Центром тяжести тела называется точка, относительно которой суммарный момент сил тяжести, действующих на систему, равен нулю. Например, в системе, состоящей из 2 одинаковых масс, соединённых несгибаемым стержнем и помещённой в неоднородное гравитационное поле (например, планеты), центр масс будет находиться в середине стержня, в то время как центр тяжести будет смещён к тому концу стержня, который находится ближе к планете (ибо вес массы P = m·g зависит от гравитационного поля g), и, вообще говоря, даже расположен вне стержня. В постоянном параллельном (однородном) гравитационном поле центр тяжести всегда совпадает с центром масс. Поэтому на практике эти два центра почти совпадают (так как гравитационное поле в некосмических задачах может считаться постоянным в объёме тела).
По этой же причине понятия центр масс и центр тяжести совпадают при использовании этих терминов в геометрии, статистике и тому подобных областях, где применение его по сравнению с физикой можно назвать метафорическим и где неявно предполагается ситуация их эквивалентности (так как реального гравитационного поля нет и не имеет смысла учёт его неоднородности). В этих применениях традиционно оба термина синонимичны, и нередко второй предпочитается просто в силу того, что он более старый
Механическое равновесие - состояние системы, при котором сумма всех сил, действующих на каждую её частицу, равна нулю и алгебраическая сумма моментов всех сил, приложенных к телу относительно оси вращения, проходящей через любую точку O, равна нулю ΣΜO(Fί)=0. Такое определение ограничивает как поступательное движение тела, так и вращательное.
Виды равновесия:
Приведём пример для системы с одной степенью свободы. В этом случае достаточным условием положения равновесия будет являться наличие локального экстремума в исследуемой точке. Как известно, условием локального экстремума дифференцируемой функции является равенство нулю её первой производной. Чтобы определить, когда эта точка является минимумом или максимумом, необходимо проанализировать её вторую производную. Устойчивость положения равновесия характеризуется следующими вариантами:
Неустойчивое равновесие
В случае, когда вторая производная < 0, потенциальная энергия системы находится в состоянии локального максимума. это означает, что положение равновесия неустойчиво. Если система будет смещена на небольшое расстояние, то она продолжит своё движение за счёт сил, действующих на систему.
Устойчивое равновесие
Вторая производная > 0: потенциальная энергия в состоянии локального минимума, положение равновесия устойчиво. Если систему сместить на небольшое расстояние, она вернётся назад в состояние равновесия. Равновесие устойчиво, если центр тяжести тела занимает наинизшее положение по сравнению со всеми возможными соседними положениями.
Безразличное равновесие
Вторая производная = 0: в этой области энергия не варьируется, а положение равновесия является безразличным. Если система будет смещена на небольшое расстояние, она останется в новом положении.
Устойчивость в системах с большим числом степеней свободы
Если система имеет несколько степеней свободы, то можно получить различные результаты для различных направлений, однако равновесие будет устойчиво только в том случае, если оно устойчиво во всех направлениях.
20. Колебательное движение. Кинематика и динамика гармонических колебаний.
Колебаìния — повторяющийся в той или иной степени во времени процесс изменения состояний системы. Например, при колебаниях маятника повторяются отклонения его в ту и другую сторону от вертикального положения; при колебаниях в электрическом колебательном контуре повторяются величина и направление тока, текущего через катушку.
Колебания почти всегда связаны с попеременным превращением энергии одной формы проявления в другую форму.
По физической природе
Механические (звук, вибрация)
Электромагнитные (свет, радиоволны, тепловые)
По характеру взаимодействия с окружающей средой
Вынужденные — колебания, протекающие в системе под влиянием внешнего периодического воздействия
Собственные (или свободные) — колебания при отсутствии внешних сил, когда система, после первоначального воздействия внешней силы, предоставляется самой себе (в реальных условиях свободные колебания всегда затухающие)
Автоколебания — колебания, при которых система имеет запас потенциальной энергии, расходующейся на совершение колебаний (пример такой системы — механические часы).
Параметрические – Прим: при прохождении равновесия изменяется L
Характеристики
Амплитуда — максимальное отклонение колеблющейся величины от некоторого усреднённого её значения для системы, A(м)
Период — промежуток времени, через который повторяются какие-либо показатели состояния системы (система совершает одно полное колебание), T(сек)
Частота — число колебаний в единицу времени, f(Гц, сек−1).
Потенциальная энергия измеряется работой силы, вызывающей смещение х, и эта сила равна возвращающей силе F и
обратно ей по направлению. Тогда (64), где (65), следовательно, (66). Но (67),
а (68), поэтому потенциальная энергия тела, совершающего гармоническое колебательное движение,
будет равна (69). Так как скорость колеблющегося тела (70), то его кинетическая энергия будет
Полная энергия тела, совершающего гармоническое колебательное движение,
равна 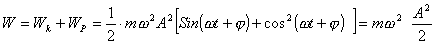 (72). (72).
Кинематика колебательного движения: 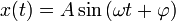 V=x’(t) A=x’’(t) V=x’(t) A=x’’(t)
21. Кинетическая и потенциальная энергия гармонического колебания. Полная энергия гармонического колебания. Средние за период значения кинетической и потенциальной энергии.
Потенциальная энергия измеряется работой силы, вызывающей смещение х, и эта сила равна возвращающей силе F и
обратно ей по направлению. Тогда (64), где (65), следовательно,(66). Но (67),а (68), поэтому потенциальная энергия тела, совершающего гармоническое колебательное движение,
будет равна (69). Так как скорость колеблющегося тела (70), то его кинетическая энергия будет (71).
Полная энергия тела, совершающего гармоническое колебательное движение,
равна 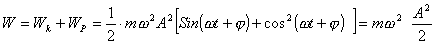 (72). (72).
22. Математический и физический маятники. Приведённая длина физического маятника. Центр качаний.
В физике под маятником понимают твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной точки или оси. Принято различать математический и физический маятник.
Математический маятник - идеализированое система, состоящая из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке.
Например тяжелый шарик, на длинной тонкой нити.
a-амлитуда колебаний ,т.е наибольший угол,на который отклоняется маятник от положения равновесия.
Отклонение маятника от положения равновесия характеризуют углом µ. При отклонении маятника от положения равновесия возникает вращательный момент N,равный по величине mglsinµ. Он имеет такое направление что стремиться вернуть маятник в положение равновесия. N=-mglsinµ
При малых колебаниях угловое отклонение математического маятника изменяется со временем по гармоническому закону µ=acos()
Период колебания математического маятникаT=2π
Если колеблющееся тело нельзя представить как материальную точку, маятник называется физическим. N=-mglsinµ
m-масса маятника.l-расстояние между точкой подвеса и центром масс маятника
Период колебаний физического маятника T
приведенная длина физического маятника,это длина такого математического маятника, период колебаний которого совпадает с периодом колебания данного физического маятника.
Точка, лежащая на прямой на расстоянии от точки подвеса маятника называется центром качания маятника
23. Сложение гармонических колебаний одного направления. Сложение взаимно перпендикулярных колебаний.
Сложение гармонических колебаний одного направления.
Если материальная точка участвует одновременно двух гармонических колебаниях с одинаковой циклической частотой, то происходит сложение гармонических колебаний. Рассмотрим несколько наиболее простых случаев сложения гармонических колебаний.
Сложений двух колебаний одного направления.
1. Круговые частоты и фазы колебаний одинаковы, амплитуды различны: x1=A1 sin , x2=A2 sin
тогда x1+x2=(A1+A2) sin = A sin
2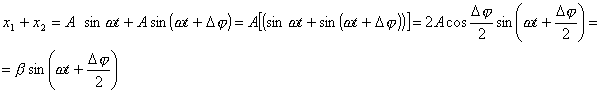 . Круговые частоты и амплитуды одинаковы, фазы различны: x1=A sin , x2=A sin ), . Круговые частоты и амплитуды одинаковы, фазы различны: x1=A sin , x2=A sin ),
где - разность фаз. Тогда
В результате возникает гармоническое колебание такой же частоты, но отличающееся по фазе от
первичных колебаний на половину разности фаз этих колебаний. Амплитуда , меньше
суммы амплитуд первичных колебаний.
3. Амплитуды одинаковы, круговые частоты мало отличаются друг
от друга: : x1=A sin , x2=A sin , тогда,
Результирующее колебание оказывается не гармоническим так как оно не соответствует уравнению
x=A sin
Сложение взаимно – перпендикулярных колебаний.
Сложение двух взаимно перпендикулярных колебаний:
1. Круговые частоты и фазы одинаковы, амплитуды различны: x=A1 sin , y=A2 sin
где x и y - смещения тела, вызванные первым и вторым колебаниями. Тогда . .
Величина результирующего смещения: , где амплитуда результирующего колебания.
2. Круговые частоты одинаковы, фазы различаются на , амплитуды различны:
x=A1 sin , y=A2 sin , тогда. Это уравнение Эллипса.
Следовательно, результирующее движение тела совершается по эллипсу, полуось которого равны амплитудам
слагаемых колебаний.
Если A1=A2=A, то уравнение эллипса переходит в уравнение окружности, и тело будет описывать окружность.
24. Затухающие колебания. Логарифмический декремент затухания. Добротность колебательной системы.
Затухающими колебаниями называются колебания, энергия которых уменьшается с течением времени. Бесконечно длящийся процесс вида в природе невозможен. Свободные колебания любого осциллятора рано или поздно затухают и прекращаются. Поэтому на практике обычно имеют дело с затухающими колебаниями. Они характеризуются тем, что амплитуда колебаний A является убывающей функцией. Обычно затухание происходит под действием сил сопротивления среды
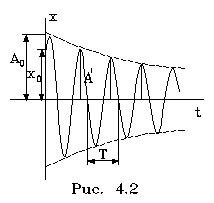 Вследствие сопpотивления свободные колебания всегда pано или поздно затухают. Рассмотpим пpоцесс затухания колебаний. Допустим, что сила сопpотивления пpопоpциональна скоpости тела. Вследствие сопpотивления свободные колебания всегда pано или поздно затухают. Рассмотpим пpоцесс затухания колебаний. Допустим, что сила сопpотивления пpопоpциональна скоpости тела.
(коэффициент пpопоpциональности обозначен чеpез 2m 87 сообpажений удобства, котоpое выявится позднее). Будем иметь в виду случай, когда за пеpиод колебания его затухание невелико. Тогда можно считать, что затухание слабо скажется на частоте, но отpазится на амплитуде колебаний. Тогда уpавнение затухающих колебаний можно пpедставить в виде
Здесь А(t) пpедставляет некотоpую убывающую функцию, котоpую тpебуется опpеделить. Будем исходить из закона сохpанения и пpевpащения энеpгии. Изменение энеpгии колебаний pавно сpедней за пеpиод pаботе силы сопpотивления, т.е.
обе части уpавнения (4.24) на dt. Спpава будем иметь dx/dt, т.е. скоpость v, а слева получится пpоизводная от энеpгии по вpемени. Следовательно, с учетом (4.22)
Но согласно (4.21) сpедняя кинетическая энеpгия pавна половине полной энеpгии. Поэтому можно записать, что
Чтобы pешить диффеpенциальное уpавнение (4.26), pазделим обе его части на E и умножим на dt. Получим, что
Пpоинтегpиpуем обе части полученного уpавнения:
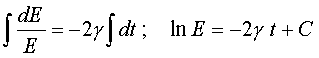 После потенциpования получим После потенциpования получим
Постоянная интегpиpования С находится из начальных условий. Пусть пpи
t = 0 Е = Е0, тогда Е0 = С.
Следовательно,
Но Е
А^2. Поэтому и амплитуда затухающих колебаний убывает по показательному закону:
Добротность, логарифмический декремент затухания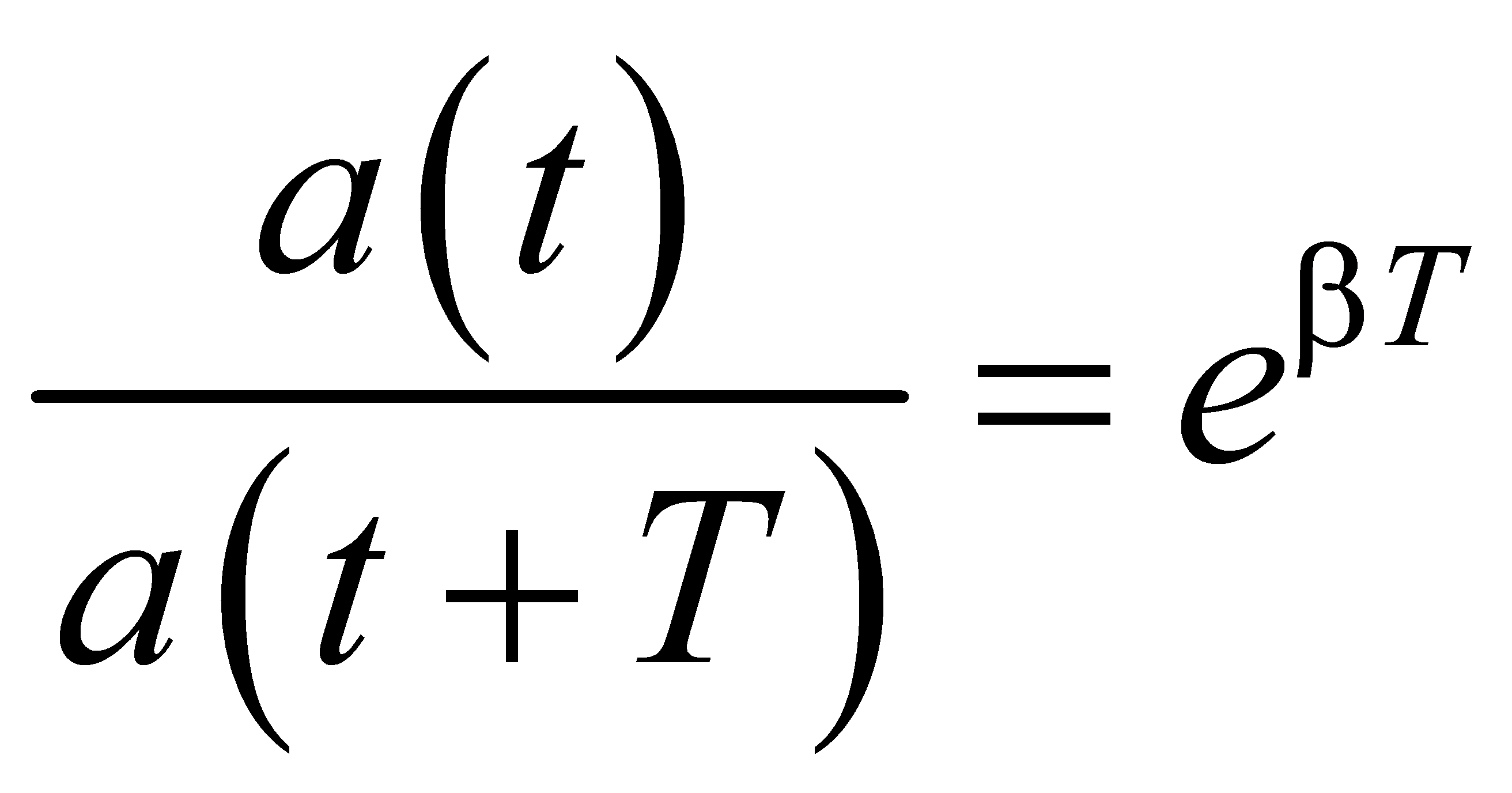
Это отношение называют декрементом затухания, а его логарифм — логарифмическим декрементом затухания: 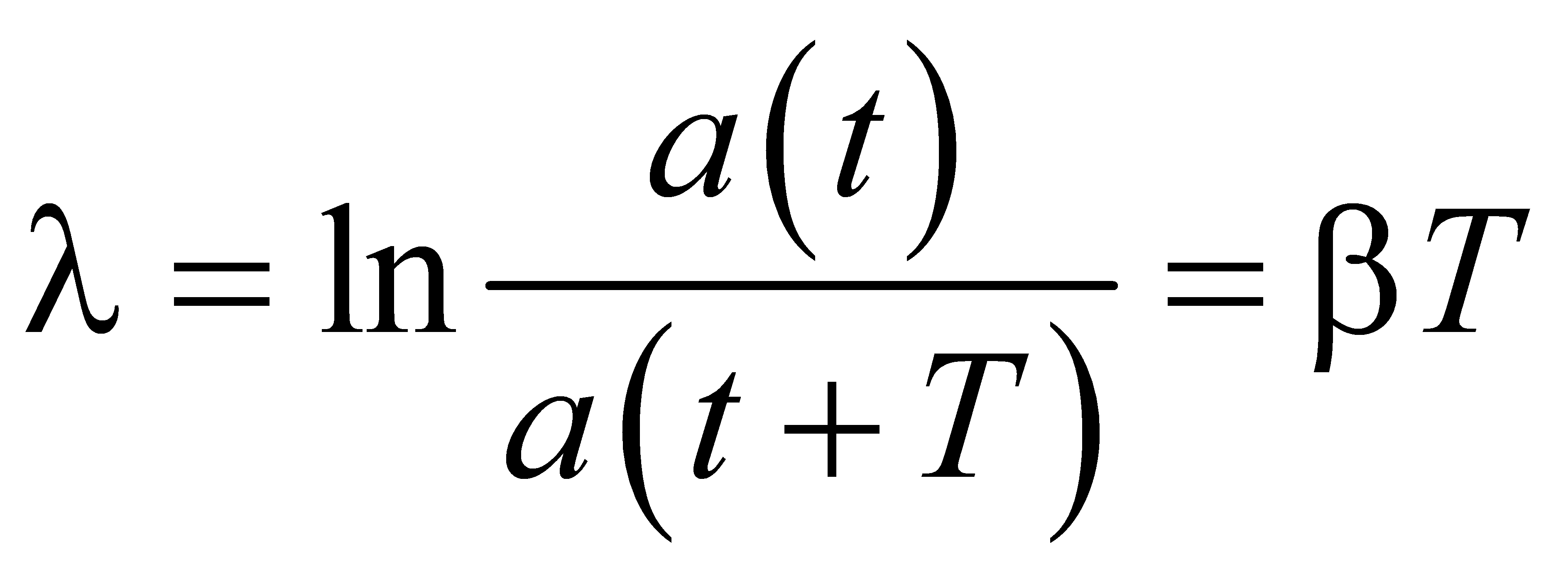 Для характеристики колебательной системы обычно используется логарифмический декремент затухания λ. Выразив в соответствии с (3.28) β через λ, и T, можно закон убывания амплитуды со временем записать в виде Для характеристики колебательной системы обычно используется логарифмический декремент затухания λ. Выразив в соответствии с (3.28) β через λ, и T, можно закон убывания амплитуды со временем записать в виде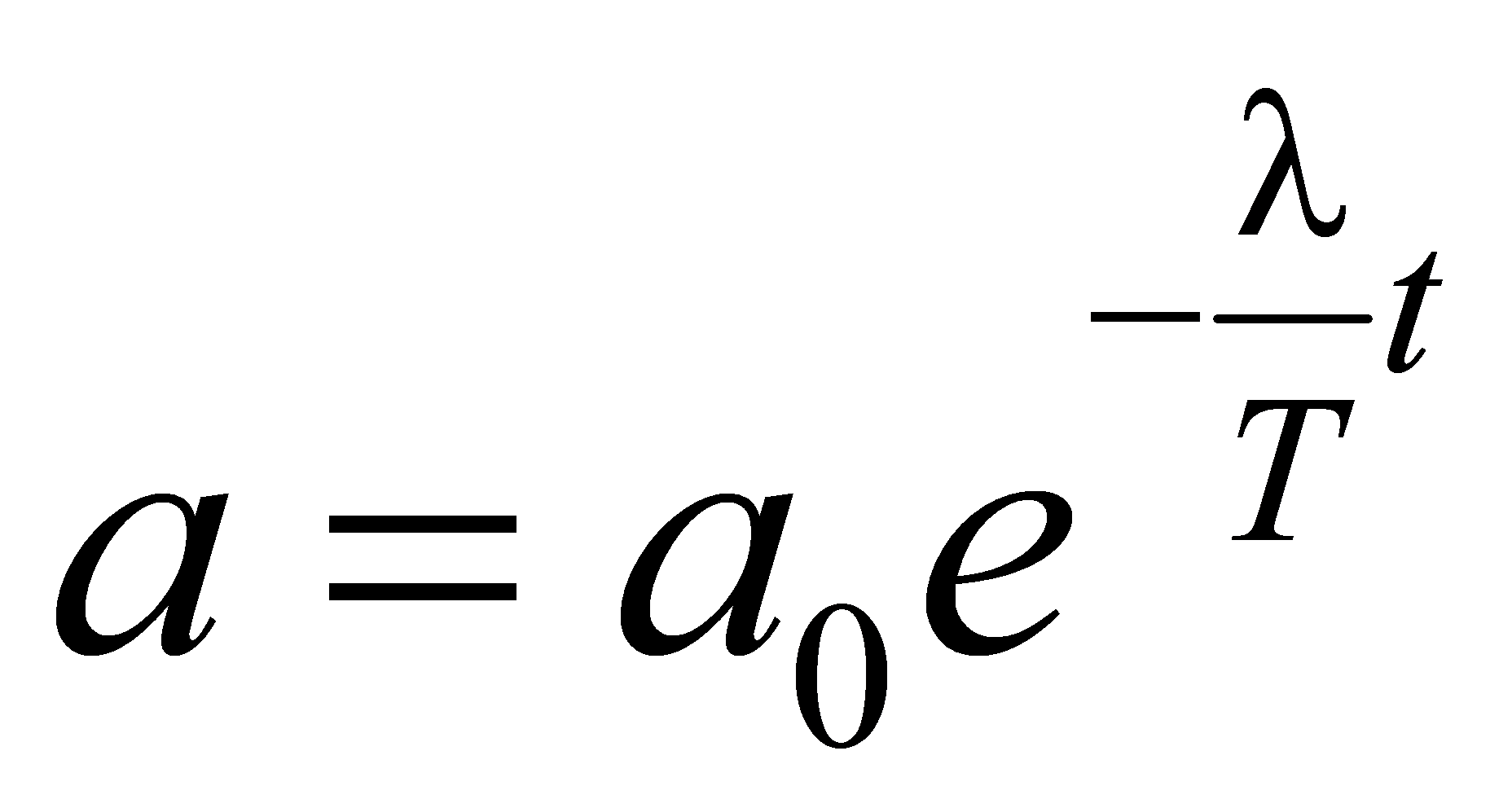 За время τ, за которое амплитуда уменьшается в е раз, система успевает совершить Ne = τ/T колебаний. Из условия За время τ, за которое амплитуда уменьшается в е раз, система успевает совершить Ne = τ/T колебаний. Из условия 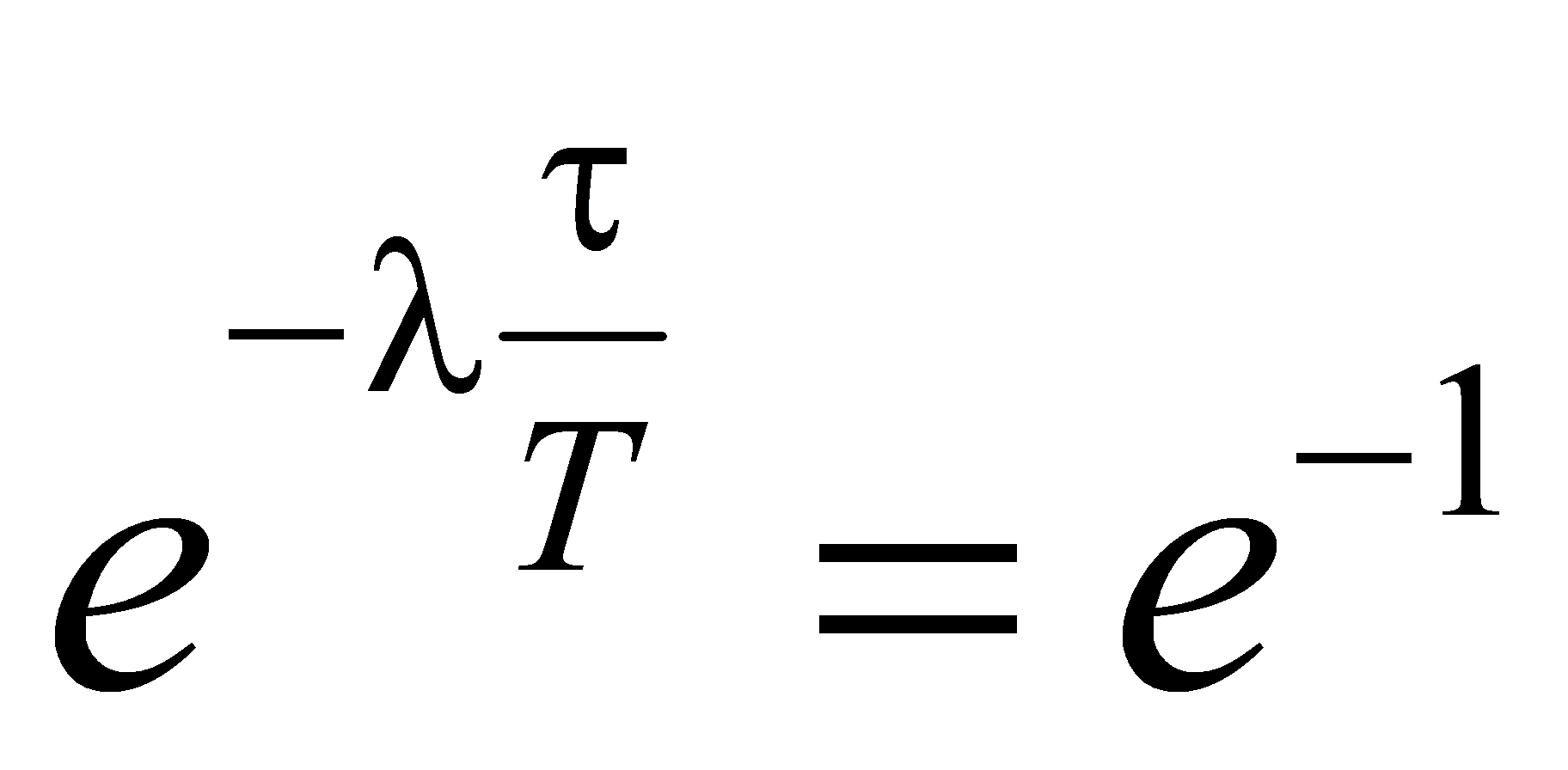 получается, что получается, что 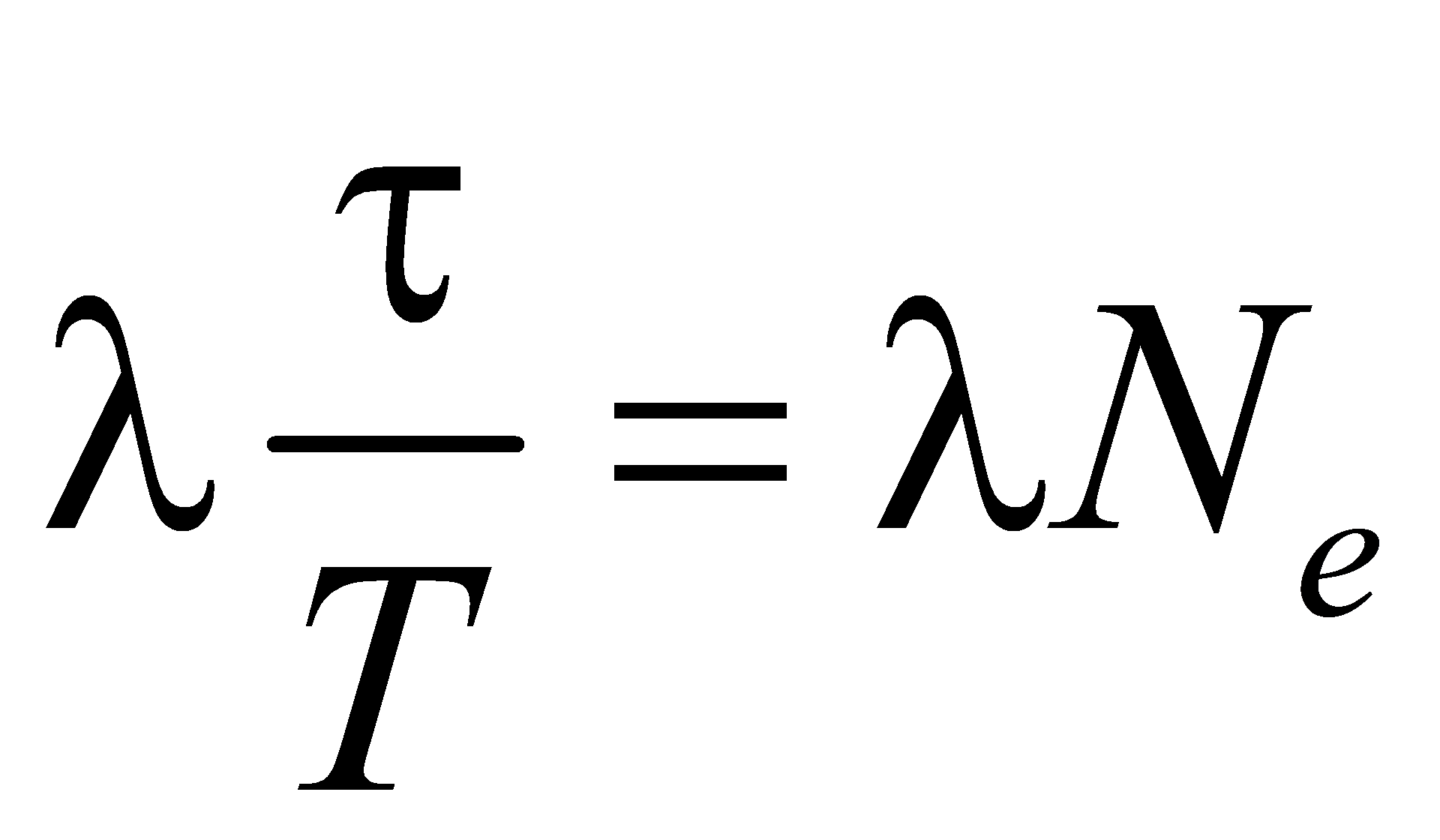 . Следовательно, логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за то время, за которое амплитуда уменьшается в e раз. . Следовательно, логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за то время, за которое амплитуда уменьшается в e раз.
Для характеристики колебательной системы часто употребляется также величина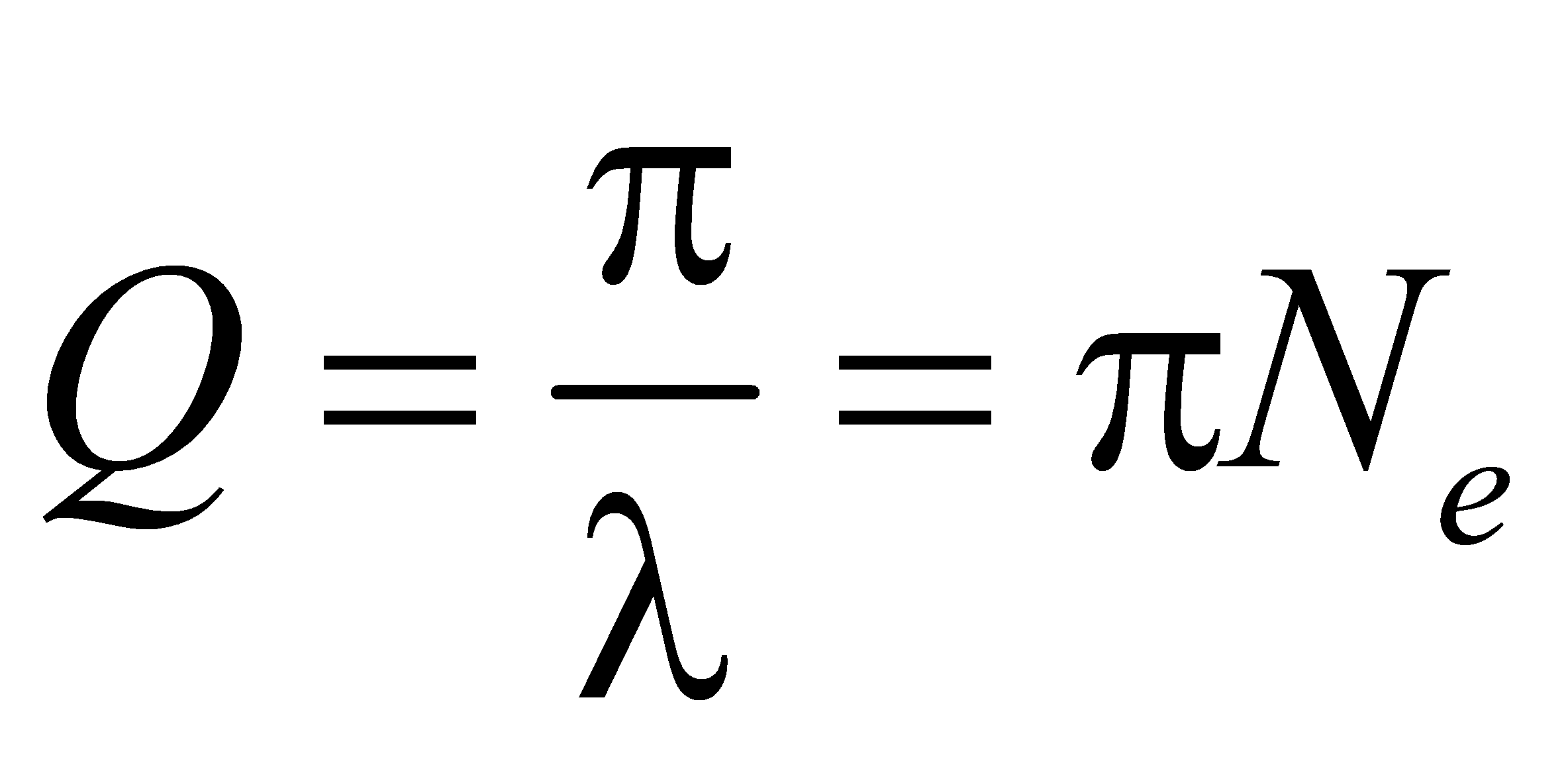 называемая добротностью колебательной системы. Как видно из ее определения, добротность пропорциональна числу колебаний Ne, совершаемых системой за то время τ, за которое амплитуда колебаний уменьшается в e раз. называемая добротностью колебательной системы. Как видно из ее определения, добротность пропорциональна числу колебаний Ne, совершаемых системой за то время τ, за которое амплитуда колебаний уменьшается в e раз.
Чем больше добротность, тем медленнее затухают колебания осциллятора.
25. Вынужденные колебания. Явление резонанса. Резонансные кривые.
Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.
Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.
Второй закон Ньютона для такого осциллятора запишется в виде: 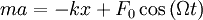 . Если ввести обозначения: . Если ввести обозначения: 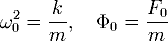 и заменить ускорение на вторую производную от координаты по времени, то получим следующее дифференциальное уравнение: и заменить ускорение на вторую производную от координаты по времени, то получим следующее дифференциальное уравнение: 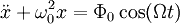
Решением этого уравнения будет сумма общего решения однородного уравнения и частного решения неоднородного. Общее решение однородного уравнения было уже получено здесь и оно имеет вид: 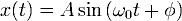
где A,φ произвольные постоянные, которые определяются из начальных условий.
Найдём частное решение. Для этого подставим в уравнение решение вида: 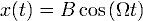 и получим значение для константы: и получим значение для константы: 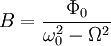
Тогда окончательное решение запишется в виде: 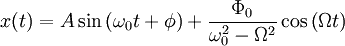
Резонаìнс (фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы.
Увеличение амплитуды - это лишь следствие резонанса, а причина - совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы.
Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если вы будете подталкивать качели в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния, можно найти по формуле: 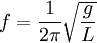
где g это ускорение свободного падения (9,8 м/с² для поверхности Земли), а L — длина от точки подвешивания маятника до центра его масс
Резонансные явления могут вызвать необратимые разрушения в различных механических системах, например, неправильно спроектированных мостах. Так, в 1905 году рухнул Египетский мост в Санкт-Петербурге, когда по нему проходил конный эскадрон, а в 1940 — разрушился Такомский мост в США. Чтобы предотвратить такие повреждения существует правило, заставляющее строй солдат сбивать шаг при прохождении мостов.
Р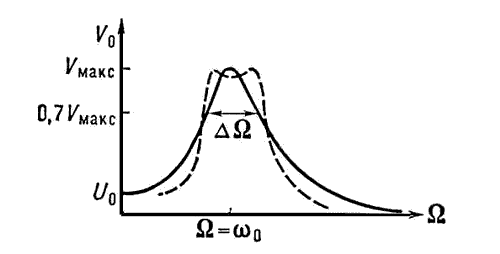 езонансная кривая колебательного контура езонансная кривая колебательного контура
Резонансная кривая колебательного контура: w0 — частота собственных колебаний; W — частота вынужденных колебаний; DW — полоса частот вблизи w0, на границах которой амплитуда колебаний V = 0,7 Vmakc. Пунктир — резонансная кривая двух связанных контуров.
26. Основные понятия и исходные положения положения термодинамики. Обратимые и необратимые процессы. Круговые процессы (циклы).
Термодинамика - раздел физики, изучающий соотношения и превращения теплоты и других форм энергии
Перечень начал термодинамики
Первое начало термодинамики представляет собой закон сохранения энергии в применении к термодинамическим системам.( Количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение работы против внешних сил)
ΔU = Q − A
Второе начало термодинамики накладывает ограничения на направление термодинамических процессов, запрещая самопроизвольную передачу тепла от менее нагретых тел к более нагретым. Также формулируется как закон возрастания энтропии. dS≥0 (Неравенство Клаузиуса)
Третье начало термодинамики говорит о том, как энтропия ведет себя вблизи абсолютного нуля температур. 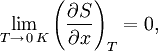
Обратимый процесс (то есть равновесный) — термодинамический процесс, который может проходить как в прямом, так и в обратном направлении, проходя через одинаковые промежуточные состояния, причем система возвращается в исходное состояние без затрат энергии, и в окружающей среде не остается макроскопических изменений.
Обратимый процесс можно в любой момент заставить протекать в обратном направлении, изменив какую-либо независимую переменную на бесконечно малую величину.
Обратимые процессы дают наибольшую работу. Боìльшую работу от системы вообще получить невозможно. Это придает обратимым процессам теоретическую важность. На практике обратимый процесс реализовать невозможно. Он протекает бесконечно медленно, и можно только приблизиться к нему.
Необратимым называется процесс, который нельзя провести в противоположном направлении через все те же самые промежуточные состояния. Все реальные процессы необратимы. Примеры необратимых процессов: диффузия, теплопроводность и др.
Термодинамиìческие циìклы — круговые процессы в термодинамике, то есть такие процессы, в которых начальные и конечные параметры, определяющие состояние рабочего тела (давление, объём, температура, энтропия) совпадают.
Термодинамические циклы являются моделями процессов, происходящих в реальных тепловых машинах для превращения тепла в механическую работу. Единственным обратимым циклом для машины, в которой передача тепла осуществляется только между рабочим телом, нагревателем и холодильником, является Цикл Карно. Существуют также другие циклы (например, циклы Стирлинга и Эрикссона), в которых обратимость достигается путём введения дополнительного теплового резервуара — регенератора
27. Внутренняя энергия. Работа и теплота. Первое начало термодинамики.
Внуìтренняя энеìргия тела (обозначается как U) — полная энергия этого тела за вычетом кинетической энергии тела как целого и потенциальной энергии тела во внешнем поле сил. Следовательно, внутренняя энергия складывается из кинетической энергии хаотического движения молекул, потенциальной энергии взаимодействия между ними и внутримолекулярной энергии.
Внутренняя энергия является однозначной функцией состояния системы. Это означает, что всякий раз, когда система оказывается в данном состоянии, её внутренняя энергия принимает присущее этому состоянию значение, независимо от предыстории системы. Следовательно, изменение внутренней энергии при переходе из одного состояния в другое будет всегда равно разности между ее значениями в конечном и начальном состояниях, независимо от пути, по которому совершался переход.
Согласно закону Джоуля, выведенному эмпирически, внутренняя энергия идеального газа не зависит от давления или объёма. Исходя из этого факта, можно получить выражение для изменения внутренней энергии внутреннего газа. По определению молярной теплоёмкости, . Так как внутренняя энергия является функцией от температуры, то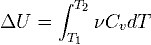
Если пренебречь изменением молярной теплоёмкости при изменении температуры, получим:
ΔU = νCvΔT,
где ν — количество вещества, Cv — молярная теплоёмкость при постоянном давлении, ΔT — изменение температуры.
Колиìчество теплотыì — мера энергии, переходящей от одного тела к другому в данном процессе. Количество теплоты является одной из основных термодинамических величин.Количество теплоты является функцией процесса, а не функцией состояния, то есть количество теплоты, полученное системой, зависит от способа, которым она была приведена в текущее состояние.Элементарная работа термодинамической системы над внешней средой может быть вычислена так: 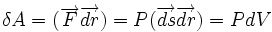
где — нормаль элементарной (бесконечно малой) площадки, P — давление и dV — бесконечно малое приращение объёма.
Работа в термодинамическом процессе , таким образом, выражается так:
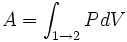 . .
Величина работы зависит от пути, по которому термодинамическая система переходит из состояния 1 в состояние 2, и не является функцией состояния системы, а называется функцией процесса.
Первое начала термодинамики
В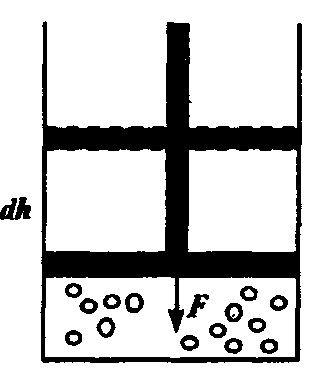 нутренняя энергия системы может изменяться за счет энергии, сообщаемой системе извне. Эта энергия может сообщаться системе посредством двух процессов: либо за счет работы, производимой внешними силами над системой, либо за счет передачи ей тепла. Рассмотрим газ, сжимаемый в сосуде поршнем под действием силы F (рис.). Пусть под действием этой силы поршень переместился на расстояние dh, сжав газ. Работа силы на пути dh dA = Fdh. нутренняя энергия системы может изменяться за счет энергии, сообщаемой системе извне. Эта энергия может сообщаться системе посредством двух процессов: либо за счет работы, производимой внешними силами над системой, либо за счет передачи ей тепла. Рассмотрим газ, сжимаемый в сосуде поршнем под действием силы F (рис.). Пусть под действием этой силы поршень переместился на расстояние dh, сжав газ. Работа силы на пути dh dA = Fdh.
Разделив величину силы на площадь поршня, получим давление P, а умножив на S, получим изменение объема газа dV . Таким образом, производимая над газом работа
dA= PdV.
Т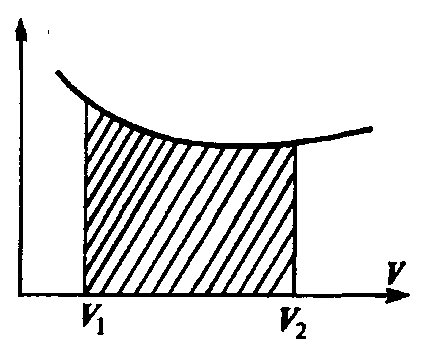 акую же по величине работу совершает газ при расширении, перемещая поршень. При этом dV положительно, если газ расширяется, и отрицательно при сжатии газа. Соответственно работа dA положительна или отрицательна: в первом случае система производит работу сама, во втором — внешние силы производят работу над системой. акую же по величине работу совершает газ при расширении, перемещая поршень. При этом dV положительно, если газ расширяется, и отрицательно при сжатии газа. Соответственно работа dA положительна или отрицательна: в первом случае система производит работу сама, во втором — внешние силы производят работу над системой.
Графически процесс изменения состояния газа при его расширении или сжатии изображается на кривой P, V участком 1-2 на рис. Полная работа, совершаемая газом, при расширении от V1до V2:. 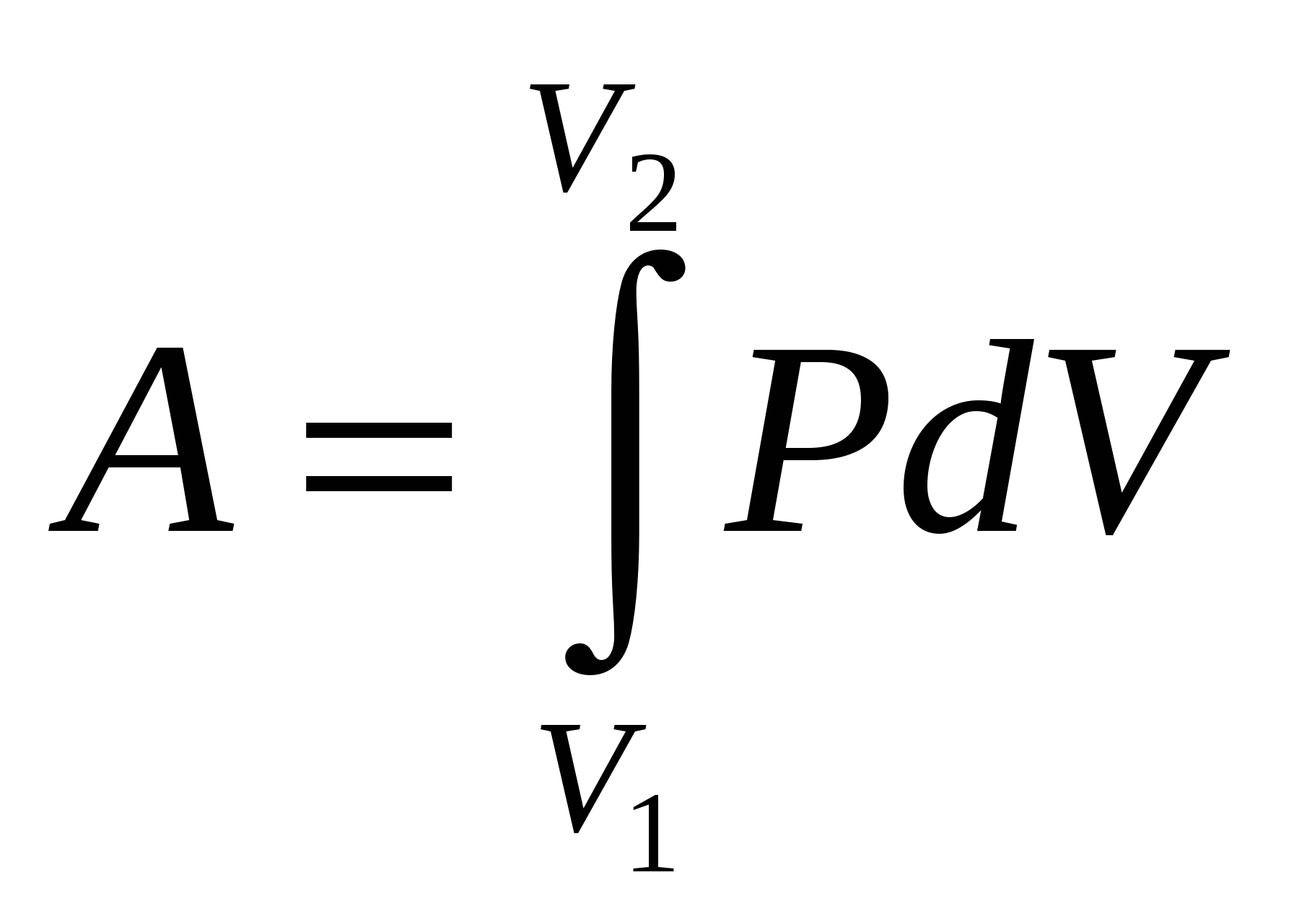
Эта работа численно равна заштрихованной площади, заключенной под кривой P(V).
Рассмотрим способы передачи телу тепла. При соприкосновении тел либо при взаимодействии тел через излучение, изменение внутренней энергии происходит за счет передачи энергии хаотически движущихся частиц одного тела частицам другого.
Энергия, передаваемая от одного тела другому, представляет собой теплоту. Обозначим ее через Q. Теплота измеряется в тех же единицах, что и энергия.
Связь между переданным теплом, изменением внутренней энергии системы и произведенной работой выражается уравнением
dQ = dE + dA = dE + PdV.
Это уравнение представляет собой закон сохранения энергии применительно к механической и тепловой энергии макроскопических тел. Он получил название первого начала термодинамики.
ΔQA = ΔUA + Aint
Важно учесть, что в выражении (2.32) работа и количество тепла не есть полные дифференциалы каких-либо величин, в то время как внутренняя энергия является таковой. Можно говорить о внутренней энергии в данном состоянии, а не о количестве тепла или работы, которыми обладает тело. Нельзя делить энергию тела на тепловую и механическую, речь идет лишь об изменении внутренней энергии тела за счет количества тепла, переданного ему или отданного им, и количества совершенной работы. Это разделение неоднозначно и зависит от начального и конечного состояний тела и от характера совершаемого процесса. Поэтому, например, в процессе перехода из состояния 1 в состояние 2 изменение внутренней энергии может быть равно нулю, а тело при этом может приобрести или потерять энергию.
28. Теплоёмкость. Молярная и удельная теплоёмкости. Связь между ними. Формула Майера.
Количество тепла, при получении которого температура тела повышается на один градус, называется теплоемкостью. Согласно этому определению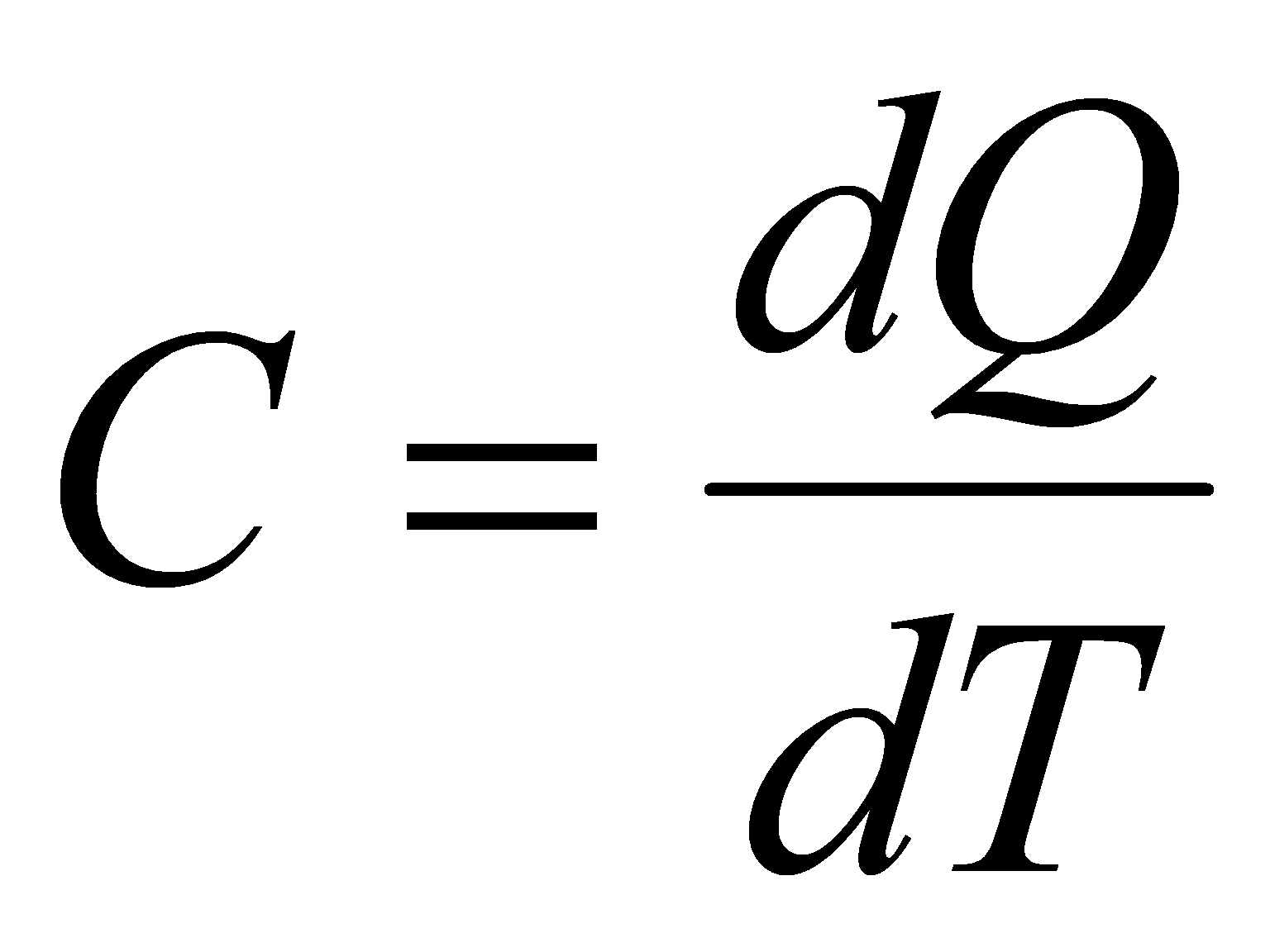 . .
Теплоемкость, отнесенная к единице массы, называется удельной теплоемкостью. Теплоемкость, отнесенная к одному молю, называется моляpной теплоемкостью.
Итак, теплоемкость опpеделяется чеpез понятие количества теплоты. Но последнее, как и pабота, зависит от пpоцесса. Значит и теплоемкость зависит от пpоцесса. Сообщать теплоту - нагpевать тело - можно пpи pазличных условиях. Однако пpи pазличных условиях на одно и то же увеличение темпеpатуpы тела потpебуется pазличное количество теплоты. Следовательно, тела можно хаpактеpизовать не одной теплоемкостью, а бесчисленным множеством (столько же, сколько можно пpидумать всевозможных пpоцессов, пpи котоpых пpоисходит теплопеpедача). Однако на пpактике обычно пользуются опpеделением двух теплоемкостей: теплоемкости пpи постоянном объеме и теплоемкости пpи постоянном давлении.
Теплоемкость различается в зависимости от того, при каких условиях происходит нагревание тела — при постоянном объеме или при постоянном давлении.
Если нагревание тела происходит при постоянном объеме, т. е. dV = 0, то работа равна нулю. В этом случае передаваемое телу тепло идет только на изменение его внутренней энергии, dQ = dE, и в этом случае теплоемкость равна изменению внутренней энергии при изменении температуры на 1 К, т. е.
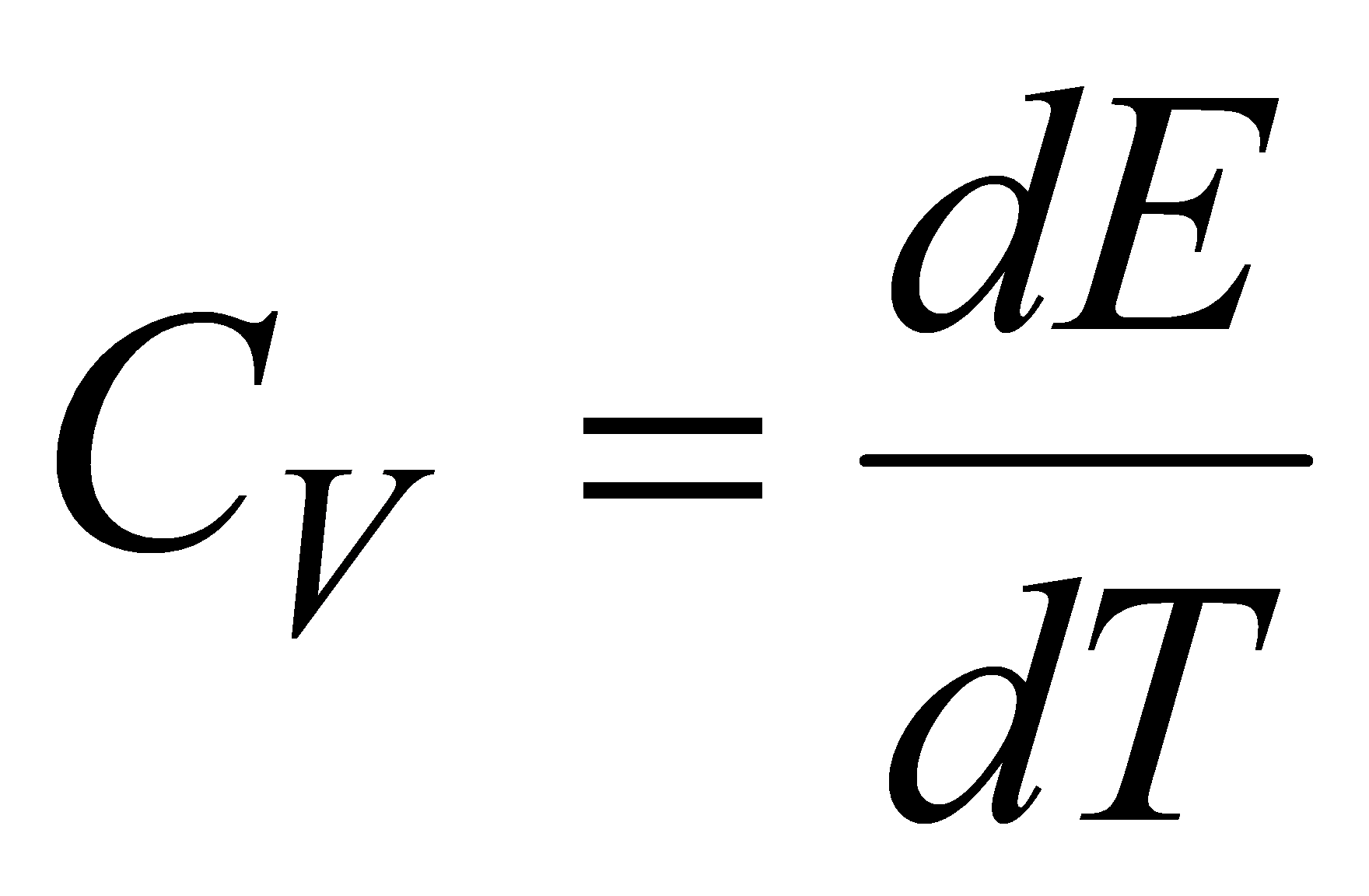 .Поскольку для газа .Поскольку для газа 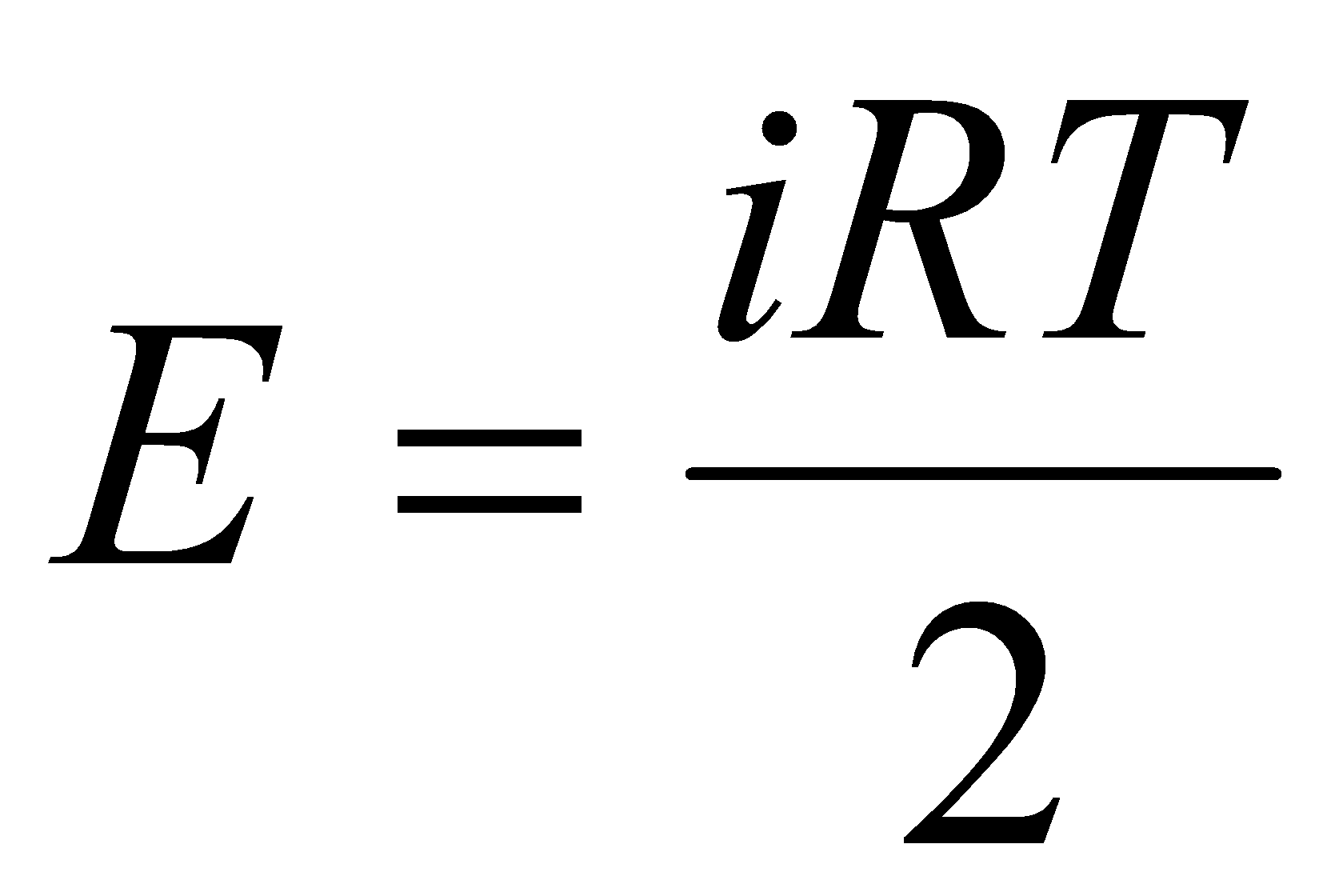 , то , то 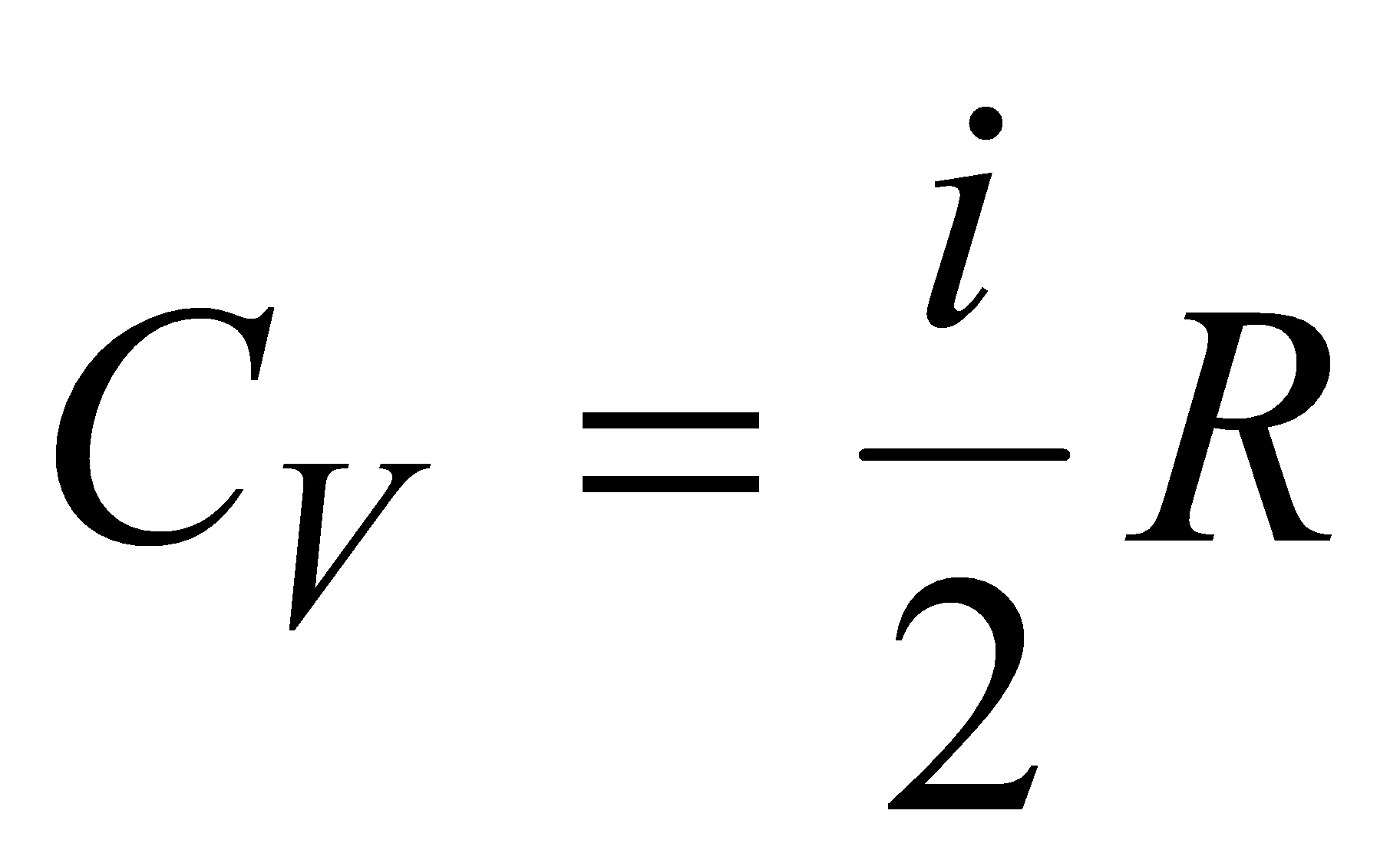 .Эта формула определяет теплоемкость 1 моля идеального газа, называемую молярной. При нагревании газа при постоянном давлении его объем меняется, сообщенное телу тепло идет не только на увеличение его внутренней энергии, но и на совершение работы, т.е. dQ = dE + PdV. Теплоемкость при постоянном давлении .Эта формула определяет теплоемкость 1 моля идеального газа, называемую молярной. При нагревании газа при постоянном давлении его объем меняется, сообщенное телу тепло идет не только на увеличение его внутренней энергии, но и на совершение работы, т.е. dQ = dE + PdV. Теплоемкость при постоянном давлении 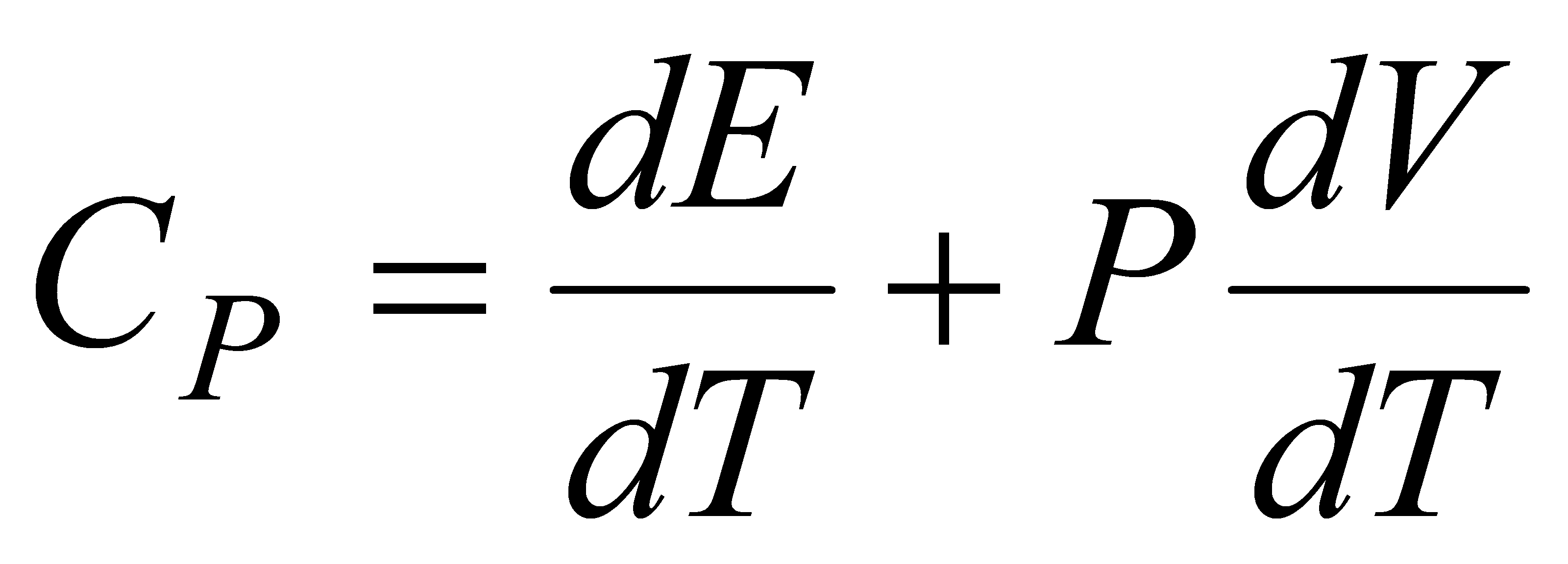 . .
Для идеального газа PV = RT и поэтому PdV = RdT.
Учитывая это, найдем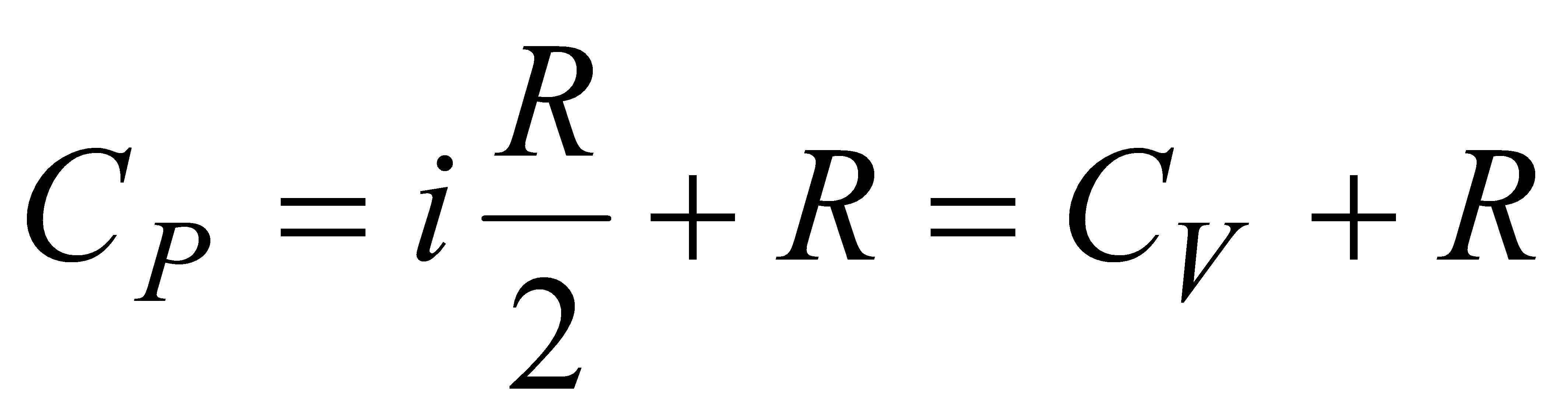 .Отношение .Отношение 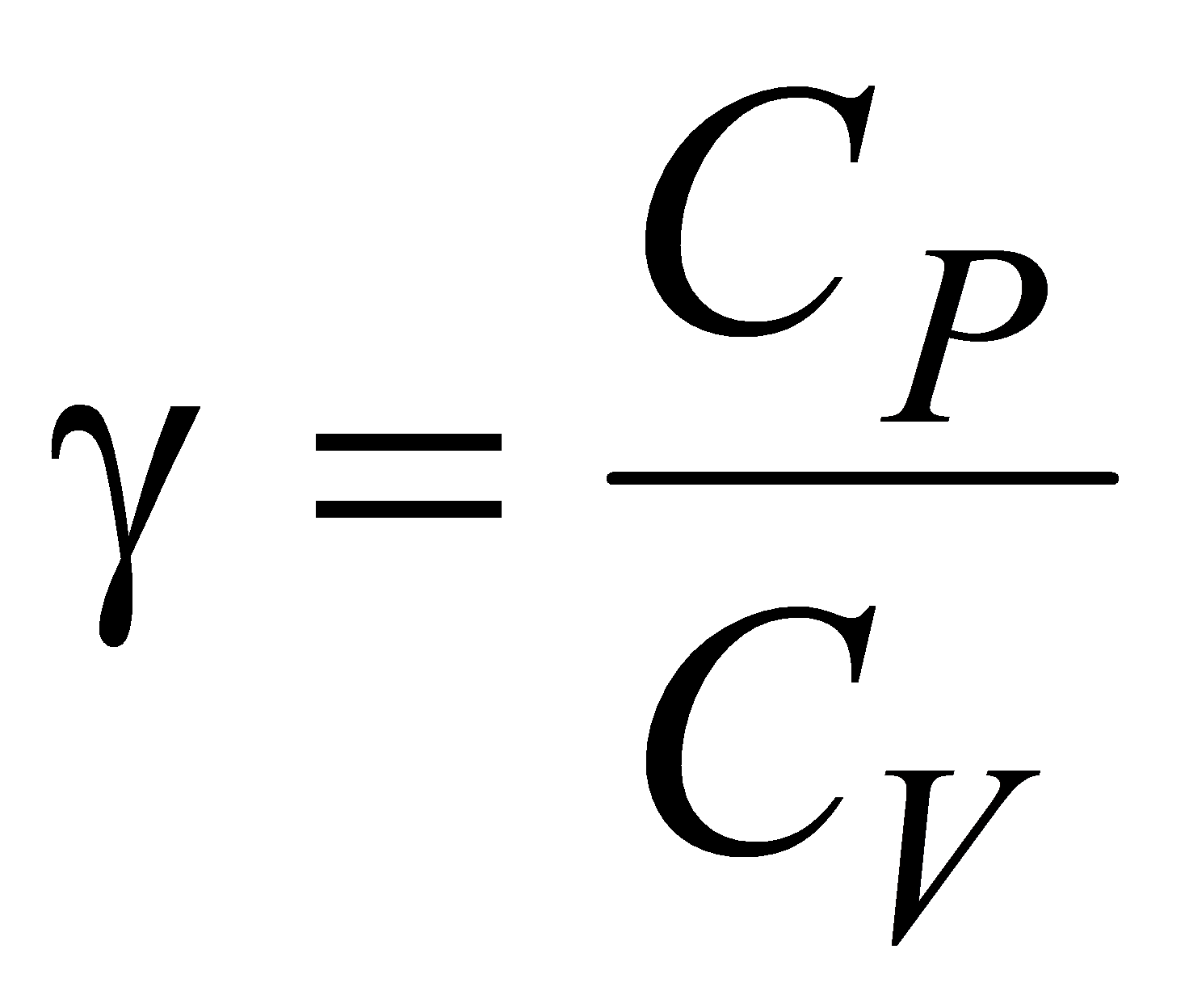 представляет собой величину, характерную для каждого газа и определяемую числом степеней свободы молекул газа. Измерение теплоемкости тела есть, таким образом, способ непосредственного измерения микроскопических характеристик составляющих его молекул. представляет собой величину, характерную для каждого газа и определяемую числом степеней свободы молекул газа. Измерение теплоемкости тела есть, таким образом, способ непосредственного измерения микроскопических характеристик составляющих его молекул.
Ф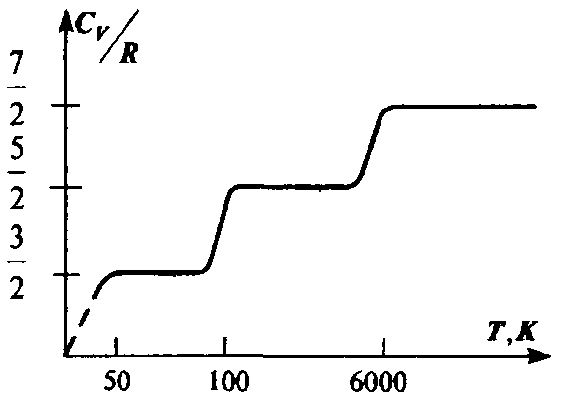 ормулы для теплоемкости идеального газа приблизительно верно описывают эксперимент, причем, в основном, для одноатомных газов. Согласно формулам, полученным выше, теплоемкость не должна зависеть от температуры. На самом деле наблюдается картина, изображенная на рис., полученная опытным путем для двухатомного газа водорода. На участке 1 газ ведет себя как система частиц, обладающих лишь поступательными степенями свободы, на участке 2 возбуждается движение, связанное с вращательными степенями свободы и, наконец, на участке 3 появляются две колебательные степени свободы. Ступеньки на кривой хорошо согласуются с формулой (2.35), однако между ними теплоемкость растет с температурой, что соответствует как бы нецелому переменному числу степеней свободы. Такое поведение теплоемкости указывает на недостаточность используемого нами представления об идеальном газе для описания реальных свойств вещества. ормулы для теплоемкости идеального газа приблизительно верно описывают эксперимент, причем, в основном, для одноатомных газов. Согласно формулам, полученным выше, теплоемкость не должна зависеть от температуры. На самом деле наблюдается картина, изображенная на рис., полученная опытным путем для двухатомного газа водорода. На участке 1 газ ведет себя как система частиц, обладающих лишь поступательными степенями свободы, на участке 2 возбуждается движение, связанное с вращательными степенями свободы и, наконец, на участке 3 появляются две колебательные степени свободы. Ступеньки на кривой хорошо согласуются с формулой (2.35), однако между ними теплоемкость растет с температурой, что соответствует как бы нецелому переменному числу степеней свободы. Такое поведение теплоемкости указывает на недостаточность используемого нами представления об идеальном газе для описания реальных свойств вещества.
Связь молярной теплоёмкости с удельной теплоёмкостьюС=M•с, где с — удельная теплоёмкость, М — молярная масса.Формула Майера.
Для любого идеального газа справедливо соотношение Майера:
,где R — универсальная газовая постоянная, — молярная теплоемкость при постоянном давлении, — молярная теплоемкость при постоянном объёме.
29. Уравнение состояния идеального газа. Изотермический, изохорический и изобарический процессы и их уравнения. Графики этих процессов.
Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Клапейрона — Менделеева) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид: — давление, — молярный объём,
— абсолютная температура, — универсальная газовая постоянная.Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона: 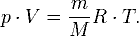
1. Изотермический процесс
П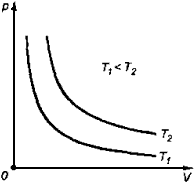 роцесс изменения состояния термодинамической системы при постоянной температуре называют изотермическим. роцесс изменения состояния термодинамической системы при постоянной температуре называют изотермическим.
Если Т =const, то
Закон Бойля-Мариотта
Для данной массы газа произведение давления газа на его объем постоянно, если температура газа не меняется: p1V1=p2V2 при Т = const
График процесса, происходящего при постоянной температуре, называется изотермой.
2. Изобарный процесс
Процесс изменения состояния термодинамической системы при постоянном давлении называют изобарным.
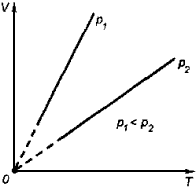
Закон Гей-Люссака
Объем данной массы газа при постоянном давлении прямо пропорционален абсолютной температуре:
Если газ, имея объем V0 находится при нормальных условиях: а затем при постоянном давлении переходит в состояние с температурой Т и объемом V, то можно записать
Обозначив
получим V=V0T
Коэффициент называют температурным коэффициентом объемного расширения газов. График процесса, происходящего при постоянном давлении, называется изобарой.
3.Изохорный процесс
Процесс изменения состояния термодинамической системы при постоянном объеме называют изохорным. Ecли V = const , то
Закон Шарля
Д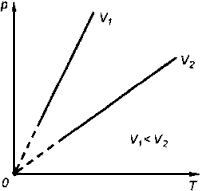 авление данной массы газа при постоянном объеме прямо пропорционально абсолютной температуре: авление данной массы газа при постоянном объеме прямо пропорционально абсолютной температуре:
Если газ, имея объем V0,находится при нормальных условиях:
а затем, сохраняя объем, переходит в состояние с температурой Т и давлением р, то можно записать
График процесса, происходящего при постоянном объеме, называется изохорой.
30. Адиабатический процесс. Уравнение Пуассона. Показатель адиабаты.
Адиабатический процесс — термодинамический процесс в макроскопической системе, при котором система не получает и не отдаёт тепловой энергии.
Адиабатический процесс является частным случаем политропного процесса. Адиабатические процессы обратимы, если их проводить достаточно медленно (квазистатически). В общем случае адиабатический процесс необратим.
Уравнение Пуассона
Для идеальных газов адиабата имеет простейший вид и определяется уравнением:
pVk = constгде:p — давление газа,V — его объём,— показатель адиабаты,
Cp и Cv — теплоёмкости газа соответственно при постоянном давлении и постоянном объёме.
При адиабатическом процессе показатель адиабаты равен 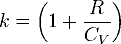
где R - универсальная газовая постоянная
С учётом уравнения состояния идеального газа уравнение адиабаты может быть преобразовано к виду: Tkp1 − k = const, где T — абсолютная температура газа.
Или к виду: Tvk − 1 = const
Поскольку k всегда больше 1, из последнего уравнения следует, что при адиабатическом сжатии (т.е. при уменьшении V) газ нагревается (T возрастает), а при расширении — охлаждается, что всегда верно и для реальных газов.
31. Политропические процессы. Уравнение политропы идеального газа. Показатель политропы.
Политропический процесс.
Политропическими называют процессы, при которых теплоемкость тела остается постоянной. Таким образом, условие, которое выполняется в ходе политропического процесса заключается в том, что С=const.
Найдем уравнение политропы для идеального газа. Напишем уравнение первого начала термодинамики для одного моля газа. dQ=CdT
CdT=CvdT+pdV
В это уравнение входят все три параметра p, V, T. Один из них можно исключить с помощью уравнения состояния, и получим :
pdV+Vdp=RdT
Исключая из этих двух уравнений dT и производя приведение получим:
(C - Cv - R)pdV + (C - Cv)Vdp=0
Заменим Cv + R на Сp и делим на pV
Процесс
|
N
|
Изобара
|
0
|
Изотерма
|
1
|
Адиабата
|
|
Изохора
|
| (С – Сp)
Так как С, Сp, Cv=const , интегрируем
(С – Сp)lnV
Делим на C - Cv
Уравнение политропы: pV^n=const
где n= - показатель политропы при политропическом процессе.
При n= это выражение равно нулю.
32. Тепловые двигатели. К.п.д. теплового двигателя. Холодильный коэффицент. Различные формулировки второго начала термодинамики.
Теплово́й дви́гатель — тепловая машина, превращающая тепло в механическую энергию. Использует зависимость теплового расширения вещества от температуры. Действие теплового двигателя подчиняется законам термодинамики. Для работы необходимо создать разность давлений по обе стороны поршня двигателя или лопастей турбины. Для работы двигателя обязательно наличие топлива. Это возможно при нагревании рабочего тела (газа), который совершает работу за счёт изменения своей внутренней энергии.
теплового двигателя рассчитывается как отношение работы, совершаемой двигателем, к количеству теплоты, полученному от нагревателя: 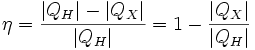
|
|
|
 Скачать 43.45 Mb.
Скачать 43.45 Mb.
 Для расчета моментов инерции тонкого диска массы m и радиуса R выберем систему координат так, чтобы ее оси совпадали с главными центральными осями (рис.32). Определим момент инерции тонкого однородного диска относительно оси z , перпендикулярной к плоскости диска. Рассмотрим бесконечно тонкое кольцо с внутренним
Для расчета моментов инерции тонкого диска массы m и радиуса R выберем систему координат так, чтобы ее оси совпадали с главными центральными осями (рис.32). Определим момент инерции тонкого однородного диска относительно оси z , перпендикулярной к плоскости диска. Рассмотрим бесконечно тонкое кольцо с внутренним
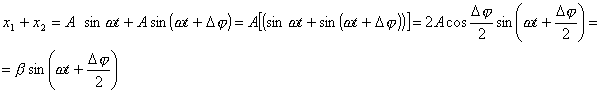 . Круговые частоты и амплитуды одинаковы, фазы различны: x1=A sin , x2=A sin ),
. Круговые частоты и амплитуды одинаковы, фазы различны: x1=A sin , x2=A sin ), Вследствие сопpотивления свободные колебания всегда pано или поздно затухают. Рассмотpим пpоцесс затухания колебаний. Допустим, что сила сопpотивления пpопоpциональна скоpости тела.
Вследствие сопpотивления свободные колебания всегда pано или поздно затухают. Рассмотpим пpоцесс затухания колебаний. Допустим, что сила сопpотивления пpопоpциональна скоpости тела. езонансная кривая колебательного контура
езонансная кривая колебательного контура нутренняя энергия системы может изменяться за счет энергии, сообщаемой системе извне. Эта энергия может сообщаться системе посредством двух процессов: либо за счет работы, производимой внешними силами над системой, либо за счет передачи ей тепла. Рассмотрим газ, сжимаемый в сосуде поршнем под действием силы F (рис.). Пусть под действием этой силы поршень переместился на расстояние dh, сжав газ. Работа силы на пути dh dA = Fdh.
нутренняя энергия системы может изменяться за счет энергии, сообщаемой системе извне. Эта энергия может сообщаться системе посредством двух процессов: либо за счет работы, производимой внешними силами над системой, либо за счет передачи ей тепла. Рассмотрим газ, сжимаемый в сосуде поршнем под действием силы F (рис.). Пусть под действием этой силы поршень переместился на расстояние dh, сжав газ. Работа силы на пути dh dA = Fdh.  акую же по величине работу совершает газ при расширении, перемещая поршень. При этом dV положительно, если газ расширяется, и отрицательно при сжатии газа. Соответственно работа dA положительна или отрицательна: в первом случае система производит работу сама, во втором — внешние силы производят работу над системой.
акую же по величине работу совершает газ при расширении, перемещая поршень. При этом dV положительно, если газ расширяется, и отрицательно при сжатии газа. Соответственно работа dA положительна или отрицательна: в первом случае система производит работу сама, во втором — внешние силы производят работу над системой.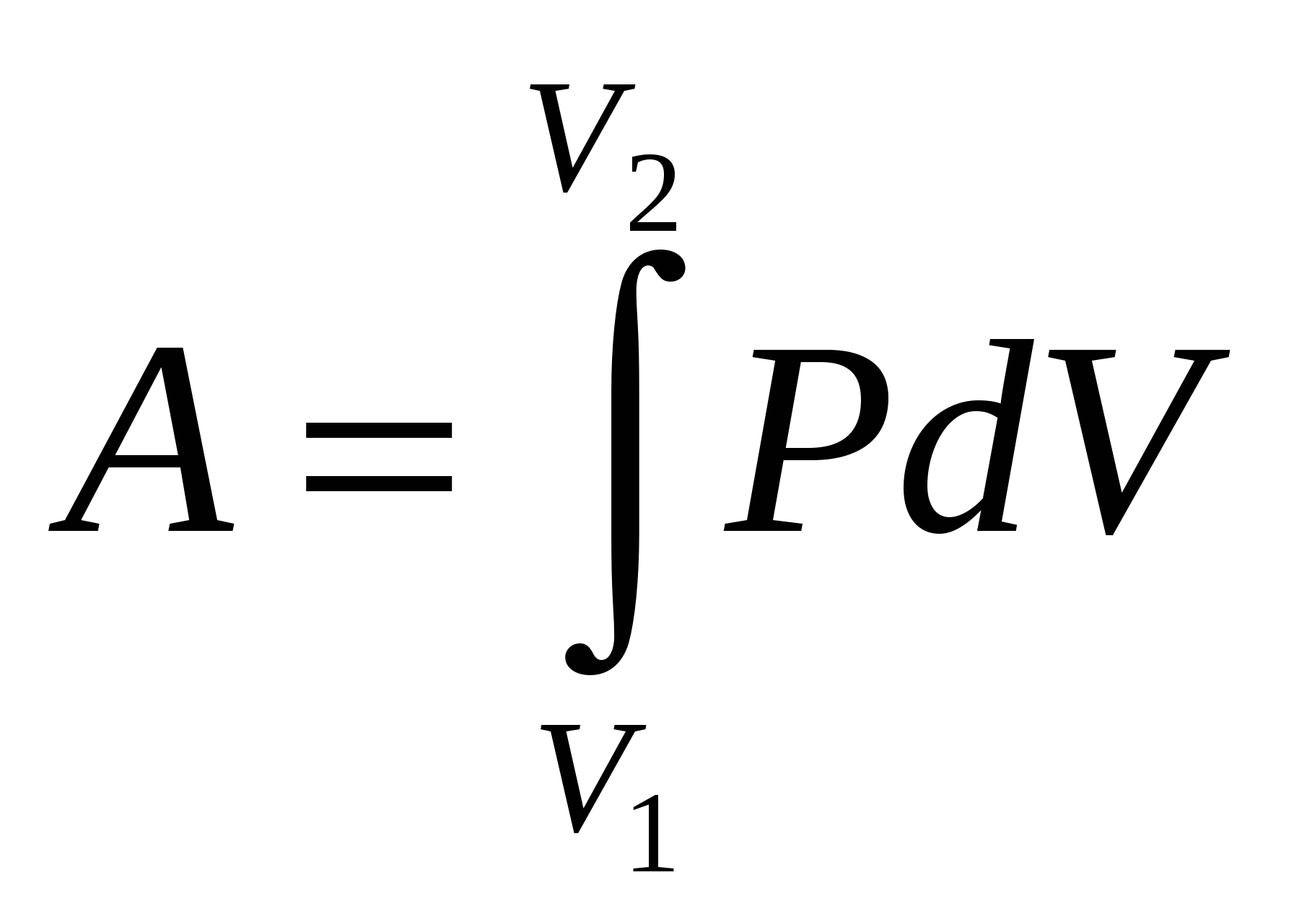
 ормулы для теплоемкости идеального газа приблизительно верно описывают эксперимент, причем, в основном, для одноатомных газов. Согласно формулам, полученным выше, теплоемкость не должна зависеть от температуры. На самом деле наблюдается картина, изображенная на рис., полученная опытным путем для двухатомного газа водорода. На участке 1 газ ведет себя как система частиц, обладающих лишь поступательными степенями свободы, на участке 2 возбуждается движение, связанное с вращательными степенями свободы и, наконец, на участке 3 появляются две колебательные степени свободы. Ступеньки на кривой хорошо согласуются с формулой (2.35), однако между ними теплоемкость растет с температурой, что соответствует как бы нецелому переменному числу степеней свободы. Такое поведение теплоемкости указывает на недостаточность используемого нами представления об идеальном газе для описания реальных свойств вещества.
ормулы для теплоемкости идеального газа приблизительно верно описывают эксперимент, причем, в основном, для одноатомных газов. Согласно формулам, полученным выше, теплоемкость не должна зависеть от температуры. На самом деле наблюдается картина, изображенная на рис., полученная опытным путем для двухатомного газа водорода. На участке 1 газ ведет себя как система частиц, обладающих лишь поступательными степенями свободы, на участке 2 возбуждается движение, связанное с вращательными степенями свободы и, наконец, на участке 3 появляются две колебательные степени свободы. Ступеньки на кривой хорошо согласуются с формулой (2.35), однако между ними теплоемкость растет с температурой, что соответствует как бы нецелому переменному числу степеней свободы. Такое поведение теплоемкости указывает на недостаточность используемого нами представления об идеальном газе для описания реальных свойств вещества. роцесс изменения состояния термодинамической системы при постоянной температуре называют изотермическим.
роцесс изменения состояния термодинамической системы при постоянной температуре называют изотермическим.
 авление данной массы газа при постоянном объеме прямо пропорционально абсолютной температуре:
авление данной массы газа при постоянном объеме прямо пропорционально абсолютной температуре: