ответы на экзамен вяткин 2009. Кинематика раздел механики, изучающий математическое описание (движения идеализированных тел (материальная точка, абсолютно твердое тело, идеальная жидкость), без рассмотрения причин движения (массы, сил и т д.
 Скачать 43.45 Mb.
|
|
7. Импульс. Импульс силы. Закон сохранения импульса. Центр масс. Импульс.  . Выражение представляет собой уравнение движения частицы. Если его проинтегрировать, то можно найти траекторию частицы r = r(t, F). Однако часто это не является необходимым. Оказывается, уравнения Ньютона обладают тем свойством, что некоторые величины, характеризующие движение частицы, остаются неизменными во все время движения. О таких величинах принято говорить, что они сохраняются. Их также называют интегралами движения. Знание интегралов движения позволяет получить ряд важных следствий без фактического решения уравнений движения. Получим некоторые сохраняющиеся величины. Перепишем в виде  Величина  называется импульсом тела. Внеся величину m под знак дифференциала в (1.26), закон Ньютона можно записать в форме:  Физический смысл импульса становится очевидным, если уравнение проинтегрировать на конечном интервале времени от 0 до t :  Изменение импульса служит мерой величины силы, действующей на тело в течение конечного промежутка времени. Численно величина импульса . Импульс силы — это векторная физическая величина, равная произведению силы на время ее действия, мера воздействия силы на тело за данный промежуток времени (в поступательном движении). За конечный промежуток времени эта величина равна определённому интегралу от элементарного импульса силы, где пределами интегрирования являются моменты начала и конца промежутка времени действия силы. В случае одновременного действия нескольких сил сумма их импульсов равна импульсу их равнодействующей за то же время.  Закон сохранения импульса. Рассмотрим тело или систему тел в отсутствие внешних сил. Система тел, на которую не действуют внешние силы (или векторная сумма этих сил равна нулю), является замкнутой. В этом случае F=0; как видно из уравнений или . ,  , т.е. величина , остается постоянной во все время движения. Полученный результат представляет собой закон сохранения импульса, который имеет место как для одного тела, так и для системы тел в отсутствие внешних сил. Ц 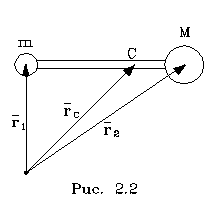 ентр масс.Введем в pассмотpение некую сpеднюю по массе точку системы, называемую центpом масс (или центpом инеpции). Пpежде чем записать общую фоpмулу, опpеделяющую центp масс системы, пpиведем пpостой пpимеp. Найдем центp масс несимметpичной гантели (тяжелый и легкий шаpы), у котоpой масса пеpемычки ничтожно мала. Центp масс каждого шаpа лежит в его геометpическом центpе. Радиус-вектоp центpа масс всей гантели находится по фоpмуле Поместим начало кооpдинат в центp масс гантели. Тогда rc=0, а значит, mr1 = -Mr2;откуда следует, что r1/r2 = M/m. Следовательно, центp масс несимметpичной гантели делит pасстояние между центpами шаpов на отpезки, обpатно пропоpциональные массам шаpов. 8. Механическая работа. Мощность. Энергия. Кинетическая энергия. Механическая работа— это физическая величина, являющаяся количественной характеристикой действия силы F на процесс γ(t), зависящая от численной величины и направления силы и от перемещения точки ее приложения При прямолинейном движении и постоянном значении силы работа равна произведению величины проекции вектора силы на направление движения и величины пройденного пути: При этом действующая сила F и вектор скорости v процесса γ за всё время наблюдения Δt постоянны, работа численно равна , в противном случае она вычисляется как интеграл:  Как следствие, если движение процесса ортогонально силе F, её работа равна нулю. В термодинамике работа, совершенная газом (работа совершенная над газом), рассчитывается как интеграл давления по объему:  Мощность — физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.
Если на движущееся тело действует сила, то эта сила совершает работу. Мощность в этом случае равна скалярному произведению вектора силы на вектор скорости, с которой движется тело: P=F*V=F*V*cos(alpha) Частный случай мощности при вращательном движении:
Энеìргия — скалярная физическая величина, Механическая работа являющаяся единой мерой различных форм движения материи и мерой перехода движения материи из одних форм в другие. Основное утверждение про энергию носит название закон сохранения энергии и заключается в том, что суммарная энергия замкнутой системы не изменяется во времени. Механика различает потенциальную энергию (или, в более общем случае, энергия взаимодействия тел) и кинетическую энергию. Их сумма называется полной энергией. Термодинамика рассматривает внутреннюю энергию и иные термодинамические потенциалы. Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением. Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения:  Соотношение кинетической и внутренней энергии Кинетическая энергия зависит от того, с каких позиций рассматривается система. Если рассматривать макроскопический объект (например, твёрдое тело видимых размеров), то тело неподвижно как единое целое, и такие формы энергии, как тепло, рассматриваются как внутренняя энергия. Кинетическая энергия в этом случае появляется лишь тогда, когда тело движется как целое. То же тело, рассматриваемое с микроскопической точки зрения, состоит из атомов, молекул, и внутренняя тепловая энергия обусловлена движением атомов и молекул и рассматривается как следствие броуновского движения, а температура тела отличается от кинетической энергии такого движения лишь на постоянный коэффициент — постоянную Больцмана. 9. Поле сил. Консервативные силы. Потенциальная энергия. Связь между потенциальной энергией и силой. Полем сил называют область пространства, в каждой точке которого на помещенную туда частицу действует сила, закономерно меняющаяся от точки к точке. Примером может служить поле силы тяжести Земли или поле сил сопротивления в потоке жидкости (газа). Если сила в каждой точке силового поля не зависит от времени, то такое поле называют стационарным. Ясно, что силовое поле, стационарное в одной системе отсчета, в другой системе может оказаться и нестационарным. В стационарном силовом поле сила зависит только от положения частицы. В физике консерватиìвные сиìлы (потенциальные силы) — силы, работа которых не зависит от формы траектории (зависит только от начальной и конечной точки приложения сил). Отсюда следует следующее определение: консервативные силы — такие силы, работа по любой замкнутой траектории которых равна 0. Если в системе действуют только консервативные силы, то механическая энергия системы сохраняется. В школьной программе по физике силы разделяют на консервативные и неконсервативные. Примерами консервативных сил являются: сила тяжести, сила упругости. Примерами неконсервативных сил являются сила трения и сила сопротивления. Потенциальная энергия — работа, которую необходимо совершить, чтобы перенести тело из некой точки отсчёта в данную точку в поле консервативных сил. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы Также потенциальная энергия является характеристикой взаимодействия нескольких тел или тела и поля. Любая физическая система стремится к состоянию с наименьшей потенциальной энергией. Потенциальная энергия упругой деформации характеризует взаимодействие между собой частей тела. О физическом смысле понятия потенциальной энергии Если кинетическая энергия может быть определена для одного отдельного тела, то потенциальная энергия всегда характеризует как минимум два тела или положение тела во внешнем поле. Кинетическая энергия характеризуется скоростью; потенциальная — взаиморасположением тел. Кинетическая энергия зависит от системы отсчета, а потенциальная — нет. Основной физический смысл имеет не само значение потенциальной энергии, а её изменение. Это соотношение справедливо для любого направления в пространстве, в частности и для направлений декартовых координатных осей х, у, z:  Эта формула определяет проекции вектора силы на координатные оси. Если известны эти проекции, оказывается определенным и сам вектор силы:  сила равна градиенту потенциальной энергии, взятого с обратным знаком
10. Закон сохранения полной механической энергии частицы. работа по перемещению частицы из положения 1 в положение 2 может быть выражена через приращение кинетической энергии: В общем случае на частицу могут действовать как потенциальные, так и непотенциальные силы. Таким образом, результирующая сила, действующая на частицу: Работа всех этих сил идет на приращение кинетической энергии частиц: Но, с другой стороны, работа потенциальных сил равна убыли потенциальной энергии частиц: , следовательно, . Величину называют полной механической энергией частицы. Обозначим ее через Е. Таким образом, работа непотенциальных сил идет на приращение полной механической энергии частицы. Приращение полной механической энергии частицы в стационарном поле потенциальных сил при перемещении ее из точки 1 в точку 2 можно записать в виде: Если > 0, то полная механическая энергия частицы возрастает, а если < 0, то убывает. Следовательно, полная механическая энергия частицы может измениться под действием только непотенциальных сил. Отсюда непосредственно вытекает закон сохранения механической энергии одной частицы. Если непотенциальные силы отсутствуют, то полная механическая энергия частицы в стационарном поле потенциальных сил остается постоянной. 11. Закон сохранения энергии для системы невзаимодействующих частиц. система, состоящая из невзаимодействующих элементарных частиц, обладающих каждая определённой скоростью и, следовательно, кинетической энергией Tкин. В этом случае полная энергия системы равна сумме энергий покоя всех частиц плюс сумма их кинетических энергий: Вместо mc^2 надо: Ui 12. Взаимная потенциальная энергия частиц. Закон сохранения энергии системы частиц. Потенциальная энергия тел, взаимодействующих посредством гравитационных сил. , где r- расстояние между взаимодействующими телами. Знак "-" говорит о том, что это энергия притягивающихся тел. Потенциальная (электростатическая) энергия взаимодействия зарядов. - может быть и положительной и отрицательной. собственная потенциальная энергия данной системы Преобразуем эту сумму следующим образом. Представим каждое слагаемое в симметричном виде: , ибо ясно, что . Тогда Сгруппируем члены с одинаковым первым индексом:  Каждая сумма в круглых скобках представляет собой потенциальную энергию взаимодействия частицы с остальными двумя. Поэтому последнее выражение можно переписать так: закон сохранения механической энергии: в инерциальной системе отсчета механическая энергия замкнутой системы частиц, в которой нет непотенциальных сил, сохраняется в процессе движения, т. е. энергия никогда не создается и не уничтожается, она может только переходить из одной формы в другую или обмениваться между отдельными частями материи. 13. Энергия упругой деформации. Условия равновесия механической системы. Энергию деформированного упругого тела также называют энергией положения или потенциальной энергией (ее называют чаще упругой энергией), так как она зависит от взаимного положения частей тела, например витков пружины. Работа, которую может совершить растянутая пружина при перемещении ее конца, зависит только от начального и конечного растяжений пружины. Значит, среднее значение силы равно Fср=kl. Можно показать, что для вычисления работы А изменяющейся силы упругости нужно это среднее значение силы умножить на перемещение точки приложения силы: A=1/2 kl•l=1/2kl2. Таким образом, потенциальная энергия упругости Еп равна Р 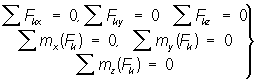 авновесие механической системы, состояние механической системы, находящейся под действием сил, при котором все её точки покоятся по отношению к рассматриваемой системе отсчёта. Если система отсчёта является инерциальной (см. Инерциальная система отсчёта),равновесие называется абсолютным, в противном случае — относительным. Изучение условий Равновесие механической системы — одна из основных задач статики. Условия Равновесие механической системы имеют вид равенств, связывающих действующие силы и параметры, определяющие положение системы; число этих условий равно числу степеней свободы системы. Условия относительности Равновесие механической системы составляются так же, как и условия абсолютного равновесия, если к действующим на точки силам прибавить соответствующие переносные силы инерции. Условия равновесия свободного твёрдого тела состоят в равенстве нулю сумм проекций на три координатные оси Oxyz и сумм моментов относительно этих осей всех приложенных к телу сил, т. е.14. Момент импульса. Момент силы. Потенциальная энергия. Связь между потенциальной энергией и силой. Момеìнт иìмпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение. Замечание: момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — скалярная величина. Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, оно также обладает моментом импульса. Наибольшую роль момент импульса играет при описании собственно вращательного движения. Момент импульса замкнутой системы сохраняется. Определение момента импульса Момент импульса L-частицы относительно некоторого начала отсчёта определяется векторным произведением ее радиус-вектора и импульса: Где r— радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчета начала отсчёта,P— импульс частицы. В системе СИ момент импульса измеряется в единицах джоуль-секунда; Дж·с. Из определения момента импульса следует его аддитивность. Так, для системы частиц выполняется выражение: Вычисление момента импульса Если имеется материальная точка массой m, двигающаяся со скоростью Vи находящаяся в точке, описываемой радиус-вектором r, то момент импульса вычисляется по формуле: где — знак векторного произведения. Чтобы рассчитать момент импульса тела, его надо разбить на бесконечно малые кусочки и векторно просуммировать их моменты как моменты импульса материальных точек, то есть взять интеграл:  |
, n - частота