ответы на экзамен вяткин 2009. Кинематика раздел механики, изучающий математическое описание (движения идеализированных тел (материальная точка, абсолютно твердое тело, идеальная жидкость), без рассмотрения причин движения (массы, сил и т д.

• Название: Кинематика раздел механики, изучающий математическое описание (движения идеализированных тел (материальная точка, абсолютно твердое тело, идеальная жидкость), без рассмотрения причин движения (массы, сил и т д.
• Анкор: ответы на экзамен вяткин 2009.doc
• Дата: 12.12.2017
• Размер: 43.45 Mb.
• Имя файла: ответы на экзамен вяткин 2009.doc
• Тип: Документы; #10885
• страница: 4 из 5

Часть теплоты при передаче неизбежно теряется, поэтому КПД двигателя менее 1. Максимально возможным КПД обладает двигатель Карно. КПД двигателя Карно зависит только от абсолютных температур нагревателя(T_H) и холодильника(T_X):

Холодильный коэффициент, безразмерная величина (обычно больше единицы), характеризующая энергетическую эффективность работы холодильной машины; равна отношению холодопроизводительности к количеству энергии (работе), затраченной в единицу времени на осуществление холодильного цикла. Определяется типом холодильного цикла, по котором у работает машина, совершенством её основных элементов и для одной и той же машины зависит от температурных условий её работы. Различают теоретический и реальный Холодильный коэффициент В частности, теоретический Холодильный коэффициент идеальной парокомпрессионной машины, работающей по обратному Карно циклу, не зависит от рода холодильного агента и определяется выражением e_к = T₀/(Т - Т₀), где T₀ и Т - абсолютные температуры охлаждаемого объекта и окружающей среды (кипения и конденсации хладагента). При заданной температуре окружающей среды Т на единицу полученного искусственного холода затрачивается тем большая энергия, чем ниже температура охлаждаемого объекта.

Формулировки второго закона термодинамики:

Постулат Клаузиуса: «Невозможен процесс, единственным результатом которого являлась бы передача тепла от более холодного тела к более горячему»

Постулат Томсона: «Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара»

«Энтропия изолированной системы не может уменьшаться» (закон неубывания энтропии).

33. Цикл Карно. Первая теорема Карно. Вторая теорема Карно.

В качестве рабочего тела в цикле Карно рассматривается идеальный газ. Цикл Карно состоит из последовательных расширения и сжатия газа, причем каждый из процессов совершается сначала изотермически, а затем адиабатически. При прямом цикле тело по-прежнему сначала получает тепло, а затем отдает его. Достоинство цикла Карно состоит в том, что все процессы обратимы, и, следовательно, КПД такой машины будет максимальным.

1-2: газ изотермически расширяется. Внутренняя энергия газа не изменяется, и количество полученного тепла Q₁равно работе А₁₂. .

2-3: газ адиабатически расширяется.

34: изотермически сжимается, для чего охладителю должно быть отдано тепло Q₂. Работа на участке 34 равна Q₂, причем .

41: газ адиабатически сжимается, возвращаясь к исходному состоянию.

Для процессов 23 и 41 цикла Карно cледует: . (TV ^γ1= const)

Разделив первое уравнение на второе, получим V₂/V₁ = V₃/V₄. После подстановки этого выражения найдем: .Следовательно, КПД цикла Карно:.

Из формулы следует, что КПД тепл машины определяется только разностью температур нагревателя и холодильника. КПД не зависит ни от свойств рабочего тела, используемого в машине, ни от свойств самой машины. Полученный результат показывает, что при T₁= T₂КПД машины равен нулю, т. е. машина не совершает работы. Работа максимальна (η = 1) при T₂= 0. Таким образом, машина тем выгоднее, чем ниже температура охладителя.

1-я теорема Карно:
"Термический к.п.д. обратимого цикла Карно не зависит от свойств рабочего тела и определяется только температурами источников".

2-я теорема Карно:
"Обратимый цикл Карно является наивогоднейшим циклом в заданном интервале температур"

34. Рабочий цикл четырёхтактного двигателя внутреннего сгорания. К.п.д. цикла.

Цикл Карно́ — идеальный термодинамический цикл. Тепловая машина Карно, работающая по этому циклу, обладает максимальным КПД из всех машин, у которых максимальная и минимальная температуры осуществляемого цикла совпадают соответственно с максимальной и минимальной температурами цикла Карно.

Цикл Карно состоит из четырёх стадий:

Изотермическое расширение (на рисунке — процесс A→Б). В начале процесса рабочее тело имеет температуру T_H, то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передаёт ему количество теплоты Q_H. При этом объём рабочего тела увеличивается.

Адиабатическое (изоэнтропическое) расширение (на рисунке — процесс Б→В). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом его температура уменьшается до температуры холодильника.

Изотермическое сжатие (на рисунке — процесс В→Г). Рабочее тело, имеющее к тому времени температуру T_X, приводится в контакт с холодильником и начинает изотермически сжиматься, отдавая холодильнику количество теплоты Q_X.

Адиабатическое (изоэнтропическое) сжатие (на рисунке — процесс Г→А). Рабочее тело отсоединяется от холодильника и сжимается без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя.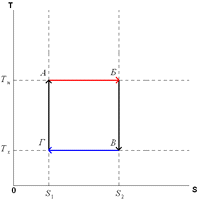

При изотермических процессах температура остаётся постоянной, при адиабатических отсутствует теплообмен, а значит, сохраняется энтропия (поскольку при δQ = 0).

Поэтому цикл Карно удобно представить в координатах T и S

Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно.

Аналогично, при изотермическом сжатии рабочее тело отдало холодильнику

.

Отсюда коэффициент полезного действия тепловой машины Карно равен

.

Из последнего выражения видно, что КПД тепловой машины Карно зависит только от температур нагревателя и холодильника. Кроме того, из него следует, что КПД может составлять 100 % только в том случае, если температура холодильника равна абсолютному нулю. Это невозможно, но не из-за недостижимости абсолютного нуля (этот вопрос решается только третьим началом термодинамики, учитывать которое здесь нет необходимости), а из-за того, что такой цикл или нельзя замкнуть, или он вырождается в совокупность двух совпадающих адиабат и изотерм.

Можно показать, что КПД любой тепловой машины, работающей по циклу, отличному от цикла Карно, будет меньше КПД тепловой машины Карно, работающей при тех же температурах нагревателя и холодильника.

35. Рабочий цикл четырёхтактного двигателя внутреннего сгорания Дизеля. К.п.д. цикла.

Цикл Дизеля — термодинамический цикл, описывающий рабочий процесс двигателя внутреннего сгорания с воспламенением впрыскиваемого топлива от разогретого рабочего тела, цикл дизельного двигателя.
Идеальный цикл Дизеля состоит из четырёх процессов: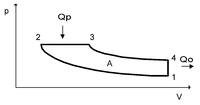


p-V диаграмма цикла Дизеля

1—2 адиабатное сжатие рабочего тела;

2—3 изобарный подвод теплоты к рабочему телу;

3—4 адиабатное расширение рабочего тела;

4—1 изохорное охлаждение рабочего тела.

КПД цикла Дизеля ,где — степень сжатия,

— коэффициент предварительного расширения,k— показатель адиабаты.

Идеальный цикл лишь приблизительно описывает процессы, происходящие в реальном двигателе, но для технических расчётов в большинстве случаев точность такого приближения удовлетворительна.

36. Неравенство Клаузиуса. Равенство Клаузиуса. Энтропия. Изэнтропический процесс. Теорема Нернста(третье начало термодинамики).

Энтропия изолированной системы не может убывать. dS≥0 (Неравенство Клаузиуса)

В случае, если термодинамический цикл состоит только из обратимых процессов, неравенство переходит в Равенство Клаузиуса:

Энтропия системы — функция её состояния, определённая с точностью до произвольной постоянной, разность которых в двух равновесных состояниях 1 и 2 по определению равна приведённому количеству теплоты, которое надо сообщить системе, чтобы перевести её из состояния 1 в состояние 2 по любому квазистатическому пути.



Закон возрастания энтропии. Энтропия адиабатически изолированной системы либо возрастает, либо остаётся постоянной.

Термин широко применяется и в других областях знания: в статистической физике — как мера вероятности осуществления какого-либо макроскопического состояния

Изоэнтропийный процесс - тепловой процесс, происходящий при постоянной энтропии.

Условия, при которых тепловой процесс будет изоэнтропийным, можно получить из равенства Клаузиуса для обратимых процессов: ,

где dS - приращение (дифференциал) энтропии, а δQ - бесконечно малое полученное количество теплоты. Отсюда следует, что из обратимых процессов изоэнтропийным является только обратимый адиабатный процесс.

Из неравенства Клаузиуса для необратимых процессов ,

следует, что необратимый адиабатный процесс не может быть изоэнтропийным.

Но вообще и при необратимом процессе энтропия системы может сохранять постоянное значение, если вся производимая энтропия сразу удаляется с помощью теплообмена.

Линию на любой термодинамической диаграмме, изображающую изоэнтропийный процесс, можно называть изоэнтропой. Но обычно её называют адиабатой, так как необратимый процесс (в том числее необратимый адиабатный) нельзя корректно изобразить линией на диаграмме.

Третье начало термодинамики (теорема Нернста) — физический принцип, определяющий поведение энтропии при абсолютном нуле температуры. Является одним из постулатов термодинамики.

«Приращение энтропии при абсолютном нуле температуры стремится к конечному пределу, не зависящему от того, в каком равновесном состоянии находится система».

или

где x — любой термодинамический параметр.

третье начало термодинамики относится только к равновесным состояниям.

Поскольку на основе второго начала термодинамики энтропию можно определить только с точностью до произвольной аддитивной постоянной (то есть, определяется не сама энтропия, а только её изменение): третье начало термодинамики может быть использовано для точного определения энтропии. При этом энтропию равновесной системы при абсолютном нуле температуры считают равной нулю.

37. Закон возрастания энтропии. Основное уравнение термодинамики.

В адиабатически изолированной термодинамической системе энтропия не может убывать: она или сохраняется, если в системе происходят только обратимые процессы, или возрастает, если в системе протекает хотя бы один необратимый процесс.

     Записанное утверждение является ещё одной формулировкой второго начала термодинамики.

     Таким образом, изолированная термодинамическая система стремится к максимальному значению энтропии, при котором наступает состояние термодинамического равновесия.

     Необходимо отметить, что если система не является изолированной, то в ней возможно уменьшение энтропии. Примером такой системы может служить, например, обычный холодильник, внутри которого возможно уменьшение энтропии. Но для таких открытых систем это локальное понижение энтропии всегда компенсируется возрастанием энтропии в окружающей среде, которое превосходит локальное ее уменьшение.

Основное неравенство термодинамики для равновесных процессов:

     В этом выражении знак равенства соответствует равновесным термодинамическим процессам, а знак неравенства - неравновесным.

38. Число степеней свободы механической системы. Поступательные, вращательные и колебательные степени свободы молекулы. Теорема о равнораспределении энергии по степеням свободы.

Число степеней свободы — это количество независимых параметров, однозначно определяющих положение механической системы.

· Простейшая механическая система — материальная точка в трёхмерном пространстве — обладает тремя степенями свободы, так как её состояние полностью описывается тремя пространственными координатами.

· Абсолютно твёрдое тело обладает шестью степенями свободы, так как для полного описания положения такого тела достаточно задать три координаты центра масс и три угла, описывающих ориентацию тела

Первоначально термин «равнораспределение» означал, что полная кинетическая энергия системы разделена одинаково среди всех её независимых частей в среднем, как только система достигла теплового равновесия. Теорема о равнораспределении также даёт количественные предсказания для этих энергий. Например, она предсказывает, что каждый атом благородного газа, находящегося в тепловом равновесии при температуре T, обладает средней кинетической энергией поступательного движения равной (3/2)k_BT. Как следствие, более тяжёлые атомы ксенона обладают более низкой средней скоростью чем лёгкие атомы гелия при той же самой температуре. Закон равнораспределения показывает, что при тепловом равновесии, любая степень свободы (компоненты векторов положения или скорость частицы), которая появляется только как квадратичная функция в энергии, обладает средней энергией равной ½k_BT и поэтому вносит вклад ½k_B в теплоёмкость системы

39. Классическая теория теплоёмкости идеальных газов.

Теплоемкость идеального газа - это отношение тепла, сообщенного газу, к изменению температуры δТ, которое при этом произошло.

Молярная теплоемкость - теплоемкость 1 моля идеального газа.

где i - число степеней свободы частиц газа. C_P=δQ/νΔT=C_V+R=(1+i/2)*R

В изотермическом процессе постоянна температура, т.е. dT = 0. Следовательно, теплоемкость идеального газа стремится к бесконечности:

В адиабатическом процессе теплообмена с окружающей средой не происходит, т.е. δQ=0. Следовательно, теплоемкость идеального газа в адиабатическом процессе также равна нулю: С_адиаб=0.

40. Классическая теория теплоёмкости твёрдых тел (кристаллов). Закон Дюлонга и Пти.

Закон Джоуля-Коппа описывает теплоёмкость сложных (т.е. состоящих из нескольких химических элементов) кристаллических тел. Основан на законе Дюлонга-Пти. Каждый атом в молекуле имеет

три колебательных степени свободы, и он обладает энергией . Соответственно, молекула из n атомов обладает в n раз большей энергией:

Молярная теплоёмкость вещества равна:

то есть она в n раз больше теплоёмкости кристалла с одноатомными молекулами. Иными словами, молярная теплоёмкость вещества равна сумме теплоёмкостей составляющих его химических элементов. Важно отметить, что закон Джоуля-Коппа выполняется даже для кристаллов, содержащих в своей структуре не подчиняющиеся закону Дюлонга-Пти химические элементы.

Закон Дюлонга-Пти (Закон постоянства теплоёмкости) — эмпирический закон, согласно которому молярная теплоёмкость твёрдых тел при комнатной температуре близка к 3R:где R — универсальная газовая постоянная.

Закон выводится в предположении, что кристаллическая решетка тела состоит из атомов, каждый из которых совершает гармонические колебания в трех направлениях, определяемыми структурой решетки, причем колебания по различным направлениям абсолютно независимы друг от друга. При этом получается, что каждый атом представляет три осциллятора с энергией E, определяемой следующей формулой:.

Формула вытекает из теоремы о равнораспределении энергии по степеням свободы. Так как каждый осциллятор имеет одну степень свободы, то его средняя кинетическая энергия равна K=kt/2, а так как колебания происходят гармонически, то средняя потенциальная энергия равна средней кинетической, а полная энергия - соответственно их сумме. Число осцилляторов в одном моле вещества составляет , их суммарная энергия численно равна теплоемкости тела - отсюда и вытекает закон Дюлонга-Пти.