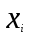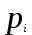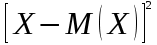математика. Классическое определение вероятности
 Скачать 178.33 Kb. Скачать 178.33 Kb.
|
|
КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ Испытание – это изначальное понятие, разъясняется как действие, наблюдение, опыт и прочее. Событие – это результат испытания. Событие, которое в результате испытания может произойти, а может и не произойти, называется случайным. Пример 1. монета может упасть не гербом, а решкой (цифрой) вверх. Аналогично, в результате подбрасывания кубика может выпасть, например, два или пять очков. Пусть в результате испытания могут появиться несколько событий. События называются несовместными, если появление одного из них исключает появление других. В противном случае, события называются совместными. Пример 2. Рассмотрим такое испытание, как сдача экзамена по математике одним из студентов. События, которые, например, могут произойти в результате этого испытания, есть следующие: А – экзамен сдан на оценку «4», В – экзамен сдан на оценку «3», С – экзамен сдан на оценку выше, чем «3». В этом случае, события А и В несовместны, так как получение оценки «3» делает невозможным получение оценки «4» за этот же экзамен. Наоборот, события А и С совместны, поскольку они могут произойти одновременно. Пример 3. Произведено испытание ˗ психолог предъявил обследуемому вопрос. По условиям испытания обследуемый может дать только один из двух ответов: «да» или «нет». Отсюда, результатом испытания может быть только одно из двух несовместных событий. Пространством элементарных исходов (или событий), соответствующих рассматриваемому испытанию, будем называть такое множество несовместных событий, одно из которых обязательно произойдет в результате испытания, так что любой интересующий нас результат испытания может быть однозначно описан с помощью элементов этого множества. Пример 4. игральные кубики ˗ пространство элементарных исходов образуют 6 событий: E1, E2, E3, E4, E5, E6, которые заключаются в том, что количество выпавших очков составит соответственно 1, 2, 3, 4, 5 или 6 очков. Действительно, эти события несовместны, одно из них обязательно произойдет в результате подбрасывания кубика, и с их помощью можно описать любые другие события. Например, событие A – выпало четное число очков – означает, что появились события E2или E4 или E6, эти три элементарных исхода благоприятствуют наступлению события A. Равновозможные события, если по условиям симметрии нет оснований считать появление какого-либо из них более возможным по отношению к другим, т.е. все события имеют равные “шансы”. Достоверным называются событие, которое обязательно наступит в результате испытания. Невозможным называются событие, которое в результате испытания заведомо не произойдет. Несколько событий образуют полную группу, если они попарно несовместны и в результате испытания появление хотя бы одного из них и является достоверным событием. Отсюда следует, что если события, образуют полную группу, попарно несовместны, то в результате испытания появится только одно из этих событий. Пример 5. Игральная кость – это однородный кубик, на гранях которого изображено количество очков от 1 до 6, так как всего граней 6. Испытание – бросание игральной кости. Событие – выпадение определенного количества очков на верхней грани. Полную группу событий образуют шесть событий: E1, E2, E3, E4, E5, E6, которые заключаются в том, что количество выпавших очков составит соответственно 1, 2, 3, 4, 5 или 6 очков. По условию симметрии игральной кости все шесть элементарных исходов являются равновозможными. Пусть событие A – «количество выпавших очков ˗ четное число». Это означает, что появились события E2 или E4 или E6 . По этим трем элементарным исходам можно судить о появлении события A. Эти три интересующие нас события называют благоприятнымисобытиями. Если событие B –«количество выпавших очков больше четырех», то это означает, что благоприятными являются события E5 и E6. Вероятностью события A называется число P(A), равное отношению числа элементарных исходов m, благоприятствующих событию A, к общему числу элементарных равновозможных исходов n, образующих полную группу: 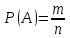 (1) (1)Для достоверного события все исходы благоприятные, то есть m = n: 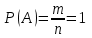 (2) (2)Для невозможного события, которое не может произойти в результате испытания, m = 0: 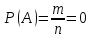 (3) (3)Для случайного события, которое может произойти, а может и не произойти в результате испытания: 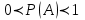 (4) (4)Пример 5. В примере с игральной костью всего элементарных равновозможных исходов n = 6, поэтому, если событие A – «количество выпавших очков ˗ четное число», а событие B – «количество выпавших очков больше четырех», то: 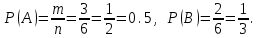 Пример 6. Пусть в урне 20 одинаковых шаров (по размеру, температуре, гладкости), которые отличаются только цветом, например, 12 из них красные, а остальные – белые. Испытание – извлечение наугад одного шара. Событие А – появление красного шара. Решение: Очевидно, что всего элементарных исходов n = 20 (по количеству шаров), причём все эти исходы равновозможные. Благоприятными являются 12 исходов (по количеству красных шаров), поэтому: 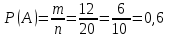 Вероятность является числовой мерой объективной возможности наступления события. Вероятность можно задавать в процентах, например P(A)= 0,8 или (80%). ОСНОВНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ Суммой А+В (А или В) двух событий А и В называется событие, состоящее в появлении события А, или события В, или обоих этих событий. Произведением А·В (А и В) двух событий А и В называется событие, состоящие в совместном появлении этих событий. Условной вероятностью РА(В) называется вероятность события В, вычисленная в предположении, что событие А уже наступило. Пример 7. В урне имеется 3 белых и 2 черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно. Найти вероятность появления белого шара во втором испытании (событие В) при условии, что в первом испытании был извлечен черный шар (событие А). Решение. Изначально в урне было 5 шаров, из которых 3 белых и 2 черных. После первого испытания, то есть извлечения чёрного шара, в урне осталось 4 шара, из них 3 белых и 1 чёрный. Искомая условная вероятность РА(В)= 3/4. События А и В называются независимыми, если появление одного из этих событий не изменяет вероятности наступления другого, то есть Р(А)= РВ(А) или Р(В)= РА(В). В противном случае события называются зависимыми. Теорема сложения вероятностей несовместных событий: P(A + B) = P(A) + P(B) . Теорема умножения вероятностей независимых событий: P(A ⋅ B) = P(A)⋅ P(B) . Теорема умножения вероятностей зависимых событий: P(A⋅B)=P(A) ⋅PА(B). Теорема сложения вероятностей совместных событий: P(A + B) = P(A) + P(B) − P(A⋅ B). Противоположным событию A называется событие A (не A),если оно наступает тогда и только тогда, когда событие A не наступает. Пример 7. а) Событие A – изделие бракованное, событие 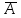 – изделие без брака, в) Событие B – студент сдал экзамен, событие – изделие без брака, в) Событие B – студент сдал экзамен, событие 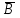 – студент не сдал экзамен, с) Событие С – хотя бы один лотерейный билет выиграл, событие – студент не сдал экзамен, с) Событие С – хотя бы один лотерейный билет выиграл, событие 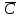 – ни один лотерейный билет не выиграл. – ни один лотерейный билет не выиграл.Из приведенных примеров видно, что противоположное событие можно сформулировать путем простого логического отрицания. Вероятность противоположного события находится по формуле: 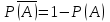 (5) (5)ФОРМУЛА ЧИСЛА СОЧЕТАНИЙ Пусть имеется n различных объектов. Чтобы найти число сочетаний из n объектов по k, будем выбирать комбинации из m объектов все возможными способами, при этом будем обращать внимание на разный состав комбинаций, но не порядок (он тут не важен, в отличие от размещений). Например, есть три объекта {1,2,3}, составляем сочетания по 2 объекта в каждом. Тогда выборки {1,2} и {2,1} - это одно и то же сочетание (так как комбинации отличаются лишь порядком). А всего различных сочетаний из 3 объектов по 2 будет три: {1,2}, {1,3}, {2,3}. На рис. 1 наглядно проиллюстрировано получение всех возможных сочетаний из 4 различных объектов по 2 (их будет 6), так как: 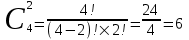 способов. способов.Общая формула, которая позволяет найти число сочетаний из n объектов по k имеет вид: 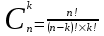 (6) (6) Рис. 1 Пример 8. В группе 7 мужчин и 4 женщины, надо выбрать 6 человек так, чтобы среди них было не менее 2 женщин. Сколькими способами это можно сделать? Решение: можно выбрать 2, 3 или 4 женщин, напомним, что n – всего объектов, а k – кого выбираем, тогда 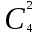 ˗ 2 женщины из возможных 4, ˗ 2 женщины из возможных 4,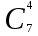 ˗ 4 мужчин из возможных 7, по правилу произведения получим: ˗ 4 мужчин из возможных 7, по правилу произведения получим: 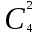 ˟ ˟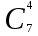 и так далее. и так далее.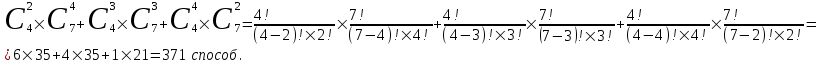 Задачи для самостоятельного решения №1. В корзине 52 шара: 31 красных и 21 синих. Вынули два шара. Какова вероятность, что оба шара красных? №2. Из колоды в 36 карт вынимается одна карта. Какова вероятность появления карты червовой масти? №3. На предприятии занято производством 42 человека (20 женщин, 22 мужчины). Был открыт новый цех по производству. Для перенаправления в другой цех наугад было выбрано 11 человек. Найти вероятность того, что среди отобранных лиц окажутся 5 женщин. №4.Абонент забыл последнюю цифру номера телефона и поэтому набирает её наугад. Определить вероятность того, что ему придётся звонить не более чем в 3 места. №5. Абонент забыл последние 2 цифры телефонного номера, но помнит, что они различны и образуют двузначное число, меньшее 30. С учетом этого он набирает наугад 2 цифры. Найти вероятность того, что это будут нужные цифры. №6. На шахматную доску случайным образом поставлены две ладьи. Какова вероятность, что они не будут бить одна другую? №7. Цифры 1, 2, 3, …, 20, выписанные на отдельные карточки складывают в ящик и тщательно перемешивают. Наугад вынимают одну карточку. Найти вероятность того, что число, написанное на этой карточке: а) четное; б) двузначное. №8. На полке в случайном порядке расставлено 58 книг, среди которых находится 4˗х томник. Найти вероятность того, что эти тома стоят в порядке возрастания номера слева направо, но не обязательно рядом. №9. На каждой из одинаковых карточек напечатана одна из следующих букв: «т», «с», «ю», «о», «ф», «л», «н». Карточки тщательно перемешаны. Найти вероятность того, что на четырех вынутых по одной карточке можно прочесть слово «стол». №10. В магазине выставлены для продажи 40 изделий, среди которых 6 изделий имеют брак. Какова вероятность того, что наудачу взятые 5 изделий, 3 из них окажутся с браком. ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ События H1 , H2 , …, Hn образуют полную группу, если они попарно несовместны и в результате испытания одно из них обязательно произойдет. Для таких событий справедливо равенство: 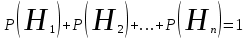 (7) (7)Противоположные события A и 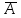 всегда образуют полную группу, поэтому всегда образуют полную группу, поэтому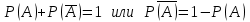 (8) (8)Пусть событие A наступает с одним из событий (гипотез) Hi, тогда вероятность этого события находится по формуле, называемой формулой полной вероятности 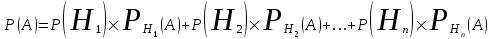 (9) (9)ФОРМУЛА БАЙЕСА По этой формуле находится вероятность наступления гипотезы НR при условии, что событие А произошло: 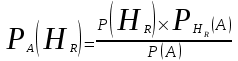 (10) (10)Здесь в знаменателе стоит вероятность события А, вычисляемая по формуле полной вероятности, а в числителе – одно из слагаемых формулы полной вероятности, соответствующее гипотезе НR. Задачи для самостоятельного решения №11. Вероятность того, что новый товар будет пользоваться спросом на рынке, если конкурент не выпустит в продажу аналогичный продукт, равна 0,75 , а при наличии конкурирующего товара равна 0,35. Вероятность выпуска конкурентом товара равна 0,45. Найти вероятность того, что товар будет пользоваться спросом. №12. Курс доллара повышается в течение квартала с вероятностью 0,9 и понижается с вероятностью 0,1. При повышении курса доллара фирма рассчитывает получить прибыль с вероятностью 0,85; при понижении – с вероятностью 0,5. Найти вероятность того, что фирма получит прибыль. Оказалось, что фирма получила прибыль, какова вероятность, что это произошло при понижении (повышении) курса доллара? №13. На строительство объекта поступают железобетонные плиты от четырех цементных заводов в количестве 50, 10, 40 и 30 штук соответственно. Каждый из заводов допускает при изготовлении плит брак (несоответствие ГОСТ), составляющий соответственно 1%, 5%, 2% и 3%. Какова вероятность того, что наугад взятая плита будет удовлетворять требованиям ГОСТ? Оказалось, выбранная деталь, удовлетворяет требованиям гост. Какова вероятность, что эта плита изготовлена 2 и 4 цементным заводом? №14. В цехе трудятся 3 мастера и 6 их учеников. Мастер допускает брак при изготовлении изделия с вероятностью 0,05; а ученик – с вероятностью 0,15. Какова вероятность, что взятое наугад изделие будет бракованным? №15. В данный район изделия поставляются двумя фирмами. Среди продукции первой фирмы стандартные изделия составляют 90%, у второй фирмы этот показатель 85%. Какова вероятность, что взятое наугад изделие оказалось стандартным, если вероятность того, что оно поставлено первой фирмой, равна 0,4? №16. В магазине имеются два телевизора с импортными и девять с отечественными трубками. Вероятность выхода из строя в течение гарантийного срока телевизора с импортной трубкой равна 0,005; с отечественной трубкой равна 0,01. Найти вероятность того, что купленный в магазине телевизор выдержит гарантийный срок. №17. В двух ящиках находятся радиолампы. В первом ящике 3% ламп ˗ бракованные, во втором ящике бракованные лампы составляют 5%. Из наудачу выбранного ящика выбирается одна лампа. Найти вероятность того, что она будет без брака. №18. Страховая компания разделяет застрахованных клиентов по классам риска: I класс – малый риск, II класс – средний риск, III класс – большой риск. Среди этих клиентов 50 % ˗ первого класса риска, 30% ˗ второго и 20% ˗ третьего. Вероятность необходимости выплачивать страховое вознаграждение для первого класса риска равна 0,01, второго 0,03, третьего 0,08. Какова вероятность того, что застрахованный получит денежное вознаграждение за период страхования? Пусть, страховой случай наступил, какова вероятность, что выплата придется на клиента 1, 2 и 3 класса? №19. Вся продукция цеха проверяется двумя контролерами, причем первый контролер проверяет 55% изделий, а второй – остальные. Вероятность того, что первый контролер пропустит нестандартное изделие, равна 0,01, а для второго контролера эта вероятность 0,02. Какова вероятность, что взятое наугад изделие, маркированное как стандартное, оказалось нестандартным? №20. Вероятность изготовления изделия с браком на данном предприятии равна 0,04. Перед выпуском изделие подвергается упрощенной проверке, которая в случае бездефектного изделия пропускает его с вероятностью 0,92, а в случае изделия с дефектом – с вероятностью 0,03. Определить, какая часть изготовленных изделий выходит с предприятия. ПОВТОРЕНИЕ НЕЗАВИСИМЫХ ИСПЫТАНИЙ (ФОРМУЛА БЕРНУЛЛИ, ЛАПЛАСА) Пусть известна вероятность появления события А в каждом испытании: 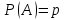 , тогда , тогда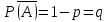 – вероятность не появления события А. Испытание повторяется n раз. Требуется найти вероятность того, что событие А наступит при этом ровно k раз. Обозначим – вероятность не появления события А. Испытание повторяется n раз. Требуется найти вероятность того, что событие А наступит при этом ровно k раз. Обозначим 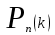 – вероятность того, что в n испытаниях событие А наступит k раз. Эта вероятность находится по формуле Бернулли: – вероятность того, что в n испытаниях событие А наступит k раз. Эта вероятность находится по формуле Бернулли: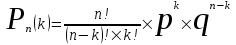 (11) (11)Формулу Бернулли обычно применяется, если число повторных испытаний невелико (n ≤ 10). Если число испытаний велико (n >10), то вместо формулы Бернулли используется локальная формула Лапласа, которая является приближенной: 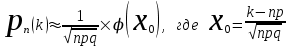 (12) (12)Значение функции 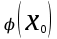 берётся по таблице (см. прил. 1). Если число испытаний велико (n >10) и нужно найти вероятность того, что при n испытаниях событие А наступит от k1 до k2 раз, то применяют интегральную формулу Лапласа, которая также берётся по таблице (см. прил. 1). Если число испытаний велико (n >10) и нужно найти вероятность того, что при n испытаниях событие А наступит от k1 до k2 раз, то применяют интегральную формулу Лапласа, которая такжеявляется приближенной: 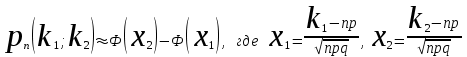 (13) (13)Значения функции Лапласа Ф(x) берут по таблице (прил. 2). Приближенные формулы дают тем более точный результат, чем больше значение n. НАИВЕРОЯТНЕЙШЕЕ ЧИСЛО ПОЯВЛЕНИЙ СОБЫТИЯ Пусть в n повторных испытаниях событие А появляется k раз, где k может принимать значения: 0; 1; 2; …; n (то есть 0 ≤ k ≤ n). Для каждого из этих значений k можно найти соответствующую ему вероятность по формуле Бернулли. Значение k, которому соответствует самая большая вероятность, называется наивероятнейшим числом появления события А. Наивероятнейшее число k0 находится как целое число из промежутка: np − q ≤ k ≤ np + p (14) При этом k0 может принимать либо одно значение, либо два соседних целых значения с одинаковой вероятностью. Вероятность 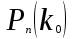 , соответствующую значению k = k0, находим по формуле Бернулли. , соответствующую значению k = k0, находим по формуле Бернулли. ПОЯВЛЕНИЕ СОБЫТИЯ ХОТЯ БЫ ОДИН РАЗ Вероятность появления события «хотя бы один раз» в n испытаниях находится с помощью противоположного ему события «ни одного раза»: 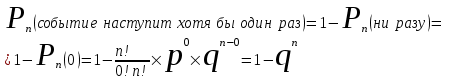 (15) (15)где 0!=1 и р0=1 Событие наступит «хотя бы один раз» означает, что оно наступит один или более раз, поэтому можно записать: pn(k≥1)=1˗qn Задачи для самостоятельного решения №21. Произвели 17 выстрелов. Вероятность попадания при одном выстреле равна 0,705. Найти вероятность того, что при этом будет ровно 12 попаданий. №22. Вероятность попадание в мишень при одном выстреле равна 0,3. По мишени произвели 14 независимых выстрелов. Найти вероятность того, что будет хотя бы одно попадание. №23. Вероятность попадания в мишень стрелком равна 0,6, найти вероятность того, что при 9 выстрелах мишень будет поражена от 5 до 8 раз. №24. Вероятность хотя бы одного попадания в цель при 6 выстрелах равна 0,9819. Найти вероятность попадания в цель при одном выстреле. №25. В дачном поселке всего установлено 7900 штук ламп уличного освещения. Из˗за перебоев в системе снабжения электричеством, вероятность включения каждой из них зимой после 17.00 часов составляет 0,6. Какова будет вероятность того, что одновременно включенных ламп будет от 4100 до 4800. Найти наименьшее число включенных ламп среди 7900 и соответствующую вероятность. №26. Производственный станок в целом состоит из 1500 элементов, работающих независимо друг от друга. Вероятность того, что откажет один из элементов, равна 0,036. Найти вероятность того, что откажут 42 элемента. №27. Какова вероятность того, что если бросить монету 1600 раз, орел выпадет от 720 до 880 раз? ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ Если случайное событие выражается в виде числа, можно говорить о случайной величине. Случайной называют величину, которая в результате испытания примет одно возможное значение, наперёд неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены. Выпадение некоторого значения случайной величины Х это случайное событие: Х = хi. Среди случайных величин выделяют дискретные и непрерывные случайные величины. Дискретной случайной величиной называется случайная величина, которая в результате испытания принимает отдельные значения с определёнными вероятностями. Число возможных значений дискретной случайной величины может быть конечным и бесконечным. Примеры дискретной случайной величины: запись показаний спидометра или измеренной температуры в конкретные моменты времени. Непрерывной случайной величиной называют случайную величину, которая в результате испытания принимает все значения из некоторого числового промежутка. Число возможных значений непрерывной случайной величины бесконечно. Пример непрерывной случайной величины: измерение скорости перемещения любого вида транспорта или температуры в течение конкретного интервала времени. Любая случайная величина имеет свой закон распределения вероятностей и свою функцию распределения вероятностей. Функцией распределения случайной величины Х называется функция F(х), определяющая вероятность того, что случайная величина Х в результате испытания примет значение меньшее значения х, то есть: F (х) = Р(Х < х ), где х – произвольное действительное число. Случайная величина (непрерывная или дискретная) имеет численные характеристики: Математическое ожидание М(Х) (ожидаемое среднее значение случайной величины). Эту характеристику можно сравнивать со средним арифметическим наблюдаемых значений случайной величины Х: 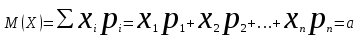 (16) (16)Дисперсия D(X). Это характеристика отклонения случайной величины Х от математического ожидания или мера рассеяния значений случайной величины Х от среднего значения а: 1 способ:Через определение дисперсии, то есть: Дисперсия дискретной случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: 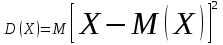 (17) (17)2 способ:Через формулу для дисперсии, то есть: 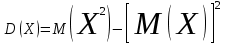 (18) (18)Среднее квадратическое отклонение s(Х) (характеристика рассеяния в единицах признака Х): для дискретной и непрерывной случайной величины Х – это корень квадратный из ее дисперсии: 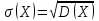 (19) (19)Законом распределения дискретной случайной величины называют соответствие между полученными значениями дискретной случайной величины и их вероятностями. Его можно задать: таблично (рядом распределения); графически; аналитически (в виде формулы). Пример 9. В рекламных целях торговая фирма вкладывает в свой товар случайным образом некоторые призы. На каждые100 единиц товара приходится 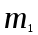 призов стоимостью призов стоимостью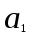 рублей, рублей, 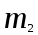 призов стоимостью призов стоимостью 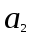 рублей, рублей, 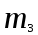 призов стоимостью призов стоимостью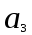 рублей и т. д. В остальных единицах товара призов нет. рублей и т. д. В остальных единицах товара призов нет. Составить закон распределения величины стоимости приза для покупателя, который приобрел одну единицу товара этой фирмы, и найти его основные характеристики: математическое ожидание, дисперсию (двумя способами) и среднее квадратическое отклонение. Пояснить смысл полученных результатов. Найти вероятность того, что покупатель одной единицы товара станет обладателем выигрыша не менее 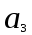 рублей. рублей.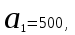 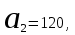 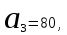 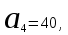 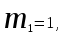 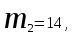 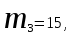 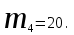 Решение: Обозначим Х тыс. руб. – величина выигрыша на один билет, очевидно, что Х, есть случайная величина, тогда: 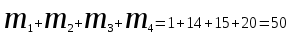 ˗ билетов являются выигрышными, ˗ билетов являются выигрышными, 100˗50=50 – билетов не выигрывают. Расположим величины возможного выигрыша в порядке возрастания, следовательно, закон распределения дискретной случайной величины Х есть: 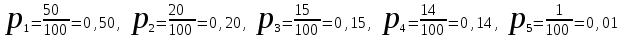 , ,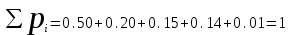 Таблица 1 Закон распределения дискретной случайной величины Х
Математическое ожидание: 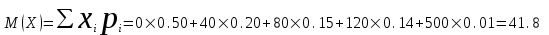 Следовательно, ожидаемый средний выигрыш на один билет составляет 41,8 руб. Дисперсию (двумя способами): 1 способ: Через определение дисперсии, то есть: Дисперсия дискретной случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: 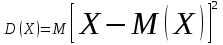 Нам известна величина 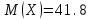 , найдем все возможные квадрат отклонения: , найдем все возможные квадрат отклонения: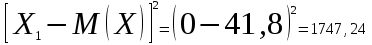 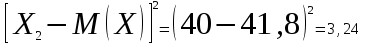 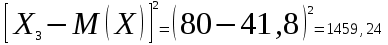 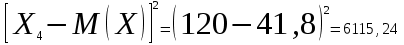 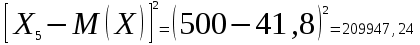 Тогда закон распределения квадрата отклонения отклонений есть:
Тогда, по определению дисперсии: 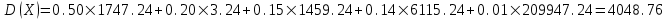 2 способ:Через формулу для дисперсии, то есть: 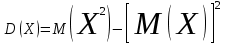 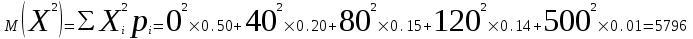 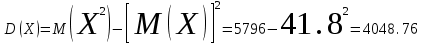 Очевидно, что результаты вычислений дисперсии обоими способами совпадают. Среднее квадратическое отклонение: 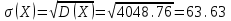 руб. руб.Таким образом, характеристика разброса фактических значений выигрыша от найденного среднего значения 41,8 руб. составляет 63,63 руб., то есть основные значения случайной величины выигрыша находятся в диапазоне 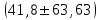 руб., что соответствует данным задачи. руб., что соответствует данным задачи.Найдем вероятность того, что покупатель одной единицы товара станет обладателем выигрыша не менее 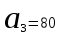 рублей. рублей.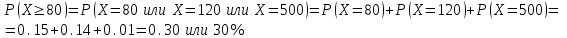 Ответ: 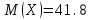 , , 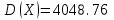 , ,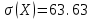 , ,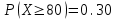 . .Задачи для самостоятельного решения №28. На пути движения автомашины 4 светофора, каждый из которых запрещает дальнейшее движение автомашины с вероятностью 0,5. Найти ряд распределения числа светофоров, пройденных машиной до первой остановки. Чему равны математическое ожидание и дисперсия этой случайной величины? №29. Охотник стреляет по дичи до первого попадания, но успевает сделать не более четырех выстрелов. Составить закон распределения числа промахов, если вероятность попадания в цель при одном выстреле равна 0,7. Найти дисперсию этой случайной величины. |