|
|
Химия шпоры. Химия (Ответы на вопросы). Классификация основных классов неорганических веществ. Составление формул и номенклатура химических соединений
28. Связь КС с Кр и КР. Принцип Ле-Шателье. Факторы, влияющие на смещение химического равновесия.
принцип Ле-Шателье: если изменить одно из условий, при котором система находится в состоянии равновесия – концентрацию, давление или температуру, — то равновесие сместится в направлении той реакции, которая противодействует этому изменению.
Т.е. равновесие стремится к смещению в направлении, приводящему к уменьшению влияния воздействия, которое привело к нарушению состояния равновесия.
Состояние, при котором скорости прямой и обратной реакций равны между собой, называется химическим равновесием. Уравнение обратимой реакции в общем виде:
mA+nB  pC+qD
Скорость прямой реакции v1=k1[A]m[B]n, скорость обратной реакции v2=k2[С]p[D]q, где в квадратных скобках – равновесные концентрации. По определению, при химическом равновесии v1=v2, откуда
Кс =k1/k2 = [С]p[D]q / [A]m[B]n,
Факторы, влияющие на химическое равновесие.
1. Влияние температуры. В каждой обратимой реакции одно из направлений отвечает экзотермическому процессу, а другое - эндотермическому.
При повышении температуры химическое равновесие смещается в направлении эндотермической реакции, при понижении температуры - в направлении экзотермической реакции.
2. Влияние давления. Во всех реакциях с участием газообразных веществ, сопровождающихся изменением объема за счет изменения количества вещества при переходе от исходных веществ к продуктам, на положение равновесия влияет давление в системе.
Влияние давления на положение равновесия подчиняется следующим правилам:
При повышении давления равновесие сдвигается в направлении образования веществ (исходных или продуктов) с меньшим объемом.
3. Влияние концентрации. Влияние концентрации на состояние равновесия подчиняется следующим правилам:
При повышении концентрации одного из исходных веществ равновесие сдвигается в направлении образования продуктов реакции;
при повышении концентрации одного из продуктов реакции равновесие сдвигается в направлении образования исходных веществ.
Закон действующих масс может быть выражен через константы равновесия Кc, Кр и Кх которые связаны между собой.
а) Если все реагенты ХР- газообразные вещества, то закон действующих масс имеет вид
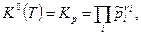
где 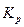 - константа равновесия, выраженная через парциальные давления. - константа равновесия, выраженная через парциальные давления.
Выразим 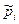 через молярные доли xi: через молярные доли xi: 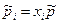 и подставим в: и подставим в:
Тогда получим:
 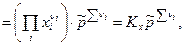
где 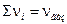 - стехиометрические коэффициенты только газообразных веществ; Кх – константа равновесия, выраженная через молярные доли: - стехиометрические коэффициенты только газообразных веществ; Кх – константа равновесия, выраженная через молярные доли:
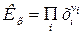
где 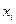 - молярные доли всех участников реакции. - молярные доли всех участников реакции.
Связь Кх с Кр будет иметь вид:
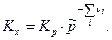
б) Выразим 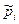 через молярные концентрации через молярные концентрации 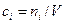 , моль/м3 и запишем уравнение состояния для i-го компонента смеси идеальных газов в виде: , моль/м3 и запишем уравнение состояния для i-го компонента смеси идеальных газов в виде: 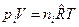 . Тогда получим . Тогда получим 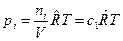 , или после деления на величину давления в одну физическую атмосферу: , или после деления на величину давления в одну физическую атмосферу:
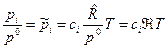
где 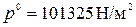 ; ; 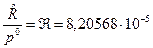 , [м3/моль×К]. , [м3/моль×К].
После подстановки 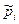 (выражение (14)) в (10) имеем: (выражение (14)) в (10) имеем:
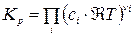 = = 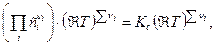
где Кс - константа равновесия, выраженная через молярные концентрации сi, равна:
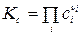
Тогда связь Кс с Кр будут иметь вид:
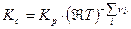
Таким образом связь между Кр, Кх и Кс имеет вид
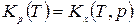 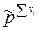 = = 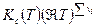 . .
Связь энергии Гиббса с константой химического равновесия.
В химической термодинамике имеется соотношение, ĸᴏᴛᴏᴩᴏᴇ связывает энергию Гиббса с константой равновесия. Это широко известное уравнение Вант-Гоффа, ĸᴏᴛᴏᴩᴏᴇ записывается в линейном и экспотенциальном виде:
Рассчитав величину DG0298 химической реакции, можно определить константу равновесия
Для реакции, протекающей в изобарно-изотермических условиях, в некотором неравновесном исходном состоянии энергии Гиббса или химические потенциалы реагирующих веществ и продуктов реакции в общем случае не одинаковы, их разность (ΔGT) может быть рассчитана по уравнению:
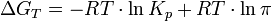
где 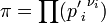 — отношение парциальных давлений участников реакции в исходном состоянии в степенях, равных их стехиометрическим коэффициентам; R — универсальная газовая постоянная. — отношение парциальных давлений участников реакции в исходном состоянии в степенях, равных их стехиометрическим коэффициентам; R — универсальная газовая постоянная.
Это уравнение называют уравнением изотермы химической реакции. Оно позволяет рассчитать изменение энергии Гиббса при протекании процесса и определить направление протекания реакции:
при 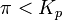 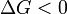 — реакция идёт в прямом направлении, слева направо; — реакция идёт в прямом направлении, слева направо;
при 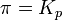 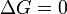 — реакция достигла равновесного состояния; — реакция достигла равновесного состояния;
при 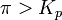 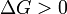 — реакция идёт в обратном направлении. — реакция идёт в обратном направлении.
Стандартная константа равновесия связана со стандартной энергией Гиббса реакции соотношением:
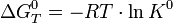
Стандартная энергия Гиббса реакции в газовой смеси — энергия Гиббса реакции при стандартных парциальных давлениях всех компонентов, равных 0,1013 МПа (1 атм).
Планетарная модель строения атома. Строение атома(ядро, электрон, протон, нейтрон, нуклоны). Изотопы, изотоны, изобары. Строение ядер.
Ядро атома состоит из нуклонов: протонов и нейтронов. Общее число нуклонов в ядре называют массовым числом А. Число протонов в ядре равно порядковому номеру в системе элементов Менделеева Z (числу протонов в ядре или числу электронов в атоме), число нейтронов
Ядро обозначают символом.
Ядра могут иметь несколько изотопов, характеризующимися одним и тем же порядковым номером Z, но различными А и N. Например, – ядро водорода – протон; – ядро дейтерия – дейтрон (d); – ядро трития – тритон (t).
Электрический заряд ядра равен числу положительно заряженных протонов в ядре. Размеры ядер зависят от числа нуклонов в ядре, и как у всякой квантовой системы у атомного ядра нет четко выраженной границы.
Протон - элементарная частица в составе атомного ядра массой 1,67-10
24 г, имеющая положительный заряд 1,6-10"19 Кл. Протон был открыт в 1920 г. английским физиком Э. Резерфордом.
Нейтрон - элементарная частица в составе атомного ядра массой 1,67 •10
24 г. Не заряжена. Нейтрон был открыт в 1932 г. английским физиком Дж. Чедвиком. Сумму протонов и нейтронов называют нуклонами.
В состав ядра, кроме протонов и нейтронов, входит множество других микрочастиц, таких как мюоны, нейтрино, т-лептоны, гипероны, ц-мюзоны, 7г-мюзоны, кварки (5 видов), антикварки (5 видов) и др.
Изотопы - разновидности атомов, имеющих одинаковые заряды ядер, но разные атомные массы (за счет разного числа нейтронов в ядре), напри мер, Mg и Mg, С1и С1.
94 9S "3S37
Самопроизвольное превращение неустойчивого изотопа одного химического элемента в изотоп другого элемента, сопровождающееся испусканием элементарных частиц или ядер (ос-частицы), называется радиоактивностью.
Изобары - это атомы, имеющие одинаковые массовые числа, но различные заряды ядер и разные химические свойства. Например, атомы аргона, калия и кальция - 40Аг, 40К, 40Са.
Ядра с одинаковым числом протонов и разным числом нейтронов называются изотопами. Ядра с одинаковым числом нейтронов, но разным числом протонов — называются изотонами.
Планета́рная моде́ль а́тома, или модель атома Резерфо́рда, — исторически важная модель строения атома, предложенная Эрнстом Резерфордом в классической статье[1], опубликованной в 1911 г. на основании анализа и статистической обработки результатов экспериментов по рассеиванию альфа-частиц в тонкой золотой фольге, выполненных Гейгером и Марсденом в 1909 г.
В этой модели Резерфорд описывает строение атома состоящим из крохотного положительно заряженного ядра, в котором сосредоточена почти вся масса атома, вокруг которого вращаются электроны, — подобно тому, как планеты движутся вокруг Солнца.
31.Противоречия планетарной модели строения атома. Постулаты Бора.
Основным недостатком планетарной модели строения атома Резерфорда было ее противоречие теории классической электродинамики, которая утверждает, что, двигаясь по круговой орбите, электрон как заряженная частица должен непрерывно излучать энергию и "достаточно быстро упасть на ядро". Нильс Бор пришел к выводу, что микрочастицы отличаются по свойствам от макрообъектов, поэтому классической электродинамики недостаточно для их описания. В своей теории Бор использовал представления классической механики о движении заряженной частицы в электрическом поле, дополнив их идеями квантования энергии. При этом он выдвинул три постулата (постулат – утверждение в теории, принимаемое за истинное, хотя и недоказуемое в рамках этой теории).
Первый постулат. Электроны в атоме могут двигаться только по некоторым определенным устойчивым стационарным круговым орбитам. При движении по этим орбитам электроны не излучают энергию, то есть существует ряд стационарных состояний атома, соответствующих определенным значениям его энергии.
Второй постулат.При переходе электрон с одной стационарной орбиты на другую атом испускает или поглощает квант электромагнитного излучения, энергия которого (hn) равна разности энергий стационарных состояний: hn=E1–E2,
где h – постоянна планка, n – частота излучения.
Третий постулат. В атоме существуют только такие электронные орбиты, находясь на которых электрон обладает моментом количества движения, кратным 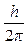 (часто вводят обозначение (часто вводят обозначение 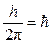 ): ):
M = m×v×r = 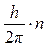 , ,
где M – момент количества движения электрона; m = 9,11×10-31 кг – масса электрона; v – скорость электрона; r – радиус орбиты электрона; h = 6,63×10-34Дж×с – постоянная Планка; n = 1,2,3 ... – целое число, получившее название «квантовое число».
Используя эти постулаты, Бор рассчитал размеры стационарных орбит электронов в атоме, энергию электронов на стационарных орбитах и выразил постоянную Ридберга через основные константы.
32Теория строения атома Бора- Зоммерфельда.
Теория Бора была далее развита А. Зоммерфельдом, который доказал, что при отыскании стационарных состояний должны учитываться не только круговые, но и эллиптические орбиты, а также и и пространственная ориентация, которой орбиты могут приобретать в магнитном поле. Все это привело к введению в теорию новых квантовых чисел. Те же квантовые числа, что и в теории Бора - Зоммерфельда, но в другом толковании достаем при определении стационарных состояний в квантовой механике.
Для энергетических уровней ионов расчеты проведены с учетом эллиптичности орбит, как и расчеты, основанные на квантовой механике, дают формулу, которая совпадает по формуле:
где n - главное квантовое число, которое определяет размеры орбиты. От этого числа зависит главным образом энергия электрона в атоме. Оно может приобретать только целочисленных значений (n = 1, 2, 3,...).
Согласно теории Бора, которая ограничивалась случаем круговых орбит, момент импульса L электрона в атоме определяется только главным квантовым числом:
В теории Бора - Зоммерфельда, которая учитывает возможность эллиптических орбит, момент импульса электрона также является величине, кратной h(2π), т.е. элементарному момента импульса, но его значение определяется уже не главным квантовым числом л, а другим квантовым числом l, которое называют орбитальным, побочным, или азимутальной.
33. Квантовая механика. Основные положения квантовой механики: квантование энергии, корпускулярно-волновой характер движения микрочастиц, вероятностный метод описания микрообъектов.
Квантовая механика – теория, устанавливающая способ описания и законы движения микрочастиц в заданных внешних полях. Создана в 1924-1926 гг. (Луи де Бройль, Э. Шредингер, В. Гейзенберг и П. Дирак). Важнейшую роль в ее подготовке и развитии имели исследования М. Планка, А. Эйнштейна, Н. Бора, М. Борна и других ученых.
Квантовая (движение микрообъектов) и классическая механика (движение макрообъектов) используют общие принципы: законы сохранения энергии, массы, заряда и импульса. В отличие от классической, квантовая механика основывается на представлении о квантовании энергии, волновом характере движения микрочастиц и вероятностном (статистическом) методе описания микрообъектов.
Корпускулярно-волновые свойства микрочастиц. Явление фотоэффекта (А.Г. Столетов, 1889 г.), заключающееся в выбивании электронов с поверхности металлов, показало, что свет является потоком частиц-фотонов (корпускулярное свойство). С другой стороны, интерференция света (наложение световых волн) и дифракция (рассеяние световых лучей, проходящих через дифракционную решетку) свидетельствуют о волновых свойствах света.
Квантовая механика имеет статистический характер. Она не позволяет определить местонахождение частицы в пространстве или траекторию, по которой движется частица. С помощью волновой функции можно лишь предсказать, с какой вероятностью частица может быть обнаружена в различных точках пространства.
На первый взгляд может показаться, что квантовая механика дает менее точное описание движения частицы, чем классическая механика, которая определяет «точно» местоположение и скорость частицы в каждый момент времени. Однако в действительности это не так. Квантовая механика гораздо глубже вскрывает истинное поведение микрочастиц. Она лишь не определяет того, чего нет на самом деле. В применении к микрочастицам понятия определенного местоположения и траектории вообще теряют смысл. Движение по определенной траектории несовместимо с волновыми свойствами, что становится совершенно очевидным, если проанализировать существо опытов по дифракции.
Описание микрообъектов не может быть дано на основе классической механики, в которой нет места корпускулярно-волновому дуализму. Однозначной характеристикой микрочастицы в квантовой механике является волновая функция - величина, позволяющая определить параметры движения в заданных внешних условиях. Математически волновая функция описывает некоторый процесс, периодический во времени и в пространстве, длина волны которого определяется формулой де Бройля. Однако природа этого процесса не имеет аналогов в макромире, сама волновая функция - ненаблюдаемая величина, не имеющая физического смысла. В квантовой механике с ней связывают так называемые «волны вероятности», так как квадрат амплитуды волной функции является мерой вероятности обнаружения микрочастицы в какой-либо области пространства. Хотя основное уравнение квантовой механики позволяет однозначно определить зависимость волновой функции от координаты и времени в определенных условиях движения микрообъекта, оно фиксирует связь не осуществившихся событий, а потенциальных возможностей этих событий и выражающих их вероятностей. Поэтому однозначная причинно-следственная связь событий, проявляющаяся в классической механике, не свойственна микромиру, здесь эта связь включает и необходимое, и случайное. Даже зная начальное состояние и условия движения микрообъекта, невозможно однозначно предсказать его последующее поведение. Описание его состояния с помощью волновой функции отражает изначально присущую микрообъектом вероятностность поведения. Не наглядность создаваемых квантовой механикой моделей микромира не противоречит объективности даваемых ею знаний, но отражает качественное отличие свойств объектов микро- и макромира |
|
|
 Скачать 489.52 Kb.
Скачать 489.52 Kb.