Основное свойство дроби. Книга для учителя. М. Просвещение, 2002. Примерные программы по учебным предметам. Математика. 56 классы. М. Просвещение, 2010
 Скачать 0.55 Mb. Скачать 0.55 Mb.
|
|
Методическая разработка урока математики в 6 классе с использованием инновационных средств обучения «ОСНОВНОЕ СВОЙСТВО ДРОБИ» Учебно-методический комплекс: Используемая литература 1. Манвелов С.Г. Конструирование современного урока математики. Книга для учителя. – М.: Просвещение, 2002. 2. Примерные программы по учебным предметам. Математика. 5–6 классы. – М.: Просвещение, 2010. 3. Альхова З.Н., Макеева А.В. Внеклассная работа по математике. – Саратов: Лицей, 2002 4. Головкина В.В. Подведение итогов урока. Рефлексия. Статья. http://ezhva-licey.ru/teachers/nmr/metodich_razrabotki/itogi_uroka/ 5. Виленкин Н.Я., Математика, учебник для 6 класса. Используемые сайты Единая коллекция цифровых образовательных ресурсов. http://school-collection.edu.ru/ Открытый класс: сетевые образовательные сообщества. http://www.openclass.ru/ 2020 Цель Формирование у учащихся знания основного свойства дроби и умения его использовать при преобразовании дробей. Основное содержание темы, термины и понятия Основное свойство дроби, понятие приведения дроби к новому знаменателю, понятие сокращения дроби, сравнение с половиной. Планируемые результаты Личностные -развитие мотивов учебной деятельности; -развитие умения не создавать конфликтов и находить выходы из спорных ситуаций. Метапредметные Познавательные: -приобретение опыта исследовательской деятельности, развития идей, постановки и формулирования новых задач. Регулятивные: -развитие навыков критического мышления, готовности к самообразованию. Коммуникативные: -развитие коммуникативных навыков групповой деятельности; приобретение опыта творческой деятельности и учебного сотрудничества в достижении общепоставленной цели. Предметные В познавательной (интеллектуальной) сфере: умение применять основное свойство дроби при преобразовании дробей. В ценностно-ориентационной сфере: использование приобретенных знаний для устной прикидки и оценки результата сравнения. В сфере физической деятельности: умение изображать дроби точками на координатном луче. Организация образовательного пространства Традиционное оборудование: индивидуальные карточки с изображениями кругов и координатного луча, цветные карандаши, наборы из 20 цветных квадратиков для групповой работы, карточки для диагностики качества освоения темы, анкеты для рефлексии. Инновационное оборудование Компьютер, проектор, экран (или интерактивная доска). Электронные ресурсы: Основное свойство дроби. Презентация. http://www.openclass.ru/sites/default/files/dig_resource/2010/03/_pptx_94085.pptx Математический диктант. Сокращение дробей. Презентация. http://school-collection.edu.ru/catalog/res/ea59f0b2-5030-413b-b3cc-da6970430d5b/view/ Основное свойство дроби. Задание для проверки. http://files.school-collection.edu.ru/dlrstore/64ad9368-18b6-4972-ab17-78ca06f03096/%5BM56_6-01%5D_%5BQS_06-02%5D.html Межпредметные связи: История. Формы работы: Фронтальная, индивидуальная, работа в паре, в группе. ТЕХНОЛОГИЯ ИЗУЧЕНИЯ ТЕМЫ Этап I Самоопределение к деятельности (целеполагание) Цель Подведение обучающихся к постановке новой учебной задачи. Ситуативное задание (на экране) Выполните действия 2/7 + 3/7 13/15 – 11/15 8/9 + 4/9 1 – 3/4 10/16 + 3/8 Сравните: 3/16 и 7/16 5/6 и 5/9 15/15 и 2/2 7/8 и 8/7 2/3 и 11/18 Форма работы: Выполняя данные задания, ученики используют правила: сложение и вычитание дробей с одинаковыми знаменателями; сравнение дробей с одинаковыми знаменателями; сравнение дробей с одинаковыми числителями; сравнение правильных и неправильных дробей. Но в ходе решения последних заданий возникает проблемная ситуация — ученики осознают несоответствие между тем, что знают и умеют, и требованием задачи. Ученикам предлагается сформулировать суть возникшего противоречия и способ его устранения. Учитель. Итак, тема урока «Основное свойство дроби». Ребята, попытайтесь обозначить тот круг вопросов, который обычно возникает при изучении нового учебного материала. А я запишу ваши вопросы на доске. Ожидаемый ответ: В чем смысл основного свойства дроби? Каким образом это свойство позволит выйти из создавшейся проблемной ситуации? Существует ли математическая запись этого свойства? Какие операции можно выполнять с дробями, зная основное свойство дроби? Этап II Изучение нового материала Цель Формулирование основного свойства дроби через постановку перед обучающимися учебной проблемы. Задание 1 Докажите, что дроби 1/2, 2/4, 4/8 выражают одну и ту же величину, а, следовательно, они равны. Для этого: И  зобразите данные дроби на координатном луче, выбрав удобный единичный отрезок зобразите данные дроби на координатном луче, выбрав удобный единичный отрезок Закрасьте часть круга, соответствующую каждой из данных дробей 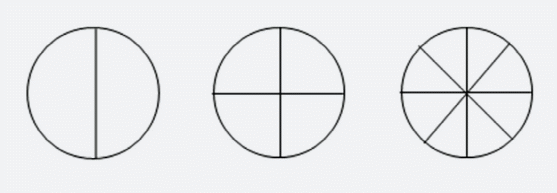 Форма работы: Ученики с помощью цветных карандашей выполняют задание на карточках, приготовленных учителем, и на основании проделанной работы ими делается вывод: полученные дроби оказались равны, т.к. на координатном луче точки совпали, а части всех трех кругов совпадают. Запись на доске и в тетрадях учеников: 1/2 = 2/4 = 4/8. Учитель. Ребята, приведите свои примеры дробей, равных 1/2. Ученики с места дают ответы. Учитель. Сравнивать дроби, используя прием приведения их к общему знаменателю, люди научились гораздо позже, а до этого они пользовались многими другими способами, которые также приводили их к правильному ответу. Например, сравнение с половиной. Задание 2 Выясните, что больше, 3/8 или 5/9. Ожидаемый ответ: если эти дроби сравнивать с 1/2 (половиной), то 3/8 меньше 1/2, а 5/9 больше 1/2. Значит, 5/9 > 3/8. Задание 3 Основное свойство дроби. Презентация. Слайды 4—8. http://www.openclass.ru/sites/default/files/dig_resource/2010/03/_pptx_94085.pptx Из 20 цветных квадратиков, среди которых 8 розовых, 4 зеленых, 5 желтых и 3 синих, размером 3 см ×3 см, составьте прямоугольник из 4 рядов, распределив цвета произвольным образом. Учитель. Какая часть фигуры закрашена желтым цветом? Ожидаемый ответ: 5/20 Как найти площадь желтой части фигуры, если площадь всей фигуры 16 мм2? Ожидаемый ответ: 16 : 20 · 5 Подумайте, как можно расположить в прямоугольнике желтые квадратики, чтобы в решении задачи использовалась другая дробь, по значению равная 5/20? При этом ответ можно было бы получить без сведения промежуточного результата к десятичной дроби. В создавшейся проблемной ситуации рождается идея: желтые квадратики нужно расположить в один ряд, и тогда желтым цветом закрашена 1/4 часть фигуры. 16 : 4 · 1=4 (мм2) Учитель. Какая часть фигуры закрашена зеленым цветом? Ожидаемый ответ: 4/20. Как найти площадь зеленой части фигуры, если площадь всей фигуры 15 мм2? Ученики догадываются, что зеленые квадратики нужно расположить в один столбик, и тогда зеленым цветом закрашена 1/5 часть фигуры. 15 : 5 · 1=3 (мм2) Учитель. Какая часть фигуры закрашена розовым цветом? Ожидаемый ответ: 8/20. Как найти площадь розовой части фигуры, если площадь всей фигуры 25мм2? Для ответа на вопрос розовые квадратики нужно расположить в два столбика, и тогда розовым цветом закрашены 2/5 части фигуры. 25 : 5 · 2 = 10 (мм2) Учитель. Подумайте, как из дроби 5/20 получить дробь 1/4? А как из дроби 1/4 снова получить 5/20? Ученики, находясь в процессе открытия нового знания, приходят к выводу, что в первом случае это происходит при делении числителя и знаменателя дроби 5/20 на 5, во втором случае — при умножении числителя и знаменателя дроби 1/4 на 5. Запись на доске и в тетрадях учеников a/b = ac/bc, c ≠ 0. Этап III Этап усвоения и закрепления новых знаний. Цель Вовлечь обучающихся в процесс формирования навыков правильного воспроизведения своих знаний и установить степень усвоения темы «Основное свойство дроби». Задание Математический диктант. Сокращение дробей. Презентация. Слайды 1, 3. http://school-collection.edu.ru/catalog/res/ea59f0b2-5030-413b-b3cc-da6970430d5b/view/ 1 вариант Представьте дробь 18/27 со знаменателем 3. Среди дробей 6/10, 9/10, 21/35, 21/40 выберите те, которые равны 3/5. 2 вариант Представьте дробь 20/25 со знаменателем 5. Среди дробей 9/12, 9/16, 18/24, 15/24 выберите те, которые равны 3/4. Ученики имеют возможность провести самопроверку на основе ответов, представленных на слайде и оценить свою работу на данном этапе урока. Отметка выставляется исходя из следующих критериев: «3», если правильно выполнено 3 задания; «4», если правильно выполнено 4 задания; «5», если правильно выполнены все задания. Учитель. Ребята, обратимся к записи на доске, сделанной мной вначале занятия – это тот круг вопросов, который был обозначен вами по теме урока: В чем смысл основного свойства дроби? Каким образом это свойство позволит выйти из создавшейся проблемной ситуации? Существует ли математическая запись этого свойства? Какие операции можно выполнять с дробями, зная основное свойство дроби? Удалось ли нам в полной мере раскрыть эти вопросы? Проверим. Задание 1 Основное свойство дроби. Презентация. Слайд 11. http://www.openclass.ru/sites/default/files/dig_resource/2010/03/_pptx_94085.pptx Расставьте математические термины число, дробь, знаменатель, равная, разделить, числитель, умножить по местам, заполнив пропуски. Если ___________ и _____________ дроби _________ или __________ на одно и тоже натуральное _______ , то получится __________ ей _________ . Задание 2 Умножьте числитель и знаменатель указанной мной дроби на 5: 1/5, 3/7, 25/8, 39/40. Запишите результаты. Задание 3 Разделите числитель и знаменатель указанной мной дроби на 3: 6/3, 9/6, 15/9, 21/33. Запишите результаты. Ученики на предложенных карточках выполняют задание, после чего карточки сдаются учителю на проверку. Учитель. Итак, сколько операций с обыкновенной дробью мы можем выполнить, чтобы получить равную ей дробь? Ожидаемый ответ: Можно умножить числитель и знаменатель дроби на одно и то же число, не равное нулю, а можно разделить. Учитель. При умножении числителя и знаменателя на одно и то же число мы приводим дробь к новому знаменателю. Возвращаясь к заданиям, вызвавшим у вас затруднения, 10/16 + 3/8 подумайте и скажите, на какое число нужно умножить числитель и знаменатель дроби 3/8, чтобы слагаемые стали с одинаковыми знаменателями? 2/3 и 11/18 На какое число нужно умножить числитель и знаменатель дроби 2/3, чтобы сравниваемые дроби стали с одинаковыми знаменателями? Ожидаемый ответ: в первом случае – на 2, тогда 10/16 + 6/16 = 16/16 = 1, а во втором случае – на 6, тогда 12/18 >11/18. Историческая справка: «Не есть се дивно, что в целых, но есть похвально, что в долях», — говорили раньше. К общему знаменателю дроби приводили уже в шестнадцатом веке, а складывать дроби научились только в семнадцатом веке. Наука о дробях долгое время была одна из самых запутанных. У немцев до сих пор сохранилась поговорка: «Попасть в дроби», что значит, не найти выхода из создавшегося положения. Того, кто не знал дробей, не признавали сведущим в математике. При делении числителя и знаменателя дроби на одно и то же число, не равное нулю, мы выполняем операцию, которая называется сокращением дроби. Но это тема следующего урока. Этап VI Рефлексивная деятельность Цель Подключение обучающихся к оценке результатов своей работы на уроке. Учитель. В конце урока я предлагаю каждому из вас заполнить небольшую анкету, которая позволит дать качественную и количественную оценку нашему уроку. 1. На уроке я работал 2. Своей работой на уроке я 3. Урок для меня показался 4. За урок я 5. Мое настроение 6. Материал урока мне был активно / пассивно доволен / не доволен коротким / длинным не устал / устал стало лучше / стало хуже понятен / не понятен полезен / бесполезен интересен / скучен Этап V Домашняя задание: Задание для проверки по теме «Основное свойство дроби». http://files.school-collection.edu.ru/dlrstore/64ad9368-18b6-4972-ab17-78ca06f03096/%5BM56_6-01%5D_%5BQS_06-02%5D.html Задание из учебника: п.8, № 237,240. В электронных дневниках учеников указывается ссылка на нужный сайт. Задание №1 из домашней работы по теме «Основное свойство дроби». http://files.school-collection.edu.ru/dlrstore/64ad9368-18b6-4972-ab17-78ca06f03096/%5BM56_6-01%5D_%5BQS_06-02%5D.html Используя основное свойство дроби, сократите дробь 30/288 на 6, сделав подробную запись: 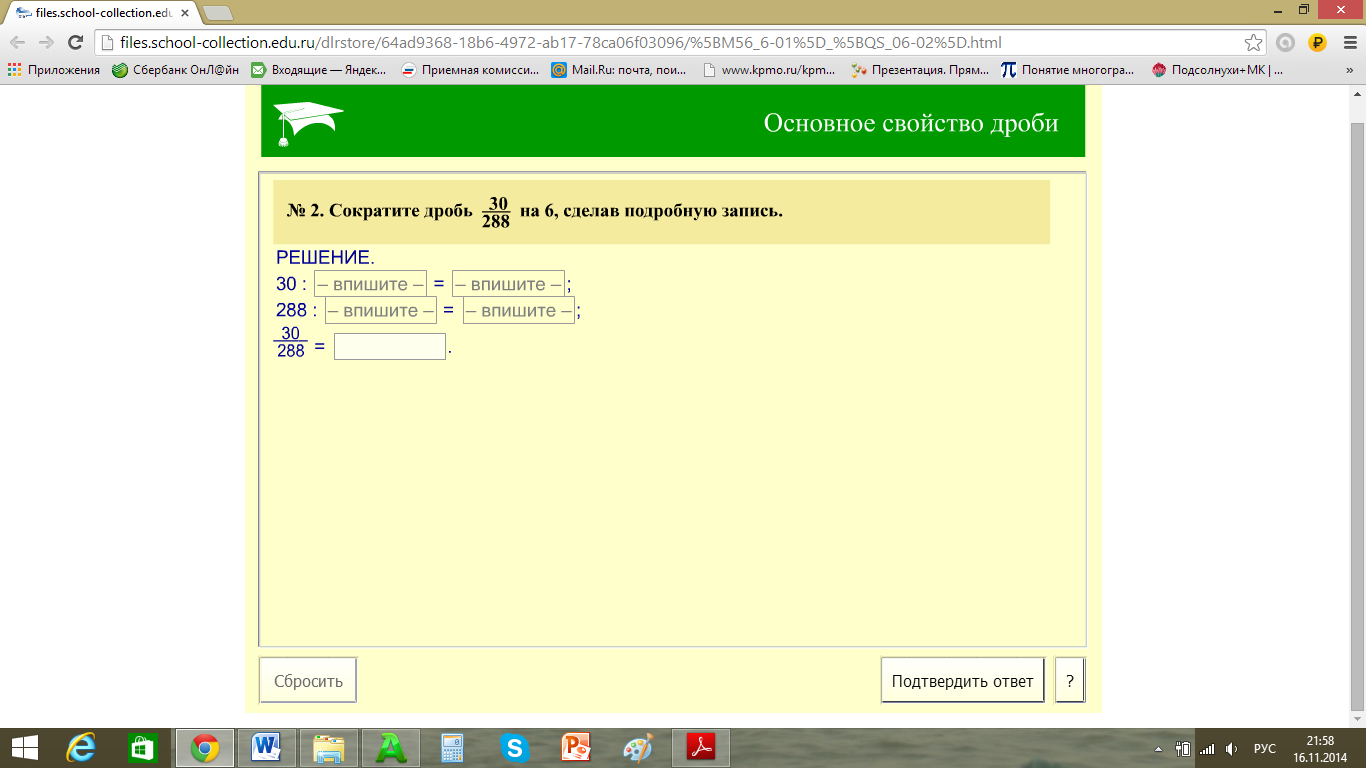 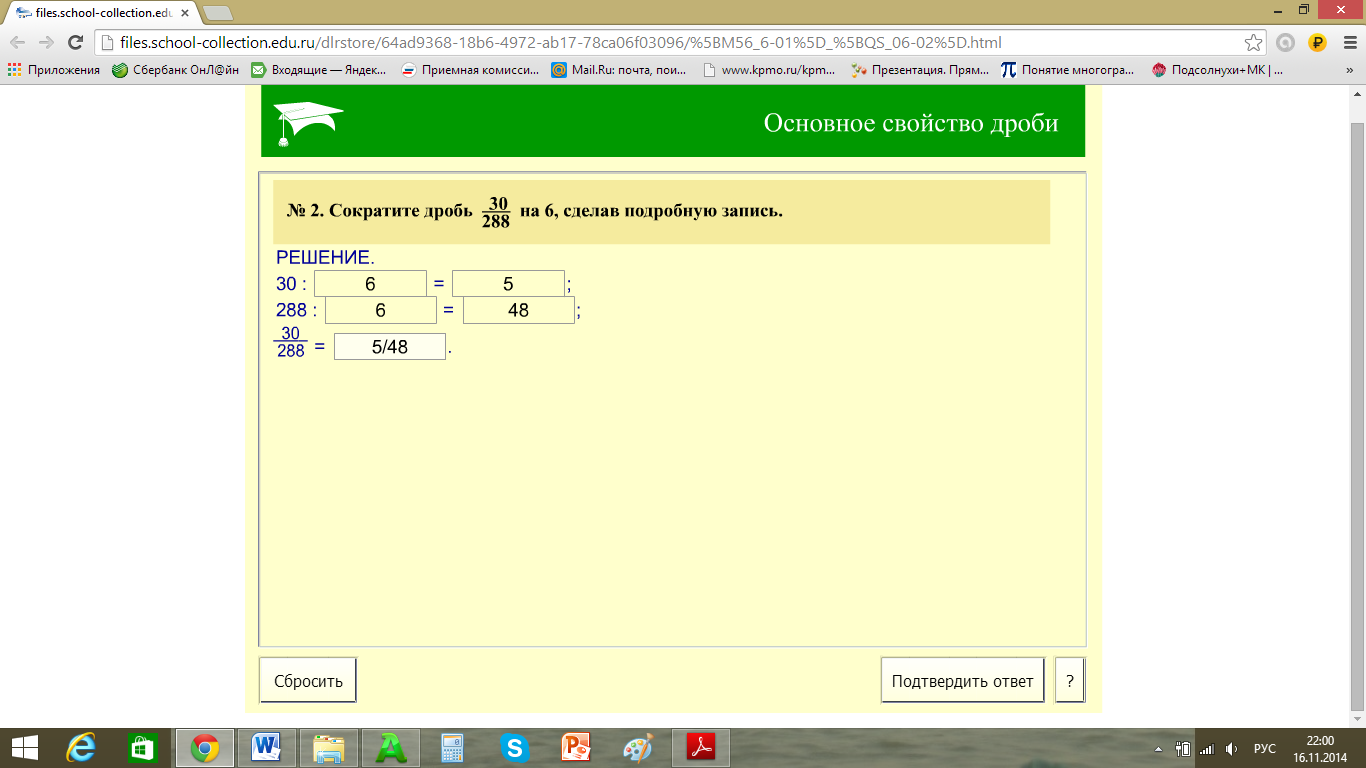  Выполняя предложенное интерактивное задание, ученики видят результаты своих действий – правильный шаг отмечается зеленым цветом, а неверный – оранжевым. Если задание в целом выполнено не верно, они получают нужные рекомендации и могут выполнить задание повторно. Данное задание нацеливает обучающихся на успешное освоение материала следующего урока «Сокращение дробей». |
