Колебания и волны
 Скачать 1.37 Mb. Скачать 1.37 Mb.
|
|
Министерство образования Российской Федерации ГОУ ВПО Уральский государственный технический университет - УПИ КОЛЕБАНИЯ И ВОЛНЫ Вопросы для программированного теоретического коллоквиума по физике для студентов всех форм обучения всех специальностей Екатеринбург 2003 УДК 530(075.8) Составители М.Г. Валишев, Е.С. Левин, Ф.А. Сидоренко Научный редактор КОЛЕБАНИЯ И ВОЛНЫ: Вопросы для программированного теоретического коллоквиума по физике/ М.Г. Валишев, Е.С. Левин, Ф.А. Сидоренко. Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2003, 40 с. Приведены варианты вопросов для программированного контроля знаний при изучении темы «Колебания и волны». Вопросы соответствуют действующей рабочей программе по физике, могут быть использованы для студентов всех форм обучения всех специальностей. Подготовлено кафедрой физики Рукопись редактирована и подготовлена к изданию с помощью электронных настольных издательских систем в Региональном Центре Новых Информационных Технологий УГТУ-УПИ
ГОУ ВПО Уральский государственный технический университет - УПИ, 2003 КОЛЕБАНИЯ И ВОЛНЫ Вопросы для программированного теоретического коллоквиума по физике, 2003 г. 1.1. Ниже под номерами 2, 4, 8 приведены графики зависимости от смещения Х полной W и потенциальной Wn энергии материальной точки, а под номером 1 – модуль F результирующей силы К 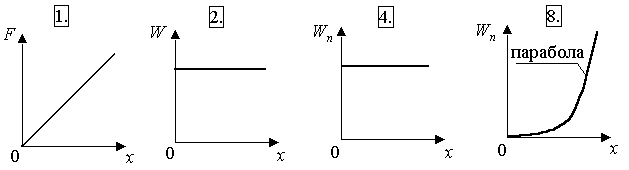 акие графики соответствуют гармоническим колебаниям материальной точки? Укажите сумму их номеров. 1.2. Материальная точка совершает незатухающие гармонические колебания вдоль оси 0х. Для нее считаются известными следующие величины: 1. х – смещение (координата) точки в произвольный момент времени t (х0); 2. ах – проекция на ось 0х ускорения точки в этот же момент времени; 4. W – полная механическая энергия; 8. k – жесткость системы. Выразите массу m материальной точки через эти величины. Какие из них вошли в расчетную формулу? Укажите сумму их номеров. 1 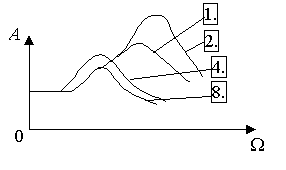 .3. Частица совершает вынужденные колебания в среде с коэффициентом затухания колебаний . Под номером 1 приведен график зависимости амплитуды А вынужденных колебаний частицы от частоты вынуждающей силы. Какой из трех других графиков будет соответствовать зависимости А(), если коэффициент затухания колебаний увеличится? .3. Частица совершает вынужденные колебания в среде с коэффициентом затухания колебаний . Под номером 1 приведен график зависимости амплитуды А вынужденных колебаний частицы от частоты вынуждающей силы. Какой из трех других графиков будет соответствовать зависимости А(), если коэффициент затухания колебаний увеличится?1.4. Уравнение затухающих колебаний материальной точки имеет вид где А0 = 10 см, 0 = 10 рад/с. Чему равен период Т колебаний этой точки, если коэффициент затухания колебаний = 8 с-1? 1.5. Ниже под номерами 1 и 2 изображены траектории результирующего движения, получающегося при сложении двух взаимно перпендикулярных гармонических колебаний, а под номерами 4 и 8 – векторные диаграммы, получаемые при сложении двух гармонических колебаний одного направления и одинаковой частоты с амплитудами А1 и А2 ( Д 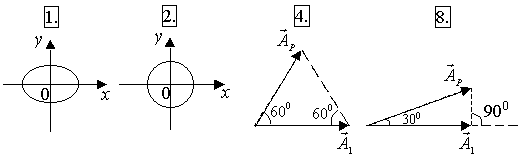 ля таких случаев разность фаз складываемых колебаний равна /2? Укажите сумму их номеров. 1.6. Для каких случаев амплитуды А1 и А2 складываемых колебаний не равны друг другу (рис. из 1.5)? Укажите сумму номеров этих рисунков. 1.7. Найдите максимальную энергию Wэ max электрического поля конденсатора, если максимальное напряжение на конденсаторе колебательного контура Um=80 В, индуктивность контура L = 10-2 Гн, период колебания Т = 210-3 с. сопротивлением контура пренебречь. 1 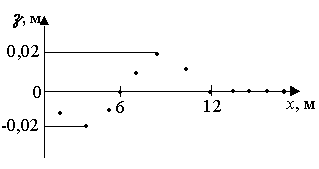 .8. На рис. приведена моментальная «фотография» модели плоской поперечной гармонической волны в момент времени t = 3 с. Источник колебаний находится в точке с координатой Х = 0. В начальный момент времени t = 0 все частицы среды находились в покое. Чему равна (в СИ) скорость V распространения волны? .8. На рис. приведена моментальная «фотография» модели плоской поперечной гармонической волны в момент времени t = 3 с. Источник колебаний находится в точке с координатой Х = 0. В начальный момент времени t = 0 все частицы среды находились в покое. Чему равна (в СИ) скорость V распространения волны?1.9. Чему равна (в СИ) максимальная скорость Vm частиц среды? 1 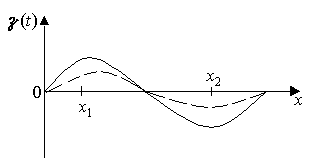 .10. На рис. приведены графики смещения частиц среды в стоячей волне для двух различных моментов времени. .10. На рис. приведены графики смещения частиц среды в стоячей волне для двух различных моментов времени.Чему равна (в СИ) разность фаз колебаний частиц с координатами х1 и х2? 1.11. Ниже под номерами 1, 4 изображены векторы напряженности В 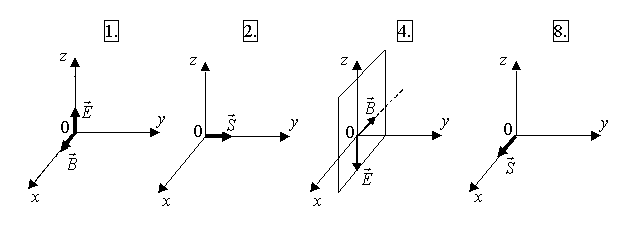 каких случаях электромагнитная волна распространяется в положительном направлении оси 0у? Укажите сумму номеров этих диаграмм. 1.12. В среде распространяется плоская электромагнитная волна. Известны следующие параметры волны и характеристики среды: 1. - диэлектрическая проницаемость среды, 2. - магнитная проницаемость среды, 4. Еm – амплитуда напряженности электрического поля волны, 8. - длина волны в среде. Получите выражение для периода Т волны через приведенные выше величины и константы 0, 0, с. Укажите сумму номеров величин, вошедших в расчетную формулу. 1 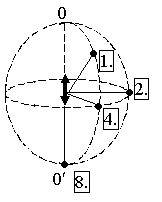 .13. Получите выражение для амплитуды Bm индукции магнитного поля волны через приведенные выше величины и константы 0, 0, с. Какие из обозначенных цифрами величин вошли в расчетную формулу? Укажите сумму их номеров. .13. Получите выражение для амплитуды Bm индукции магнитного поля волны через приведенные выше величины и константы 0, 0, с. Какие из обозначенных цифрами величин вошли в расчетную формулу? Укажите сумму их номеров.1.14. Электрический диполь совершает гармонические колебания вдоль оси 00. Цифрами обозначены различные направления в пространстве. В каких направлениях энергия излучения диполя максимальна? Укажите сумму номеров этих направлений. Составители: М.Г. Валишев, Е.С. Левин, Ф.А. Сидоренко ГОУ ВПО УГТУ-УПИ, Екатеринбург, 2003. КОЛЕБАНИЯ И ВОЛНЫ Вопросы для программированного теоретического коллоквиума по физике, 2003 г. 2  .1. Ниже приведены графики зависимости кинетической Wк и максимальной потенциальной Wп max энергии от времени t при различных видах механических колебаний. Обозначения осей ординат не указаны. Какие графики могут соответствовать зависимости максимальной потенциальной энергии Wп max системы от времени? Укажите сумму их номеров. 2 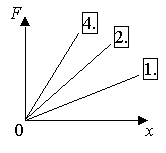 .2. Какие графики могут соответствовать колебаниям, происходящим в консервативной системе? Укажите сумму их номеров. .2. Какие графики могут соответствовать колебаниям, происходящим в консервативной системе? Укажите сумму их номеров.2.3. Материальная точка массой m совершает гармонические колебания. На рис. приведены графики зависимости модуля F квазиупругой силы, действующей на нее, от смещения Х. В каком случае угловая частота гармонических колебаний точки будет наибольшей? 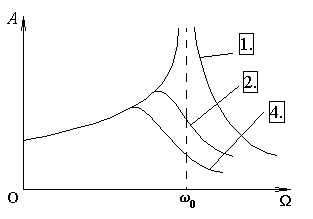 2.4. На рис. приведены графики зависимости амплитуды А вынужденных колебаний от частоты вынуждающей силы для трех систем с номерами 1, 2 и 4. Эти системы имеют различные значения коэффициента затухания колебаний и одинаковую частоту 0 собственных незатухающих колебаний. У какой системы частота затухающих колебаний наименьшая? 2.5. Для какой системы логарифмический декремент затухания æ наибольший? 2.6. Материальная точка участвует в двух взаимно перпендикулярных колебаниях. Траектория ее результирующего движения – окружность радиуса R = 0,05 м. Определите амплитуды А1, А2 и разностью фаз складываемых колебаний. Предположим, что эти же два колебания будут происходить вдоль одного направления с этими же амплитудами А1, А2 и той же разностью фаз . Определите амплитуду Ар получаемого при этом результирующего колебания. 2.7. Колебательный контур состоит из катушки индуктивностью L = 410-4 Гн и конденсатора емкости С = 1610-8 Ф. При каком наименьшем значении сопротивления Rкр контура в нем будет наблюдаться апериодический разряд, т.е. = 0? 2 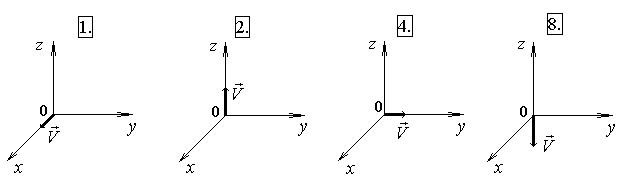 .8. В упругой среде распространяется плоская монохроматическая волна. Ниже под номерами 1, 2 изображены направления вектора скорости В каких случаях колебания частиц среды могут происходить вдоль оси 0у? Укажите сумму номеров этих диаграмм. 2.9. В упругой среде распространяется механическая волна от источника, начинающего совершать незатухающие гармонические колебания в момент времени t = 0. Считаются известными следующие величины: 1. х – расстояние между точкой среды и источником колебаний; 2. t0 – момент начала колебаний этой частицы; 4. Т – период волны; 8. А – амплитуда волны. Через эти величины выразите длину волны . Укажите сумму номеров величин, вошедших в расчетную формулу. 2.10. Через какие из этих величин можно выразить разность фаз колебаний выделенной точки среды и источника колебаний? Укажите сумму их номеров. 2.11. В упругой среде возникла стоячая волна. Верно ли, что… 1. …все частицы среды одновременно проходят положение равновесия? 2. …амплитуда колебаний всех частиц одинакова? 4. …расстояние между соседними пучностями равно /2? 8. …все частицы среды колеблются в одинаковой фазе? На какие вопросы вы ответили «да»? Укажите сумму их номеров. 2.12. Ниже под номерами 1, 4 указаны векторы скорости 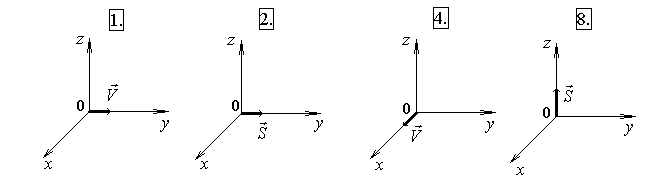 В каких случаях векторы 2 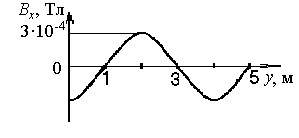 .13. В среде с магнитной проницаемостью = 1 и диэлектрической проницаемостью = 9 в положительном направлении оси 0у распространяется плоская электромагнитная волна. На рис. приведен график зависимости проекции Вх индукции магнитного поля волна на ось 0х от координаты у в произвольный момент времени t. Определите период Т волны. .13. В среде с магнитной проницаемостью = 1 и диэлектрической проницаемостью = 9 в положительном направлении оси 0у распространяется плоская электромагнитная волна. На рис. приведен график зависимости проекции Вх индукции магнитного поля волна на ось 0х от координаты у в произвольный момент времени t. Определите период Т волны.2.14. Определите (в СИ) амплитуду Еm напряженности электрического поля волны. Составители: М.Г. Валишев, Е.С. Левин, Ф.А. Сидоренко ГОУ ВПО УГТУ-УПИ, Екатеринбург, 2003. КОЛЕБАНИЯ И ВОЛНЫ Вопросы для программированного теоретического коллоквиума по физике, 2003 г. 3 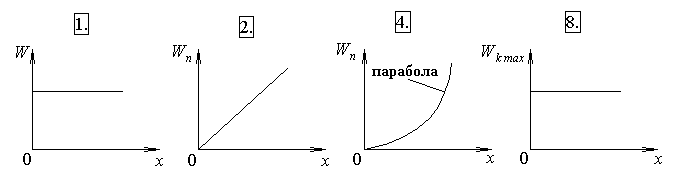 .1. Ниже под номерами 1, 2, 4 приведены графики зависимости полной Wn энергии материальной точки от смещения Х, а под номером 8 – график зависимости максимальной кинетической энергии Wk max от времени t для материальной точки. Какие графики могут соответствовать незатухающим гармоническим колебаниям материальной точки? Укажите сумму их номеров. 3.2. Материальная точка совершает незатухающие гармонические колебания вдоль оси 0х. Для нее в произвольный момент времени t считаются известными следующие величины: 1. х – смещение (координата) (х 0), 2. Vx – проекция скорости на ось 0х, 4. F – модуль результирующей силы, действующей на точку, 8. Wk – кинетическая энергия. Выразите угловую частоту 0 колебаний точки через приведенные выше величины. Какие из них вошли в расчетную формулу? Укажите сумму их номеров. 3.3. Через какие из этих величин можно выразить потенциальную энергию Wn точки в момент времени t. Укажите сумму их номеров. 3 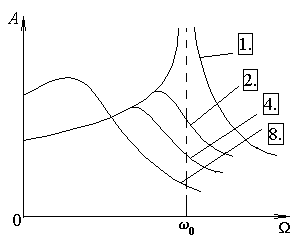 .4. На рис. приведены графики зависимости амплитуды А вынужденных колебаний смещения материальной точки массы m от частоты вынуждающей силы для четырех систем с различными значениями коэффициента затухания колебаний и одинаковой частотой 0 собственных незатухающих колебаний. .4. На рис. приведены графики зависимости амплитуды А вынужденных колебаний смещения материальной точки массы m от частоты вынуждающей силы для четырех систем с различными значениями коэффициента затухания колебаний и одинаковой частотой 0 собственных незатухающих колебаний.В каком случае амплитуда Fm вынуждающей силы максимальна? Для какой системы коэффициент затухания наименьший? Укажите сумму номеров соответствующих графиков. 3 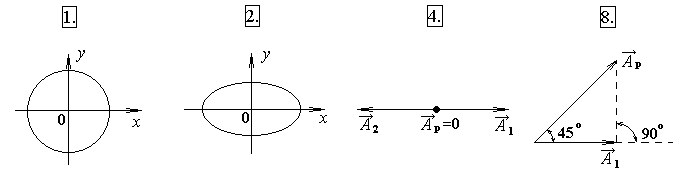 .5. На рисунке под номерами 1, 2 изображены траектории результирующего движения при сложении двух взаимно перпендикулярных гармонических колебаний, а под номерами 4, 8 – векторные диаграммы сложения гармонических колебаний одного направления и одинаковой частоты ( Для каких случаев разность фаз складываемых колебаний равна /2? Укажите сумму их номеров. 3.6. Для каких случаев амплитуды А1 и А2 складываемых колебаний одинаковы? Укажите сумму их номеров. 3.7. Период затухающих колебаний в колебательном контуре равен Т = 1,110-6 с. При каком логарифмическом декременте затухания æ амплитуда Um напряжения на конденсаторе за время t = 10-4 с уменьшится в е раз ( 3 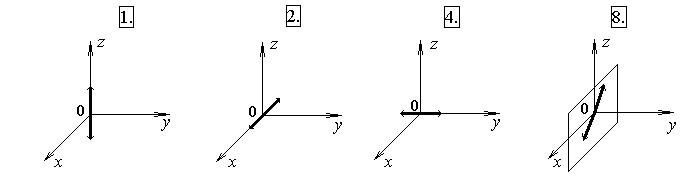 .8. В упругой среде распространяется плоская монохроматическая волна. На рисунке стрелками указаны направления колебаний частиц среды. В каких случаях вектора скорости 3 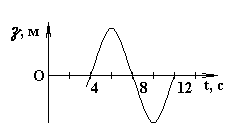 .9. В упругой среде распространяется плоская монохроматическая волна. В начальный момент времени t = 0 все частицы среды находились в покое. На рисунке приведен график зависимости от времени смещения частицы, отстоящей от источника колебаний на расстояние х = 1 м. Чему равны (в СИ) длина волны ? .9. В упругой среде распространяется плоская монохроматическая волна. В начальный момент времени t = 0 все частицы среды находились в покое. На рисунке приведен график зависимости от времени смещения частицы, отстоящей от источника колебаний на расстояние х = 1 м. Чему равны (в СИ) длина волны ?3 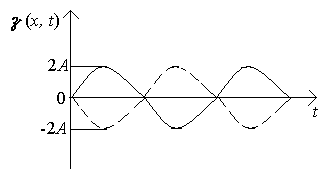 .10. Чему равна (в СИ) разность фаз колебаний частиц среды, отстоящих от источника на расстояниях х1 = 2 м и х2 = 3 м? .10. Чему равна (в СИ) разность фаз колебаний частиц среды, отстоящих от источника на расстояниях х1 = 2 м и х2 = 3 м?3.11. Стоячая волна образовалась наложением бегущей и отраженной волн с длиной волны = 10 м. На рисунке приведены графики зависимости смещения двух частиц среды от времени. Чему равно минимальное расстояние х между этими частицами (А – амплитуда бегущей волны)? 3.12. В среде распространяется плоская электромагнитная волна. Известны следующие параметры волн и характеристики среды: 1. - диэлектрическая проницаемость среды, 2. - магнитная проницаемость среды, 4. - угловая частота волны, 8. Еm – амплитуда напряженности электрического поля волны. Получите выражение для длины волны через приведенные выше величины и константы 0, 0, с. Укажите сумму номеров величин, вошедших в расчетную формулу. 3.13. Получите выражение для амплитудного значения Sm индукции магнитного поля волны через приведенные выше величины и константы 0, 0, с. Какие из обозначенных цифрами величин вошли в расчетную формулу? Укажите сумму их номеров. 3 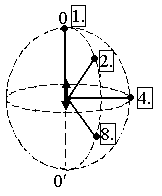 .14. На рисунке изображен электрический диполь, совершающий гармонические колебания вдоль оси 00’. Цифрами обозначены различные направления в пространстве. .14. На рисунке изображен электрический диполь, совершающий гармонические колебания вдоль оси 00’. Цифрами обозначены различные направления в пространстве.В каком направлении диполь не излучает электромагнитных волн? Составители: М.Г. Валишев, Е.С. Левин, Ф.А. Сидоренко ГОУ ВПО УГТУ-УПИ, Екатеринбург, 2003. |
