Комбинаторные задачи как средство развития комбинаторного стиля мышления. комбинаторные задачи. Комбинаторные задачи как средство развития комбинаторного стиля мышления младших школьников
 Скачать 0.65 Mb. Скачать 0.65 Mb.
|
|
Глава 2 Использование комбинаторных задач для развития комбинаторного стиля мышления у младших школьников в процессе обучения математики. 2.1 Основные вопросы в начальном курсе математики. Научить ребенка решению комбинаторных задач нужно так, чтобы каждый ученик решал любую из них с любым сюжетом легко, быстро и правильно. Покажем возможность взаимосвязи комбинаторных задач с содержанием начального курса математики, выделив основные вопросы для каждого класса. 1 класс: Занятия в первом классе начинаются с уточнения представлений детей о признаках (свойствах) предметов. Это позволяет использовать опыт младших школьников и имеющиеся у них математические представления для организации целенаправленного наблюдения, которое включает в себя такие мыслительные операции, как анализ и синтез, сравнение, классификация, обобщение. Целенаправленная работа по формированию приемов умственных действий на первых уроках учитывает, как различный опыт ребенка, так и различный уровень его математической подготовки. В результате этой работы у первоклассников формируются представления о признаках предметов, об их изменении, о расположении в пространстве, об их количестве, которые тесно связаны с операцией счета. На этих же уроках ребенок адаптируется к школьной обстановке, овладевает общеучебными умениями: работать с учебником, слушать учителя и других учеников, принимать участие в обсуждении, работать в тетради и т.д. В первом классе комбинаторные задачи включаются в такие темы: Признаки предметов, Сложение и состав числа, Двухзначные числа. Рассмотрим подробнее работу над данными темами: Признаки предметов Комбинаторные задания органически включаются в общую систему заданий, предлагаемых в учебнике по теме «Признаки предметов» и в то же время имеют свою специфику. Она заключается в том, что, выполняя задания учебника, учащиеся анализируют и сравнивают уже данные совокупности, а при выполнении комбинаторных заданий они сами образуют различные совокупности предметов, отличающиеся друг от друга теми или иными признаками. Причем другие совокупности получаются в результате преобразования данной. Так же важно учитывать то, что задачи построены в игровой форме, с помощью разноцветных карандашей, раскрашивая рисунки, ученик выполняет то или иное упражнение. Например: А) Представь, что у тебя четыре кружки разного цвета, раскрась эти кружки (рис 13).  Рисунок 13 - Решение задачи Б) Ты решил подарить другу две кружки. Покажи на рисунке, какие кружки ты можешь выбрать. Сколько вариантов у тебя получилось (рис. 14)? 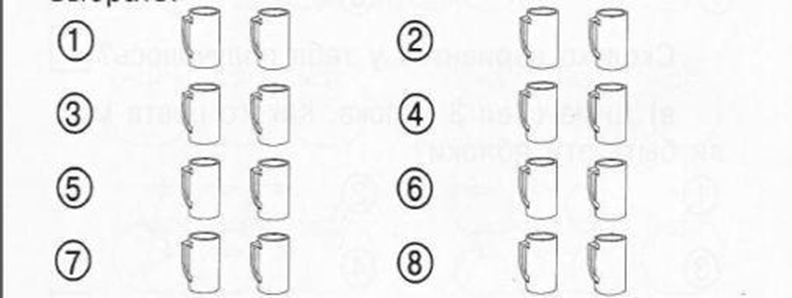 Рисунок 14 - Решение задачи В) А если ты захочешь подарить другу три кружки? Сколько вариантов выбора у тебя будет (рис. 15)? 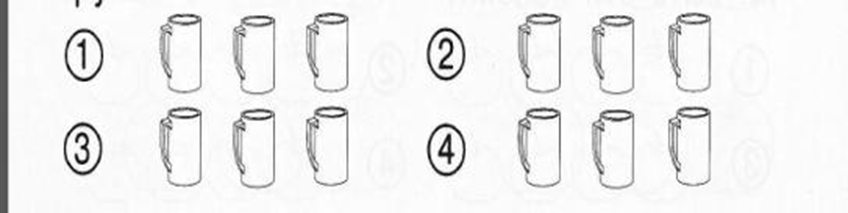 Рисунок 15 - Решение задачи Эти задания можно выполнять практически. Можно поставить на стол четыре кружки разного цвета и вызвать четырех учеников. Все остальные внимательно следят, не допустят ли дети ошибок при выборе кружек. Это задание можно предложить при изучении темы «Признаки предметов», «Число и цифра». Сложение. Состав числа. «Сложение». Основная цель этой темы - разъяснить смысл действия сложения и познакомить младших школьников с той терминологией, которая употребляется в математике при сложении (выражение, сумма, слагаемые, значение суммы, равенство). Основа этого разъяснения - взаимосвязь сложения натуральных чисел с операцией объединения попарно непересекающихся конечных множеств, которая легко интерпретируется на действиях с предметами. Пример: в вазе лежат 6 яблок и 3 груши. Сколько существует возможных вариантов выбора: а) одной груши? 3 варианта б) одного яблока? 6 вариантов в) либо груши, либо яблока? 6+3= 9 Двухзначные числа. При изучении нумерации двухзначных чисел деятельность учащихся направляется на осознание позиционного принципа десятичной системы счисления и на соотношение разрядных единиц. Следует отметить, что комбинаторные задания, связанные с изучением этой темы, включены в различные учебники для начальных классов, однако у многих детей они вызывают затруднения и поэтому чаще всего классифицируются как задания повышенной трудности. Например: «Из цифр 2, 3, 4, 5 составь двузначные числа, чтобы число десятков было больше числа единиц». Исходя из условия задачи, понятно, что не нужно записывать все двузначные числа. Варианты чисел должны быть такими, чтобы первая цифра в их записи была «старшей». «Сколько существует двузначных чисел, сумма числа десятков и единиц которых равна 16?» В задании нужно провести неполный перебор возможных вариантов. Достаточно только выбрать цифры для записи этих чисел (сумма которых дает число 16), а их всего три: 7, 8, 9 Так же могут использоваться такого рода задания: Составь все возможные выражения, расставляя знаки «+» и «-» между числами 3…5…7. Проводится полный перебор вариантов. К концу обучения в 1 классе учащиеся справляются с решением простых комбинаторных задач способом перебора. Эти задачи развивают наблюдательность, внимание и логическую речь учеников. 2 класс: Формируется: навыки чтения, представления о смысле арифметических действий сложения и вычитания, основные мыслительные операции - анализ и синтез, сравнение, умение описывать предметные ситуации и переводить их на язык схем и математических символов, умение чертить, складывать и вычитать отрезки, умение переводить текстовые ситуации в предметные и схематические модели. Понятие текстовой задачи. Структура задачи. Вводится новая форма записи: таблица. Использование таблиц в процессе решения комбинаторных задач помогает младшим школьникам в последовательном поиске всех возможных вариантов. Число объектов, из которых составляются комбинации, остается небольшим, а количество комбинаций - все возможные. Так же составление таблицы служит для удобства, помогает избежать повторения одной и той же комбинации; составить все возможные комбинации и исключить не удовлетворяющие условию. Пример: у тебя 3 шапочки разного цвета: красная, синяя и желтая - и три шарфа такой же расцветки. А) сколько комплектов из шапочки и шарфа разного цвета можно составить? (Шапочки и шарф, входящие в комплект должны быть разного цвета.) Б) заполни таблицу. (Дети самостоятельно указывают в таблице цвет и расположение шапочек и шарфов, как показано в таблице 3) Таблица 3 – Решение задачи.
Заполнив таблицу и исключив комплекты с повторяющимися цветами, можно с легкостью назвать ответ: 6 комплектов. Умение составлять таблицы в процессе решения задач и находить возможные варианты с учетом условия задачи помогает ученикам в решении задач с большим числом объектов. Например: «Для начинки пирогов бабушка приготовила капусту, рыбу, мясо, щавель и землянику. Чтобы пироги были вкусными, она решила смешивать по две начинки. Какие пироги испекла бабушка? (табл. 4)» Решение этой задачи предлагается второклассникам для самостоятельной работы, так как ситуация, описанная в ней, встречается в жизни каждого ребенка и, решая ее, он опирается на свой жизненный опыт Таблица 4 – Решение задачи
В результате составления таблицы мы видим, что всего получилось 25 вариантов начинок. Из данных вариантов мы исключим: а) одинаковые начинки; б) повторяющиеся (в таблице выделены желтым цветом); в) пироги должны быть вкусными. В результате анализа выполнения работы выясняется, что сложных начинок для пирогов у бабушки получилось совсем немного: капуста с рыбой, капуста с мясом и земляника со щавелем. В процессе знакомства с текстовыми задачами второклассники решают комбинаторные задачи, связанные с сочетаниями и размещениями. Поэтому необходимо обратить внимание детей на задачи, в которых важен порядок записи элементов в комбинации (чаще это связано с задачами на составление двузначных, а далее и трехзначных чисел), а в каких нет. Умножение. В теме «Умножение» большое внимание уделяется разъяснению предметного смысла действия умножения, усвоению детьми его определения как сложения одинаковых слагаемых и осознанию ими новой математической записи. Для этой цели в учебнике предложены различные виды упражнений: на выделение признаков сходства и различия данных выражений; на соотнесение рисунка и числового выражения; на запись числового выражения по данному рисунку; на выбор числового выражения, соответствующего рисунку; на замену произведения суммой; на сравнение числовых выражений и т.д. 3. Трехзначные числа. При изучении нумерации трехзначных чисел деятельность учащихся направлена на осознание позиционного принципа десятичной системы счисления. Комбинаторные задачи на размещения органически включаются в данный раздел развивающего курса математики начальной школы, так как при составлении таких комбинаций учитывается порядок в записи ее элементов. Таким образом, в программное содержание второго года обучения математике в систему развивающего обучения четырехлетней начальной школы были включены комбинаторные задачи на перестановки, размещения и сочетания с небольшим числом элементов. Выбор возможных вариантов проводился методом системного перебора и с использованием правила произведения, которое не давалось в явном виде, а использовалось второклассниками проговариванием своих действий в процессе решения комбинаторной задачи. 3 класс: В третьем классе учащиеся знакомятся с новым методом решения комбинаторных задач - дерево возможных вариантов. На примере решения комбинаторных задач младшие школьники знакомятся с графами как способом их решения. Основные вопросы третьего года обучения математике в начальных классах: текстовые задачи на четыре арифметических действия; порядок выполнения действий; действия с четырехзначными, пятизначными и шестизначными числами. Нумерация многозначных чисел в курсе третьего класса представлена темами: «Четырехзначные числа» и «Пятизначные числа». Основными способами усвоения десятичной позиционной системы счисления являются: анализ многозначных чисел с точки зрения их разрядного состава, выявление признаков сходства и различия в конкретных числах, построение рядов чисел в соответствии с определенными правилами. 3. Многозначные числа: (четырехзначные, пятизначные и шестизначные числа). На примере решения комбинаторных задач младшие школьники знакомятся с графами как способом их решения. Пример задачи с четырехзначными числами: «Сколько различных четырехзначных чисел можно записать, используя цифры 6, 5, 2?» Для ответа на вопрос задачи заполни часть схемы дерева возможных вариантов (рис. 16). Так как в условии задачи предложены три цифры, то при записи четырёхзначных чисел цифры будут повторяться. Чисел, в которых 6 тысяч- 27, 5- тысяч- 27, 2 тысячи-27. В итоге мы получаем -81четырехзначное число. 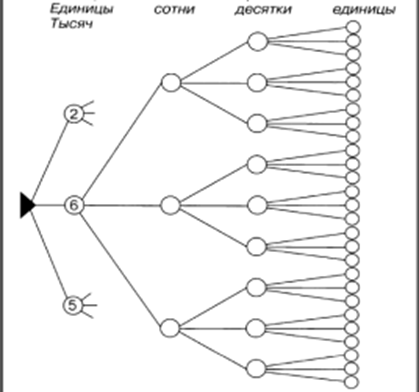 Рисунок 16 - Решение задачи 4 класс. Изучение комбинаторных задач в четвертом классе является повторение и закрепление изученного в третьем классе. Способы решения комбинаторных задач в 3-4 классах: системный перебор с помощью таблиц и правила произведения. Новые способы проведения системного перебора: «граф - дерево» («деревом решений», «деревом возможных вариантов») и линейными графом. 1. Текстовые задачи на четыре арифметических действия, порядок выполнения действий. Способы решения комбинаторных задач в 3-4 классах: системный перебор с помощью таблиц и правила произведения. Новые способы проведения системного перебора: «граф - дерево» («деревом решений», «деревом возможных вариантов») и линейными графом. П 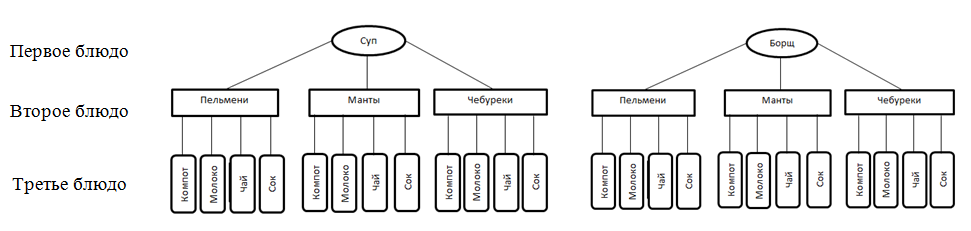 ример: «Сколько различных комплектов обедов из трех блюд можно составить, если в меню есть на первое - борщ и суп, на второе - пельмени, манты, чебуреки, на третье - компот, чай, молоко, сок?» ример: «Сколько различных комплектов обедов из трех блюд можно составить, если в меню есть на первое - борщ и суп, на второе - пельмени, манты, чебуреки, на третье - компот, чай, молоко, сок?»Рисунок 17 - Решение задачи На примере данной задачи целесообразно рассмотреть способа ее решения с помощью «графа-дерева» (рис. 17). Эта работа проводится самостоятельно с проговариванием каждого шага действия. Расставляя точки по количеству блюд каждого вида, и соединяя их отрезками, дети самостоятельно строят «граф-дерево», а затем подсчитывают число возможных комплектов обеда. Комплект из трех блюд можно выбрать – 24 способами. Использование этих способов решения комбинаторных задач целесообразно, когда приходится составлять наборы более чем из 2 элементов. Овладение ими дает возможность решения комбинаторной задачи, т.е. он овладевает навыками самопроверки. Таким образом, в программное содержание третьего и четвертого года обучения математике в системе развивающего включены комбинаторные задачи, связанные с перестановками, размещениями и сочетаниями элементов с большим числом элементов, чем во втором классе. Выбор возможных вариантов осуществляется методом системного перебора с помощью таблиц, графов, «дерева» возможностей и с использованием правила суммы и правила произведения. Органическое включение комбинаторных задач в программное содержание позволяло избежать перегрузки учащихся дополнительной научной информацией. В результате изучения комбинаторных задач в начальных классах ученик должен знать и понимать: Что такое комбинаторная задача и уметь вычленить ее из множества текстовых (арифметических) задач; Способы решения комбинаторных задач. Уметь решать комбинаторные задачи различными способами (перебором, таблицами, дерево возможных вариантов, графами); Использовать полученные знания при решении различных задач, если это возможно. Из этого следует, что возможно научить решать комбинаторные задачи учащихся начальных классов, используя занимательные задачи и интересные задания и тем самым повысить показатели логического и алгоритмического мышления учащихся. Решение комбинаторных задач под силу каждому ученику начальных классах, но при подборе задач должны учитываться возрастные и индивидуальные особенности младших школьников. При обучении комбинаторных задач должна соблюдаться этапность. Комбинаторные задачи, связанные с жизненными ситуациями, смогут повысить показатель логической памяти и гибкости мышления. Связь комбинаторных задач с программным содержанием может повысить эффективность проведения уроков по математики, если их включать систематически, но при этом урок не должен быть перегружен дополнительной информации. Задачи_на_построение_дерева_возможных_вариантов»_Цель'>2.2 Фрагменты уроков Конспект урока по математике для 4 класса на тему «Задачи на построение дерева возможных вариантов» Цель: научиться решать и записывать задачи на построение дерева возможных вариантов. Задачи: Образовательные: Познакомить учащихся с основными приемами подсчета различных вариантов при решении комбинаторных задач; Учить решать комбинаторные задачи с помощью перебора всех возможных вариантов (комбинаций чисел, слов, предметов и др.); Формировать умения моделировать ход решения с помощью рисунка, дерева возможных вариантов. Развивающие: Развивать математическую речь; Развивать умение обобщать, систематизировать, анализировать, сравнивать; Развивать внимание; Развивать логическое мышление; Умение делать выводы. Воспитательные: Воспитывать интерес к изучению математики; Воспитывать самостоятельность; Воспитывать желание преодолевать трудности. Формы работы: фронтальная, самостоятельная работа, самопроверка, работа в парах, взаимопроверка. Формирование УУД: Личностные УУД: Принятие образца «хорошего ученика»; Формирование интереса (мотивации) к учению. Регулятивные УУД: Организовывать свое рабочее место под руководством учителя; Определять цель выполнения заданий на уроке; Волевая саморегуляция; Прогнозирование уровня усвоения; Оценка; Коррекция. Познавательные УУД: Умение осознано строить речевое высказывание в устной форме; Отвечать на простые вопросы учителя; Построение логической цепи рассуждений; Использование индуктивного умозаключения. Коммуникативные УУД: Участвовать в диалоге на уроке; Отвечать на вопросы учителя, товарищей по классу; Слушать и понимать речь других; Ход урока I Мотивация к учебной деятельности Есть о математике молва, Что в порядок ум она приводит, Потому хорошие слова Часто говорят о ней в народе. - Как вы понимаете эти слова? - А что мы с вами приводим в порядок? - Какую тему мы с вами рассмотрели на прошлом уроке? - Что изучает комбинаторика? - Какие способы решения комбинаторных задач вам уже известны? II. Актуализация знаний Понятие, способ действия: - Сегодня на уроке, вы познакомитесь с еще одним способом решения комбинаторных задач. А как он называется вы мне скажите позже, когда решите задачу. Пробное действие: Задача: В школьной столовой на 15.12.20 г. в меню имеются следующие блюда: на первое – суп, борщ, на второе – плов, жаркое, макароны с котлетой, напиток – чай, компот. Сколько можно составить вариантов обеда на сегодня? (Класс делиться на группы, учитель раздает раздаточный материал – карточки с названием блюд). Работа идет фронтально, дети предлагают свои варианты, изображают на доске с помощью наглядности. III Постановка учебной задачи - Опишите задание, которое я вам предлагаю сейчас выполнить? - Является ли оно пробным? - Возникнут ли у вас при выполнении задания затруднения, если да, то какие? Фиксация затруднения: (на доске карточки с формулировками возможных мест затруднений) 1. Не полный перебор блюд. 2. Повторение блюд в меню. Причина затруднения: (ответы учащихся) - Я пока не знаю, как правильно решать задачи такого вида. - Я пока не понимаю, как более рационально (короче) записать решение задач такого вида. Формулировка цели: (ответы учащихся) - Я хочу узнать новый способ решения задач. - Я хочу научиться применять новый способ к решению комбинаторных задач. IV Проблемное объяснение нового знания (вместе с учителем) Изобразите корень дерева, для этого поставьте знак * (или вместо *, можно написать МЕНЮ); Обозначим название блюд первыми буквами их названия: суп – С, борщ – Б, плов – П, жаркое – Ж, макароны с котлетой – МК, чай – Ч, компот – К; Чтобы выбрать первое блюдо, у нас есть два варианта: суп, борщ. Поэтому от корня дерева проведите две ветви (два отрезка) и на их концах поставьте буквы – С, Б; Для выбора второго блюда есть три варианта: плов, жаркое, макароны с котлетой. Поэтому от каждой первой буквы проведем по три отрезка. И на их концах поставьте буквы – П, Ж, МК; Для выбора третьего блюда есть два варианта: чай, компот. Поэтому от каждой второй буквы проведем по два отрезка. И на их концах поставьте буквы – Ч, К; Двигаясь от корня дерева по ветвям, мы получаем всевозможные варианты меню обеда сегодняшнего дня. - На что похожа данная схема? - Как звучит тема урока? - Какую цель ставим перед собой? (ответы учащихся) - На дерево. - (слайд 6) Дерево возможных вариантов. - Научиться решать задачи используя данную схему. Физминутка V Первичное закрепление - Настало время перекусить. Мы идем в школьную столовую Задача. Сколько различных завтраков, состоящих из 1 напитка и 1 вида выпечки, можно составить из чая (ч), кофе (к), булочки (б), печенья (п) и вафель (в)? Заполните схему дерева возможных вариантов в соответствии с условием задачи - Обменяйтесь тетрадями с соседом по парте. Проверьте друг друга. Сколько завтраков у вас должно получиться? (6 завтраков) - Если ваш сосед выполнил задание верно, поставьте «плюс», иначе – «минус». Верните друг другу тетради. VI Самостоятельная работа с взаимопроверкой У детей карточки с заданиями. Выполнить самостоятельно, проверить с другом по парте. Если всё правильно показывают (берутся за руки), если есть ошибки, помогите их друг другу исправить. Не забудьте поблагодарить за помощь. Проверка. Учитель спрашивает 2 -3 х учеников о работе напарника. - Что ты можешь сказать о работе напарника? - Молодцы, ребята. - А где в жизни мы можем столкнуться с решением таких задач? Так ли уж нам нужны эти знания? – Подумайте и приведите примеры. - С чем вы познакомились сегодня на уроке? (с комбинаторными задачами) - Какими способами вы научились решать такие задачи? (перебор, дерево, умножение) - Итак, ученику приходится встречаться с математикой, практически, постоянно. В частности, вы просчитываете различные комбинации – когда? (обсуждение с детьми): когда выбираете меню в столовой, формулируете свой ответ на уроках, составляете график дежурства по классу, планируете, как провести свои выходные или каникулы и так далее. VII. Рефлексия - Ребята, нарисуйте дерево возможных эмоций, которые можно испытывать во время урока, в виде различных смайликов. Закрасьте тот смайлик, который соответствовал вашему настроению на уроке. Конспект урока по математике для 4 класса на тему «Задачи на перебор вариантов» Цель: научиться решать и записывать задачи на перебор вариантов. Задачи: Образовательные: понаблюдать за методом полного перебора вариантов при решении комбинаторных задач; вырабатывать умения применять математическую теорию в конкретных ситуациях; способствовать владению интеллектуальными умениями и мыслительными операциями. Развивающая: формировать умения самостоятельно выбирать способ решения и умения обосновать выбор; формировать умения решать задачи путём логических рассуждений. Воспитательные: воспитывать чувство ответственности за качество и результат выполняемой работы; прививать сознательное отношение к труду; учить работать в парах, в группе, создавать условия для воспитания чувств, взаимовыручки, дружбы. Формы работы: фронтальная, самостоятельная работа, самопроверка, работа в парах, взаимопроверка. В процессе работы формируются: Регулятивные УУД: формировать умение планировать, предвидеть полученный результат, контролировать и оценивать свои действия; умение высказывать свои предположения на основе работы с материалом учебника; принимать и сохранять учебную задачу. Познавательные: выполнять перебор всех возможных вариантов объектов и комбинаций, удовлетворяющих заданным условиям; развивать мыслительную деятельность. Коммуникативные: формировать умение работать в парах, в группе, умение высказывать свои суждения, умение слушать и понимать других; договариваться о совместной деятельности. Личностные: развивать учебно-познавательный интерес к учебному материалу и способам решения задач; ориентировать в нравственных нормах и правилах, вырабатывать свою жизненную позицию. Ход урока I Мотивация к учебной деятельности Сегодня у нас не совсем обычный урок. Садитесь. Ребята, готовы к уроку? На вас надеюсь я, друзья. Мы хороший дружный класс Все получится у нас! А что необходимо для успешной работы? (ответы детей) II Актуализация знаний Начнем работу с устного счета. - Какие из чисел 300, 27, 108, 25, 36, 909, 350, 40, 99, 72, 450, 75 делятся на 5? Делятся на 3, на 2? - Какое число лишнее и почему? 46, 82, 504, 227, 24, 668, 754, 56, 312 - На кормушке сидело 5 воробьёв и 2 синицы. Улетели 3 птицы. Был ли среди них хотя бы один воробей? - Дима моет 4 тарелки за то же время, что и 6 чашек. Что он моет быстрее - тарелку или чашку? - Истинное или ложное высказывание Число 5200 содержит 2 десятка. Неверно, что 10 км 50 м = 1050 м. В марте 31 день и в апреле 31 день. Если 9 * 8 = 72, то 72 : 8 = 9. Тонна – единица длины или скорости. - Придумайте числа, которые делились бы на 2, на 5 и на 8 одновременно. (40, 80, 160, 240, 360…) III Постановка учебной задачи Работа в паре А сейчас я поставлю перед вами задачу. (на столе листочки, на которых записаны цифры 2, 5, 8) Работая в паре, запишите все трёхзначные числа, используя цифры 2, 5, 8 так, чтобы в записи числа цифры не повторялись. Сколько чисел получилось? (спрашиваю несколько человек) Записать на доске (3-5 человек) Кто записал все числа и не пропустил ни одного? Кто испытывал затруднение? В чём? (запутались, повторили числа, некоторые не назвали) Как вы нашли решение этой задачи? (перебирали варианты, записывали те числа, которых ещё не было) Мы учились решать такие задачи? А вы хотите научиться? Значит чему будет посвящен наш урок? (открытию нового знания) Сформулируем тему урока (дети стараются назвать тему урока) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
