Комбинаторные задачи как средство развития комбинаторного стиля мышления. комбинаторные задачи. Комбинаторные задачи как средство развития комбинаторного стиля мышления младших школьников
 Скачать 0.65 Mb. Скачать 0.65 Mb.
|
|
Тема урока «Задачи на перебор вариантов» Чему мы будем учиться на уроке? (Учиться решать и записывать задачи на перебор вариантов) IV Проблемное объяснение нового знания Какая проблема у нас возникла? (не знали, как записать решение) Почему нужно научиться записывать? (чтобы не повторить дважды вариант или не пропустить). Задачи, которые мы сегодня будем решать, в математике ещё называют – комбинаторикой. Найдем определение этого слова в толковом словаре. Комбинаторикой - это раздел математики, посвященный решению задач на перебор различных вариантов, удовлетворяющих каким-либо правилам или условиям. Как вы поняли это определение? (чтобы решить задачи на перебор вариантов нужно знать правило, чтобы их решить) Да, должен быть какой-то способ перебора вариантов. Я предлагаю найти этот способ записи, работая в группе. Вспомните правила работы в группе. Запомни и соблюдай простые правила: 1. Уважай своего товарища. 2. Умей каждого выслушать. 3. Не согласен – предлагай! Подсказка. Вспомним, как мы записываем задачу (условие)? (таблица, схема) Итак, что вы должны сделать? (перебрать всевозможные варианты, придумать определенный способ записи). Папа купил три книги. В каком порядке эти книги можно поставить на книжную полку? (у каждой группы альбомный лист, фломастеры) Ученики каждой группы выходят к доске и рассказывают, как они решали задачу, какой способ записи выбрали. Какой сделаем вывод (при решении задачи лучше сделать таблицу) Сравниваем свой вывод с авторским Физминутка V Первичное закрепление Задача на экране Попробуем применить новое знание на практике. (фронтально) У Васи в тетради нарисован прямоугольник, разделенный на три равные части. Он должен закрасить каждую из этих частей в один из трех цветов: красный, желтый, зеленый. Нельзя окрашивать разные части одинаковым цветом. Сколько вариантов рисунка может получить Вася? (ученик у доски) Работа идет фронтально, дети предлагают свои варианты, изображают на доске с помощью наглядности. Можно ли это задание упорядочить (записать) в таблицу? Как? (заготовки) Как нужно разместить данные в таблицу? VI Самостоятельная работа с взаимопроверкой У детей карточки с заданиями. Выполнить самостоятельно, проверить с другом по парте. Если всё правильно показывают (берутся за руки), если есть ошибки, помогите их друг другу исправить. Не забудьте поблагодарить за помощь. Проверка. Учитель спрашивает 2 -3 х учеников о работе напарника. - Что ты можешь сказать о работе напарника? - Молодцы, ребята. - А где в жизни мы можем столкнуться с решением таких задач? Так ли уж нам нужны эти знания? – Подумайте и приведите примеры. (При составлении расписания уроков, при составлении меню, подбор гардероба, при шифровании и кодировке информации, комбинация грядок с посевами на огороде, на спортивных соревнованиях при расчёте количества игр между командами, комбинации расположения звёзд и планет и т. д.) Задачи на перебор вариантов или комбинаторные задачи играют большую роль в практической деятельности человека. - Я хочу вам предложить решить ещё одну задачу данного вида и записать решение в тетрадь. - Как вы будите записывать решение? (С помощью таблицы.) - В субботу по расписанию три урока: Математика, Русский язык, Литературное чтение. Сколько можно составить вариантов расписания на день? - Проверим. (самопроверка) VII Итог урока. Рефлексия - Какую цель мы ставили на уроке (Учиться решать и записывать задачи на перебор вариантов) Мы научились записывать задачи на перебор вариантов? - Какой способ мы использовали? Закончите предложения Я сегодня узнал(а) … Я научился(лась)… Мне было интересно … Я понял(а), что … Мне было трудно … Материал урока мне … Свою работу я оцениваю … Оценки за урок Спасибо вам, ребята, за работу. Конспект урока по математике для 4 класса на тему «Задачи на размещения» Цель: научиться решать и записывать задачи на размещения. Задачи: Образовательные: Ознакомить с типом задач на размещения, сформировать у учеников первичные умения и навыки решения задач. вырабатывать умения применять математическую теорию в конкретных ситуациях; способствовать владению интеллектуальными умениями и мыслительными операциями. Развивающие: развивать познавательный интерес учеников, логическое мышление, умение применять знания. делать выводы и обобщения. развивать умения сравнивать, систематизировать, обобщать; навыки контроля и самоконтроля. Воспитательные: формировать культуру математической речи, информационную и коммуникативную культуру; воспитание дружелюбного отношения друг другу, умение работать в коллективе. Формы работы: фронтальная, самостоятельная работа, самопроверка, работа в парах, взаимопроверка. В процессе работы формируются: Регулятивные УУД: формировать умение планировать, предвидеть полученный результат, контролировать и оценивать свои действия; умение высказывать свои предположения на основе работы с материалом учебника; принимать и сохранять учебную задачу. Познавательные: выполнять размещение всех возможных вариантов объектов и комбинаций, удовлетворяющих заданным условиям; развивать мыслительную деятельность. Коммуникативные: формировать умение работать в парах, в группе, умение высказывать свои суждения, умение слушать и понимать других; договариваться о совместной деятельности. Личностные: развивать учебно-познавательный интерес к учебному материалу и способам решения задач; ориентировать в нравственных нормах и правилах, вырабатывать свою жизненную позицию. Ход урока I Мотивация к учебной деятельности Я рада приветствовать всех Вас на сегодняшнем уроке. Все мы с вами пришли на урок с разным настроением, но я надеюсь, что в конце нашего занятия у нас у всех будут только положительные эмоции. II Актуализация знаний Актуализация знаний, умений и навыков Прежде чем перейти к изучению нового материала, проведем небольшую разминку по ранее изученному материалу. -Какие числа называются натуральными? - Натуральные числа - это числа, получаемые при счете. - Приведите примеры натуральных чисел. - 1, 4,17,……. - Каким свойством обладают натуральные числа? - Каждое последующее натуральное число больше предыдущего на единицу. - Назовите предыдущее и последующее число для 7, 12, 4, 1, 0 - 6 и 8; 11 и 13; 3 и 5; 2; 0 не является натуральным числом III Постановка учебной задачи Устный опрос А теперь давайте вспомним все то, что мы изучали на прошлых уроках: 1) Какие задачи называются комбинаторными? (Комбинаторная задача – задача, в которой идет речь о тех или иных комбинациях объектов) 2) Может ли комбинаторика помочь в реальной жизни? (обсуждение) Подготовка к активному и сознательному усвоению нового материала Сейчас я предлагаю Вам решить задачу. Туристическая фирма планирует посещение туристами в Италии трех городов: Венеции, Рима и Флоренции. Сколько существует вариантов такого маршрута? ВРФ ВФР РФВ РВФ ФРВ ФВР (6) Запись решения одним из учеников на доске. Тема урока «Задачи на перебор вариантов» Чему мы будем учиться на уроке? (Учиться решать и записывать задачи на размещения) IV Проблемное объяснение нового знания В задачах с размещением без повторения комбинации составляют не из всех элементов заданного множества, а только из некоторых. Но обязательно важен их порядок. Так как элементы в таких задачах повторяться не могут, то мы не можем отобрать больше элементов, чем есть в условии задачи. Особенностью задач на размещение с повторением является то, что возможно выбрать несколько предметов одного вида. Как вы поняли это определение? Я предлагаю найти этот способ записи, работая в группе. Вспомните правила работы в группе. Запомни и соблюдай простые правила: 1. Уважай своего товарища. 2. Умей каждого выслушать. 3. Не согласен – предлагай! Итак, что вы должны сделать? На полке стоят три чашки: желтая, красная и синяя. Мама попросила Машу одну чашку отнести Юле, а другую - Кате. Сколькими способами Маша может это сделать?». Решение данной задачи показано на рисунке 3. Ученики каждой группы выходят к доске и рассказывают, как они решали задачу, какой способ записи выбрали. Какой сделаем вывод. Физминутка. V Первичное закрепление - Как вы считаете, применяется ли комбинаторика на Олимпийских играх? -Сегодня мы и узнаем, где возможно применение комбинаторики на Олимпийских играх. -Рассмотрим флаг России. Из каких цветов состоит российский флаг?(белый, синий, красный). В каком порядке идут эти цвета? 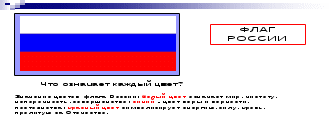 -Что означает каждый цвет? (обсуждение). -Значение цветов флага России: белый цвет означает мир, чистоту, непорочность, совершенство; синий – цвет веры и верности, постоянства; красный цвет символизирует энергию, силу, кровь, пролитую за Отечество. -Оказывается, есть государства, где флаги имеют такие же цвета.  Как подсчитать, сколько таких флагов мы можем составить из трех цветных полосок? VI Самостоятельная работа с взаимопроверкой У детей карточки с заданиями. Выполнить самостоятельно, проверить с другом по парте. Если всё правильно показывают (берутся за руки), если есть ошибки, помогите их друг другу исправить. Не забудьте поблагодарить за помощь. Проверка. Учитель спрашивает 2 -3 х учеников о работе напарника. - Я хочу вам предложить решить ещё одну задачу данного вида и записать решение в тетрадь. - Как вы будите записывать решение? Для конькобежного спорта отведено 5 дорожек. Сколькими способами можно расставить на них 5 спортсменов? 3 спортсмена? Рефлексия. -Проанализируйте свою деятельность на уроке (на отдельных листочках учащиеся пишут одну из трех фраз): -Мне все удалось. -Мне не все удалось, придется дома подольше посидеть. -Мне было очень трудно. Я ничего не понял. Оценки за урок Спасибо вам, ребята, за работу. В начальном обучении математике роль комбинаторных задач постоянно возрастает, поскольку в них заложены большие возможности не только для развития мышления учащихся, но и для подготовки учащихся к решению проблем, возникающих в повседневной жизни. Комбинаторные задачи, составленные на жизненном материале, помогают младшим школьникам лучше ориентироваться в окружающем мире, учат рассматривать все имеющиеся возможности и делать оптимальный выбор. В тоже время применение изучаемых знаний и умений при решении комбинаторных задач позволяет совершенствовать программный материал в процессе его использования в новых условиях. Заключение Исследуя тему «Комбинаторные задачи как средство развития комбинаторного стиля мышления» проанализировали научно-методическую литературу, определили понятие гибкости мышления учащихся младших классов. Так же изучили методику ознакомления учащихся с задачами на комбинаторику. Разработаны фрагменты уроков. Цель исследования выполнена – изучили методику обучения решению комбинаторных задач и развитие комбинаторного мышления у младших школьников. Гипотеза, положенная в основу исследования подтверждается – возможно сформировать первоначальное представление о вероятности и научить решать комбинаторные задачи учащихся младших классов, используя методы проблемного обучения, занимательные задачи. На основе изученной мной литературы можно сказать, что комбинаторные задачи органично вписываются в программное содержание курса математики, их можно решать на уроках математики и связывать с темой урока, не перегружая дополнительной информацией. Также комбинаторные задачи можно использовать во внеурочной деятельности. Анализ учебников математики показал, что комбинаторные задачи встречаются во всех просмотренных мной учебниках, как правило, в учебниках они встречаются в хаотичном порядке и отмечены как задачи «повышенной трудности». Систематичное и регулярное использование комбинаторных задач на уроках математики повысит эффективность учебного процесса. С помощью комбинаторных задач, ученики научатся самостоятельно находить пути решения различных проблем, научатся рассуждать четко, логично и последовательно. При решении комбинаторных задач формируются такие мыслительные процессы, как анализ, синтез, сравнение, классификация, абстрагирование. Решение комбинаторных задач способствуют развитию логического и критического мышления. Решение комбинаторных задач способствует развитию индивидуальных качеств мышления, в том числе такого качества гибкость, вариативность, изобретательность. Комбинаторные задачи должны подбираться с учетом возрастных особенностей учащихся, методы решения комбинаторных задач вводятся по нарастающей траектории от простого к сложному. В начальной школе комбинаторные задачи решаются без использования специальных формул, то есть неформальными методами и рассматриваются 3 вида комбинаций: размещение, сочетания и перестановки. Методы решения комбинаторных задач в начальной школе: Формальный Неформальный, который включает в себя: прием перебора (подбираются задачи на развитие мышления); табличный (все условия вносятся в таблицу, в ней же выполняется решение); 3.построение дерева возможных вариантов решений; построение граф-схемы. В первом и во втором классе комбинаторные задачи решаются методом перебора и при помощи таблиц, в третьем классе ученики строят дерево возможных вариантов и граф - схемы, что дает возможность использовать знакомые способы решения и понятия при изучении некоторых элементов теории вероятности в средней и основной школе. Таким образом, решение комбинаторных задач позволяет расширить знания младших школьниках о видах задач и способах их решений на основе использования различных моделей: таблицы, граф – схемы, дерева возможных вариантов. Включение таких задач в учебный процесс необходимо для лучшего усвоения программных знаний и умений, которые применяются в новых условиях при решении комбинаторных задач, а также помогут ученикам в решении жизненных ситуаций, при построении моделей для поиска вариантов их решения. Список использованных источников. Асмолов, А.Г. Учебное пособие по теме «Формирование УУД» [Текст] / Москва: Просвещение, 2010. – 152 с. Бычкова, Л.О. Об изучении вероятностей и статистики в школе [Текст] // Бычкова Л.О., Селютин В.Д. Математика в школе. – 1991. –№6. С.9 – 12. Белокурова Е. Е. Характеристика комбинированных задач// Начальная школа. 1994. № 1. С. 34-38. Воробьева, С.И. Элементы стохастики в начальной школе (методическая разработка для студентов педфаков). [Текст] / М.: Изд-во МПУ, 1998. – 72с. Выготский, Л.C. Педагогическая психология [Текст] / Под ред. В.В.Давыдова.- М., 2009. – 479 с. Выготский, Л.C. Педагогическая психология [Текст] / Под ред. В.В.Давыдова.- М., 2009. – 479 с. Виноградова Е.П. Учимся решать комбинаторные задачи. М.: Изд-во Ассоциация 21 век, 2011г, 48 с. Воробьева Галина Васильевна Пропедевтика изучения элементов стохаистики на уроках математики в начальных классах [Текст] / Воробьева Г.В. // Педагогическая практика. – 2015. – №4. – С. 70. Гилфорд Д. П. Природа человеческого интеллекта. М., 1971. 3. Якиманская И. С. Развитие пространственного мышления школьников. М., 1980. Комбинаторное мышление [Электронный ресурс] – Режим доступа: http://atbook.km.ru/news/000525.html, свободный (дата обращения 15.04.2021). Комбинаторные задачи в начальном курсе математики [Электронный ресурс] – Режим доступа: https://cyberleninka.ru/article/n/kombinatornye-zadachi-v-nachalnom-kurse-matematiki, свободный (дата обращения 12.03.2021). Левин А., Что такое комбинаторика. //"Квант" [Электронный ресурс]: Физико-математический журнал.-стр.2 Математика и информатика: Учимся решать комбинаторные задачи. Тетрадь для 1-2 классов общеобразовательных учреждений / Н.Б.Истомина, Е.П.Виноградова – 9-е изд. – Смоленск: Ассоциации XXI век, 2013. – 48 с.: ил. Моро М. И. Волкова С. И. Степанова С. В. Математика. Комплект учебников для 1,2,3 и 4 классов.- М.:Просвещение, 2002. Моро М. И., Пышкало А. М. Методика обучения математике в 1-3 классах: Пособие для учителя.- 2-е изд., перераб. и доп.-М.: Просвещение, 1978.-336с Н.Б.Истомина., Е.П.Виноградова., Редько З.Б. Учимся решать комбинаторные задачи. Тетрадь по математике для учащихся 3 класса. – Смоленск: Ассоциации XXI век, 2004. – 48 с.: ил. Ногалес, К «Комбинаторное мышление» / К. Ногалес // 4brain.ru: [сайт]. – 2016 – 28 дек. – URL: https://4brain.ru/blog/комбинаторное-мышление/ (дата обращения: 23.02.2021) Позднякова Н. В. Формирование комбинаторного стиля мышления младших школьников на уроках математики // Дошкольное и начальное образование. Тамбов, 2015. С. 81-87. Проценко, Е. А. Методические аспекты обучения младших школьников комбинаторике / Е. А. Проценко, Ю. В. Трофименко. — Текст : непосредственный // Молодой ученый. — 2014. — № 8 (67). — С. 864-867. — URL: https://moluch.ru/archive/67/11446/ (дата обращения: 08.02.2021). Плоцки, А. Вероятность в задачах для школьников [Текст] // Просвещение Москва. – 1996. –192с. Румянцева И. Б., Муравьева Е. Б., Целищева С. С. Интегрированные комбинаторные задания для младших школьников // Начальная школа. 2014. № 7. С. 97-98. Столяр, A.A. Педагогика математики. [Текст] // Курс лекций. Минск, «Высшая школа», 1969. – 368 с. Тонких, А. П. Стохастика в начальной школе. Сборник задач: пособие для учителей начальных классов [Текст] /А.П. Тонких. – Баласс. – 2010. – 128с Федеральный Государственный Образовательный Стандарт Начального Общего Образования Энциклопедический словарь юного математика // Сост. А.П. Савин. – М.: Педагогика, 1989. – 352 с. Элементы стохаистики в курсе математики начальной школы: Учебно-методическое пособие для учителей начальных классов, учителей математики/Авт.-сост.:тГ.Н.Хорева. – Хабаровск: ХК ИППК ПК, 2007. – 42с. Хорева Галина Владимировна, Обучение решению комбинаторны задач как средство повышения качества математического образования младших школьников [Текст]. - УДК 152.32. Якиманская И. С. Развитие пространственного мышления школьников. М., 1980 Приложения. Приложение 1. Анкета для учителей начальных классов. АНКЕТА ДЛЯ УЧИТЕЛЕЙ НАЧАЛЬНЫХ КЛАССОВ № 1 Комбинаторные задачи в начальном курсе математики Пожалуйста, коротко о себе: Место работы....................................................................................................... Стаж работы в школе.......................................................................................... Занимаемая должность........................................................................................ По какому УМК Вы работаете на уроках математики?……..…………… ……………………….…………………….......................................................... Предусмотрено ли вашим УМК решение комбинаторных задач на уроках математики?......................................................................................................... Используете ли вы комбинаторные задачи во внеурочной деятельности?...................................................................................................... Какие затруднения Вы испытываете в своей работе по данной теме?..................................................................................................................... Какие методы решения усваиваются учащимися, на Ваш взгляд, наиболее легко...................................................................................................................... ............................................................................................................................... Вызывают затруднения................................................................................... .................……………………………………………………………………….. По каким проблемам, темам, вопросам, связанным с преподаванием комбинаторики, Вы захотели бы получить ответ?.......................................... ………………………………………………………...………………………… |
