|
|
Методичка часть 1. Комитет российской федерации по рыболовству
Лабораторная работа №2. «Работа в Electronics Workbench. Основы имитации цифровых устройств. Элементарные логические функции. Логический синтез вычислительных схем».
1. Цель работы:
1.1. Познакомиться с работой в программе Electronics Workbench, а также с элементами, требуемыми для работы с логическими и цифровыми схемами.
1.1. Изучить элементарные логические операции.
1.2. Изучить законы алгебры логики.
1.3. Научиться синтезировать вычислительные схемы устройств.
Изучить и проверить основные тождества алгебры логики.
2. Общие сведения.
Electronics Workbench представляет собой программное обеспечение для имитации процессов, происходящих в электронных схемах. Electronics Workbench позволяет имитировать работу как аналоговых, так и цифровых электронных схем.
Основное окно программы включает в себя главное меню, панели с наборами элементов схем и окно для сборки электронной схемы. В правом верхнем углу находится выключатель для запуска процесса имитации.
На рис. 4.1. представлены основные приборы (панель Instruments), используемые при работе со схемами цифровых устройств. Это Word Generator (Генератор слов) и Logic Analyzer (Логический анализатор).
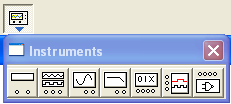
Word Generator
(Генератор слов)

Logic Analyzer
(Логический анализатор)
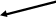
Рис. 4.1. Инструменты «Electronics Workbench».
Выходы (1-16)
 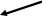
1
16
а) условное обозначение на схеме;
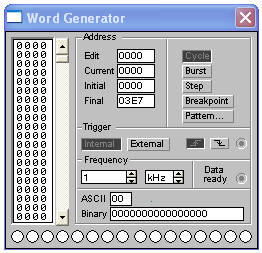
б) Основное окно
Рис. 4.2. Генератор слов.
Настройка генератора слов. Левая часть основного окна генератора слов (поле со полосой прокрутки) представляет собой набор из четырехзначных шестнадцатеричных чисел. Диапазон значений этих чисел от 0000 до FFFF (от 0 до 65535 в десятичной системе счисления), максимальное количество чисел в наборе 999. При активизации генератора шестнадцатеричное число побитно передаётся на соответствующие выходы.
Для изменения последовательности битов подаваемых на выходы генератора можно использовать несколько вариантов:
набрать шестнадцатизначный двоичный код числа в строке «Binary» (это автоматически изменит шестнадцатеричный код, отображаемый в строках левой части генератора);
изменить шестнадцатеричный код, отображаемый в строках левой части генератора;
в строке «ASCII» записать соответствующий ASCII символ.
Управление выходом генератора. Для того чтобы обеспечить повторение подаваемых на выход генератора слов необходимо «зациклить» генератор, включив опцию «Cycle» в поле «Address». Включение опции «Step» обеспечить пошаговую подачу слов на выход генератора при каждом нажатии на кнопку «Step».
Адресация в генераторе слов. Каждое слово в окне генератора имеет свой уникальный адрес, соответствующий шестнадцатеричному номеру из диапазона 000 до 3E7. При вводе или редактировании какой-либо строки в поле «Address» отображается её характеристики, а именно:
«Edit» - адрес слова, на котором стоит указатель;
«Current» - адрес редактируемого в данный момент слова;
«Initial» - адрес, которого начинается подача слов на выход генератора при его запуске;
«Final» - адрес, которым заканчивается подача слов на выход генератора при его запуске.
Частота следования слов для генератора. Частота следования слов изменяется с помощью поля «Frequency». Каждое последующее слово в режиме «Cycle» подается на выход генератора по истечении одного периода следования.
Оставшиеся элементы управления и функции генератора в работах не используются, поэтому студентам предлагается самостоятельное их изучение.
Логический анализатор, представленный на рис. 4.3, используется для отображения уровней логических сигналов и их изменения во времени.
 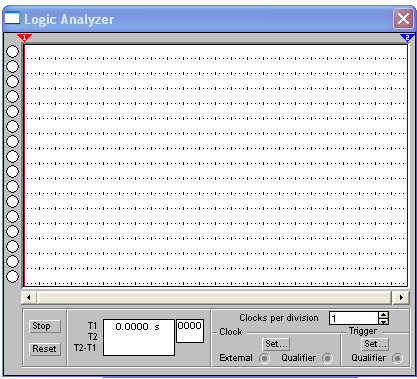
а) условное обозначение б) основное окно.
на схеме;
Рис. 4.3. Логический анализатор.
Red Probe
(логический пробник)
Seven-Segment Display
(Семисегментный индикатор)
Decoded Seven-Segment Display
(Семисегментный индикатор с дешифратором)
Рис. 4.4. Индикаторы «Electronics Workbench».
На рис. 4.4. показаны основные индикаторы, используемые при построении цифровых схем.
К ним относятся:
- Red Probe (RP - Логический пробник)
- Seven-Segment Display (SSD - Семисегментный индикатор)
- Decoded Seven-Segment Display (DSSD - Семисегментный индикатор с дешифратором)
 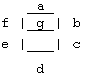 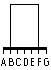 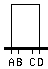
а) RP; б) SSD; в) DSSD.
Рис. 4.5. Условные обозначения индикаторов на схеме.
Логический пробник, показанный на рис. 4.5 (а), представляет собой LED индикатор, который загорается при подаче на его вход логической «1». Пробник может быть использован для индикации «высокого» и «низкого» уровня сигналов в цифровых схемах, а также для графического отображения работы различных счетчиков.
Семисегментный индикатор, показанный на рис. 4.5 (б), отображает состояние своих входов, т.е. при подаче на один из входов логической «1» загорается соответствующий сегмент.
Семисегментный индикатор с дешифратором, показанный на рис. 4.5 (в), проще в использовании по сравнению с семисегментным индикатором, так как каждое шестнадцатеричное число (от 0 до 9 и от A до F) отображается, когда на входы поступает его двоичный код.
Алгебра логики – это раздел математической логики, значение всех элементов (функций и аргументов) которой определены в двухэлементном множестве: 0 и 1. Алгебра логики оперирует с логическими высказываниями.
Высказывание – это любое предложение, в отношении которого имеет смысл утверждение о его истинности или ложности. При этом считается, что высказывание удовлетворяет закону исключенного третьего, т.е. каждое высказывание или истинно или ложно. Одновременно истинным и ложным или НЕ истинным и НЕ ложным оно быть не может.
Простейшими операциями в алгебре логики являются операции логического сложения (ИЛИ, OR, операция дизъюнкции) и логического умножения (И, AND, операция конъюнкции). Для обозначения дизъюнкции используют символы + или V, а конъюнкции – или Λ. Правила выполнения операций в алгебре логики определяются рядом аксиом, теорем и следствий. В частности, для алгебры логики применимы следующие законы.
Сочетательный:
(a + b) + c = a + (b + c),
(a ּ b) ּ c = a ּ (b ּ c).
Переместительный
(a + b) = (b + a),
(a ּ b) = (b ּ a).
Распределительный
a ּ (b + c) = a ּ b + a ּ c,
(a+ּ b) ּ c = a ּ c + b ּ c.
Также справедливы соотношения:
a + a = a, a + b = b, если a ≤ b,
a ּ a = a, a ּ b = a, если a ≤ b,
a + a ּ b = a, a ּ b = b, если a ≥ b,
a + b = a, если a ≥ b,
a + b = b, если a ≤ b,
Наименьшим элементом алгебры логики является 0, наибольшим – 1. В алгебре логики также вводится еще одна операция – отрицания (НЕ, инверсия), обозначаемая чертой над элементом.
По определению:
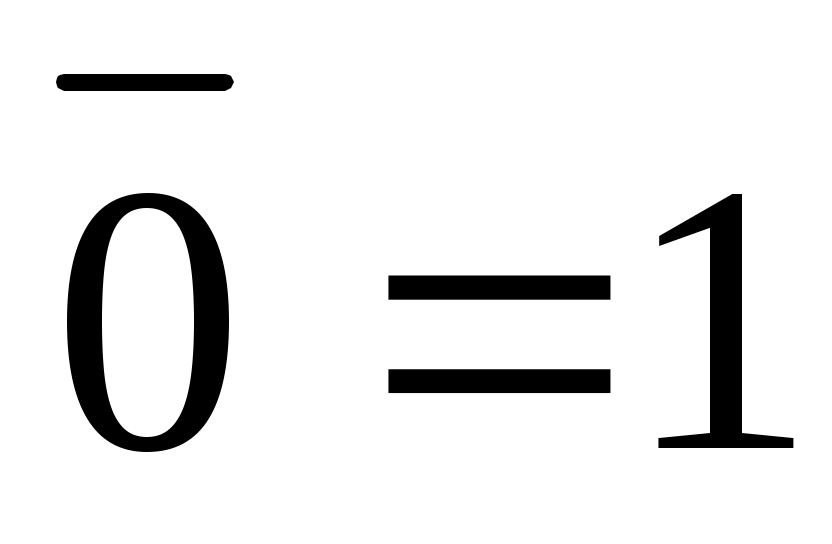 , , 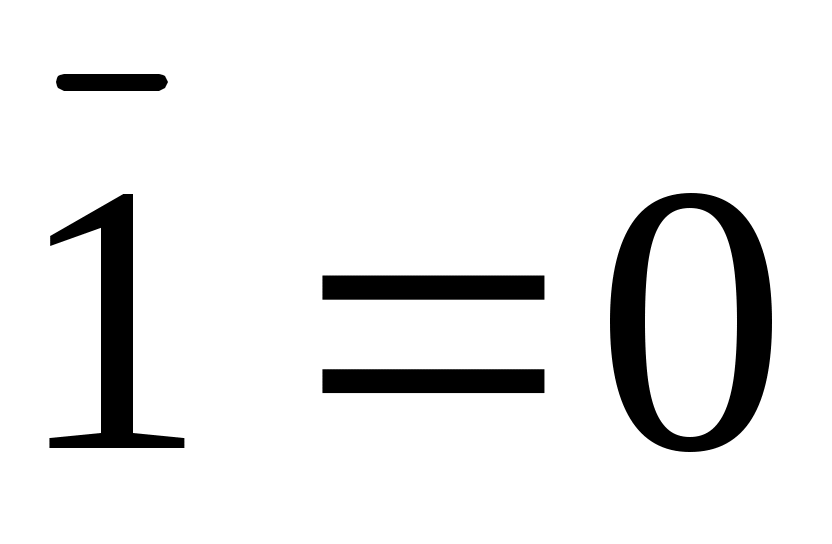 - операция отрицания - операция отрицания
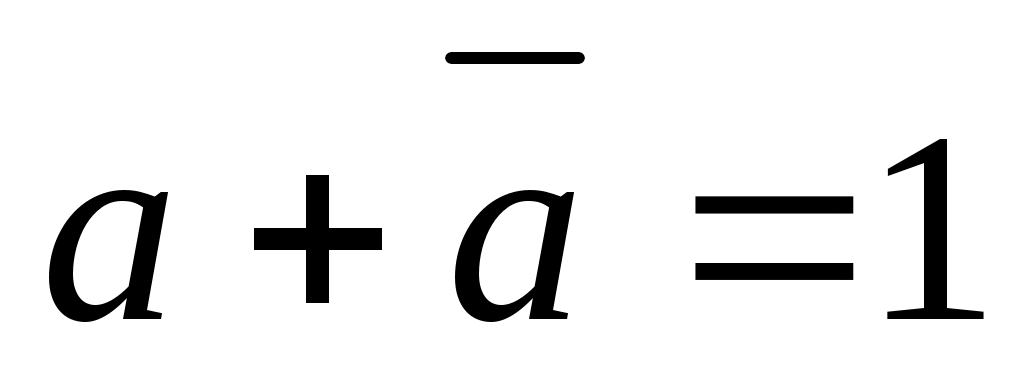 - закон дополнения - закон дополнения
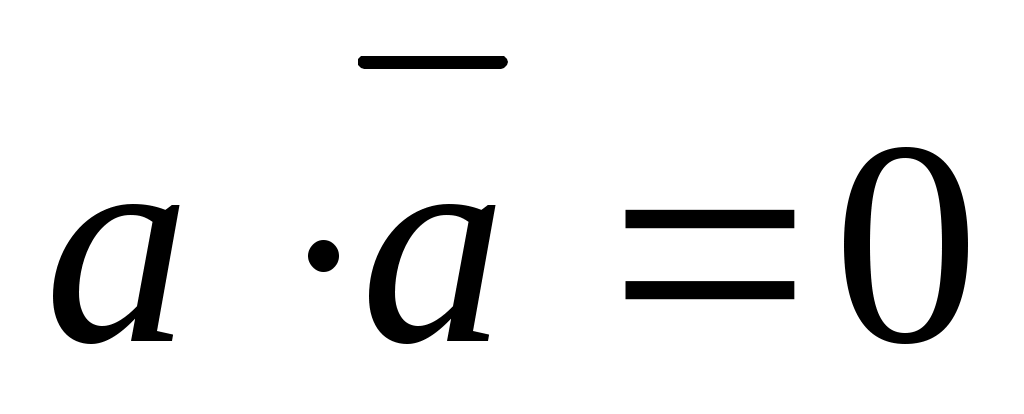 - закон противоречивости - закон противоречивости
Кроме того, справедливы такие соотношения:
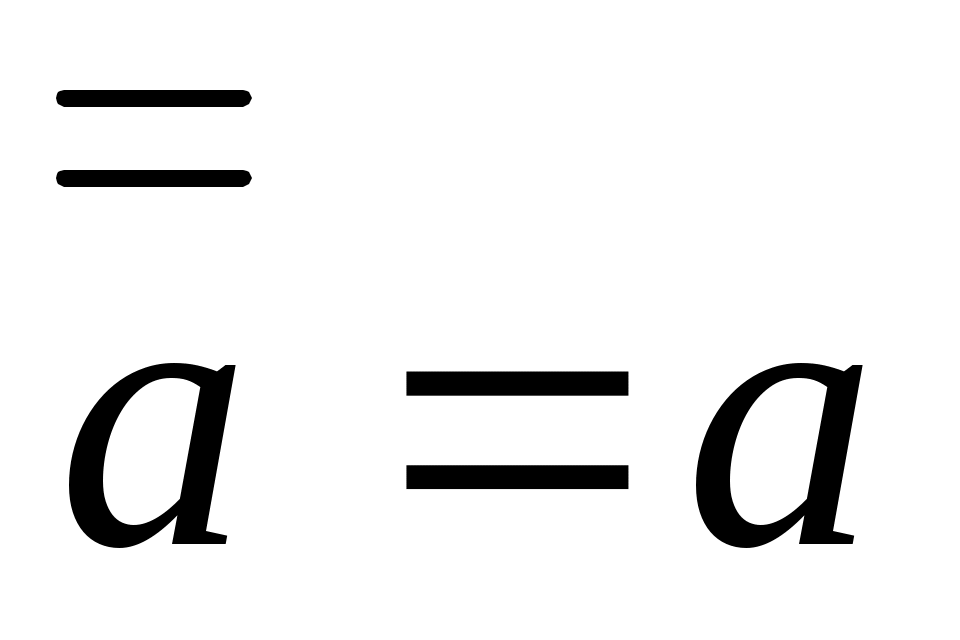 - закон двойного отрицания - закон двойного отрицания
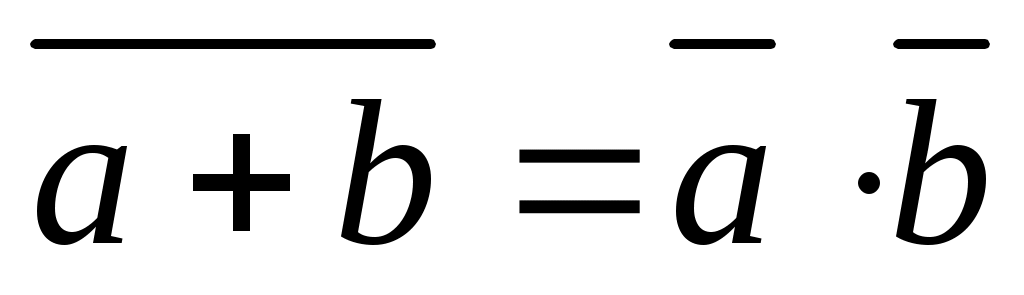 , , 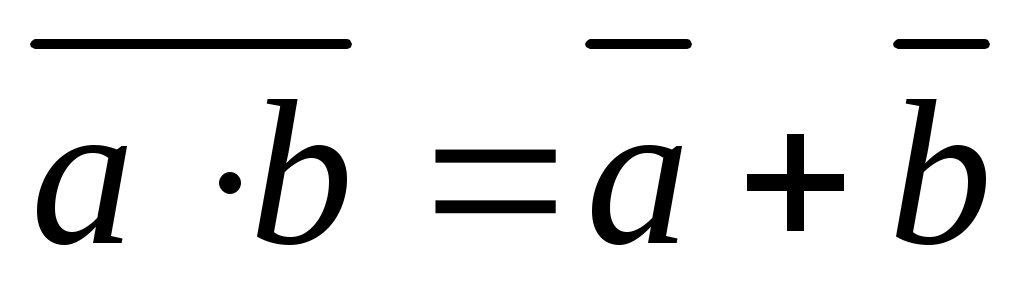 - закон де Моргана - закон де Моргана
Функция в алгебре логики – выражение, содержащее элементы алгебры логики a, b, c и др., связанные операциями, определенными в этой алгебре.
Пример логической функции:
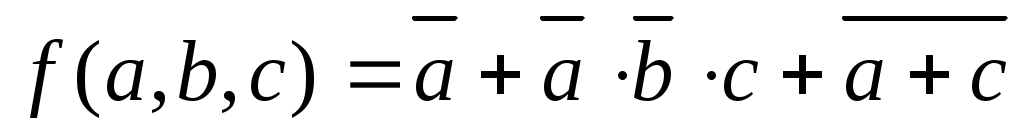
Согласно теоремам разложения функций на конституэнты (составляющие), любая функция может быть разложена на конституэнты 1 и 0:
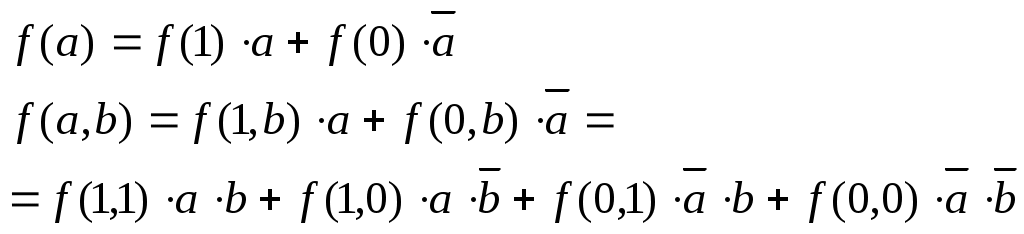 (3.1) (3.1)
Эти соотношения используются для синтеза логических функций и вычислительных схем.
Логический синтез вычислительных схем. В качестве примера рассмотрим синтез одноразрядного двоичного полусумматора, имеющего два входа (a, b) и два выхода (S, P) и выполняющего операцию сложения. Алгоритм работы двоичного полусумматора задан в виде таблице истинности (табл. 3.1). Таблица истинности представляет собой все возможные сочетания входных сигналов и соответствующие им состояния выходных сигналов.
Таблица 3.1. Таблица истинности для синтеза полусумматора.
a
|
b
|
f1(a,b)=S
|
f2(a,b)=P
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
где f1(a,b) = S – значение цифры суммы в данном разряде;
f2(a,b) = Р – цифра переноса в следующий (старший) разряд.
Согласно (3.1), можно произвести разложение на конституэнты:
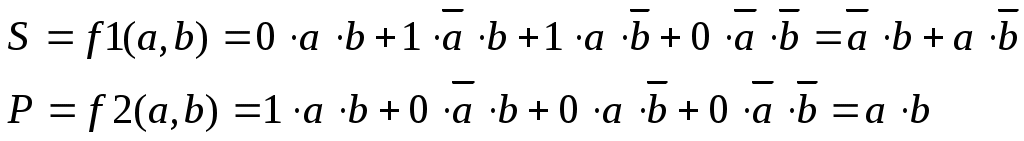
Логическая блок-схема устройства, реализующего полученную функцию, представлена на рис. 3.1. На рис. 3.2. представлены логические блоки, используемые при построении схем в соответствии с международным стандартом и их аналоги согласно ГОСТ. Таблицы истинности наиболее часто используемых в ЭВМ операций представлены в табл. 3.2-3.5.
Операция OR (ИЛИ) – логическое сложение, выполняет поразрядную дизъюнкцию битов двух чисел; устанавливает 1 в тех битах результата, в которых была 1 хотя бы у одного из исходных операндов.
Таблица 3.2. Таблица истинности «ИЛИ».
a
|
0
|
0
|
1
|
1
|
b
|
0
|
1
|
0
|
1
|
a OR b
|
0
|
1
|
1
|
1
|
Операция AND (И) – логическое умножение, выполняет поразрядную конъюнкцию битов двух чисел; устанавливает 1 в тех битах результата, в которых у обоих исходных операндов были 1.
Таблица 3.3. Таблица истинности «И».
a
|
0
|
0
|
1
|
1
|
b
|
0
|
1
|
0
|
1
|
a AND b
|
0
|
0
|
0
|
1
|
Операция XOR (исключающее ИЛИ) – устанавливает 1 в тех битах результата, в которых операнды отличались.
Таблица 3.4. Таблица истинности «исключающее ИЛИ».
a
|
0
|
0
|
1
|
1
|
b
|
0
|
1
|
0
|
1
|
a XOR b
|
0
|
1
|
1
|
0
|
Операция NOT (НЕ) – устанавливает обратное значение битов в числе (инверсия).
Таблица 3.5. Таблица истинности «НЕ».
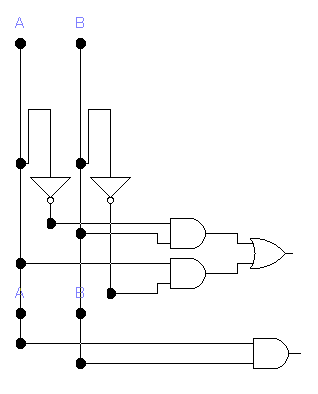
Рис. 3.1. Логическая блок-схема одноразрядного полусумматора.
   
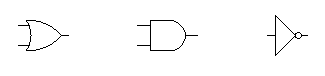
а) «ИЛИ»; б) «И»; в) «НЕ»;
Рис. 3.2. Обозначение логических операций.
При построении логической блок-схемы устройства по некоторой логической функции ее необходимо минимизировать (т.е. упростить) в соответствии с рассмотренными выше соотношениями и законами. Это необходимо для уменьшения стоимости устройств.
Для логических функций «ИЛИ», «И», «НЕ» существуют типовые технические схемы, реализующие их на реле, электронных лампах, дискретных полупроводниковых элементах. Для построения современных ЭВМ применяются системы интегральных элементов, называемые сериями. Для максимальной унификации в качестве базовой логической схемы используется только одна из схем (минимальный базис): «И-НЕ» (NAND, штрих Шеффера), «ИЛИ-НЕ» (NOR, стрелка Пирса) или «И-ИЛИ-НЕ» (NORAND).
В алгебре логики вводится некоторый набор логических аксиом и тождеств.
a(b + c) = ab + ac
a + bc = (a + b)(a + c)
a(a + b) = a
a + ab = a
5) a(not(a) + b) = ab
6) a + not(a)b = a + b
7) ab + a not(b) = a
8) not(ab) = not(a) + not(b)
9) not(a + b) = not(a) not(b)
10) ab + not(a)c + bc = ab + not(a)c
3. Задания для выполнения лабораторной работы.
3.1. Собирать схему (рис.4.6), содержащую цифровой генератор, семисегментный индикатор с дешифратором и четыре логических пробника. Запрограммировать генератор двоичными значениями шестнадцатеричных цифр. В процессе работы схема должна отображать все шестнадцатеричные цифры.
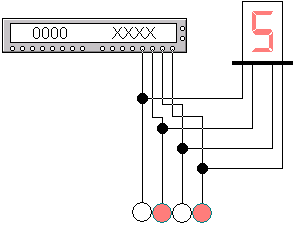
Рис. 4.6. Пример схемы с цифровым генератором.
3.2. Собрать схему, аналогичную предыдущей, с контролем выходов генератора слов с помощью логического анализатора.
3.3. Используя несколько логических пробников, собрать схему «бегущие огни». Варианты исполнения: бегущий огонь влево/вправо, инвертированный бегущий огонь влево/вправо.
3.4. Синтезировать логическую блок-схему устройства, в соответствии с таблицей истинности. Произвести при необходимости минимизацию функции. Варианты заданий для работы приведены в таблице 3.6.
3.5. Путем схемной реализации проверить выполнение всех логических тождеств.
Таблица 3.6. Варианты заданий.
Функция
|
Название функции
|
Х1
|
0
|
0
|
1
|
1
|
Х2
|
0
|
1
|
0
|
1
|
1
|
2
|
3
|
4
|
5
|
6
|
F1= x1 /\ x2
|
Конъюнкция – логическое умножение (И)
|
0
|
0
|
0
|
1
|
F2= x1 \/ x2
|
Дизъюнкция – логическое сложение
|
0
|
1
|
1
|
1
|
F3= x1 → x2
|
Импликация х1 в х2
|
1
|
1
|
0
|
1
|
F4= х1 ← х2
|
Импликация х2 в х1
|
1
|
0
|
1
|
1
|
F5=x1 x2
|
Запрет х2
|
0
|
0
|
1
|
0
|
F6=x1 x2
|
Запрет х1
|
0
|
1
|
0
|
0
|
F7=x1 x2
|
Эквивалентность
|
1
|
0
|
0
|
1
|
F8=x1 x2
|
Сложение по модулю 2
|
0
|
1
|
1
|
0
|
F9=x1/x2
|
И-НЕ – Штрих Шеффера
|
1
|
1
|
1
|
0
|
F10=x1 ↓ x2
|
ИЛИ-НЕ – Стрелка Пирса
|
1
|
0
|
0
|
0
|
F11=x1
|
Повторение х1
|
0
|
0
|
1
|
1
|
F12=x2
|
Повторение х2
|
0
|
1
|
0
|
1
|
F13=1
|
Константа 1
|
1
|
1
|
1
|
1
|
F14=0
|
Константа 0
|
0
|
0
|
0
|
0
|
F15=x1^
|
Инверсия х1- НЕ х1
|
1
|
1
|
0
|
0
|
F16=x2^
|
Инверсия х2- НЕ х2
|
1
|
0
|
1
|
0
|
4. Контрольные вопросы.
Назначение и основы работы с генератором слов.
Назначение и основы работы с логическим анализатором.
Назначение и использование индикаторов в цифровых схемах.
Сформулируйте основные законы алгебры логики.
Приведите пример разложения функции конституэнты 1.
Приведите пример разложения функции конституэнты 0.
Сформулируйте последовательность действий необходимых для синтеза логической схемы устройства.
|
|
|
 Скачать 2.57 Mb.
Скачать 2.57 Mb.












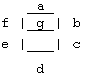

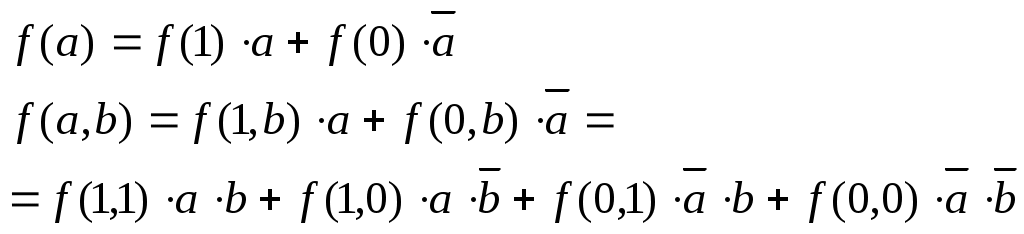 (3.1)
(3.1)