Комплексные числа
 Скачать 191 Kb. Скачать 191 Kb.
|
|
Тема: Комплексные числа 1. Мнимая единица Число, квадрат которого равен -1, называется мнимой единицей 2. Алгебраическая запись комплексного числа z = a + bi. Число a - действительная часть числа z, число bi– мнимая часть числа z. Также комплексные числа можно записывать, например, в виде z=x+yi z=u+vi 3. Изображение комплексных чисел 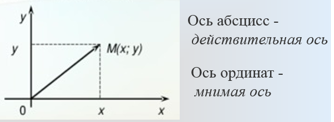 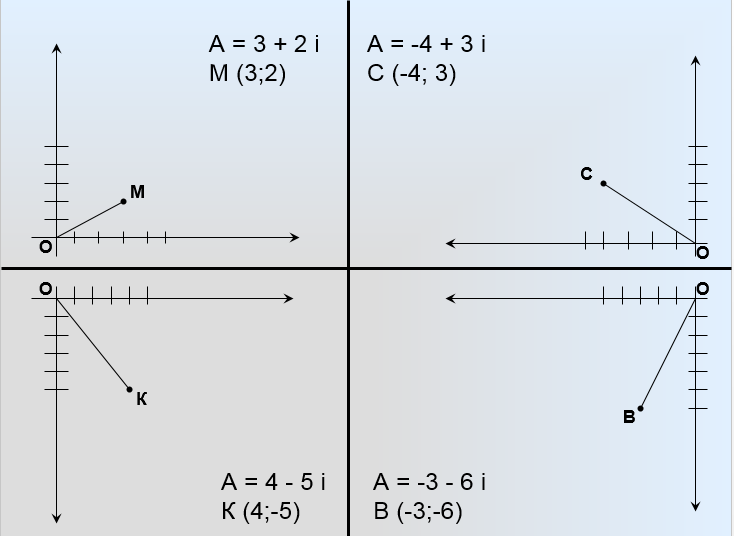 4. Действия с комплексными числами в алгебраической форме 5. Тригонометрическая форма комплексного числа  6. Модуль и аргумент комплексного числа Модулем комплексного числа называется неотрицательное действительное число. (2). Геометрически модуль комплексного числа — это длина вектора, изображающего число z, или полярный радиус точки (x, y). Аргумент комплексного числа z — это угол между положительным направлением действительной оси и вектором z (геометрически – это полярный угол точки (x, y)).  7. Перевод из алгебраической формы в тригонометрическую и наоборот При переходе от алгебраической формы комплексного числа к тригонометрической достаточно определить главное значение аргумента комплексного числа z, то есть считать φ=arg z. Знаки полученных значений cos φ и sin φ по формулам (7.5), дают возможность определить, какой координатной четверти принадлежит угол φ. 8. Действия с комплексными числами в тригонометрической форме: умножение и деление Умножение Произведением комплексных чисел: 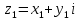 и и 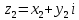 называется комплексное число, определяемое равенством 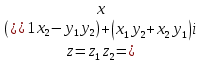 Деление определяется как действие, обратное умножению. Частным двух комплексных чисел 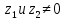 называется комплексное число z, которое будучи умноженным на называется комплексное число z, которое будучи умноженным на 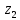 , дает число , дает число 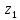 , т.е. , т.е. 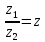 , если , если 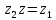 . .Если 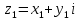 , , 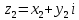 , , 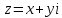 , то , то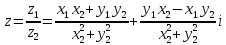 9. Действия с комплексными числами в тригонометрической форме: возведение в степень и извлечение корня Если комплексное число задано в тригонометрической форме, то для возведения его в степень используется формула Муавра: т. е. при возведении комплексного числа в степень модуль возводится в эту степень, а аргумент умножается на показатель степени. Тема: Пределы и непрерывность 1. Вычисление предела функции в точке 2. Правила вычисления предела на бесконечности 3. Замечательные пределы 4. Правило Лопиталя 5. Определение непрерывной функции 6. Классификация точек разрыва 7. Асимтоты к графику функции: опредение, виды 8. Поиск наклонных асимтот к графику функции |
