совершенные числа. Конкурс творческих и исследовательских работ младщих школьников Страна чудес страна исследований
 Скачать 458.5 Kb. Скачать 458.5 Kb.
|
ВВЕДЕНИЕ Цель: исследование совершенных чисел. Задачи: Выяснить, что такое совершенные числа; Научиться находить совершенные числа; Познакомиться с историей открытия совершенных чисел; Изучить свойства совершенных чисел. Актуальность: До сих пор люди ищут и не могут пока найти ответы на многие вопросы, связанные с совершенными числами. И в наши дни люди ищут эти числа. Гипотеза: совершенные числа — одна из интересных и до конца не изученных страниц истории математики. Мой любимый школьный предмет – математика. Мне интересно решать задачи, я с большим удовольствием участвую в различных олимпиадах по этому предмету. Но когда мы изучали тему «наибольший общий делитель», мне показалось, что это скучноватое и однообразное занятие - работать все время по одному и тому же алглритму. Но когда я сказала об этом нашему учителю матаматики, она ответила, что делители - это одно из самых интересных и даже загадочных понятий в математике, нужно лишь почитать кое-что за границами учебника. Я решила последовать ее совету и очень скоро убедилась в том, что это действительно так. Я узнала очень много нового и интересного, открыла для себя загадочный мир совершенных чисел, решила много интересных задач. И эта тема перестала быть для меня скучной, так как за сухими цифрами и числами я увидела гармонию, красоту и совершенство. Так родилась моя исследовательская работа. ГЛАВА I. ЧТО ТАКОЕ СОВЕРШЕННЫЕ ЧИСЛА С древних времен люди, изучая натуральные числа, придавали некоторым из них особые, порой магические свойства. Кроме этого, античные математики считали важным вместе с каждым числом рассматривать все его делители, отличные от самого этого числа. Такие делители называют собственными. При этом если сумма всех собственных делителей оказывалась меньше числа, его назвали недостаточным, а если больше, то избыточным. Так, для числа 10 сумма делителей 1 + 2 + 5 = 8 < 10, поэтому 10 – число «недостаточное», для числа 12 1 + 2 + 3 + 4 + 6 = 16 > 12, значит, 12 – «избыточное» число. А у числа 6 сумма собственных делителей равна самому числу: 1 + 2 + 3 = 6. Такие числа древние ученые особенно ценили и назвали их совершенными. ГЛАВА II. ПОИСК СОВЕРШЕННЫХ ЧИСЕЛ В поиске совершенных чисел я сначала решила пойти по пути античных математиков и проверила первые 100 натуральных чисел. Вот что у меня получилось (рис.1): Р 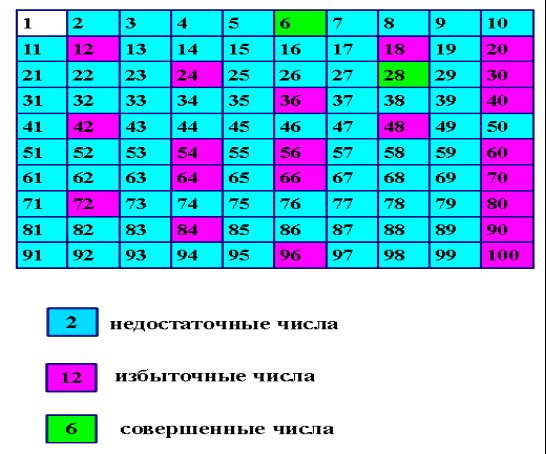 ис.1 Из таблицы видно: 1.Больше всего среди них недостаточных чисел. 2.Среди первых 100 чисел совершенными оказались только числа 6 и 28. Очень долгое время были известны только эти два числа, и никто не знал, существуют ли еще совершенные числа и сколько их вообще может быть. И только спустя несколько столетий Евклид доказал, что всякое число, которое может быть представлено в виде выражения 2 p–1 * (2 p – 1), где (2 p – 1) – простое число, является совершенным числом, – эта теорема теперь носит его имя. Попробуем, воспользовавшись этой формулой, повторить путь первооткрывателей совершенных чисел (табл 1). Таблица.1
ГЛАВА III. ИСТОРИЯ ОТКРЫТИЯ СОВЕРШЕННЫХ ЧИСЕЛ Таким образом, я нашла еще 3 совершенных числа. Но я пользовалась калькулятором, поэтому сделала это достаточно быстро. А вот математикам древности было гораздо сложнее - достаточно сказать, что пятое совершенное число 33550336 (р = 13) было найдено спустя более тысячи лет после четвертого! Да и в последующие пять веков совершенные числа собирались буквально «по крупицам». Нахождение каждого из них было событием в мире математики. В чем же дело? Проблема оказалась в числах 2p– 1 (их называют числами Мерсенна). Вычислить любое из них совсем нетрудно, но выяснить, является ли оно простым – это выходило далеко за пределы человеческих сил. Так, в 1932 году американский математик Деррик Генри Лемер (1905–1991) занимался поисками тринадцатого свершенного числа для p= 257. Ему пришлось работать целый год, пользуясь известными тогда счетными приборами, чтобы выяснить, является ли простым число 2257– 1, но в результате он убедился, что это число составное, и двенадцатое совершенное число оставалось наибольшим до 1952 года.С этого времени, когда людям на помощь пришла счетная электронная машина и более современные компьютерные технологии, поиск совершенных чисел пошел гораздо быстрее. Но даже на сегодняшний день известно всего лишь 49 простых чисел Мерсенна и соответствующих им совершенных чисел Самым большим известным совершенных числом является число 274207281 – 1 {\displaystyle M_{74207281}=2^{74207281}-1} , найденное 7 января 2016 года Кертисом Купером (англ). Оно с {\displaystyle M_{74207281}} одержит 22 338 618 цифр. Вот что я узнала об истории открытия некоторых из них (табл. 2): Таблица. 2
ГЛАВА IV. СВОЙСТВА СОВЕРШЕННЫХ ЧИСЕЛ Никомах Герасский (I–II век н.э.), знаменитый греческий философ и математик, писал: Совершенные числа красивы. Красивые вещи редки и немногочисленны... Избыточными и недостаточными бывают все числа, в то время как совершенных чисел немного. В чем же их красота? Может быть, в том, что они обладают рядом таинственных и вместе с тем замечательных свойств. Некоторые из них я проверила: 1. Все совершенные числа, кроме 6, являются суммой кубов последовательных нечётных натуральных чисел: 28 = 13 + 33; 496 = 13 + 33 + 53 + 73; 8 128 = 13 + 33 + 53 + 73 + 93 + 113 + 133 + 153. 2. Все совершенные числа являются треугольными (рис 2,3). 6 = 1 + 2 + 3; 28 = 1 + 2 + 3 + 4 + 5 + 6 + 7; 4   96 = 1 + 2 + 3 + …. + 30 + 31 Рис.2 Рис.3 3. Сумма всех чисел, обратных делителям совершенного числа, равна 2. 4. Сумма всех цифр совершенного числа, кроме 6, равна 1: 28. 2 + 8 = 10, 1 + 0 = 1; 496. 4 + 9 + 6 = 19, 1 + 9 = 10, 1 + 0 = 1; 8128 8 + 1 + 2 + 8 = 19, 1 + 9 = 10, 1 + 0 = 1; 33550336 3 + 3 + 5 + 5 + 0 + 3 + 3 + 6 = 28, 2 + 8 = 10, 1 + 0 = 1 ЗАКЛЮЧЕННИЕ Вот почти и все, что за 2 тысячелетия люди узнали об этих, на первый взгляд, обычных, но как оказалось действительно удивительных числах. Но даже столь немногое вызывает уважение. Не зря им дано такое название — они его полностью оправдывают. В выполнения данной работы я: узнала, какие числа называются совершенными; выяснила, какими свойствами обладают совершенные числа и проверила некоторые из них; нашла 5 первых совершенных чисел; познакомилась с историей открытия совершенных чисел. Я убедилась в своем предположении. Совершенные числа — действительно одна из интересных и до конца не изученных страниц истории математики. До сегодняшнего дня остаются без ответа два важных вопроса: существует ли нечетное совершенное число и существует ли наибольшее четное совершенное число? До сих пор не найдено ни одного нечетного совершенного числа, но вместе с тем и не доказано, что такого числа не существует. И до сих пор люди занимаются поиском простых чисел Мерсенна и соответствующих им совершенных чисел. В Интернете в 1996 году запущен специальный проект распределённых вычислений GIMPS по поиску простых чисел Мерсенна, в котором может принять участие любой желающий. Список литературы 1.http://math4school.ru/sovershennie_chisla.html 2.https://ru.wikipedia.org/wiki/%D0%A1%D0%BE%D0%B2%D0%B5%D1%80%D1%88%D0%B5%D0%BD%D0%BD%D0%BE%D0%B5_%D1%87%D0%B8%D1%81%D0%BB%D0%BE 3.http://www.arbuz.uz/z_sov1.html 4.http://kvant.mccme.ru/1991/05/sovershennye_chisla.htm | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
