2_Учебное пособие. 2_Учебное пособие doc. Конспект лекций для 1 семестра изучения курса Физика I. Механика и элементы специальной теории относительности 1

• Название: Конспект лекций для 1 семестра изучения курса Физика I. Механика и элементы специальной теории относительности 1
• Анкор: 2_Учебное пособие
• Дата: 02.06.2022
• Размер: 3.78 Mb.
• Имя файла: 2_Учебное пособие doc.doc
• Тип: Конспект лекций; #564609
• страница: 2 из 4

Законы Ньютона

Первый закон Ньютона: всякое тело находится в состоянии покоя или равномерного прямолинейного движения, пока воздействие со стороны других тел не выведет его из этого состояния.

Тела, не подверженные внешним воздействиям, называются свободными телами. Система отсчёта, связанная со свободным телом, называется инерциальной системой отсчёта (ИСО). По отношению к ней любое свободное тело будет двигаться равномерно и прямолинейно или находиться в состоянии покоя. Из относительности движения следует, что система отсчёта, движущаяся равномерно и прямолинейно по отношению к ИСО, также является ИСО. ИСО играют важную роль во всех разделах физики. Это связано с принципом относительности Эйнштейна, согласно которому математическая форма любого физического закона должна иметь один и тот же вид во всех инерциальных системах отсчёта.

К основным понятиям, используемым в динамике поступательного движения, относятся сила, масса тела, импульс тела (системы тел).

Силой называется векторная физическая величина, являющаяся мерой механического действия одного тела на другое. Механическое действие возникает как при непосредственном контакте взаимодействующих тел (трение, реакция опоры, вес и т.д.), так и посредством силового поля, существующего в пространстве (сила тяжести, кулоновские силы и т.д.). Сила характеризуется модулем, направлением и точкой приложения.

Одновременное действие на тело нескольких сил , ,..., может быть заменено действием результирующей (равнодействующей) силы :

= + +...+ = .

Массой тела называется скалярная величина, являющаяся мерой инертности тела. Под инертностью понимается свойство материальных тел сохранять свою скорость неизменной в отсутствие внешних воздействий и изменять её постепенно (т.е. с конечным ускорением) под действием силы.

Импульсом тела (материальной точки) называется векторная физическая величина, равная произведению массы тела на его скорость: .

Импульс системы материальных точек равен векторной сумме импульсов точек, составляющих систему: .

Второй закон Ньютона: скорость изменения импульса тела равна действующей на него силе:

.
Если масса тела остается постоянной, то ускорение, приобретаемое телом относительно инер­ци­аль­ной системы отсчета, прямо пропорционально действующей на него силе и обратно пропорционально массе тела:

.

Третий закон Ньютона: силы, с которыми действуют друг на друга взаимо­дей­ствующие тела, равны по величине и противоположны по направлению:

,

где – сила, действующая на первое тело со стороны второго,

– сила, действующая на второе тело со стороны первого.

Из третьего закона следует, что в любой механической системе материальных то­чек геометрическая сумма всех внутренних сил (т.е. сил, с которыми взаимо­действуют между собой материальные точки системы) равна нулю.
2.2. Динамика вращательного движения твердого тела
Вращательное действие силы харак­те­ризуется мо­ментом силы относительно точки (рис. 5а) и относительно оси (рис. 5б).

Для того чтобы определить момент силы относительно точки О, проведем из точки О радиус-вектор в точку приложения силы (рис. 5а). Моментом силы относительно точки О называется векторная физическая величина, равная векторному произведению радиуса-вектора на силу :



Модуль момента силы M = rFsin = Fd, где d = rsin – плечо силы.

Для того чтобы определить момент силы относительно оси Z, выберем на оси Z произвольную точку, найдем момент силы относительно этой точки, а затем спроецируем на ось Z момент силы относительно точки. Таким образом, момент силы относительно оси – величина скалярная.

Разложим силу на три составляющие (рис. 5б):

– осевая, параллельная оси вращения,

– радиальная, перпендикулярная оси вращения,

– касательная, перпендикулярная и оси вращения.

Составляющую можно определить как проекцию силы на направление вектора , направленного по касательной к окружности радиусом R, проведенной через точку приложения силы перпендикулярно оси вращения. Направление вектора образует с осью Z правовинтовую систему.

Составляющие 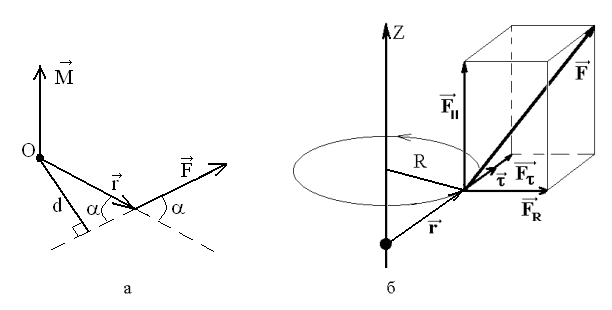и вращения тела относительно оси Z не вызывают. Вращающее действие силы обусловлено составляющей . Можно показать, что момент силы относительно оси Z





Рис. 5
Инертные свойства тела при вращательном движении характеризует момент инерции. Он зависит от распределения массы тела относительно оси вращения. Момент инерции материальной точки массой m, находящейся на расстоянии r от оси: .

– момент инерции системы материальных точек;

– момент инерции тела, где – плотность тела.

Рис. 6

Момент инерции тела относительно произвольной оси может быть рассчитан по теореме Штейнера: момент инерции тела относительно оси O'O равен сумме момента инерции тела относительно оси, проходящей через центр инерции и параллельной O'O, и произведения массы тела на квадрат расстояния между осями (рис. 6): .

Моментом импульса материальной точки относительно некоторой точки называется векторная величина, равная векторному произведению радиуса-вектора на импульс материальной точки (рис. 7а):

.

Моментом импульса системы материальных точек называется геометрическая сумма моментов импульсов точек, составляющих систему:

.

Моментом импульса материальной точки относительно оси Z называется скалярная величина, равная проекции момента импульса относительно произвольной точки, лежащей на оси Z, на эту ось. Аналогично моменту силы относительно оси, момент импульса относительно оси Z



где p_ – проекция импульса на направление вектора 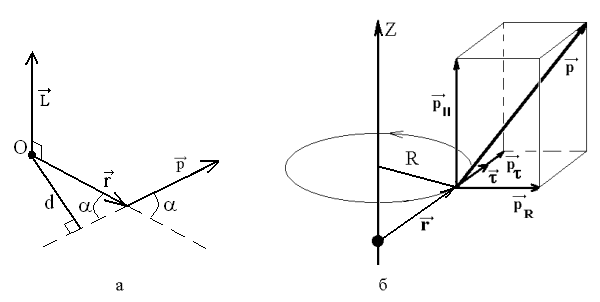, направленного по касательной к окружности радиусом, проведенной через материальную точку перпендикулярно оси вращения (рис. 7б). Направление вектора образует с осью Z правовинтовую систему.



Рис. 7
Момент импульса тела относительно оси вращения

L_Z = I_Z_Z,

где I_Z – момент инерции тела относительно оси Z, _Z – проекция угловой скорости тела на ось Z. Для однородного тела, вращающегося относительно оси симметрии:

.
Основной закон динамики вращательного движения:

Скорость изменения момента импульса тела относительно оси равна результирующему моменту внеш­них сил относительно этой же оси (проекция углового ускорения на ось пропор­циональна результирующему моменту внешних сил относительно оси и обратно пропорциональна моменту инерции тела относительно этой же оси):



Из законов динамики поступательного и вращательного движений следует условие равновесия тел:


3. Работа и механическая энергия

3.1. Работа и мощность при поступательном и вращательном движениях
Работа – это физическая величина, характеризующая процесс превращения одной формы движения в другую. В механике принято говорить, что работа совершается силой.

Элементарной работой силы называется величина, равная скалярному произведению силы на элементарное перемещение :

,

где – элементарный путь точки приложения силы за время dt,  – угол между векторами и .

Если на систему действуют несколько сил, то результирующая работа равна алгебраической сумме работ, совершаемых каждой силой в отдельности. Работа силы на конечном участке траектории или за конечный промежуток времени может быть вычислена следующим образом:

.

Если = const, то А=  .

При вращательном движении работа определяется проекцией момента сил на направление угловой скорости: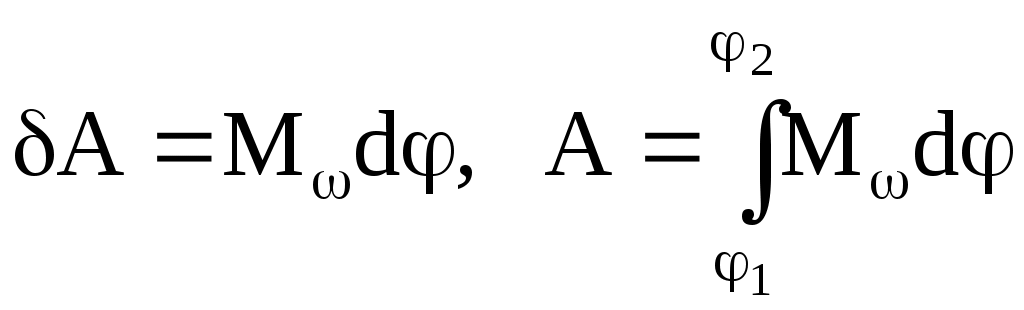

,

если М_ = const, то А = М_.

Быстроту совершения работы характеризует мощность. Мощностью называется скалярная величина, равная работе, совершаемой в единицу времени:

– средняя мощность; – мгновенная мощность.

При вращательном движении мощность определяется следующим образом:

.

3.2. Консервативные и неконсервативные силы
Консервативными силами называются силы, работа которых не зависит от пути перехода тела или системы из начального положения в конечное. Характерное свойство таких сил – работа на замкнутой траектории равна нулю:



К консервативным силам относятся: сила тяжести, гравитационная сила, сила упругости и другие силы.

Неконсервативными силами называются силы, работа которых зависит от пути перехода тела или системы из начального положения в конечное. Работа этих сил на замкнутой траектории отлична от нуля. К неконсервативным силам относятся: сила трения, сила тяги и другие силы.
3.3. Кинетическая энергия при поступательном и вращательном движениях
Кинетической энергией тела называется функция механического состояния, зависящая от массы тела и скорости его движения (энергия механического движения).

Кинетическая энергия поступательного движения . Кинетическая энергия вращательного движения .

При сложном движении твёрдого тела его кинетическая энергия может быть представлена через энергию поступательного и вращательного движения:

.
Свойства кинетической энергии.

1. Кинетическая энергия является конечной, однозначной, непрерывной функ­цией механического состояния системы.

2. Кинетическая энергия не отрицательна: Е_К 0.

3. Кинетическая энергия системы тел равна сумме кинетических энергий тел, составляющих систему.

4. Приращение кинетической энергии тела равно работе всех сил, действу­ю­щих на тело: .
3.4. Потенциальная энергия
Потенциальная энергия системы – это функция механического состояния системы, зависящая от взаимного расположения всех тел системы и от их положения во внешнем потенциальном поле сил. Убыль потенциальной энергии равна работе, которую совершают все консервативные силы (внутренние и внешние) при переходе системы из начального положения в конечное.

Е_П1 - Е_П2 = Е_П = А_12конс, .

Из определения потенциальной энергии следует, что она может быть определена по консервативной силе, причём с точностью до произвольной постоянной, значение которой определяется выбором нулевого уровня потенциальной энергии.

.

Таким образом, потенциальная энергия системы в данном состоянии равна работе, совершаемой консервативной силой при переводе системы из данного состояния на нулевой уровень.

Свойства потенциальной энергии.

1. Потенциальная энергия является конечной, однозначной, непрерывной

функ­цией механического состояния системы.

2. Численное значение потенциальной энергии зависит от выбора уровня с

нулевой потенциальной энергией.

Как потенциальная энергия может быть найдена по известной консервативной силе, так и консервативная сила может быть найдена по потенциальной энергии:

,

причем , , .

Примеры потенциальной энергии:

1) – потенциальная энергия тела массой m, поднятого на высоту h относительно нулевого уровня энергии в поле силы тяжести;

2. 
   – потенциальная энергия упругого деформированного тела, х – деформация тела.
   

4. Законы сохранения в механике

4.1. Закон сохранения механической энергии
Механическая энергия системы тел равна сумме их кинетических энергий и потенциальной энергии взаимодействия этих тел друг с другом и с внешними телами:

Е = Е_к + Е_п.

Приращение механической энергии системы определяется работой всех неконсервативных сил (внешних и внутренних):

.

Закон сохранения механической энергии: механическая энергия системы тел, на которые действуют только консервативные силы, остается постоянной.
4.2. Закон сохранения импульса. Центральный удар двух тел
Закон сохранения импульса: полный импульс замкнутой системы остается посто­янным.

Для замкнутой системы будут сохраняться и проекции импульса на координатные оси:

.

Если 0, но =0, то будет сохраняться проекция импульса системы на ось Х.

Рассмотрим центральный удар двух тел. Центральным называется удар, при котором тела движутся вдоль прямой, соединяющей их центры масс. Выделяют два предельных вида такого удара: абсолютно упругий и абсолютно неупругий.

Для двух тел массами m₁ и m₂ , движущихся со скоростями и вдоль оси х, проекции их скоростей на ось х после абсолютно упругого центрального удара можно найти по формулам:
; .

При этом сохраняются импульс и механическая энергия системы тел.
Если удар абсолютно неупругий, то

.

Тела после такого удара движутся вместе. Импульс системы тел сохраняется, а полная механическая энергия не сохраняется. Часть механической энергии переходит в энергию неупругой деформации и во внутреннюю энергию тел.

4.3. Закон сохранения момента импульса
Закон сохранения момента импульса: момент импульса замкнутой системы тел сохраняется:

если .

Если результирующий момент внешних сил не равен нулю, но равна нулю его проекция на некоторую ось, то проекция момента импульса системы на эту ось не изменяется.


5. Элементы специальной теории относительности

5.1. Постулаты Эйнштейна. Преобразования Лоренца