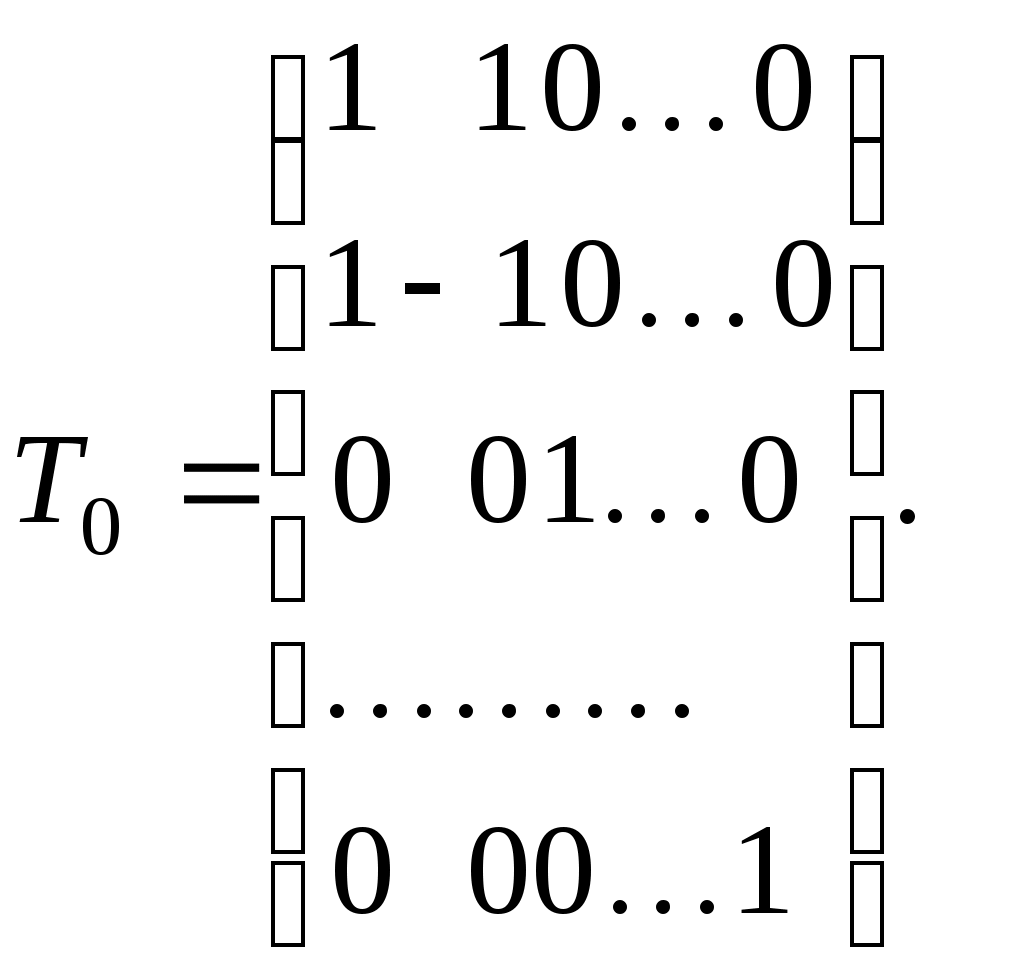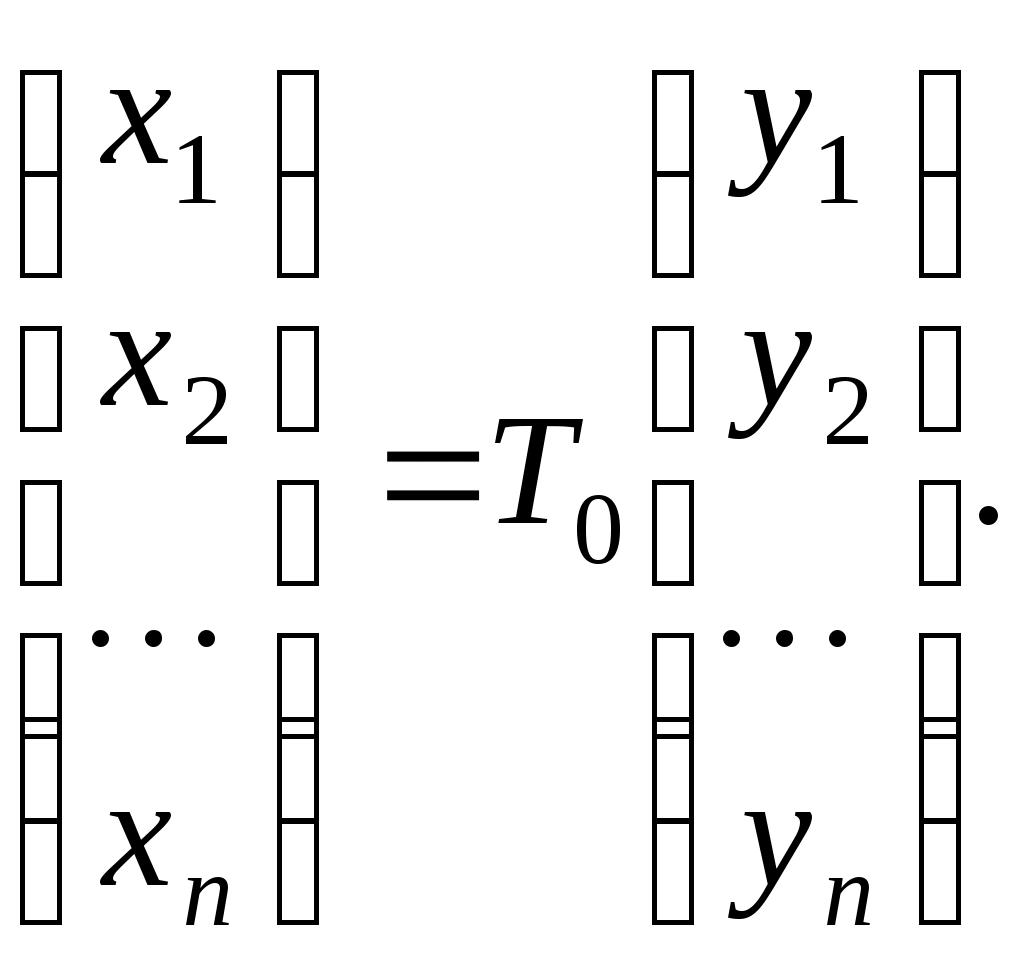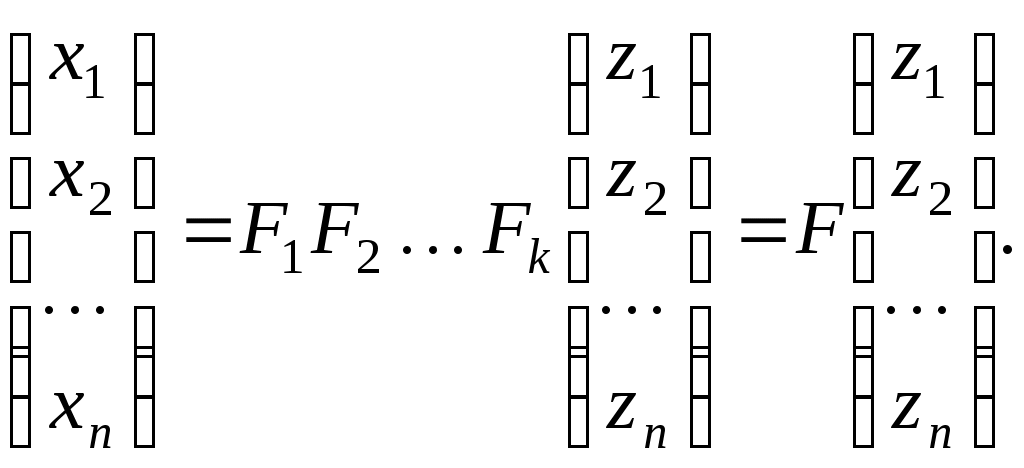|
|
Билинейные формы Шестаков. Білінійні та квадратичні функції С. С. Шестаков. Конспект лекцій для студентів заочного відділенння
Квадратичні функції та квадратичні форми
Нехай  - симетрична білінійна функція на векторному просторі - симетрична білінійна функція на векторному просторі  над полем над полем  . .
Означення. Квадратичною функцією  називається функція одного аргументу, яка утворена ототожненням аргументів симетричної білінійної функції називається функція одного аргументу, яка утворена ототожненням аргументів симетричної білінійної функції  , тобто, , тобто, 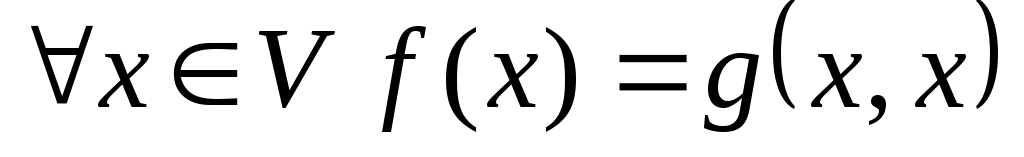 . .
Означення. Симетрична білінійна функція  , яка породжує квадратичну функцію , яка породжує квадратичну функцію  , називається полярною білінійною функцією квадратичної функції , називається полярною білінійною функцією квадратичної функції  . .
Теорема. Для даної квадратичної функції існує єдина полярна білінійна функція.
Доведення. Нехай  - квадратична функція на просторі - квадратична функція на просторі  , ,  - її полярна симетрична білінійна функція. Тоді для даних фіксованих - її полярна симетрична білінійна функція. Тоді для даних фіксованих  , враховуючи симетричність функції , враховуючи симетричність функції  , одержимо: , одержимо:
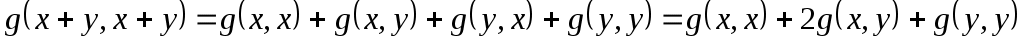 . .
Звідси
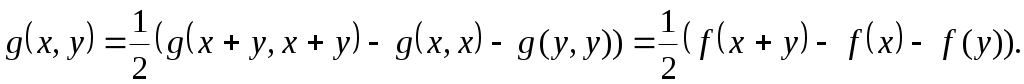
Якщо  - інша полярна білінійна функція, то також виконується - інша полярна білінійна функція, то також виконується
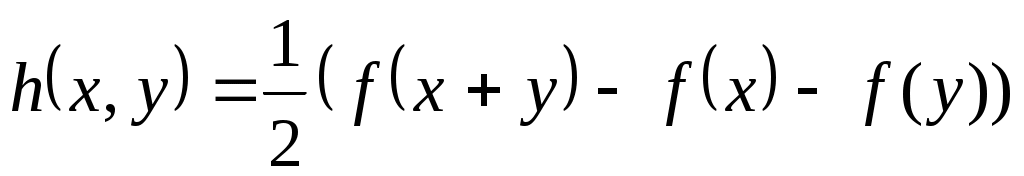 , ,
тобто,
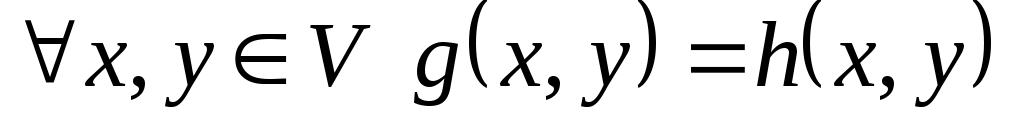 . .
У розумінні цієї теореми дослідження симетричних білінійних функцій зводиться до дослідження квадратичних функцій.
Припустимо, що  - скінченновимірний простір, - скінченновимірний простір,  - деякий фіксований базис простору, - деякий фіксований базис простору,  - довільний вектор, який у цьому базисі задається такими координатами: - довільний вектор, який у цьому базисі задається такими координатами: 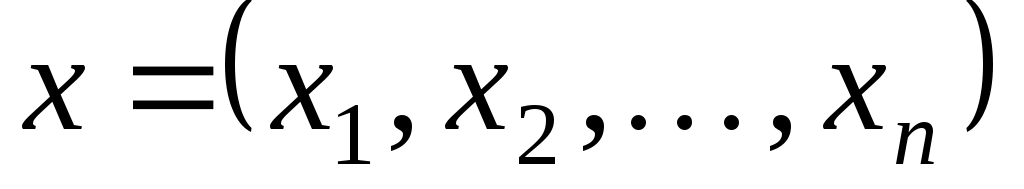 . Тоді . Тоді
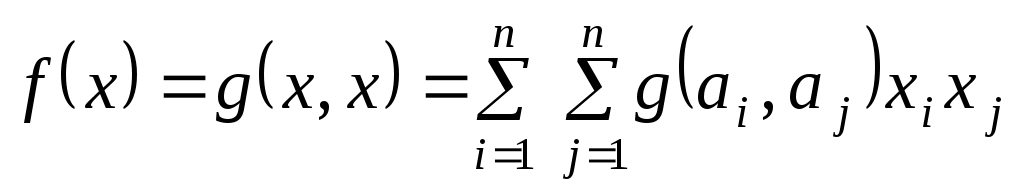 . .
Позначимо
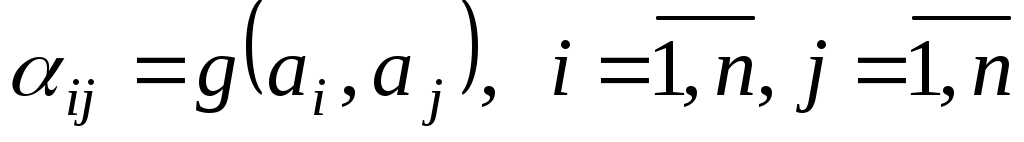 . .
Тоді
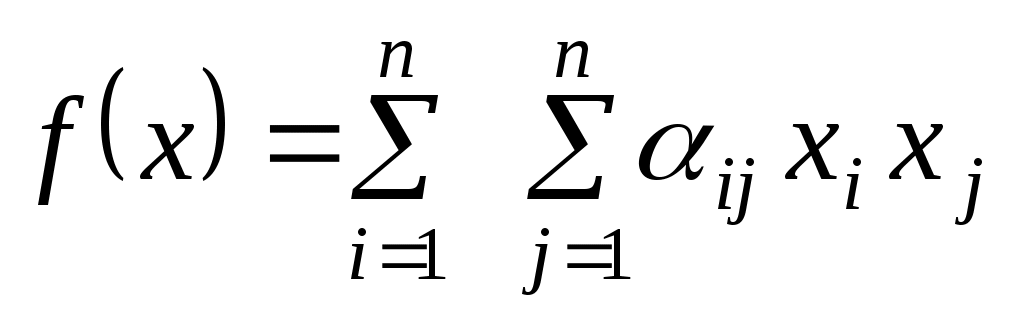 . .
Сума такого вигляду називається квадратичною формою від змінних 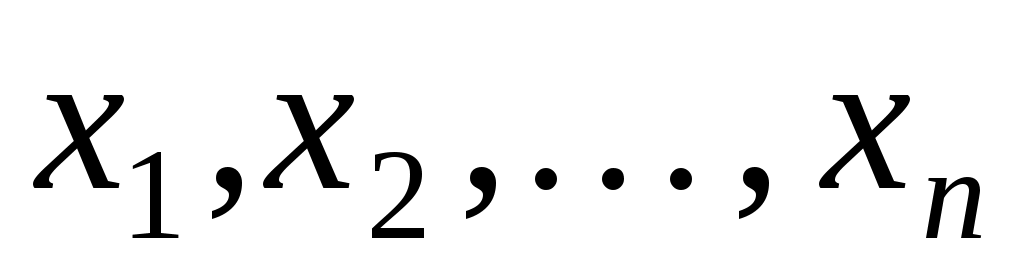 . Таким чином, квадратична функція на скінченновимірному векторному просторі в будь-якому базисі задається деякою квадратичною формою. В цьому розумінні часто ототожнюють поняття квадратичної функції та квадратичної форми. Оскільки в різних базисах квадратична функція задається різними квадратичними формами, то кажуть про вигляд квадратичної форми в тому чи іншому базисі. . Таким чином, квадратична функція на скінченновимірному векторному просторі в будь-якому базисі задається деякою квадратичною формою. В цьому розумінні часто ототожнюють поняття квадратичної функції та квадратичної форми. Оскільки в різних базисах квадратична функція задається різними квадратичними формами, то кажуть про вигляд квадратичної форми в тому чи іншому базисі.
Означення. Матрицею квадратичної функції  у даному базисі у даному базисі  називається матриця в цьому базисі її полярної білінійної функції називається матриця в цьому базисі її полярної білінійної функції  . .
Два способи завдання квадратичних функцій
Припустимо, що  - квадратична функція на скінченновимірному векторному просторі - квадратична функція на скінченновимірному векторному просторі  , ,  - її полярна білінійна функція, - її полярна білінійна функція, 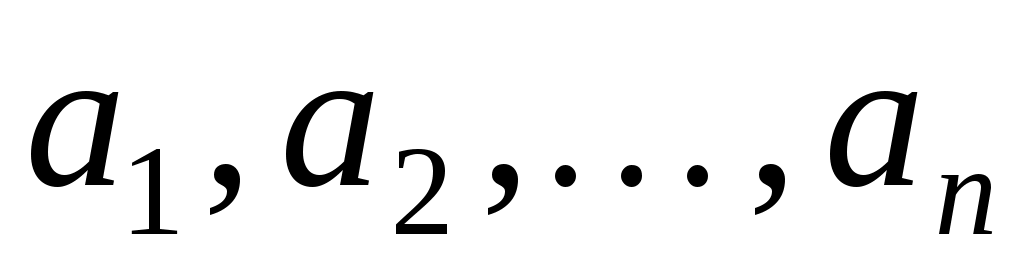 - фіксований базис простору, в якому квадратичній функції відповідає матриця - фіксований базис простору, в якому квадратичній функції відповідає матриця
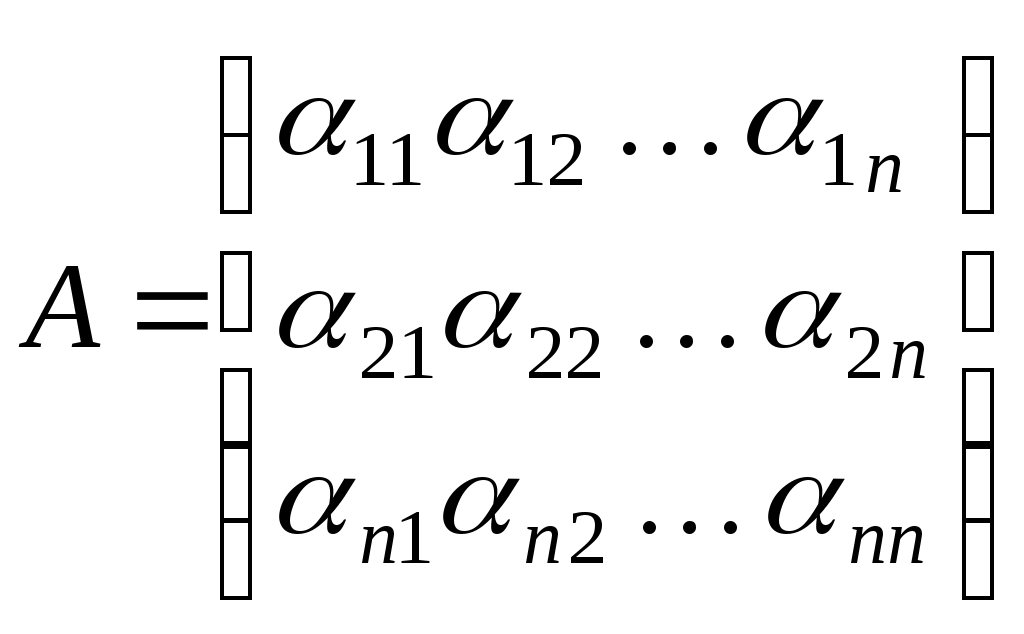 . .
Якщо  - довільний вектор, який у даному базисі має такі координати: - довільний вектор, який у даному базисі має такі координати: 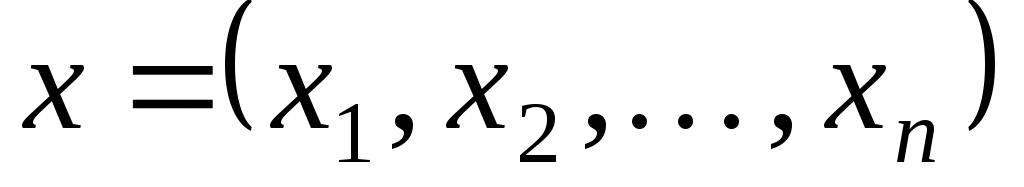 , то , то
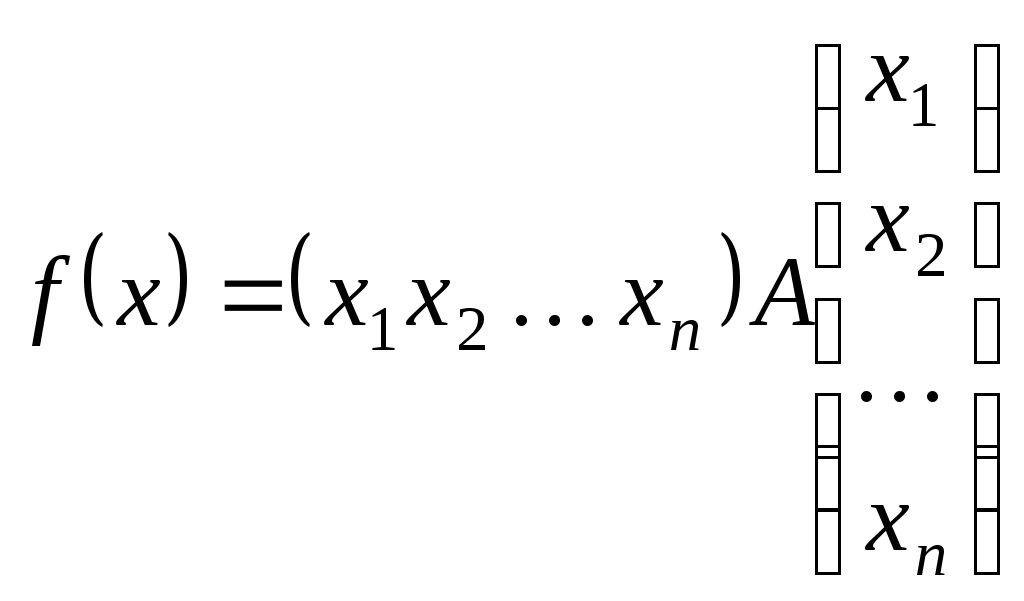 . .
Цей спосіб є матричним способом завдання квадратичної функції.
Перемножимо матриці і отримаємо:
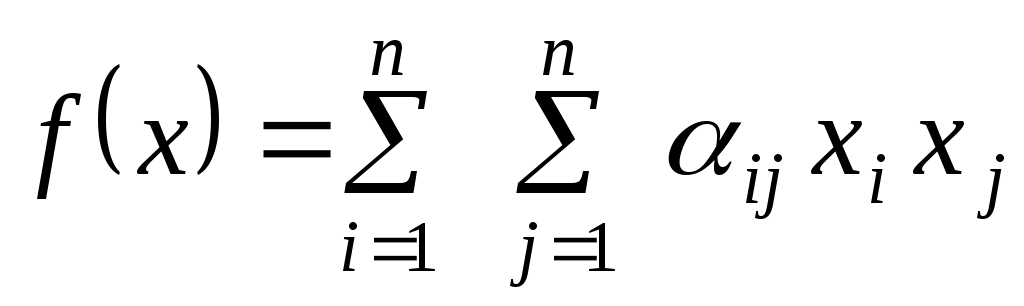 , ,
або, враховуючи симетричність матриці, 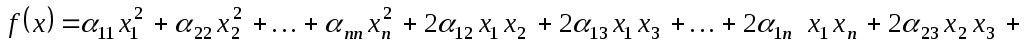
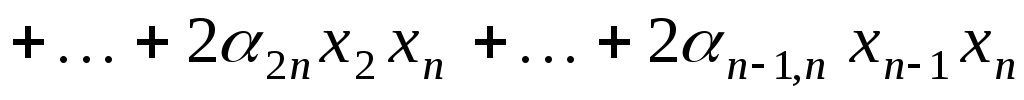 . .
Одержуємо квадратичну форму від  змінних змінних 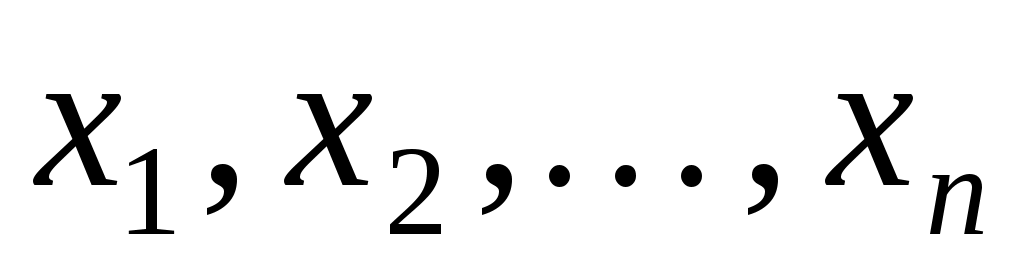 . Цей спосіб є завданням квадратичної функції за допомогою квадратичної форми. . Цей спосіб є завданням квадратичної функції за допомогою квадратичної форми.
Припустимо, що в даному базисі квадратична функція задається квадратичною формою. Виникає питання, як знайти матрицю квадратичної функції в цьому базисі. Неважко бачити, що коефіцієнтами при квадратах змінних є діагональні елементи матриці. Припустимо, що всі члени в квадратичній формі зведені, тоді при 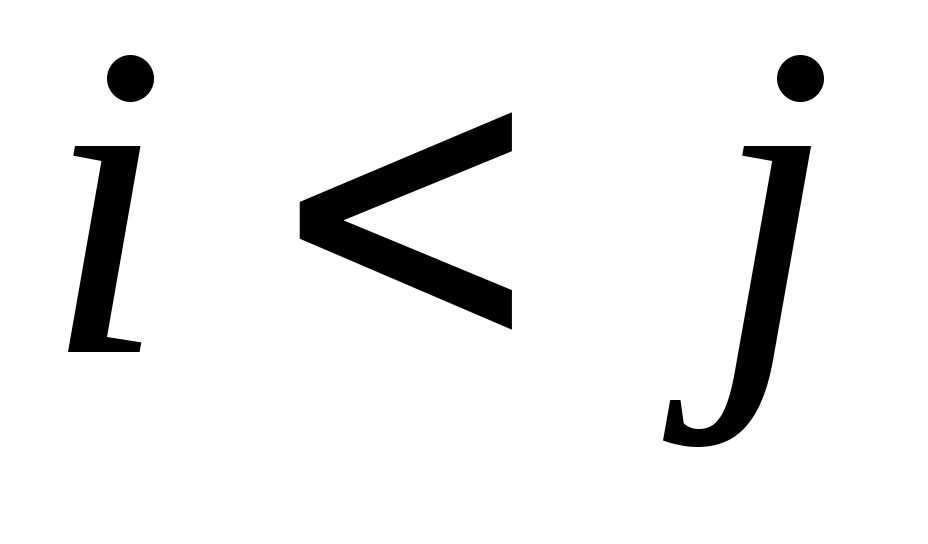 коефіцієнтом при добутку змінних коефіцієнтом при добутку змінних 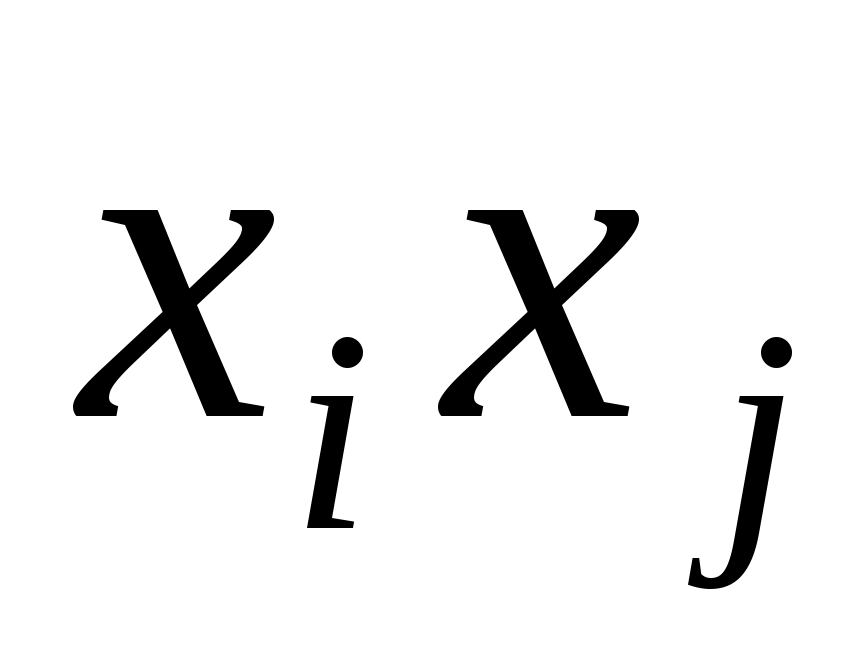 є сума елементів матриці є сума елементів матриці 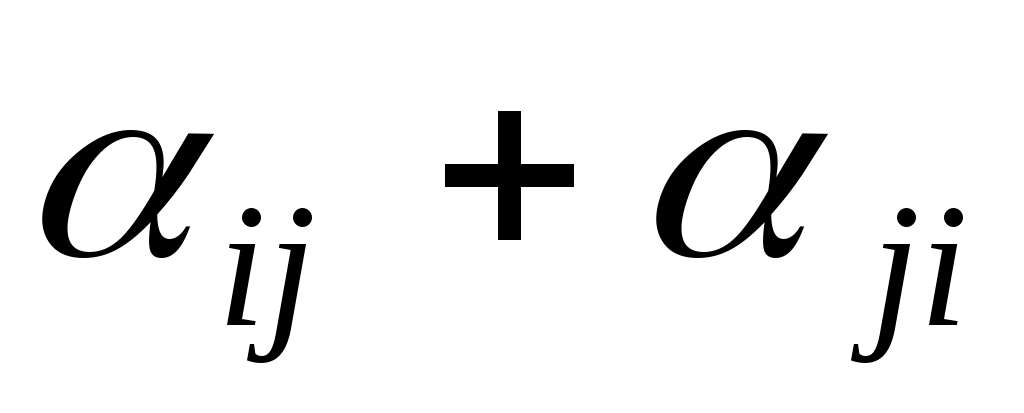 , причому , причому 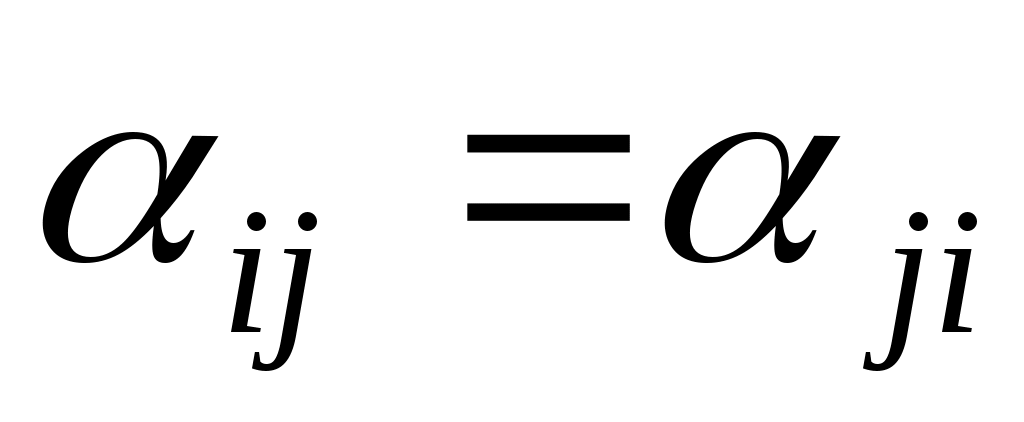 . Звідси випливають наступні правила побудови матриці квадратичної функції. . Звідси випливають наступні правила побудови матриці квадратичної функції.
Визначається, від скількох змінних залежить квадратична форма. Це число дає порядок матриці.
На головній діагоналі матриці виписуються коефіцієнти при квадратах змінних.
Заповнюється верхній трикутник матриці: на місці 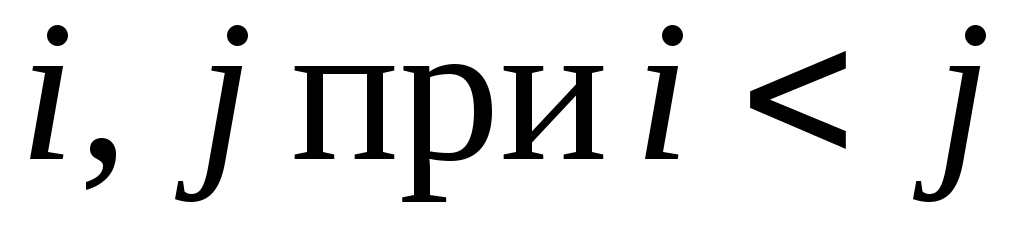 ставиться половина коефіцієнта при добутку змінних ставиться половина коефіцієнта при добутку змінних 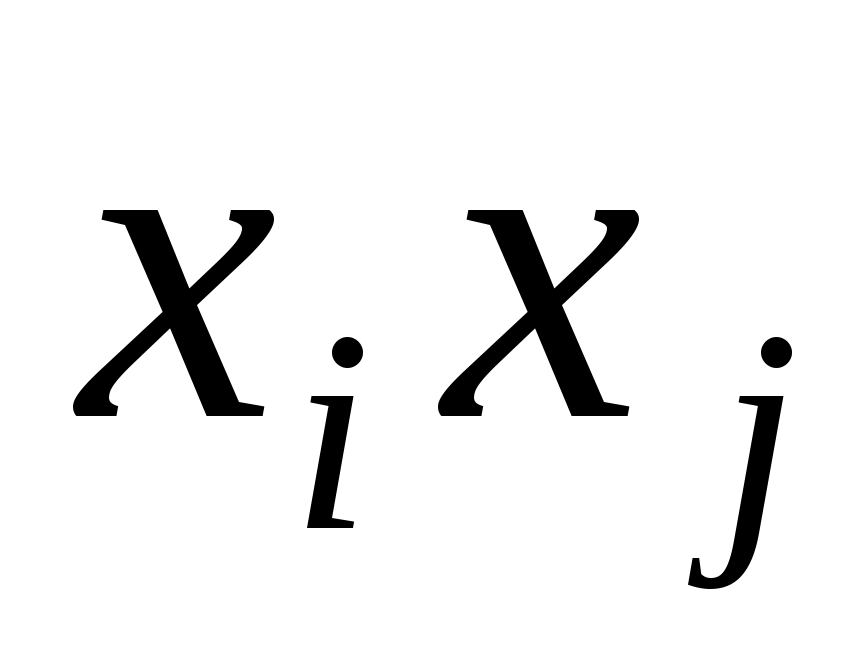 . .
Заповнюється нижній трикутник матриці так, щоби матриця була симетричною.
Зведення квадратичної функції до канонічного вигляду
Нехай 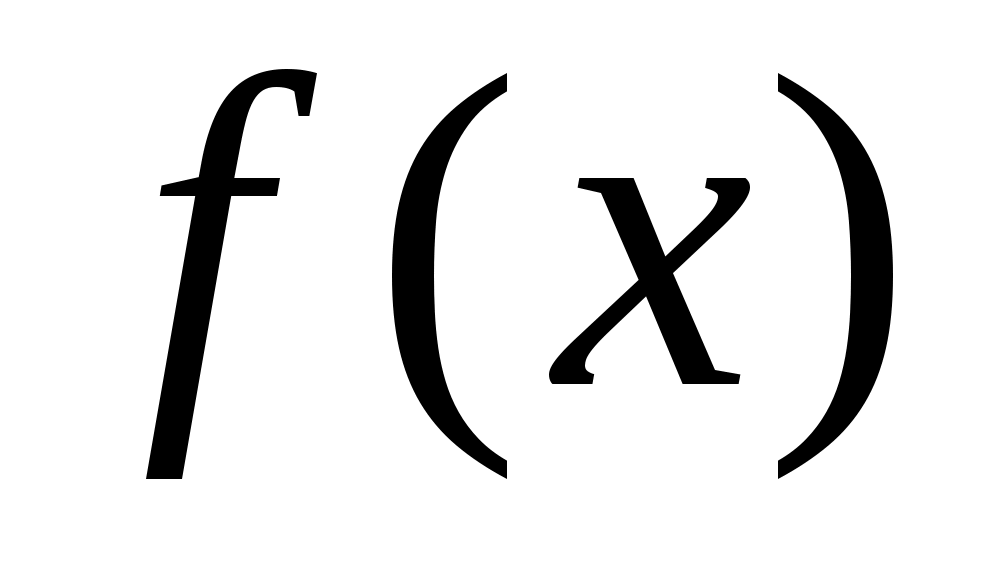 - квадратична функція на скінченновимірному векторному просторі - квадратична функція на скінченновимірному векторному просторі  , , 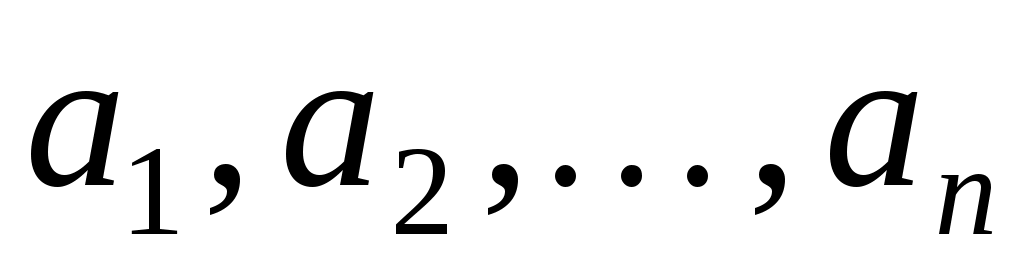 - фіксований базис простору, в якому квадратична функція задається деякою квадратичною формою - фіксований базис простору, в якому квадратична функція задається деякою квадратичною формою
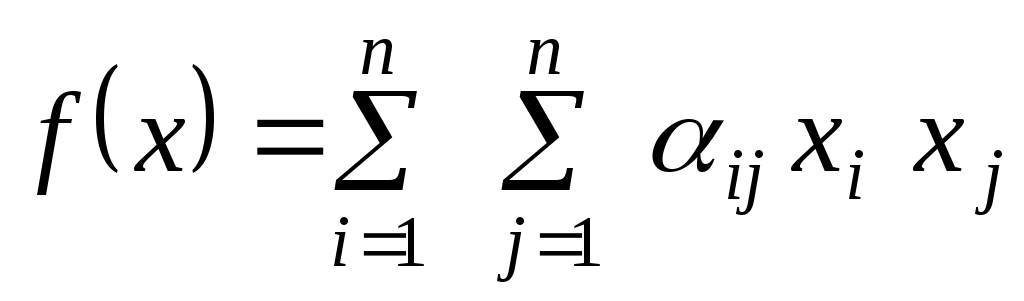 . .
Квадратична форма 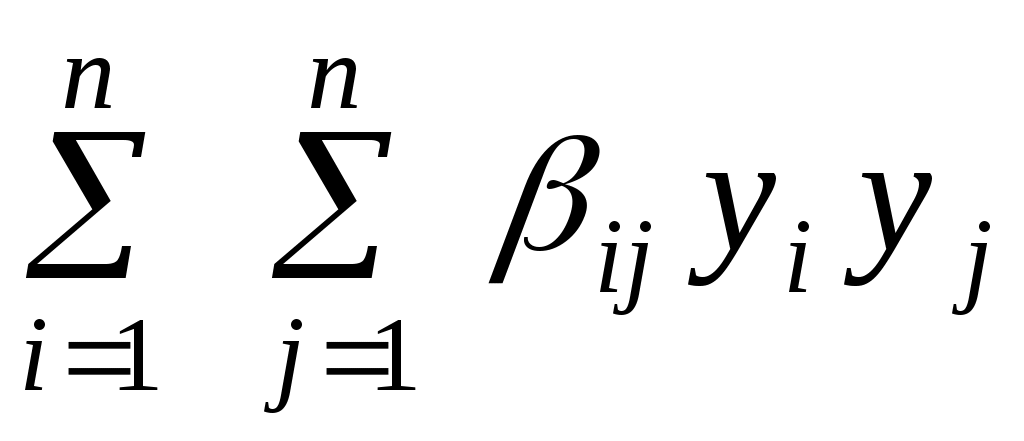 називається канонічною, якщо в ній присутні лише квадрати змінних, тобто, називається канонічною, якщо в ній присутні лише квадрати змінних, тобто,
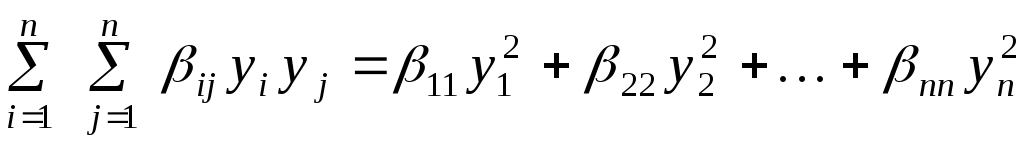  . .
Задача зведення полягає в тому, що, користуючись даним базисом  простору, знаходиться такий базис простору простору, знаходиться такий базис простору 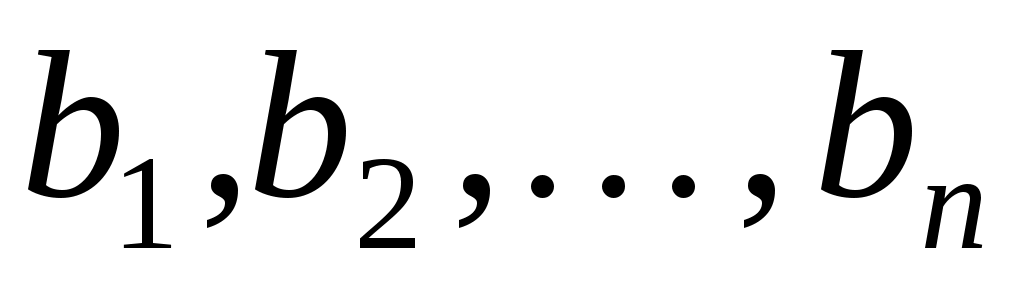 , у якому квадратична функція задається канонічною квадратичною формою. Зрозуміло, що в такому базисі матриця квадратичної функції є діагональною. Звідси - матричне формулювання задачі. Користуючись матрицею , у якому квадратична функція задається канонічною квадратичною формою. Зрозуміло, що в такому базисі матриця квадратичної функції є діагональною. Звідси - матричне формулювання задачі. Користуючись матрицею  квадратичної функції в даному базисі знайти квадратичної функції в даному базисі знайти
невироджену матрицю  , таку, що матриця , таку, що матриця 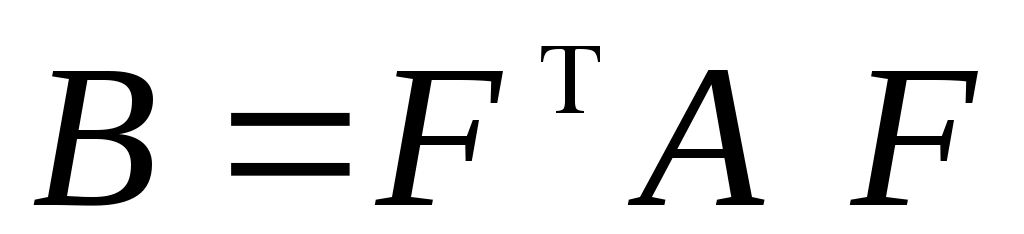 діагональна. Тоді діагональна. Тоді  - матриця переходу до нового базису. - матриця переходу до нового базису.
Згадаємо деякі факти. Нехай 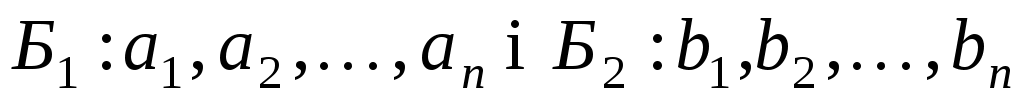 - базиси векторного простору - базиси векторного простору  , ,  - матриця переходу від базису - матриця переходу від базису 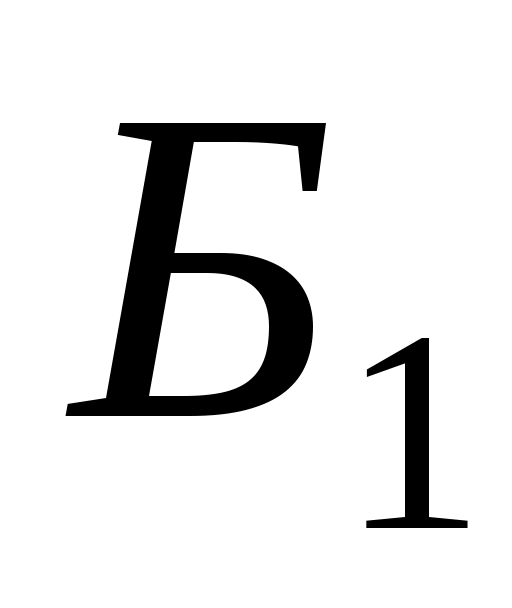 до базису до базису 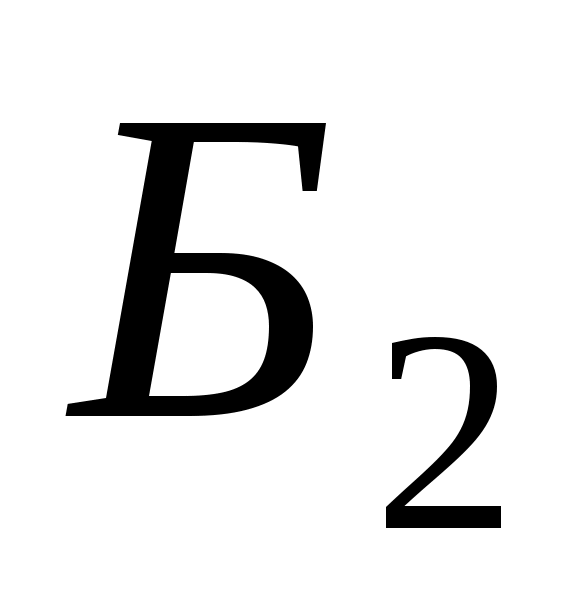 . Якщо довільний вектор . Якщо довільний вектор  у базисі у базисі 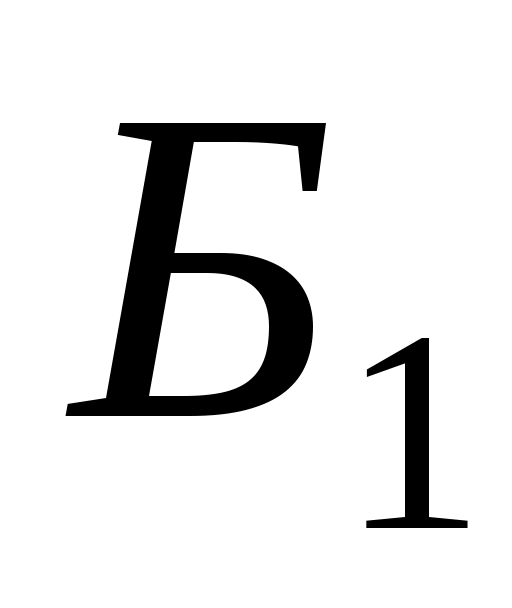 задається координатами задається координатами 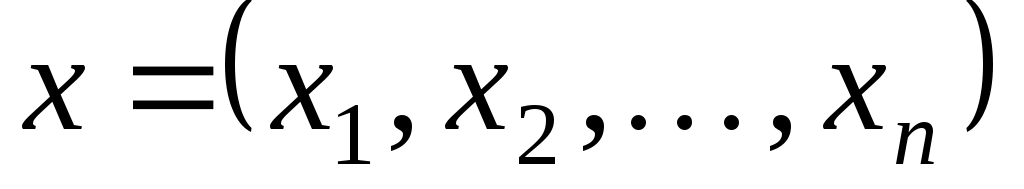 , а в базисі , а в базисі 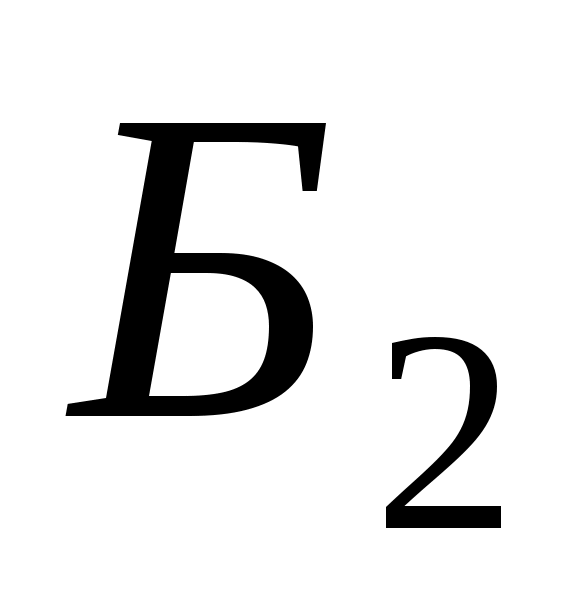 - координатами - координатами 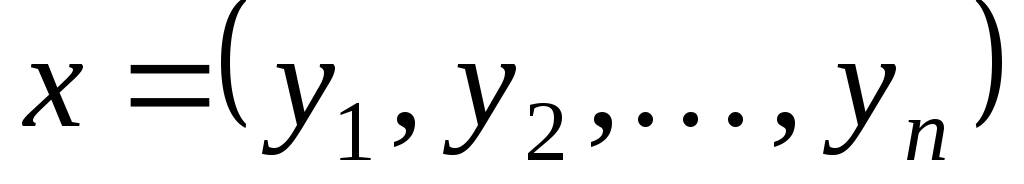 , то , то
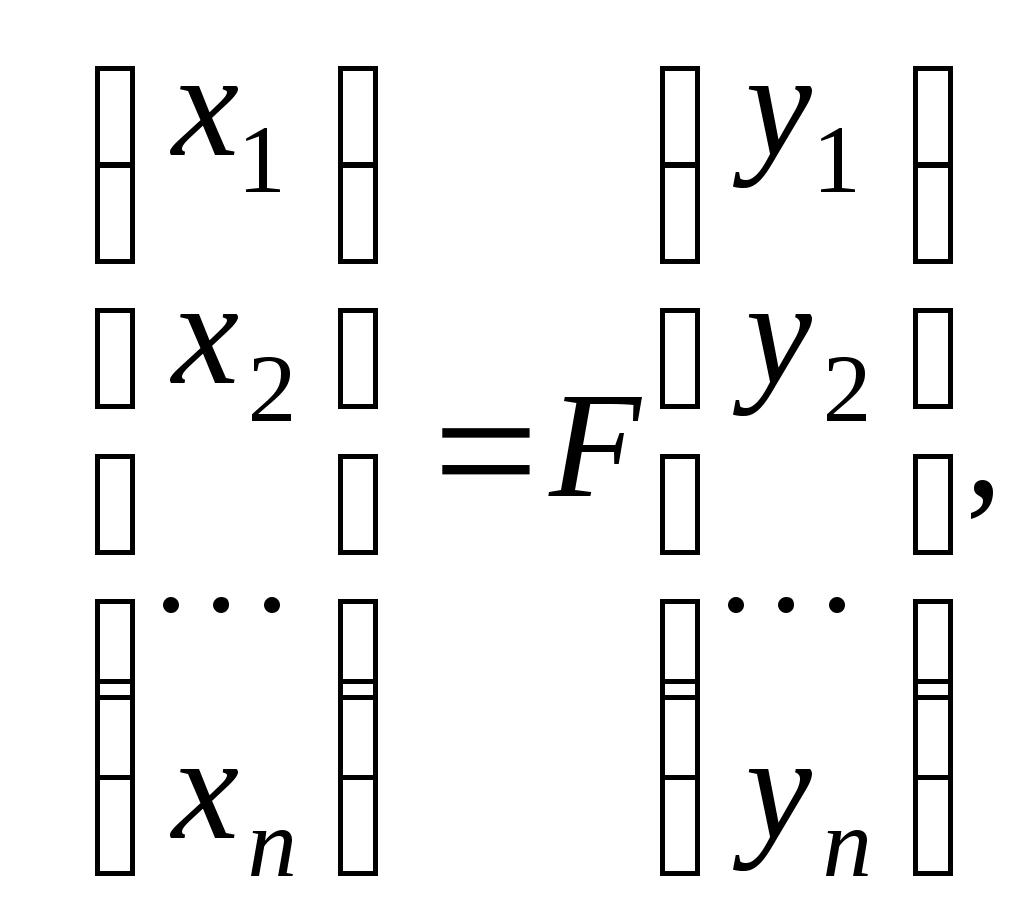
або
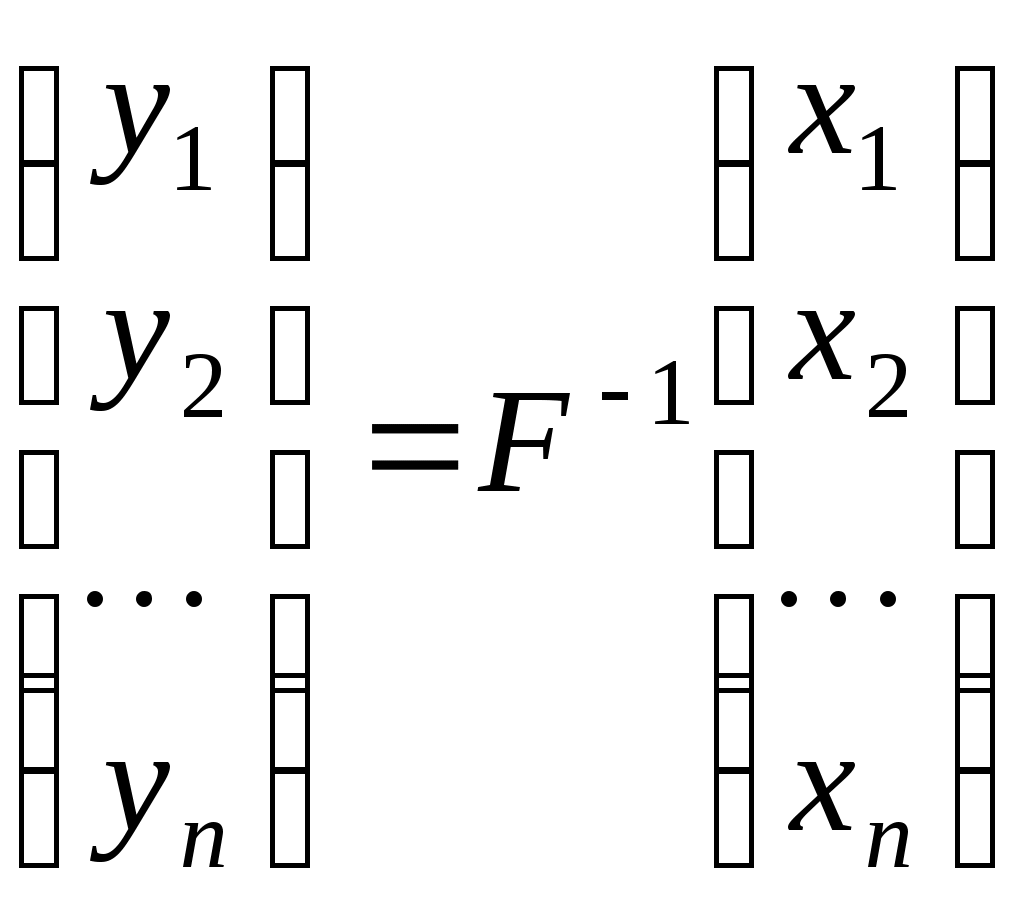 . .
Навпаки, якщо для деякої квадратної матриці  виконується: виконується:
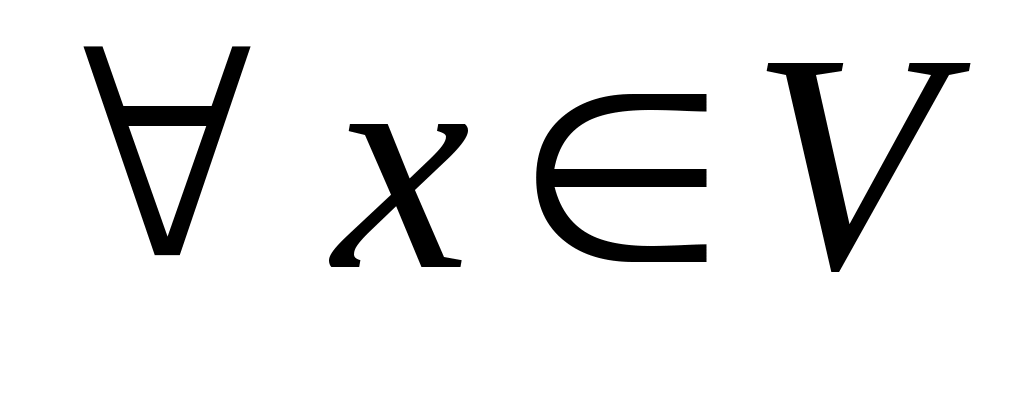 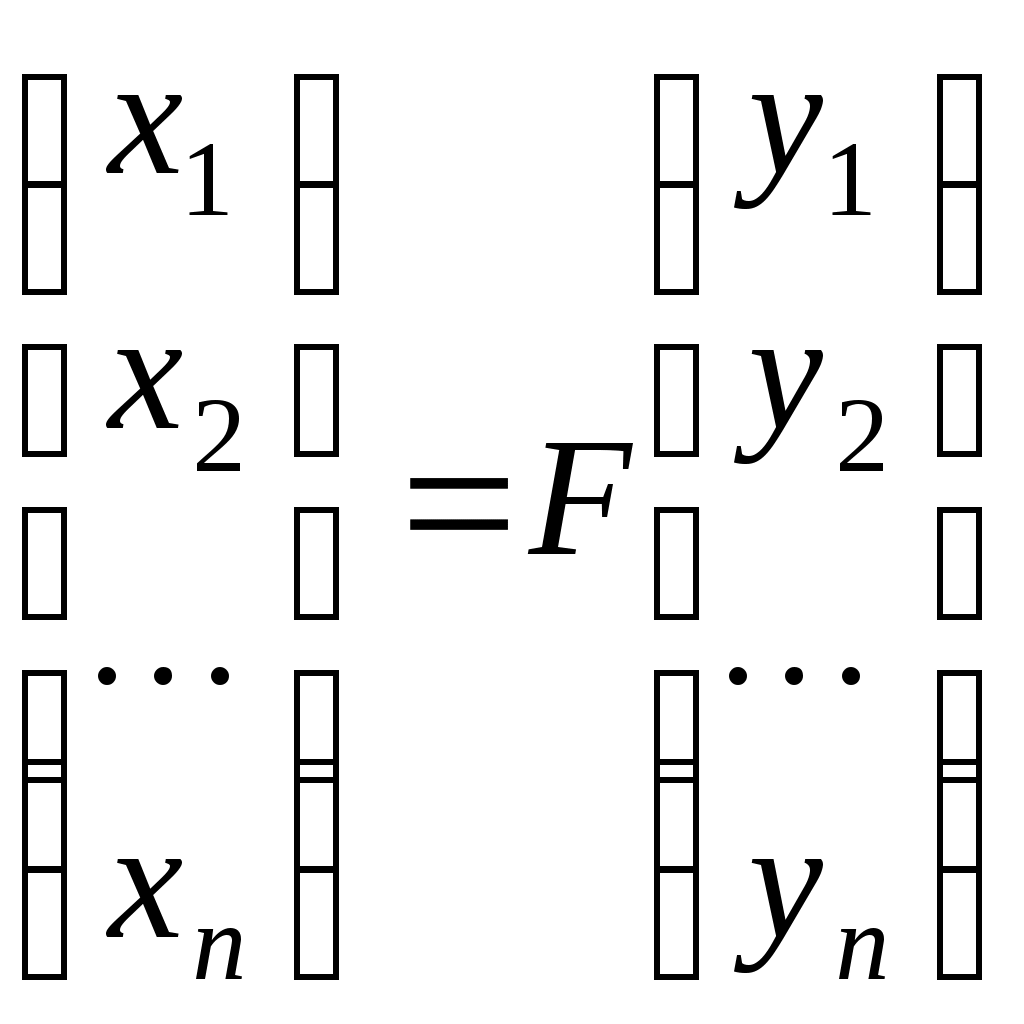 , ,
то  - матриця переходу від базису - матриця переходу від базису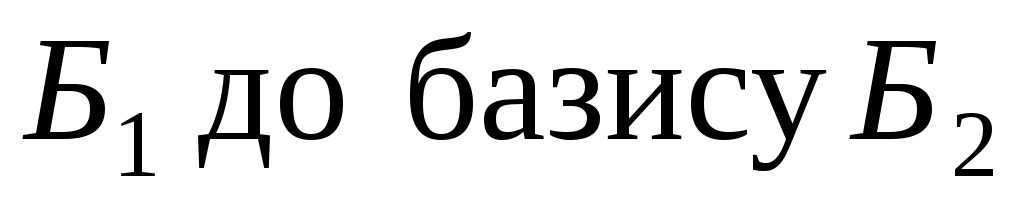 . Дійсно, зафіксуємо індекс . Дійсно, зафіксуємо індекс 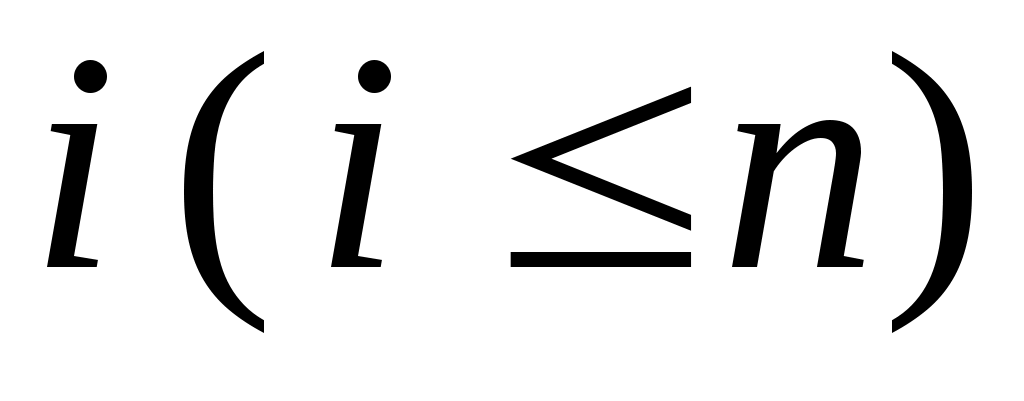 і, оскільки рівність виконується для будь-якого і, оскільки рівність виконується для будь-якого 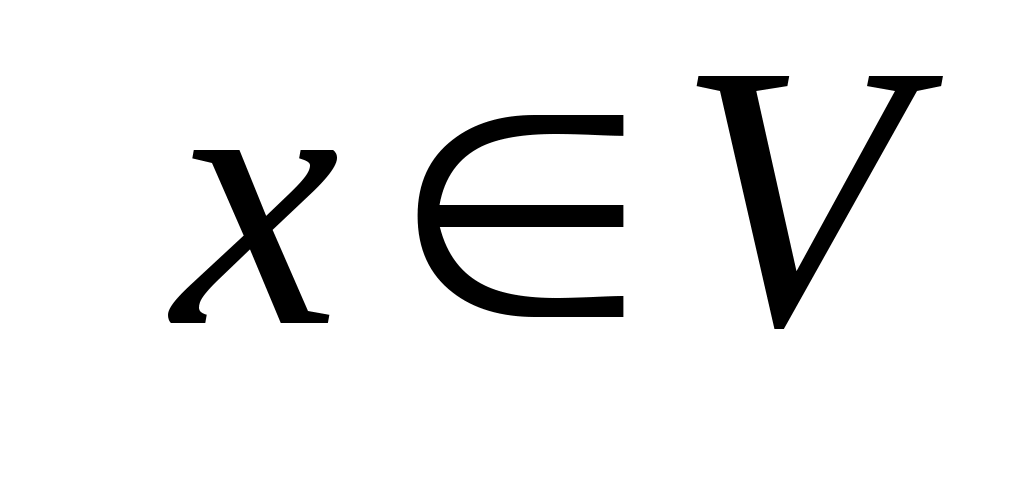 , покладемо , покладемо 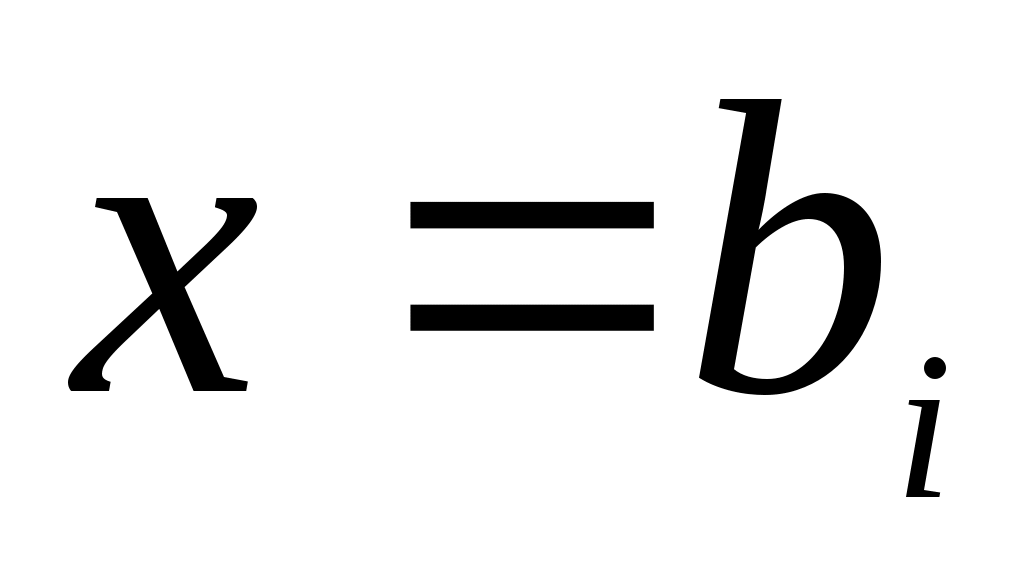 . Тоді вектор . Тоді вектор 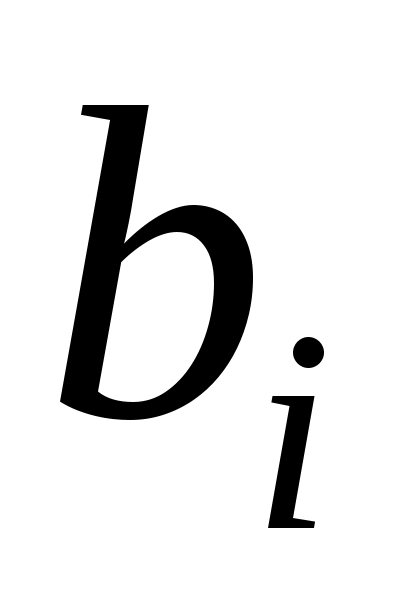 в базисі в базисі 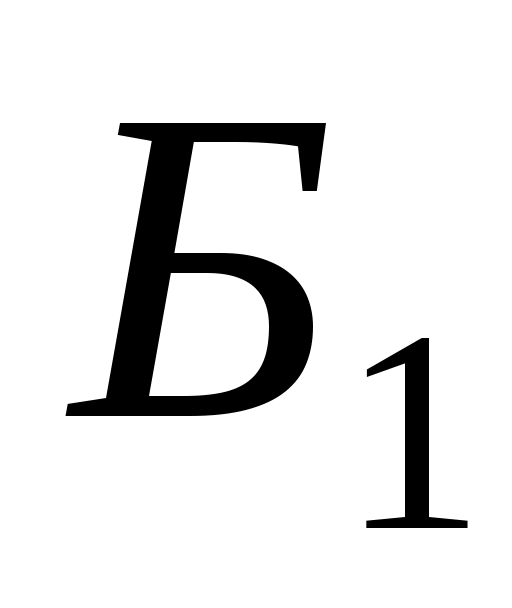 задається такими координатами: задається такими координатами: 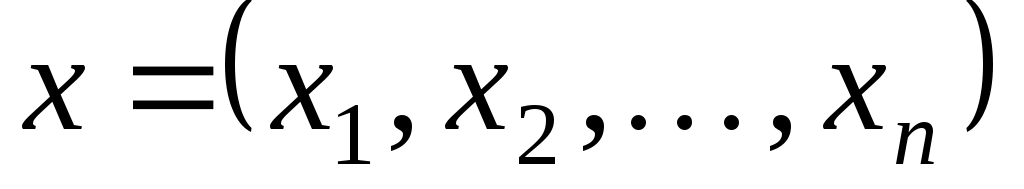 , а в базисі , а в базисі 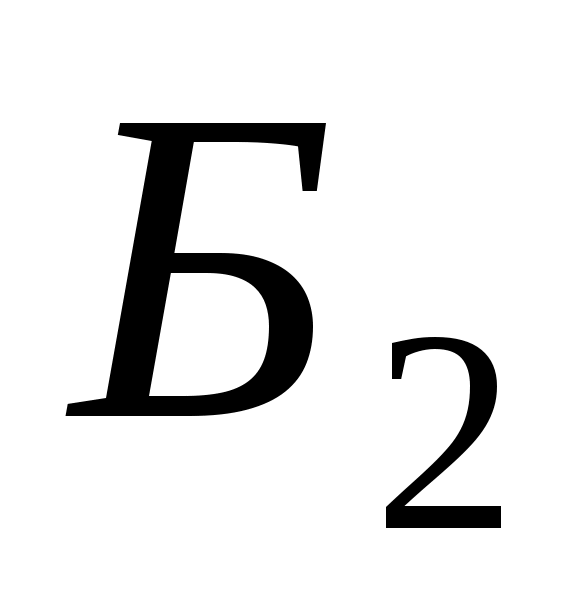 - координатами: - координатами: 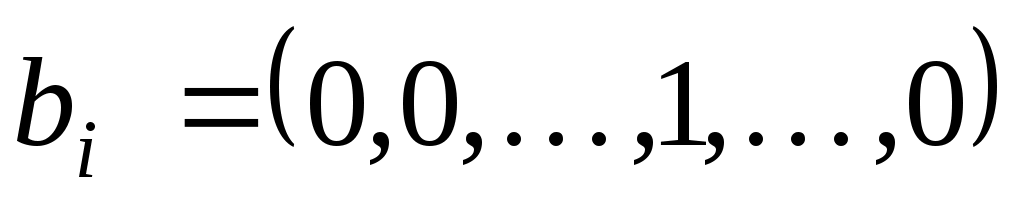 , де координата 1 знаходиться на , де координата 1 знаходиться на 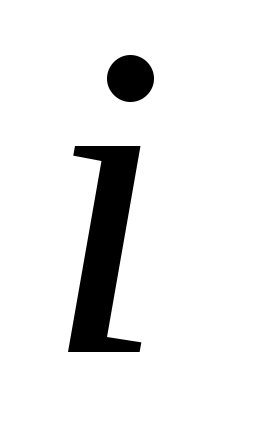 -му місці. Тоді -му місці. Тоді
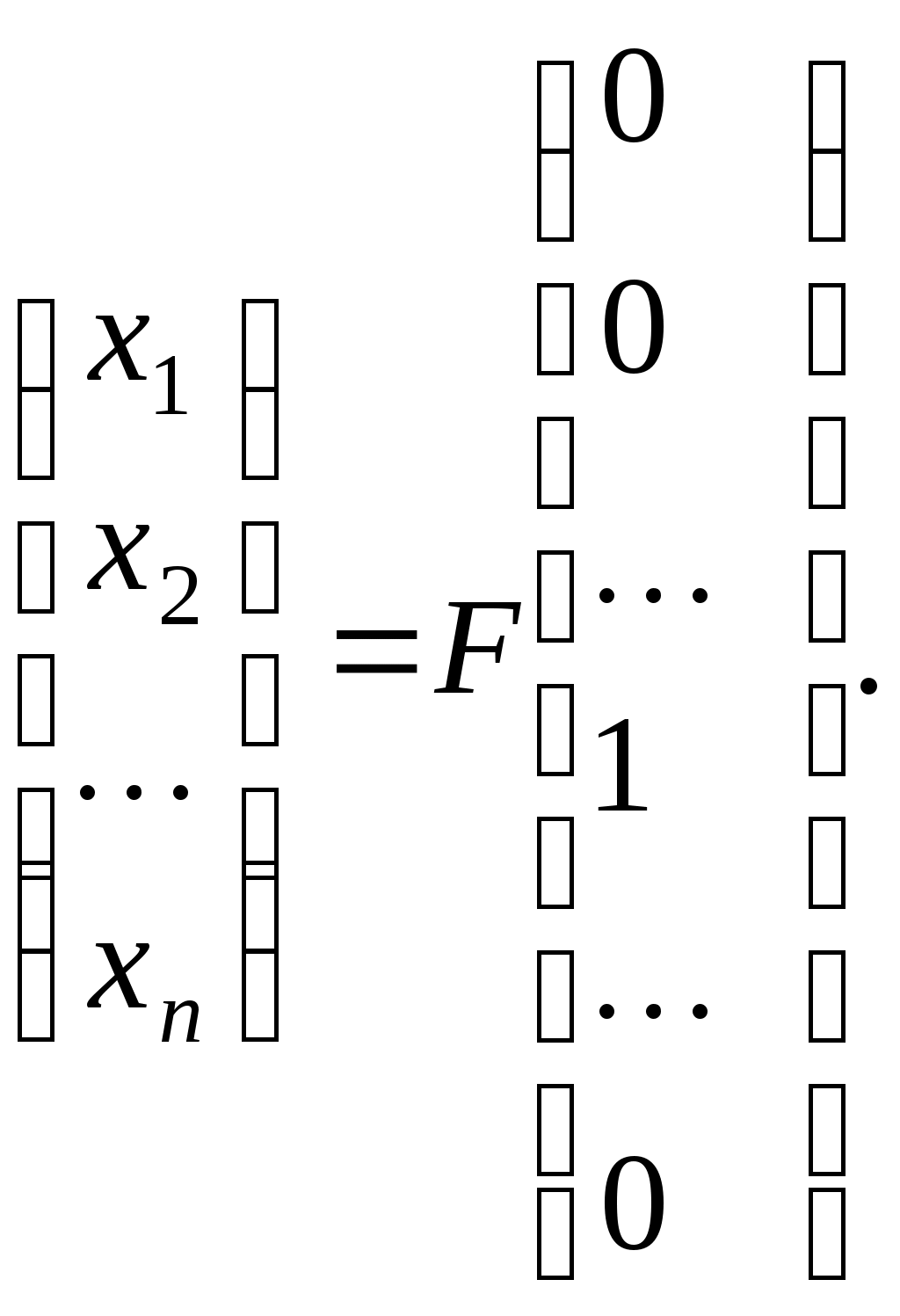
Це означає, що вектор-стовпчик
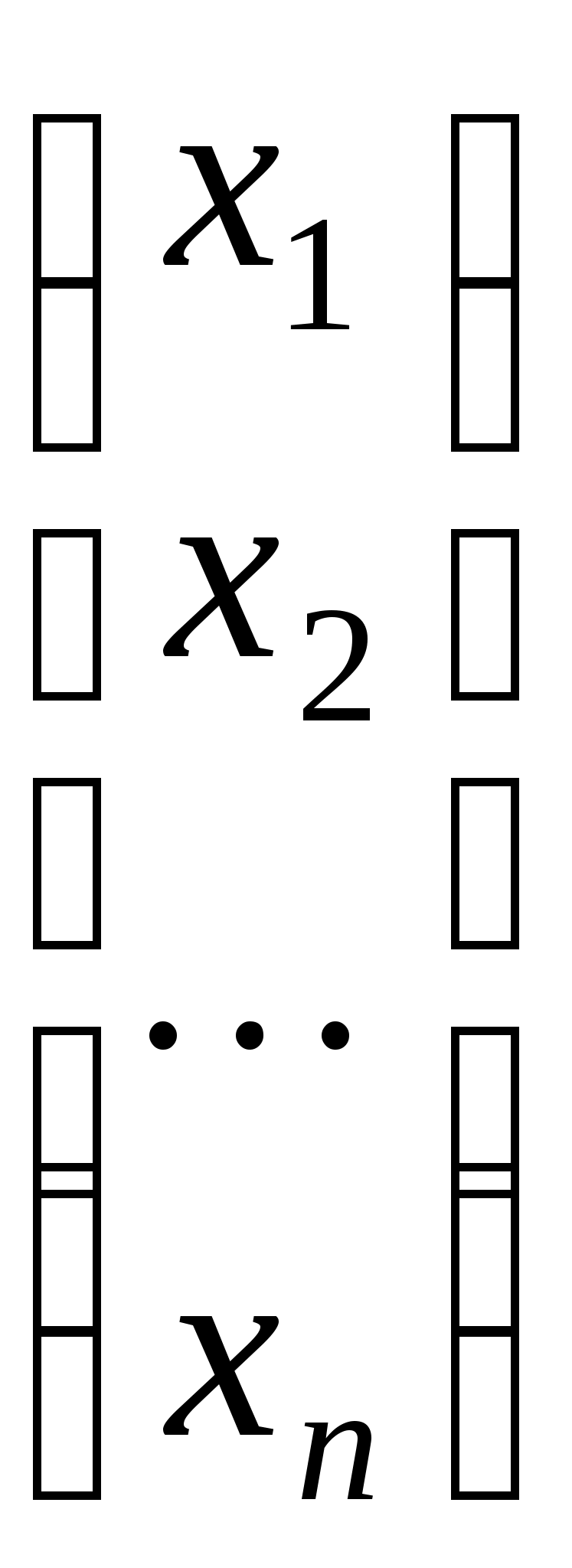
співпадає з 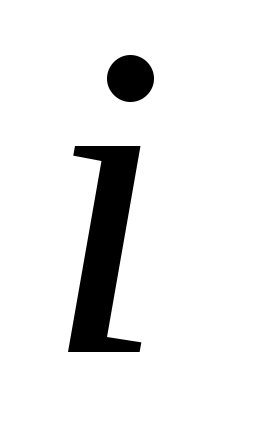 -м стовпчиком матриці -м стовпчиком матриці  . Тобто, матриця . Тобто, матриця  складається з координат складається з координат
векторів  у базисі у базисі 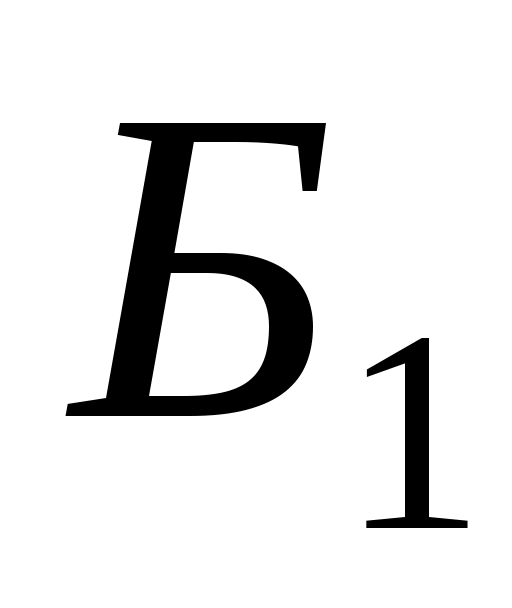 . Отже, матриця . Отже, матриця  є матрицею переходу від базису є матрицею переходу від базису
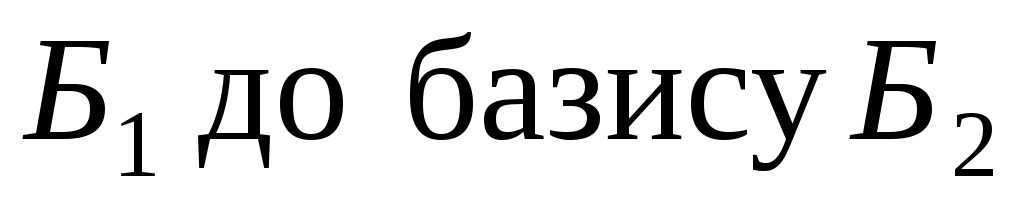 . .
Метод Лагранжа (метод виділення повних квадратів)
Метод Лагранжа є методом зведення квадратичної функції до канонічного вигляду. Він полягає в послідовних виділеннях повних квадратів та замінах змінних. Кожна заміна змінних означає перехід до нового базису.
Нехай квадратична функція 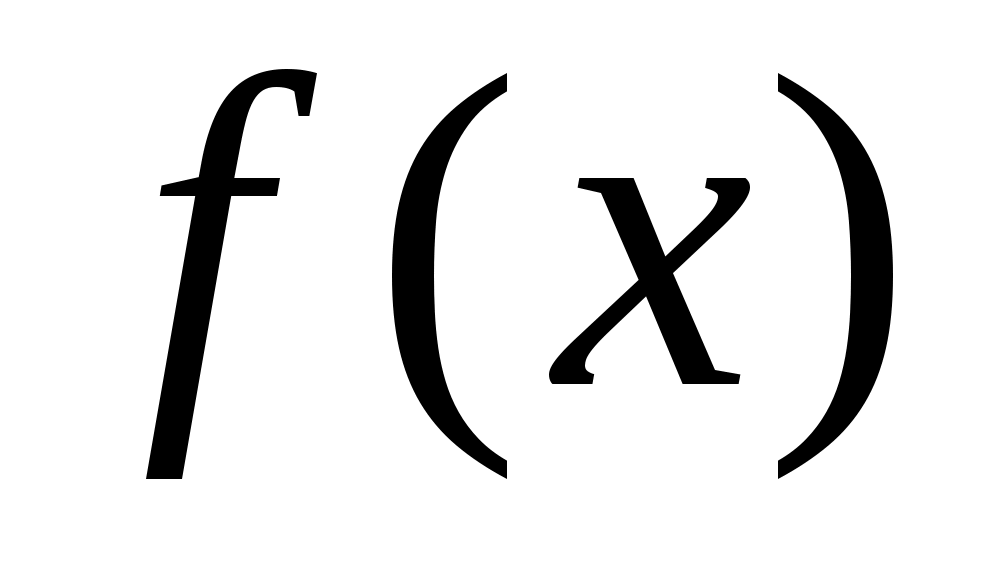 на скінченновимірному просторі на скінченновимірному просторі  у базисі у базисі 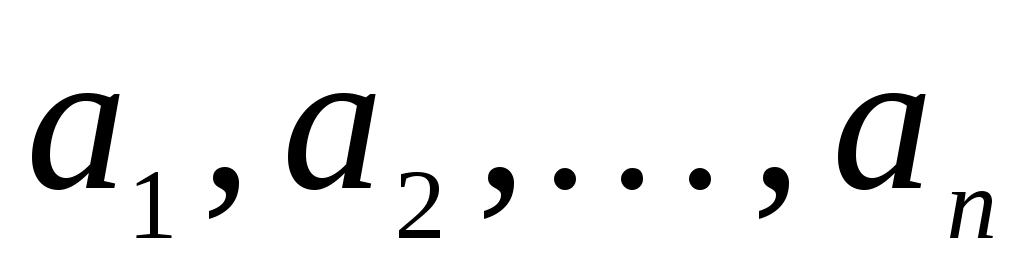 задається квадратичною формою: задається квадратичною формою:
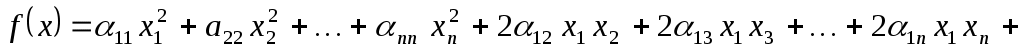
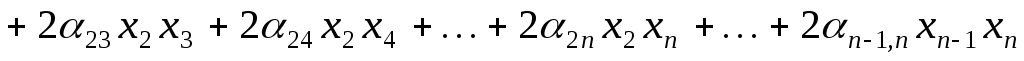 , ,
і припустимо, що 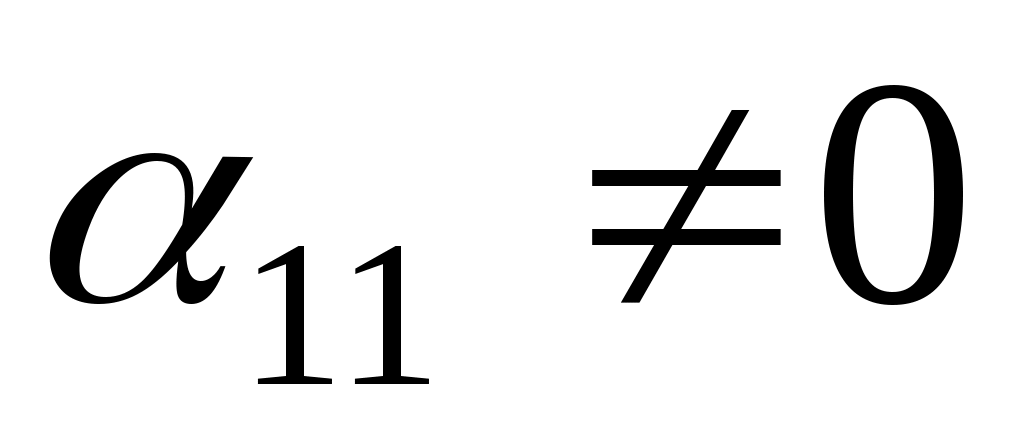 . В дужках збираємо всі доданки, що містять змінну . В дужках збираємо всі доданки, що містять змінну 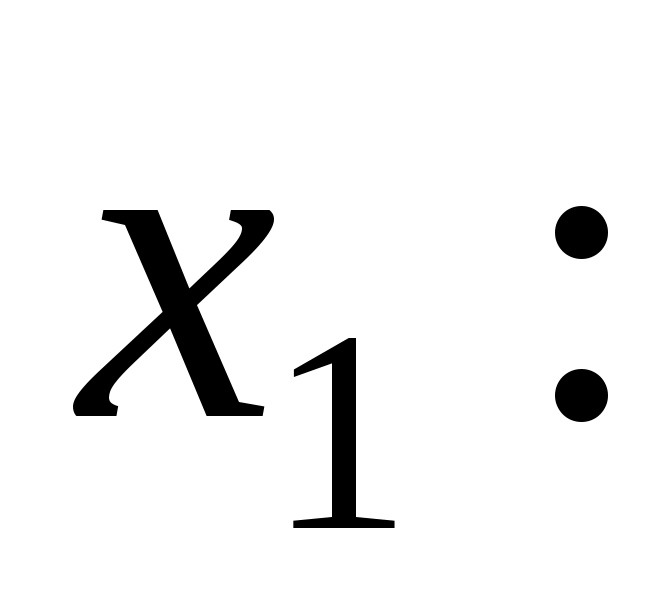
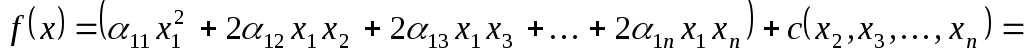
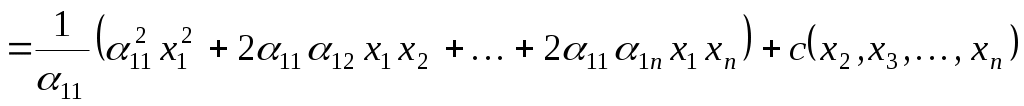 , ,
де 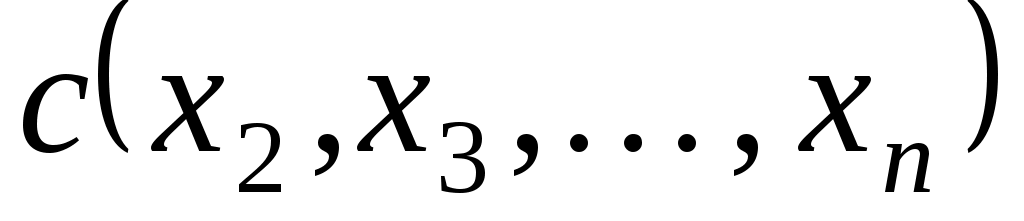 - деяка квадратична форма від змінних - деяка квадратична форма від змінних 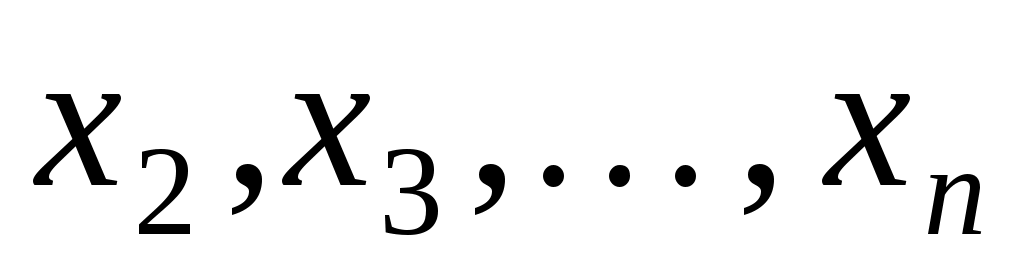 . У дужках виділяємо повний квадрат: . У дужках виділяємо повний квадрат:
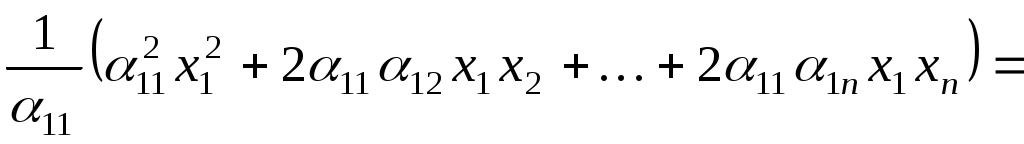 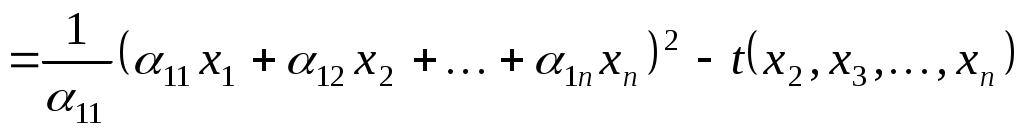 , ,
де 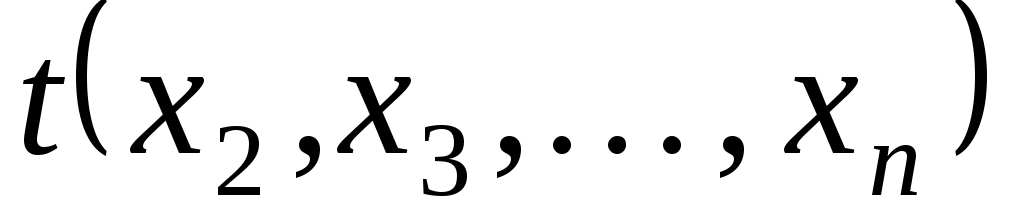 - сума всіх доданків, які не містять змінну - сума всіх доданків, які не містять змінну 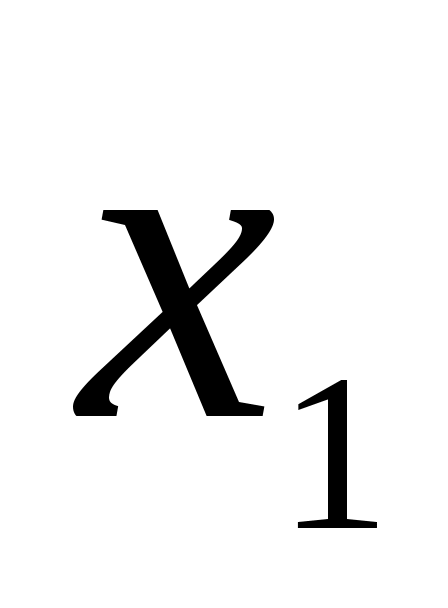 . Тоді . Тоді
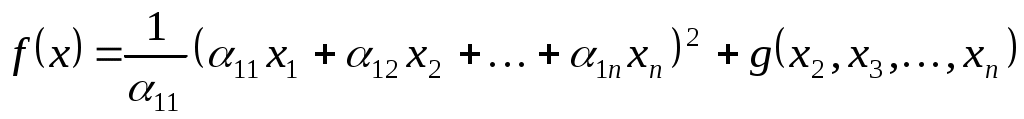 , ,
де 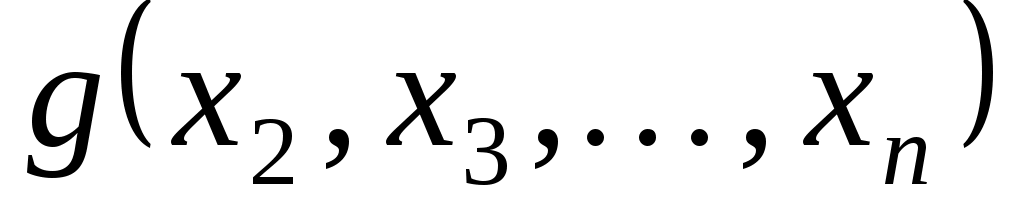 - квадратична форма від змінних - квадратична форма від змінних 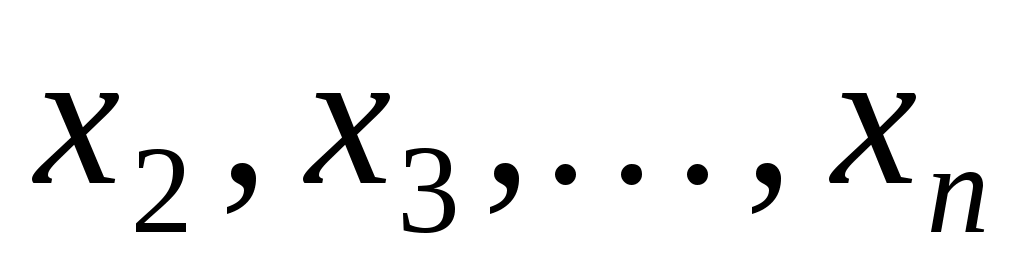 . Зробимо заміну змінних: . Зробимо заміну змінних:
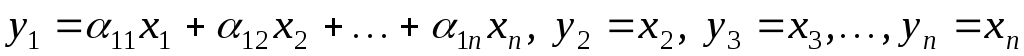 . .
Або, в матричному вигляді,
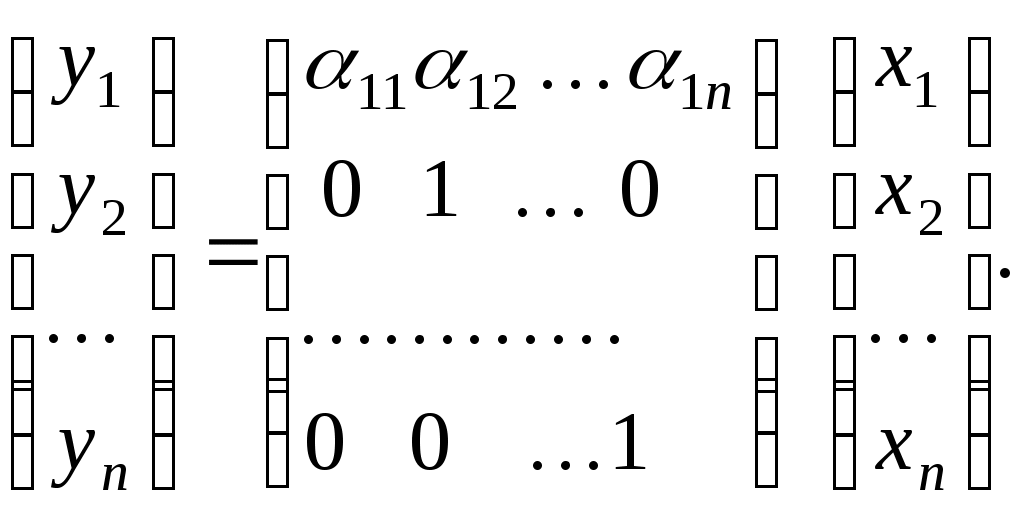
Позначимо
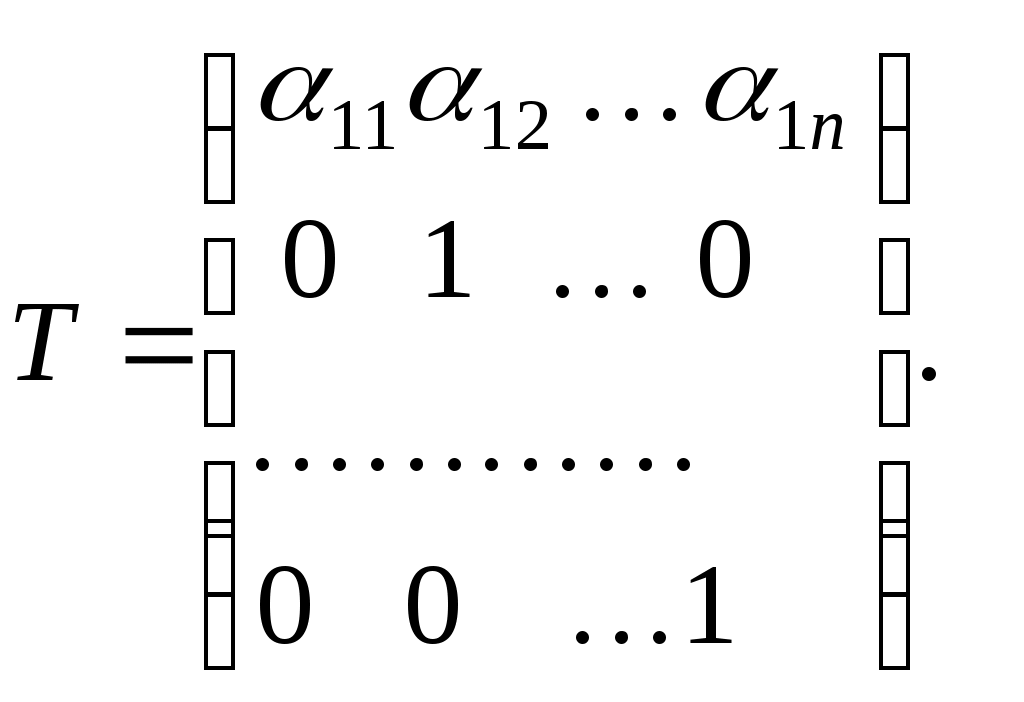
Матриця 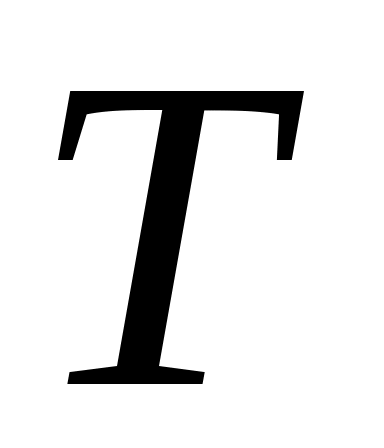 невироджена, оскільки невироджена, оскільки 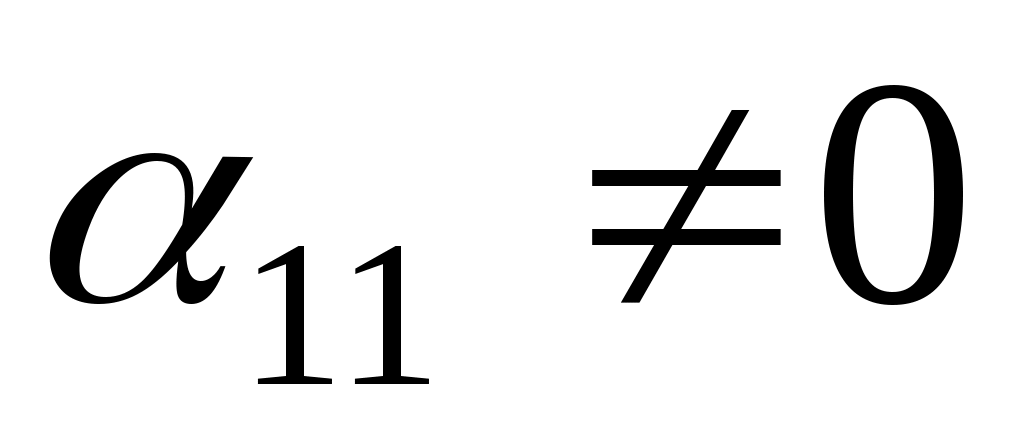 . .
З’ясуємо зміст цієї заміни. Заміна змінних означає перехід до нового базису 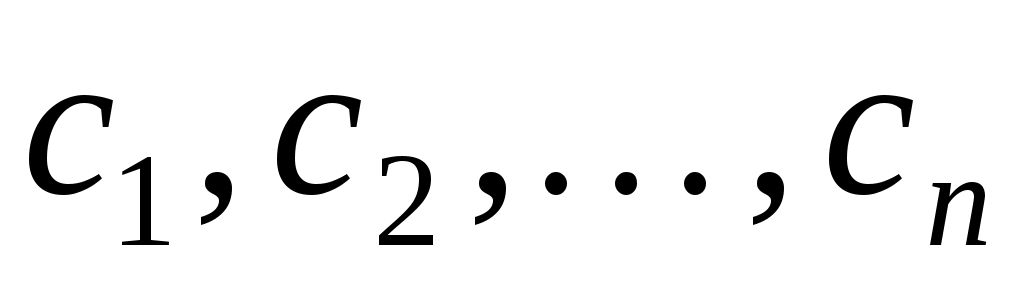 , причому, якщо вектор , причому, якщо вектор  у базисі у базисі  задається координатами задається координатами 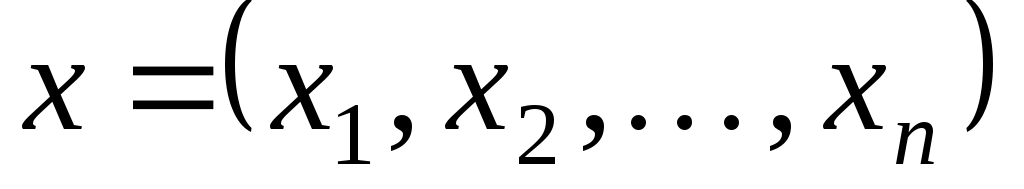 , а в базисі , а в базисі 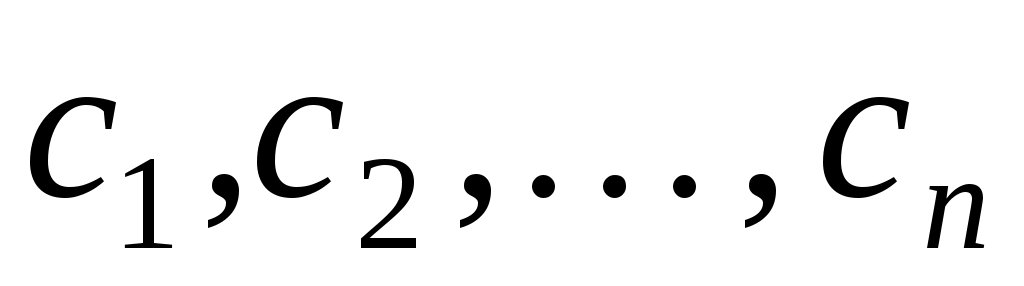 - координатами - координатами 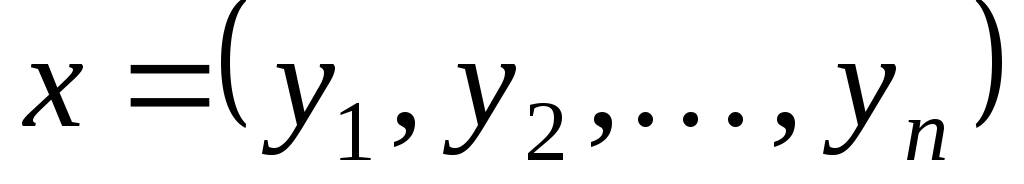 , то , то
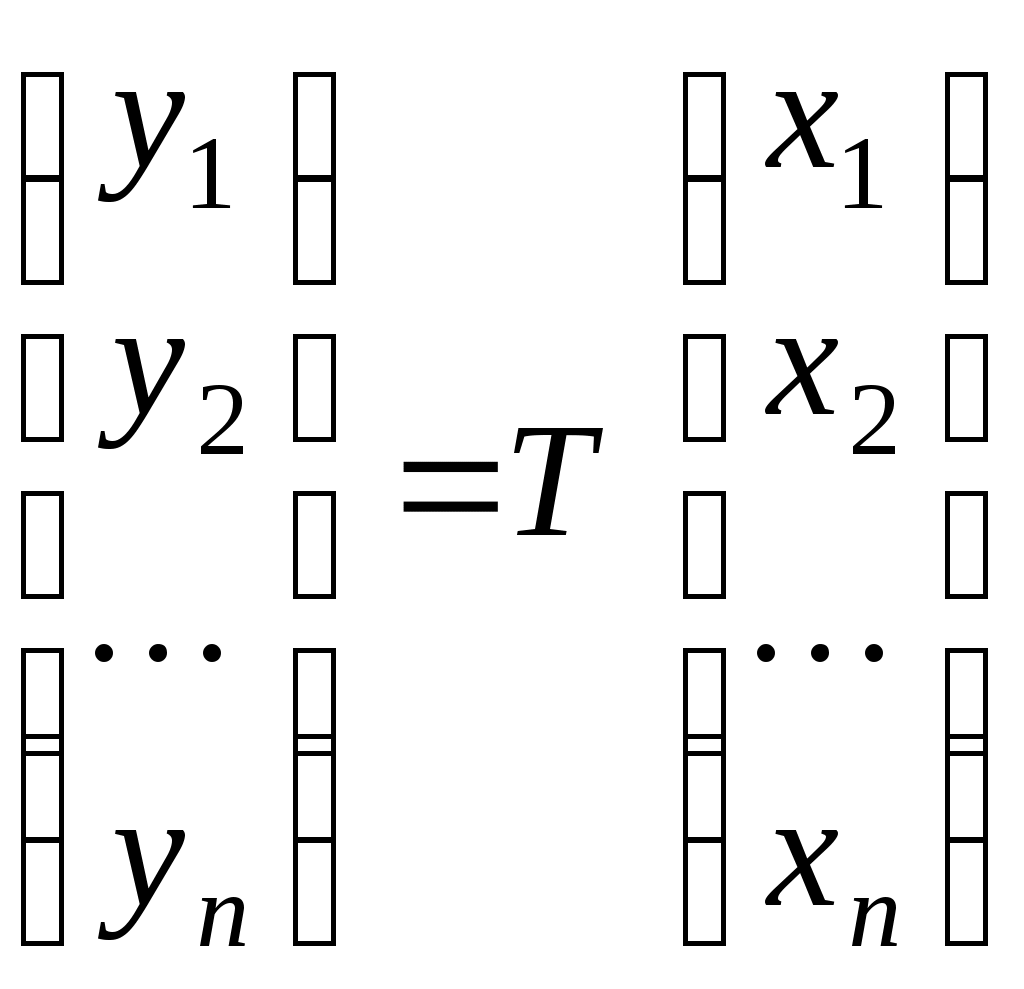 , ,
або
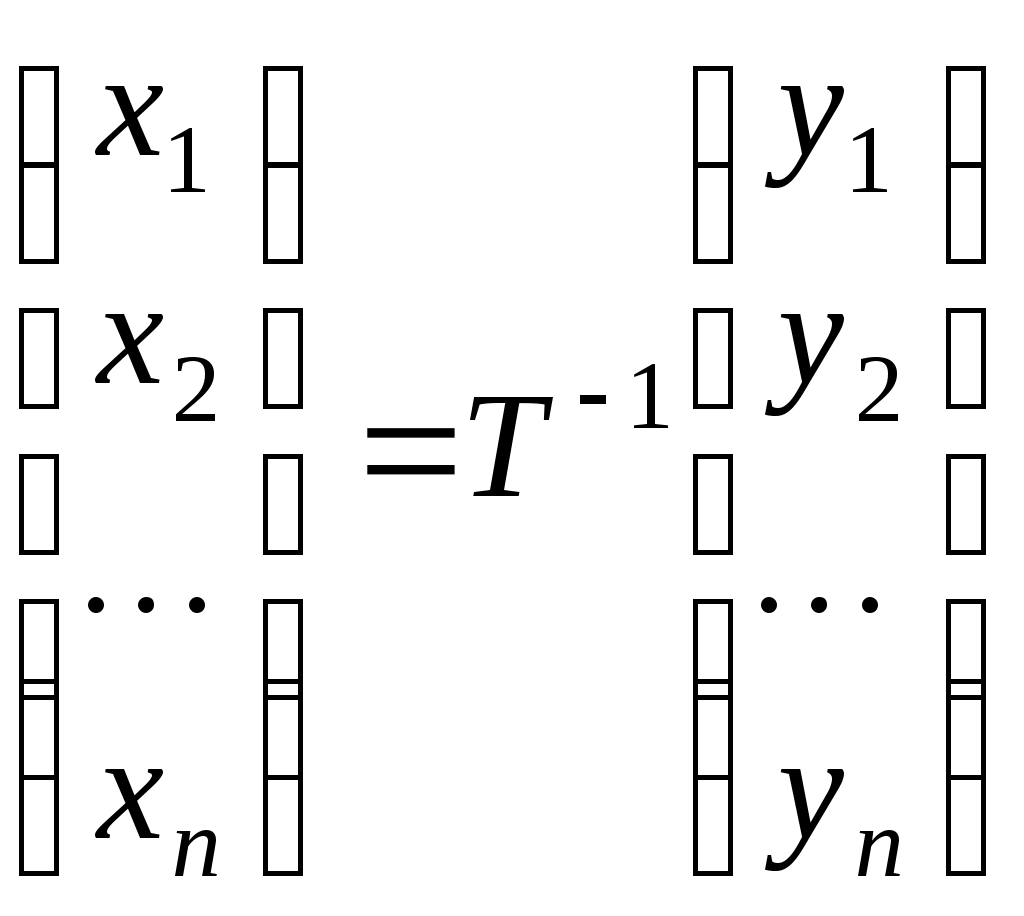 . .
Таким чином, 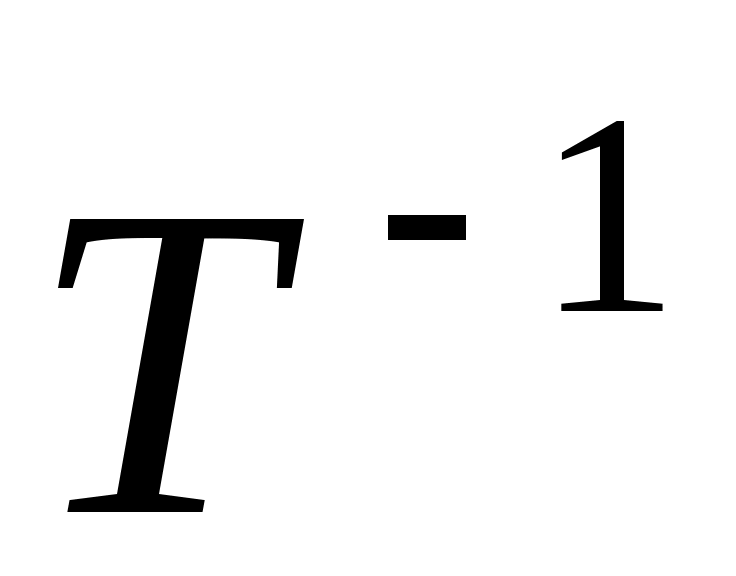 - матриця переходу від базису - матриця переходу від базису 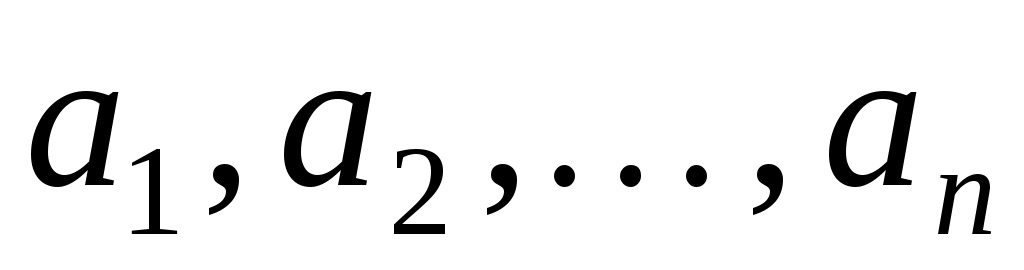 до базису до базису 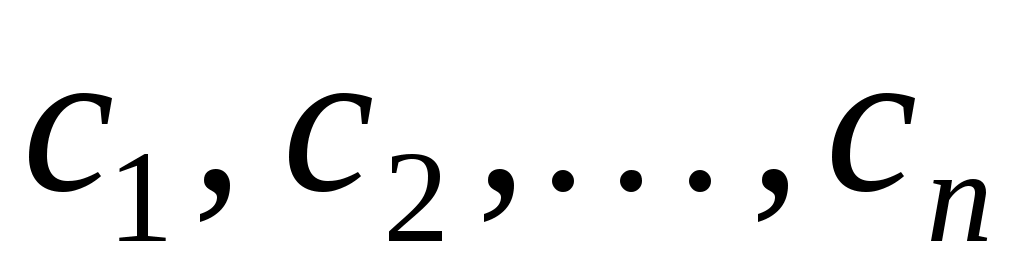 . .
У новому базисі квадратична функція задається квадратичною формою:
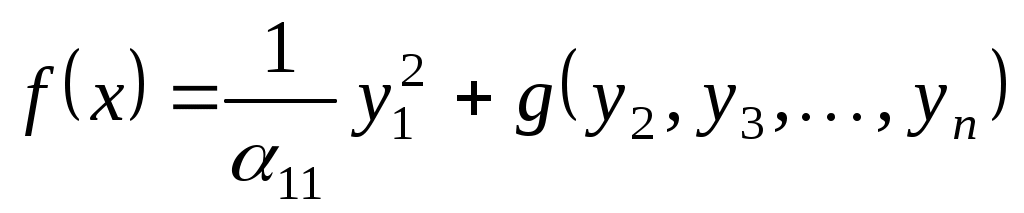 . .
Далі застосовуємо аналогічні міркування для квадратичної форми 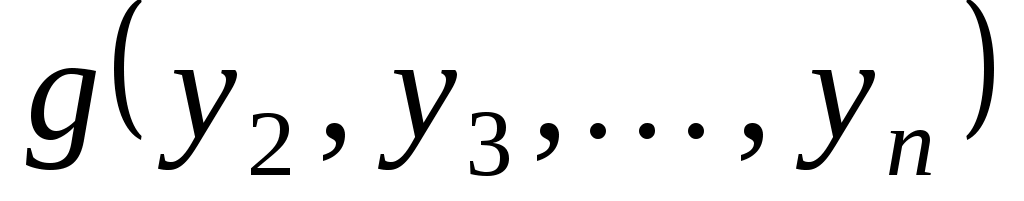 . .
Припустимо, що в початковій квадратичній формі 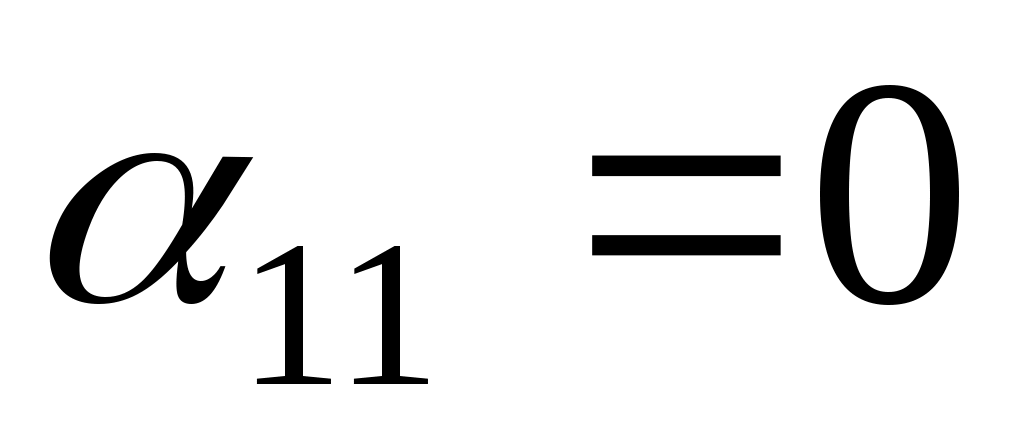 , але для деякого , але для деякого 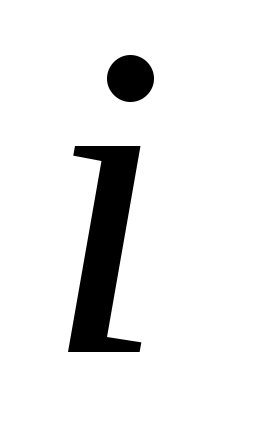 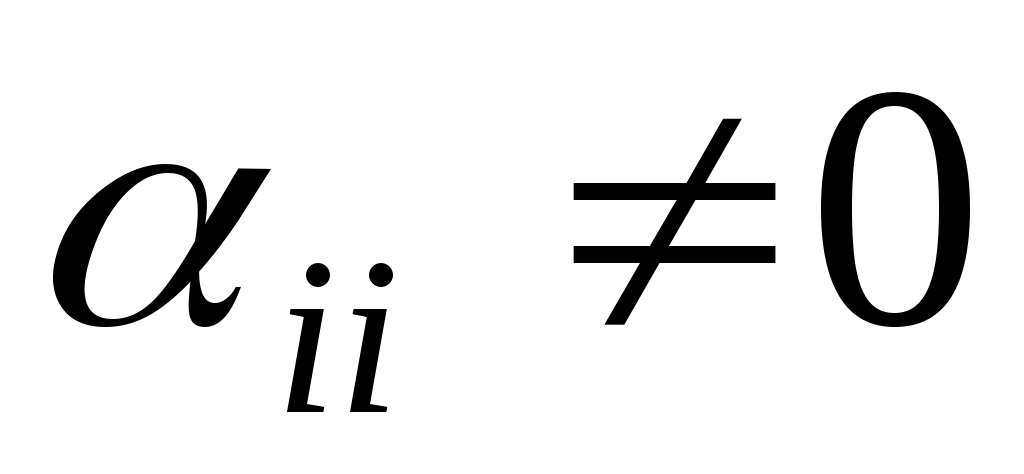 .Тоді використовуємо аналогічні міркування для змінної .Тоді використовуємо аналогічні міркування для змінної 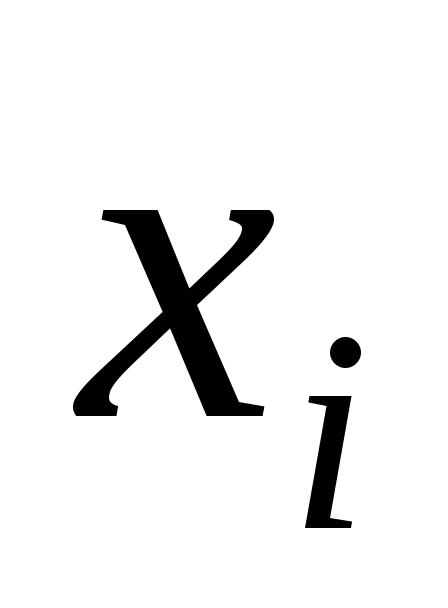 . .
Окремо розглянемо випадок, коли в початковій квадратичній формі немає квадратів змінних, тобто,
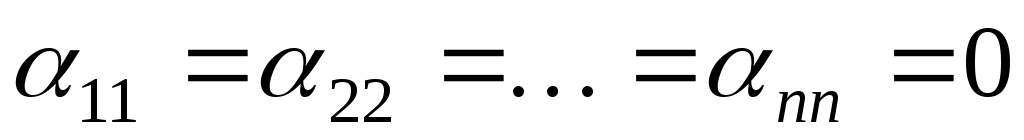 . .
Тоді форма складається лише з мішаних добутків змінних і для деякої пари індексів 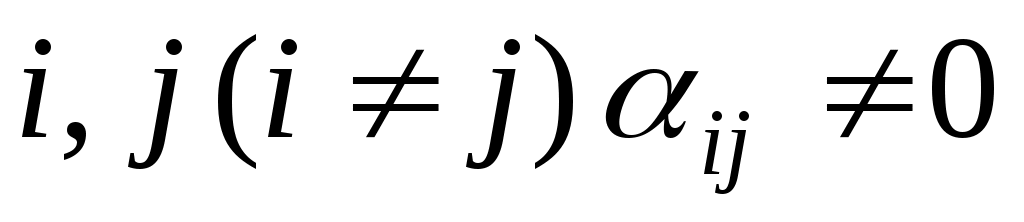 . Припустимо для визначеності, що . Припустимо для визначеності, що 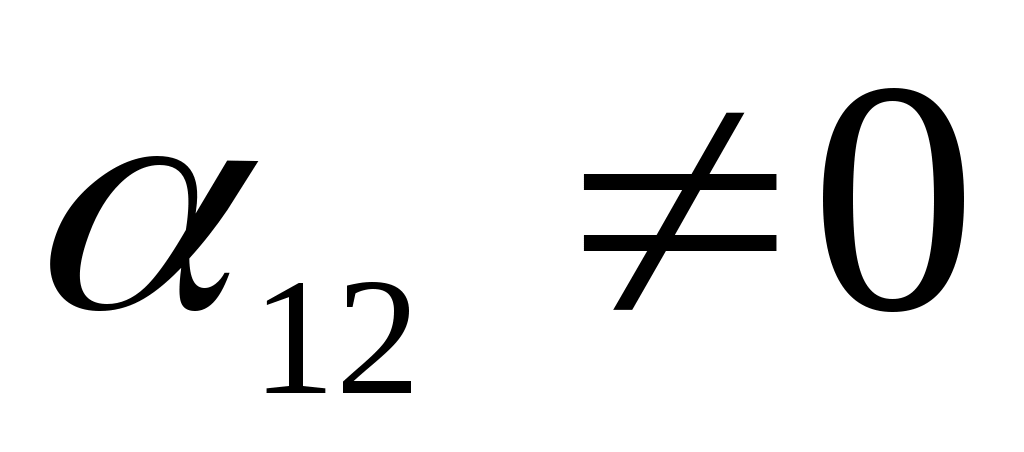 , і зробимо заміну змінних: , і зробимо заміну змінних:
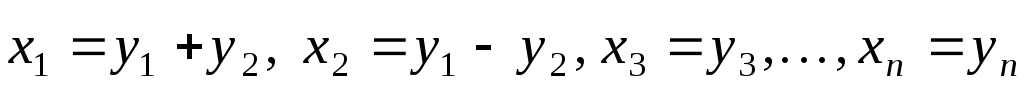 . .
У матричному вигляді:
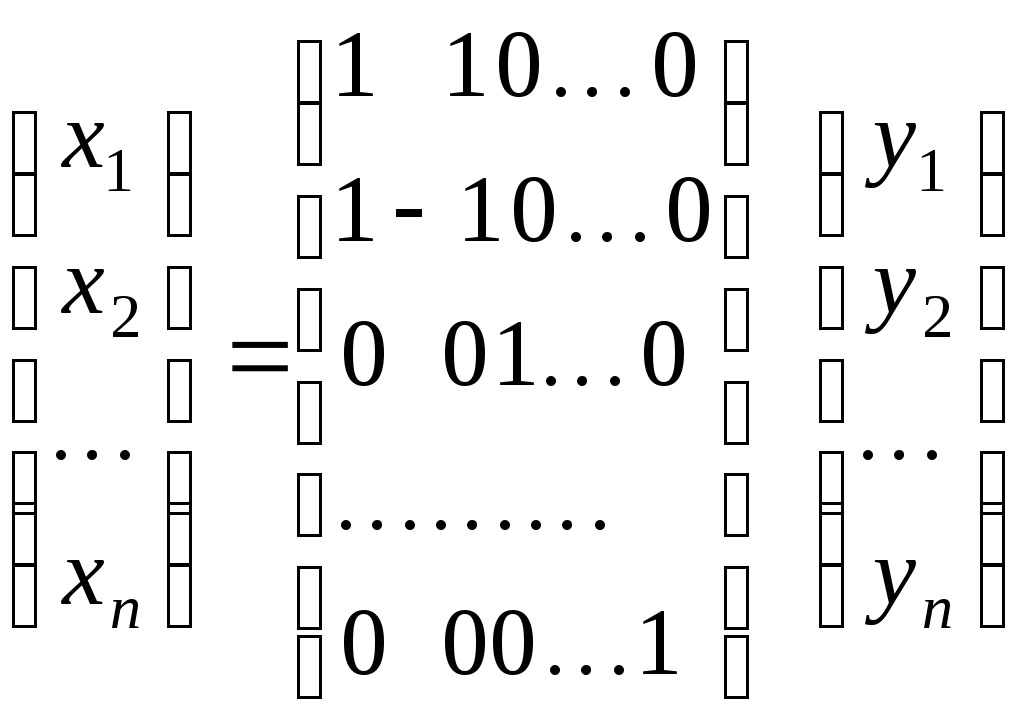 . .
Позначимо
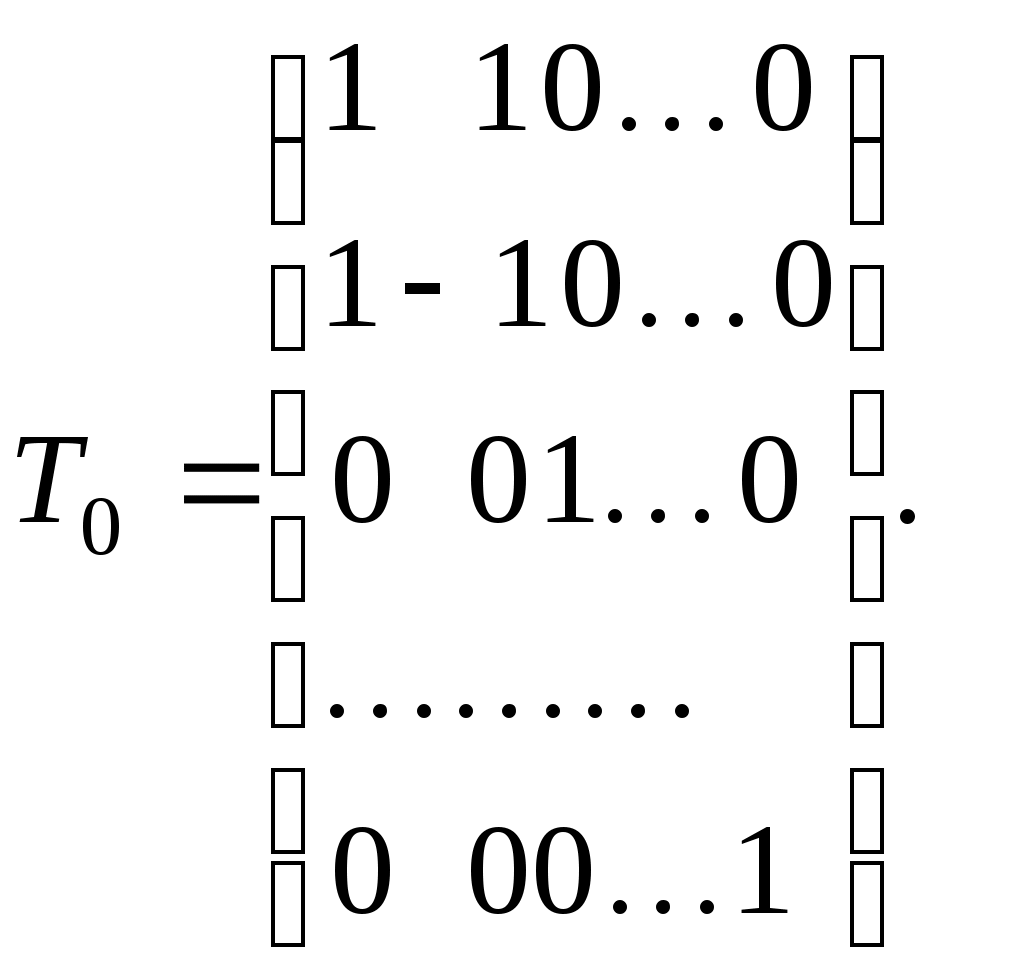
Заміна змінних означає перехід від початкового базису  до нового базису до нового базису 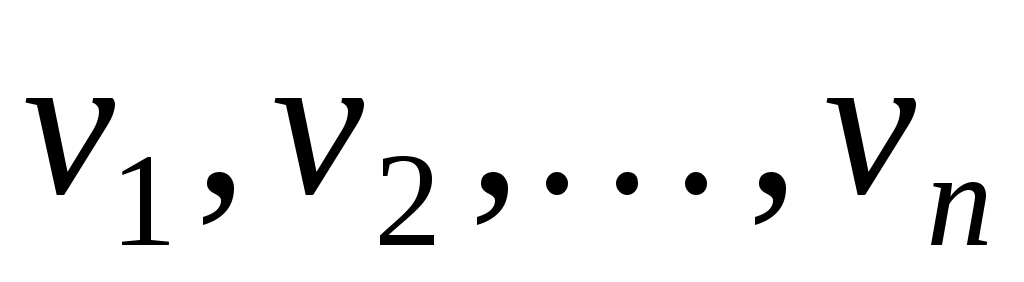 , причому, якщо вектор , причому, якщо вектор  у базисі у базисі  задається координатами: задається координатами: 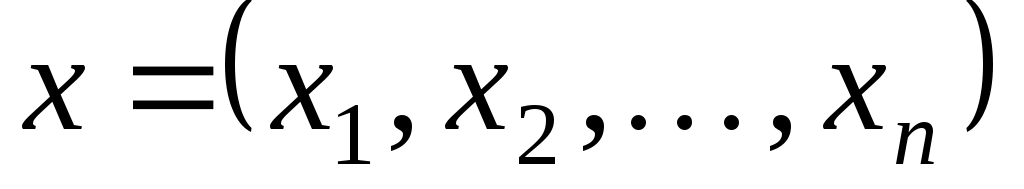 , а в базисі , а в базисі 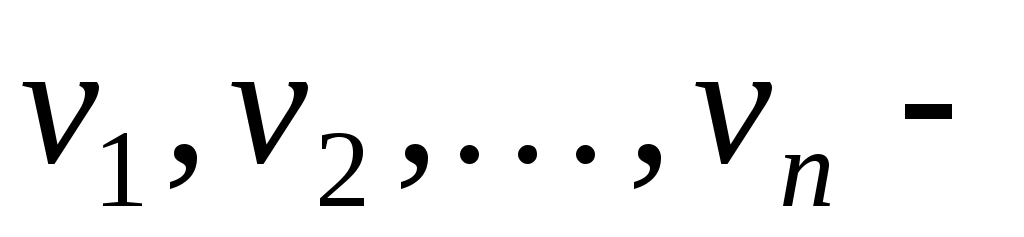 координатами: координатами: 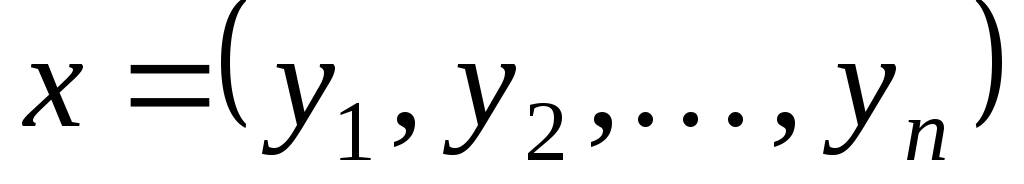 , то , то
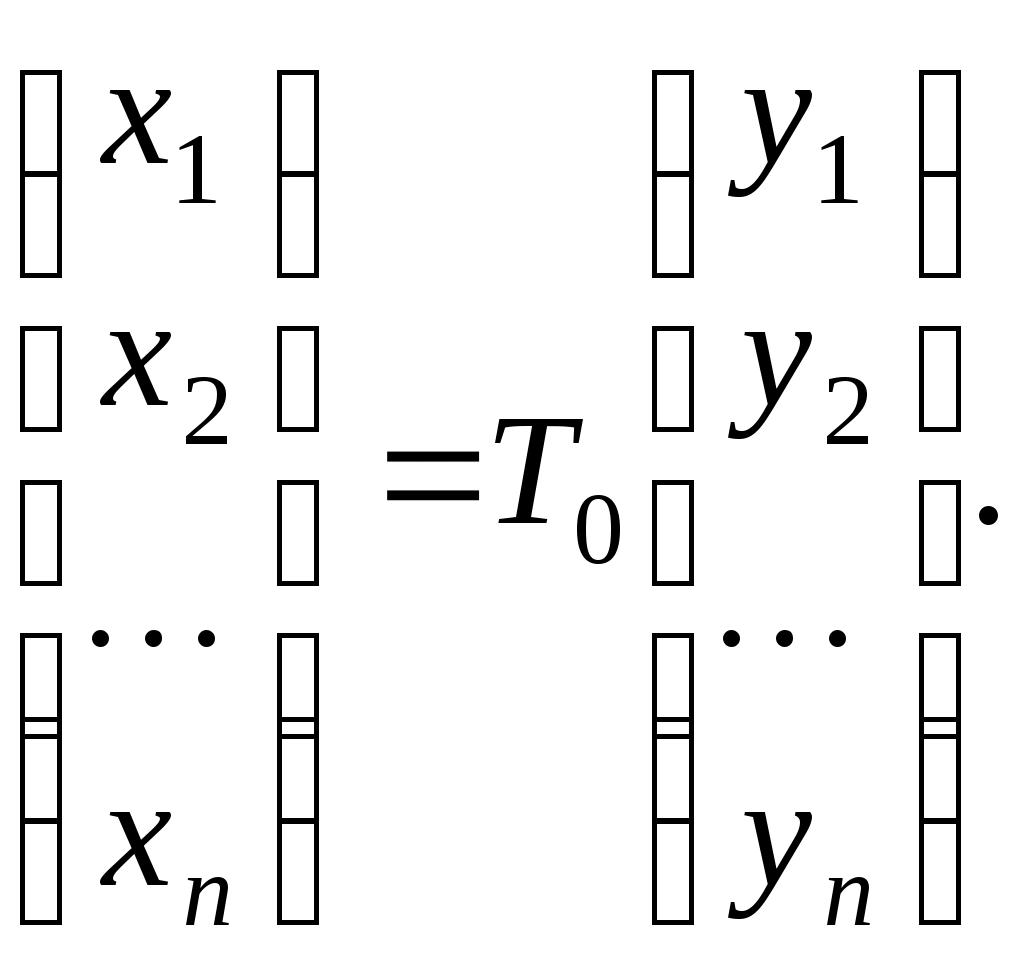
Тобто, 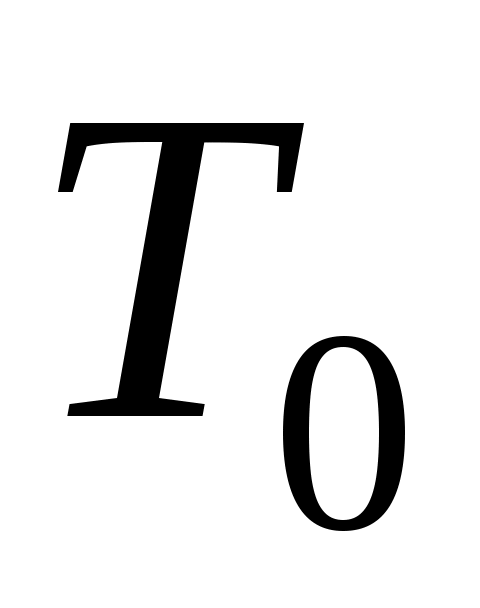 - матриця переходу від базису - матриця переходу від базису 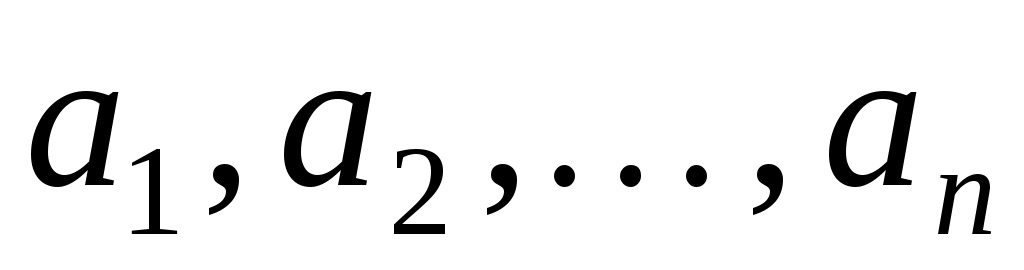 до базису до базису 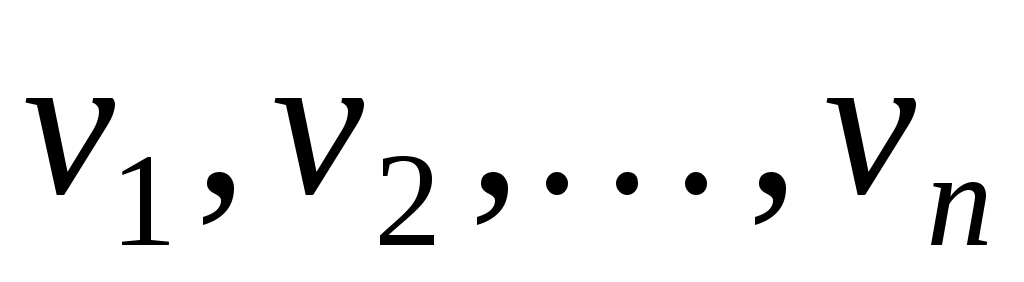 . .
У новому базисі квадратична функція задається квадратичною формою:
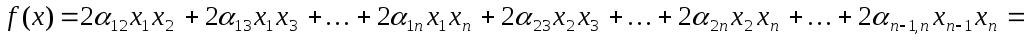 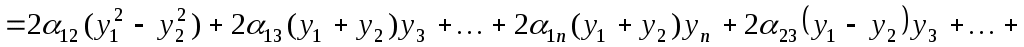
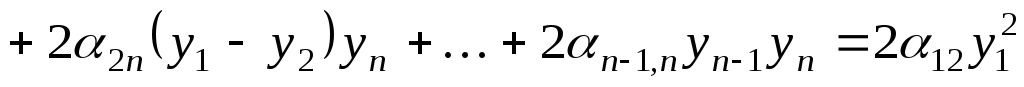 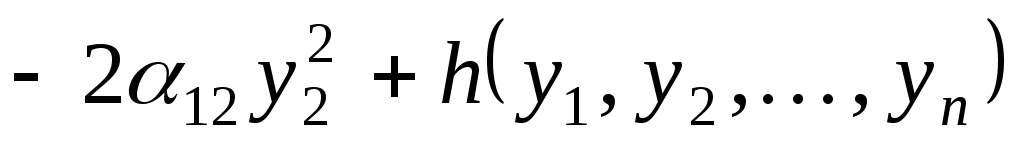 , ,
де квадратична форма 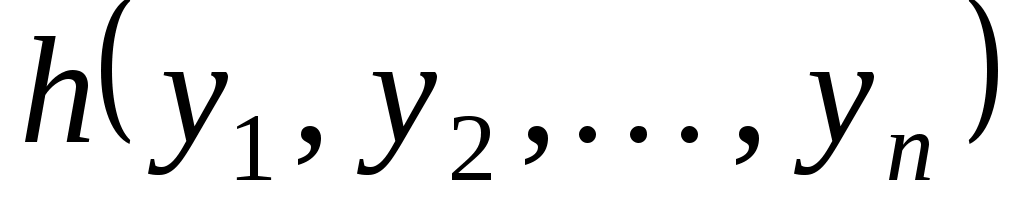 складається лише з мішаних добутків змінних. складається лише з мішаних добутків змінних.
Продовжуючи цей процес далі, через 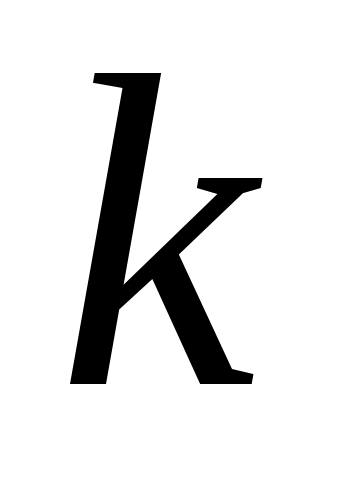 кроків приходимо до базису простору кроків приходимо до базису простору  , у якому квадратична функція , у якому квадратична функція 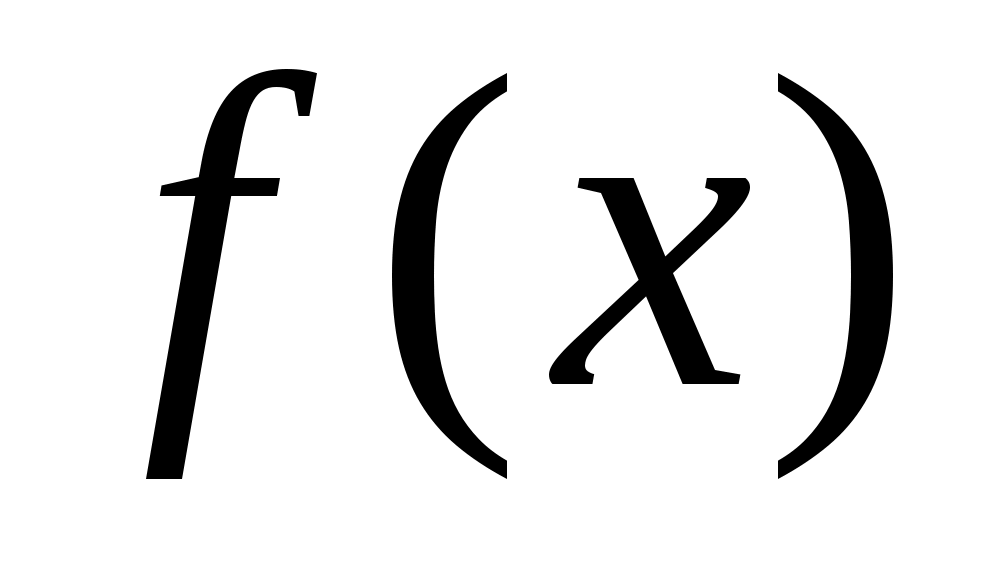 задається канонічною квадратичною формою: задається канонічною квадратичною формою:
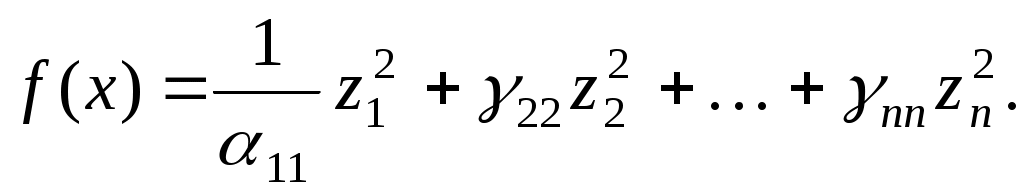
Кожний крок алгоритму означає перехід до нового базису. Нехай 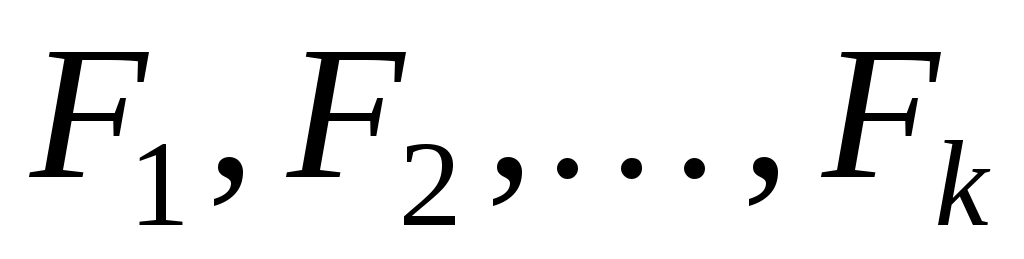
- відповідні матриці переходу. Тоді для початкових та заключних змінних виконується рівність:
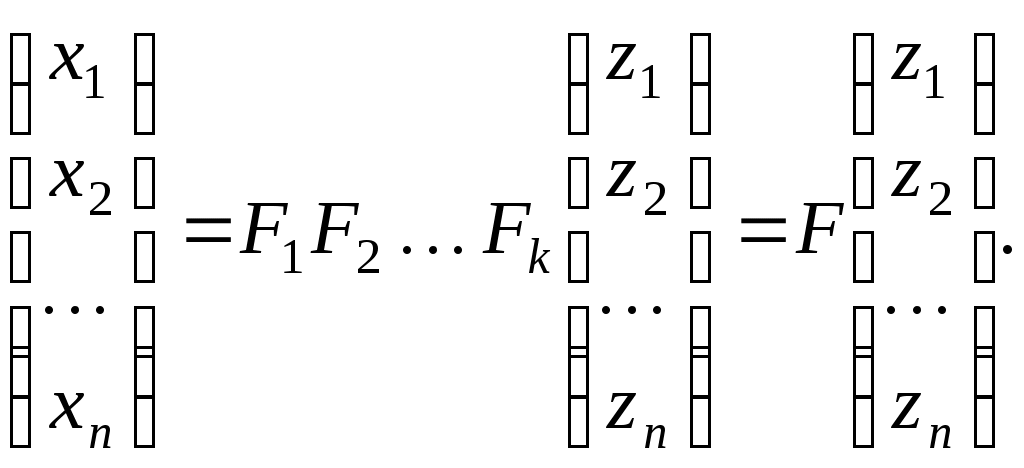
Це означає, що матриця 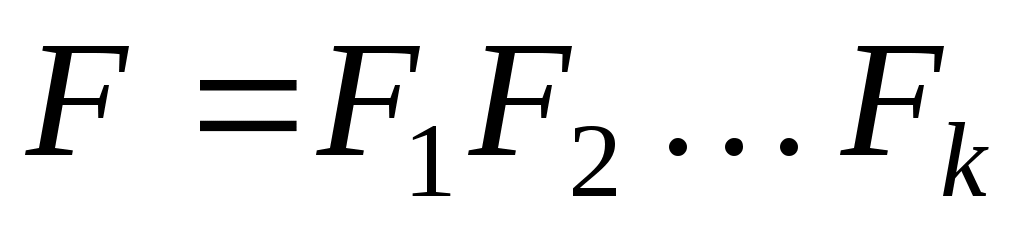 є матрицею переходу від початкового базису є матрицею переходу від початкового базису
 до заключного базису до заключного базису  . .
|
|
|
 Скачать 1.43 Mb.
Скачать 1.43 Mb.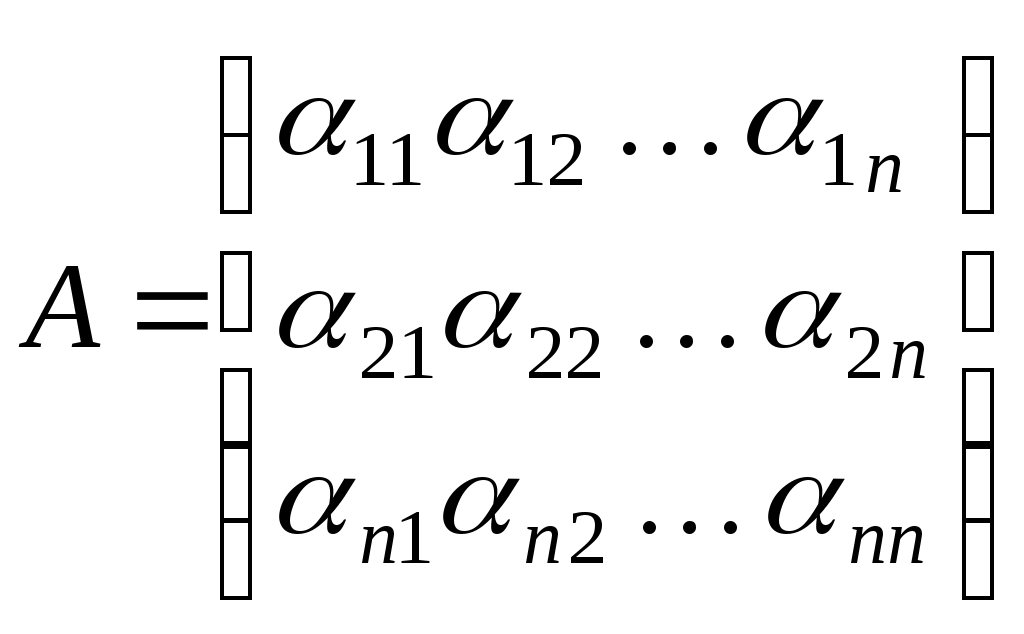 .
.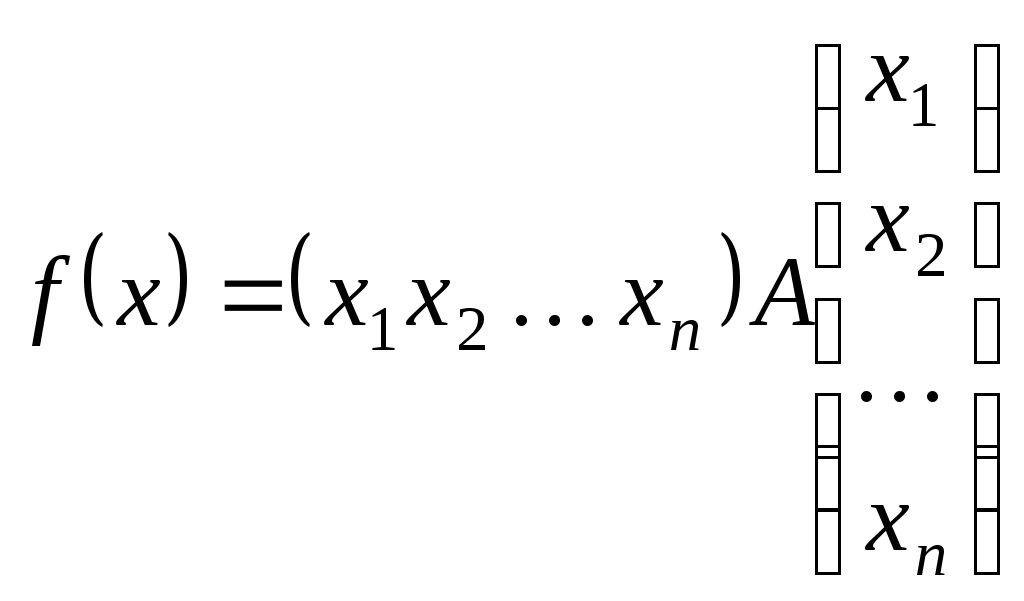 .
.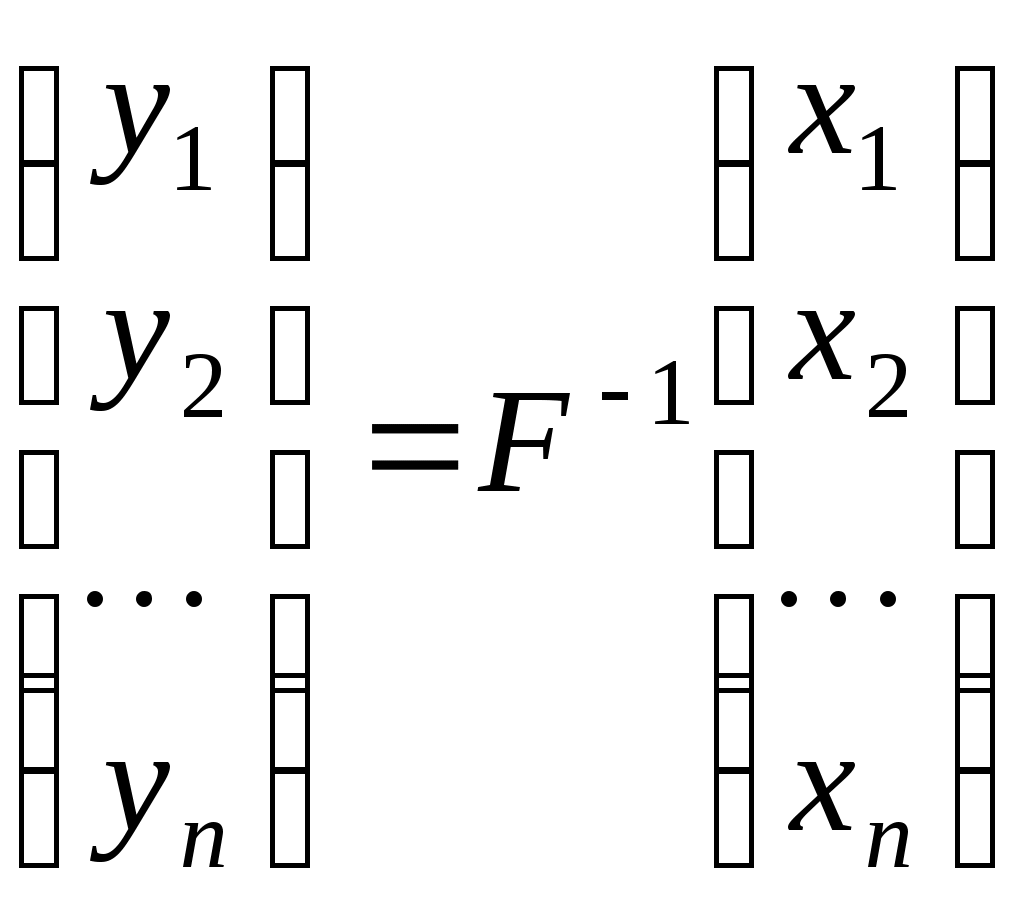 .
.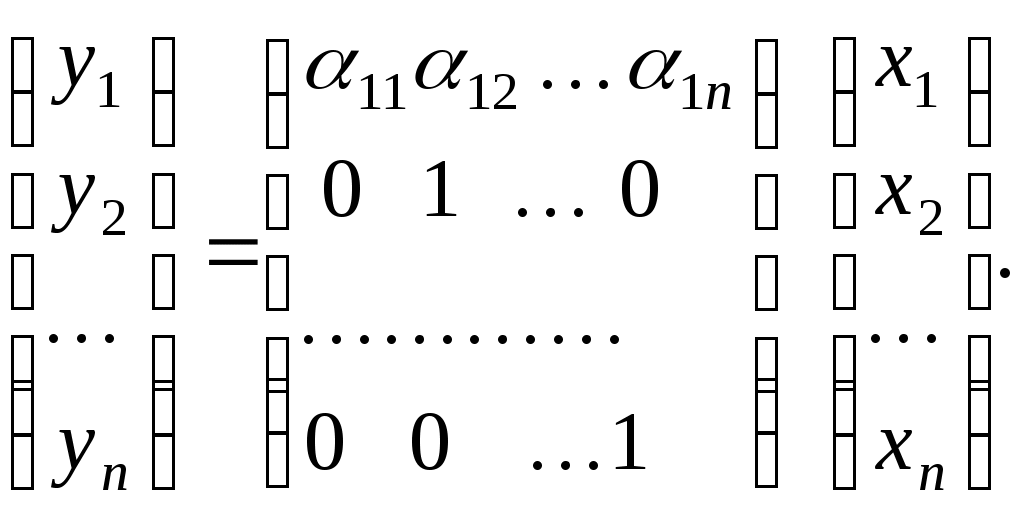
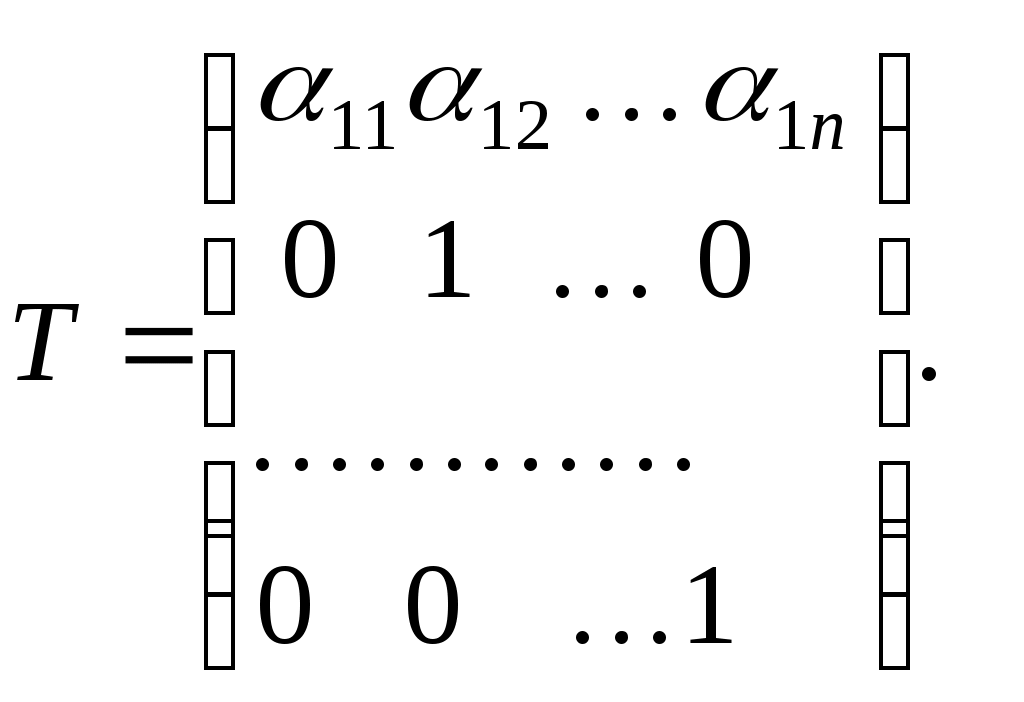
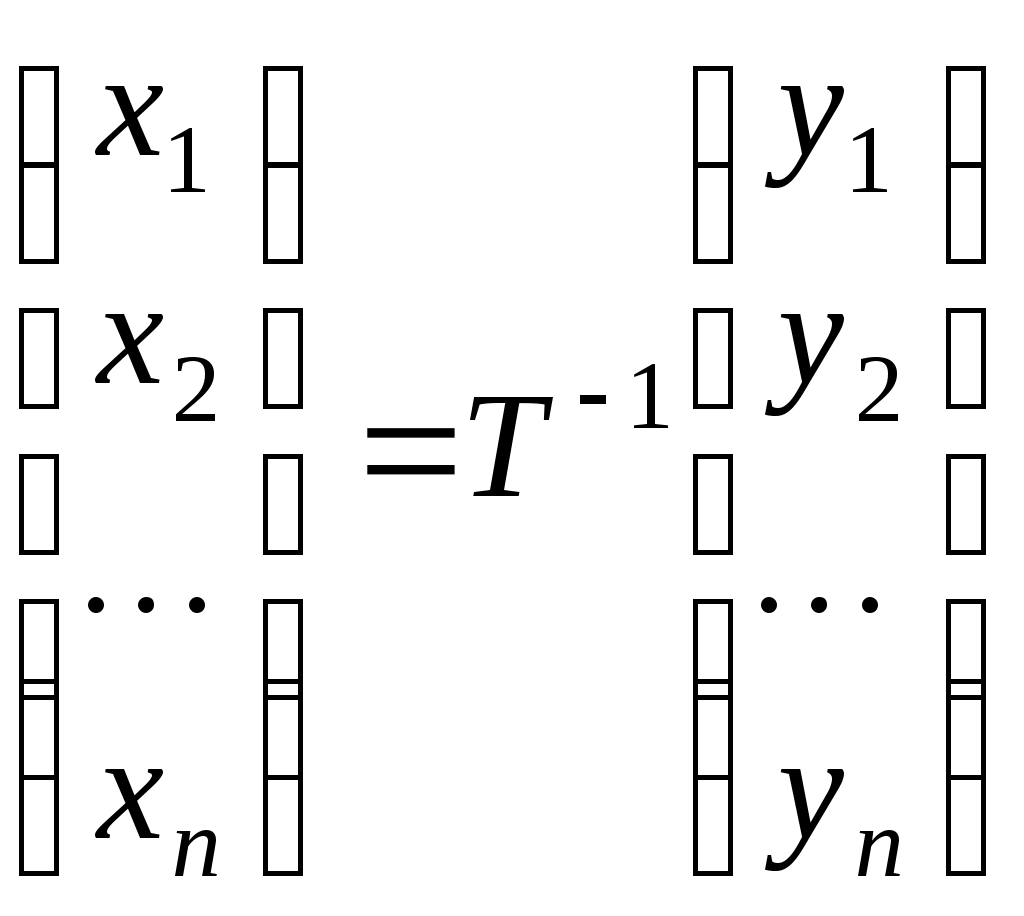 .
. .
.