|
|
Билинейные формы Шестаков. Білінійні та квадратичні функції С. С. Шестаков. Конспект лекцій для студентів заочного відділенння
Додатні квадратичні функції
Означення. Квадратична функція  на векторному просторі на векторному просторі  над полем над полем називається додатною, якщо для називається додатною, якщо для 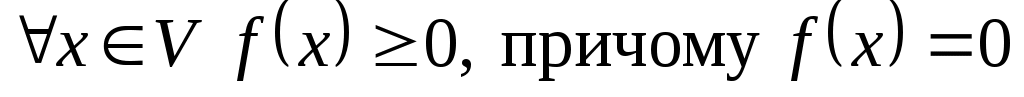 тоді і тільки тоді, коли тоді і тільки тоді, коли 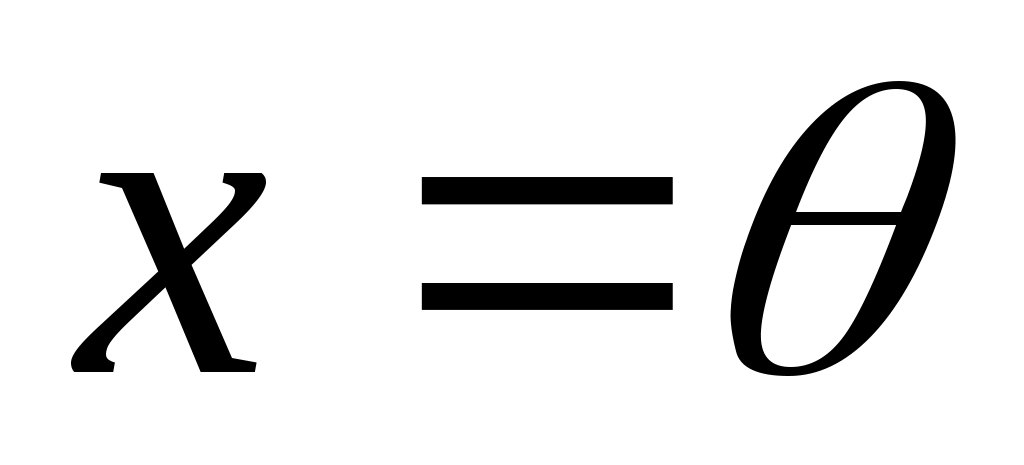 . .
Нехай  - полярна симетрична білінійна функція, що породжує додатну квадратичну функцію - полярна симетрична білінійна функція, що породжує додатну квадратичну функцію  , тоді , тоді  задає на просторі задає на просторі  скалярний добуток. скалярний добуток.
Дійсно, перевіримо виконання умов скалярного добутку:
1. 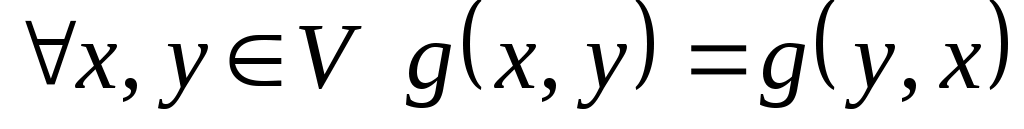 . .
Це випливає з симетричності білінійної функції 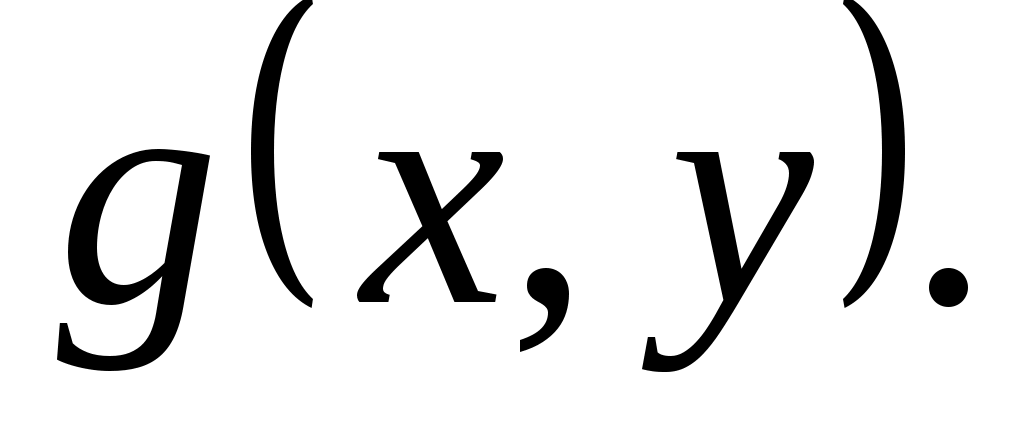
2. 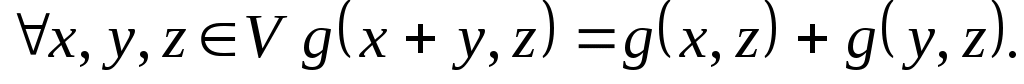
3. 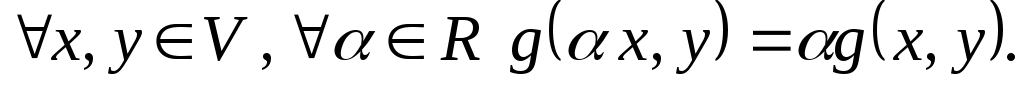
Виконання цих умов випливає з лінійності функції за першим аргументом. за першим аргументом.
4.  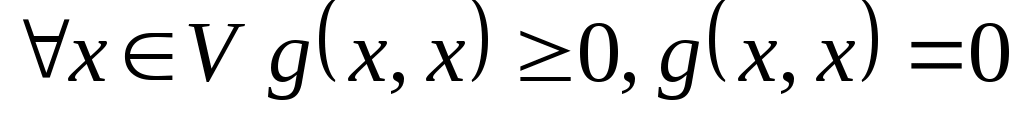 тоді і тільки тоді, коли тоді і тільки тоді, коли 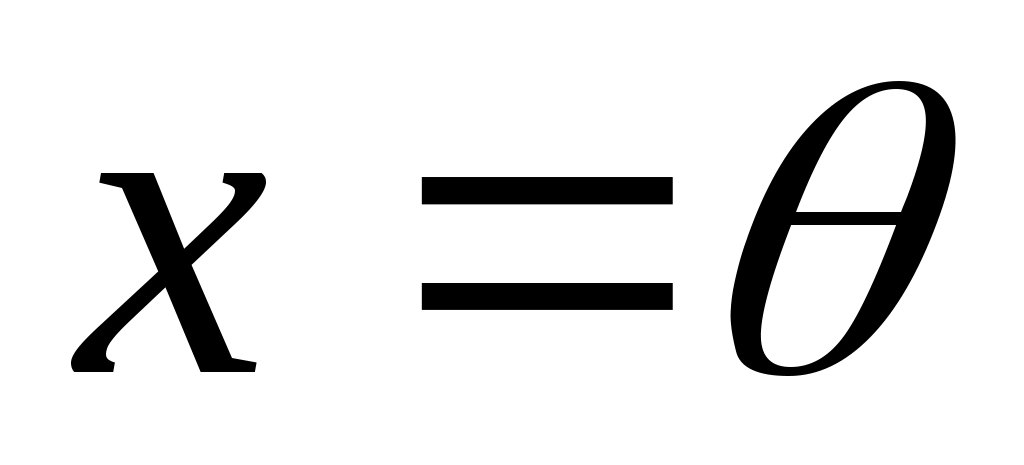 . .
Умова виконується, оскільки 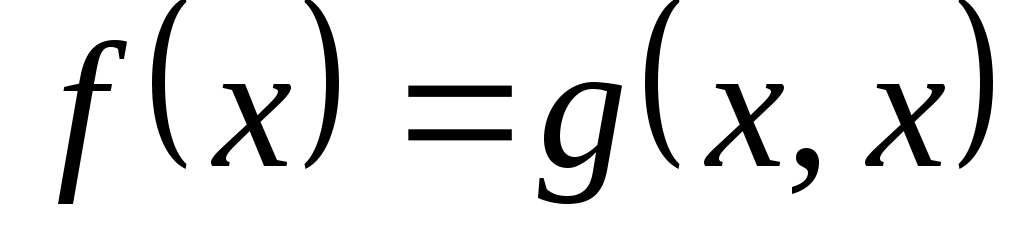 - додатна квадратична функція. - додатна квадратична функція.
Критерій Сильвестера
Будемо казати, що матриця  з дійсними елементами задовольняє умову Сильвестера, якщо всі її кутові мінори додатні. з дійсними елементами задовольняє умову Сильвестера, якщо всі її кутові мінори додатні.
Тобто, якщо  - порядок матриці, а - порядок матриці, а 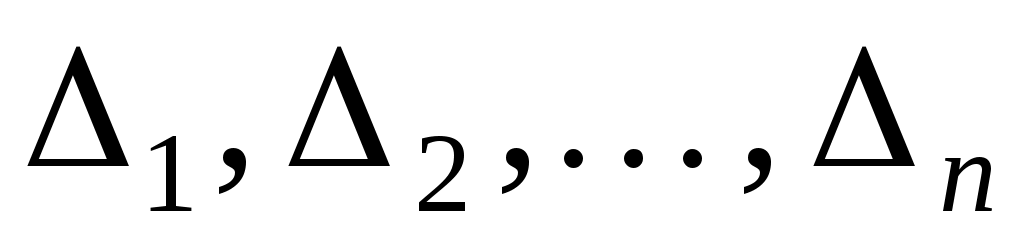 - всі кутові мінори матриці, то - всі кутові мінори матриці, то 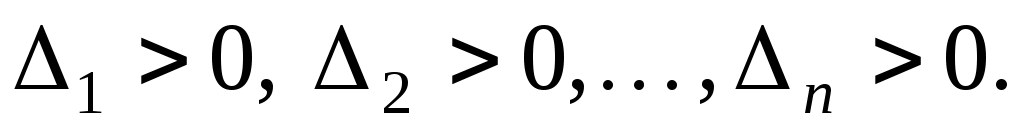
Теорема (критерій Сильвестера). Квадратична функція на скінченновимірному векторному просторі додатна тоді і тільки тоді, коли в деякому базисі простору її матриця задовольняє умову Сильвестера.
Доведення. Необхідність. Нехай  - додатна квадратична функція на скінченновимірному просторі - додатна квадратична функція на скінченновимірному просторі  . Покажемо, що в будь-якому базисі . Покажемо, що в будь-якому базисі  простору матриця квадратичної функції простору матриця квадратичної функції
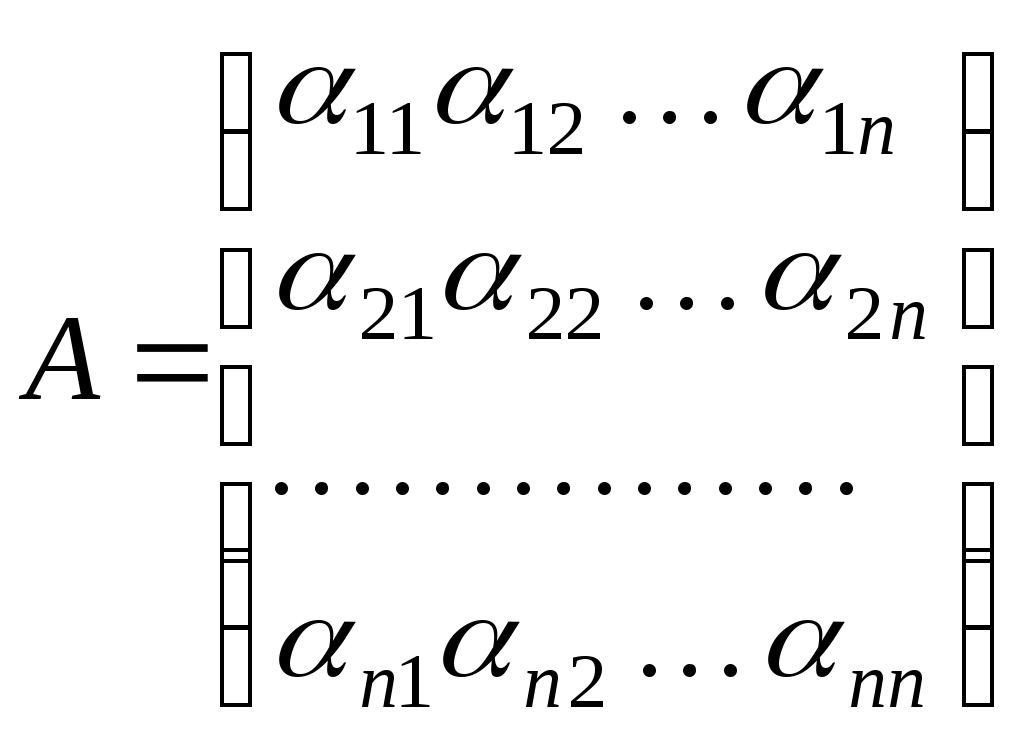
задовольняє умову Сильвестера.
Доведемо це індукцією за розмірністю  простору. простору.
Нехай спочатку 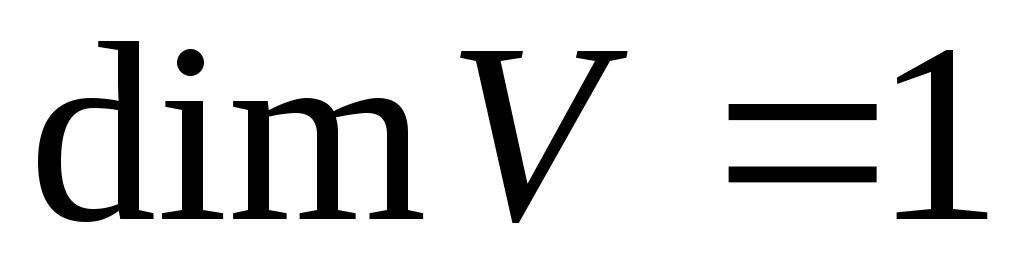 , ненульовий вектор , ненульовий вектор 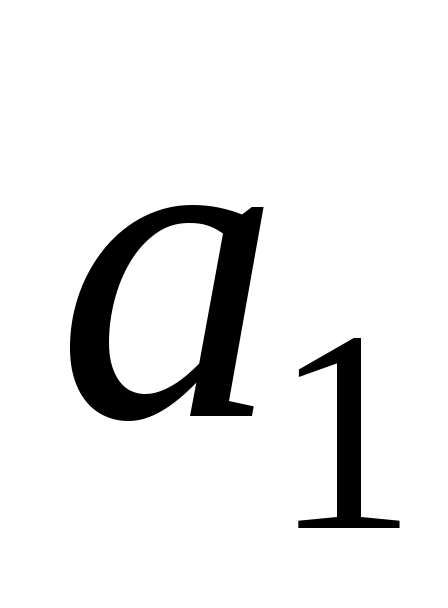 утворює базис утворює базис  . Тоді в цьому базисі квадратична функція . Тоді в цьому базисі квадратична функція  задається квадратичною формою: задається квадратичною формою:
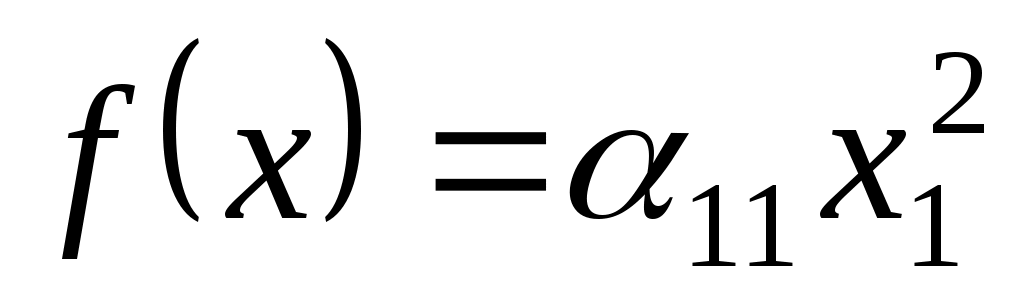 . .
Припустимо, що 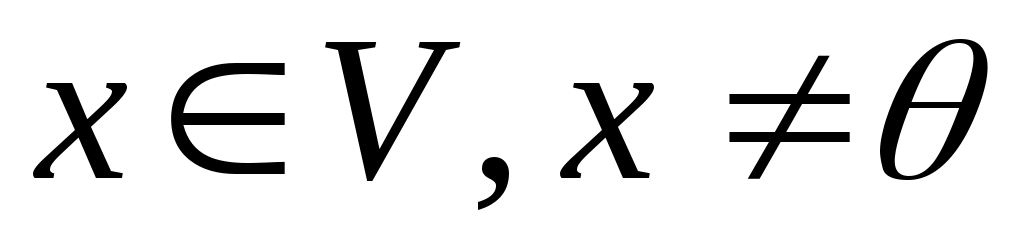 . Тоді . Тоді 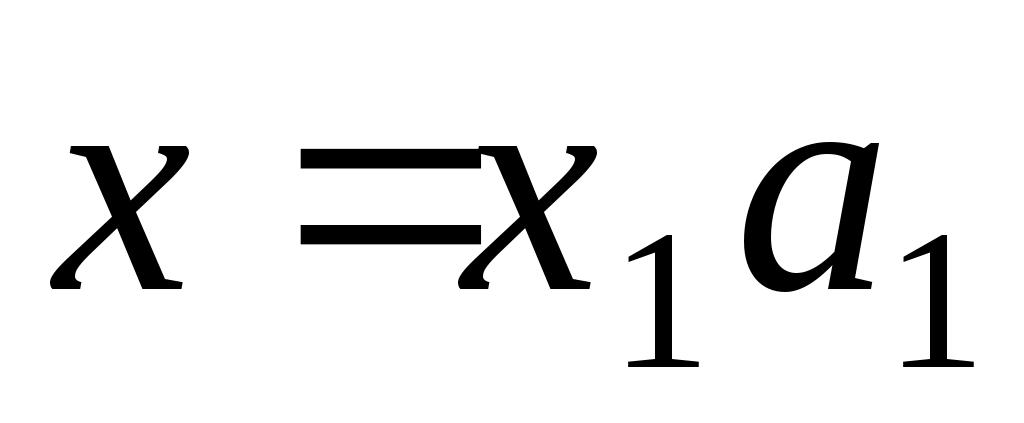 для деякого для деякого 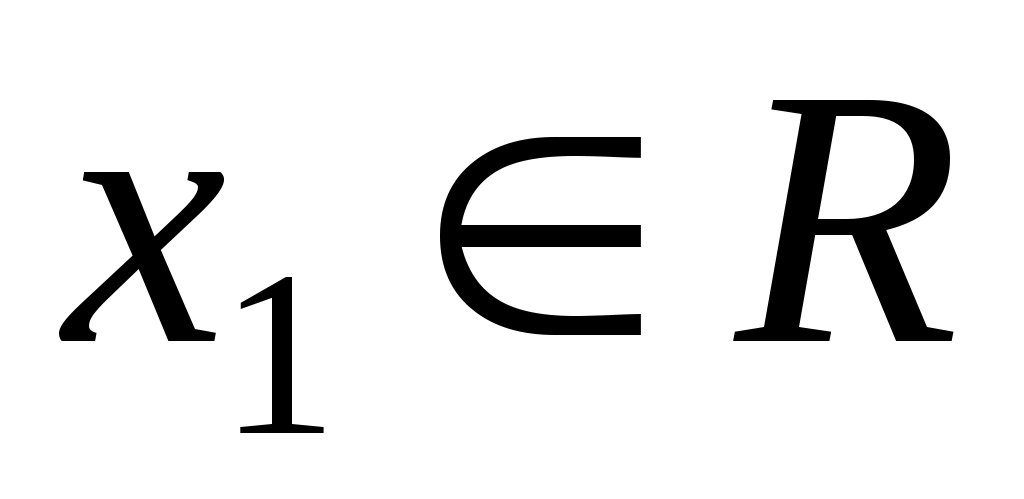 , причому , причому 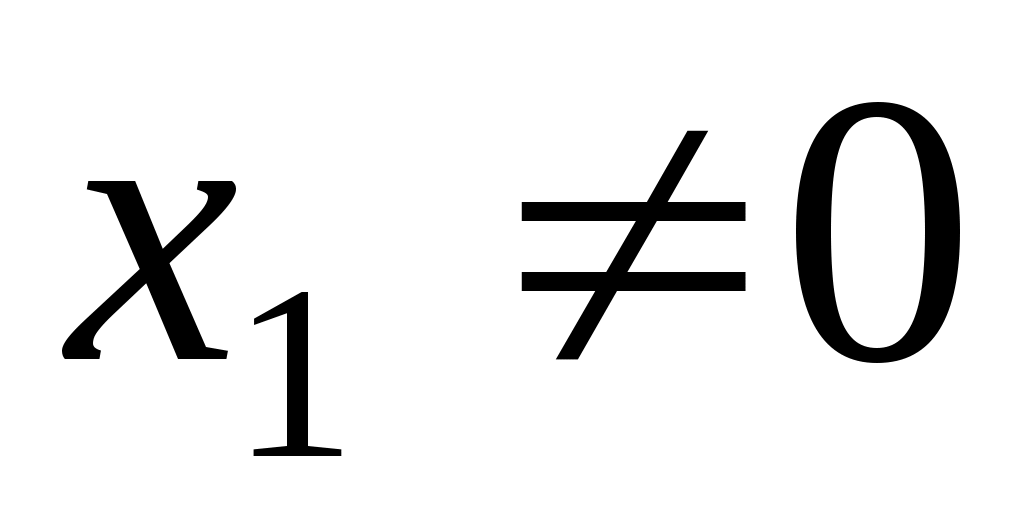 ; ; 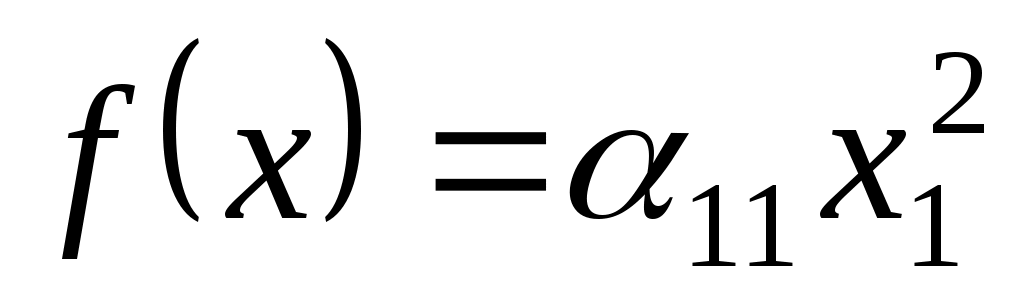 і, оскільки і, оскільки  - додатна квадратична функція, то - додатна квадратична функція, то 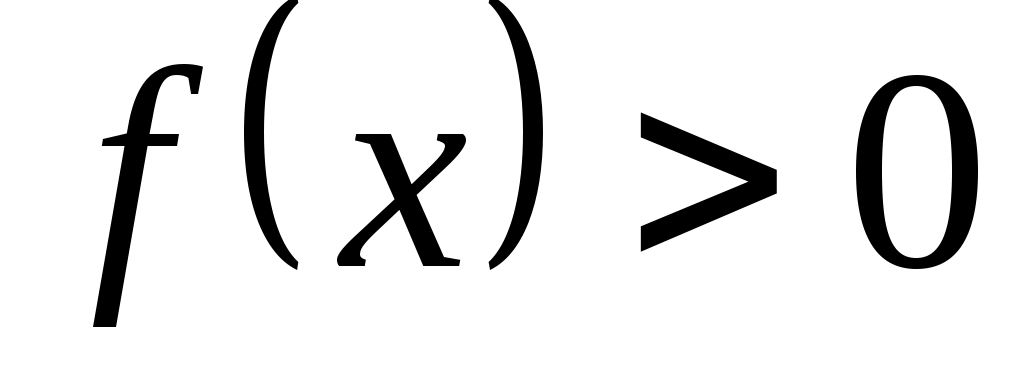 . Але . Але 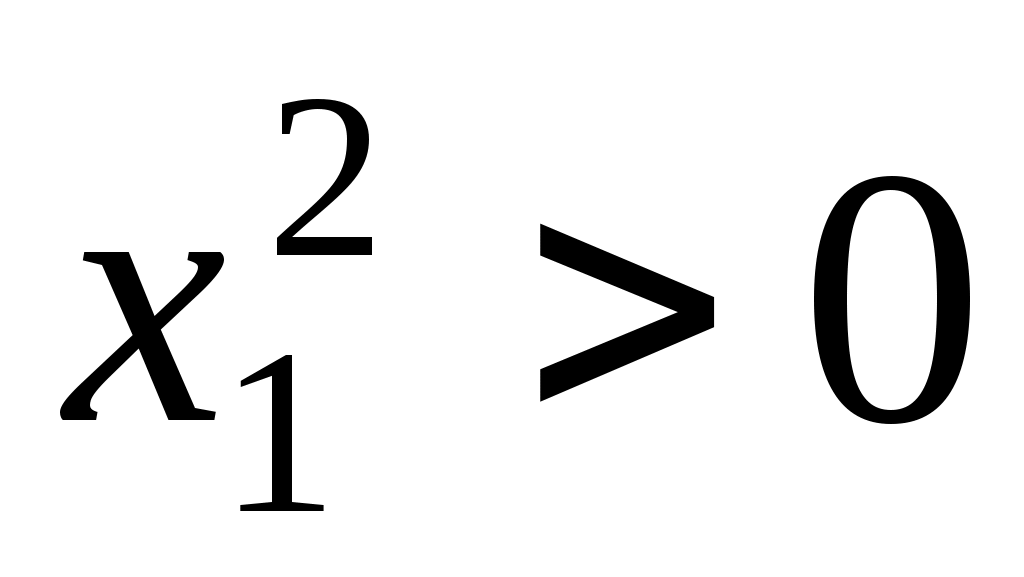 , тому , тому
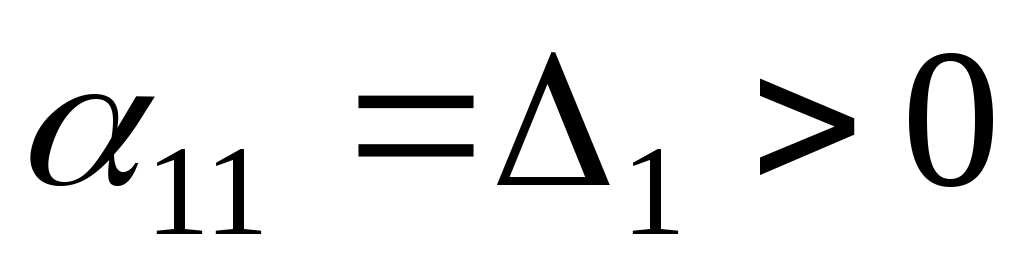 . .
Припустимо тепер, що твердження виконується для всіх просторів розмірності менше  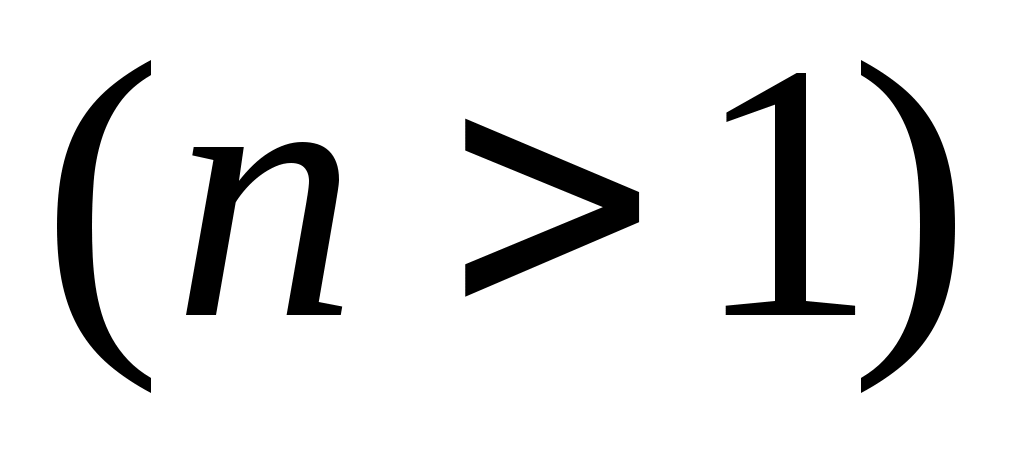 , тобто, будь-яка квадратична функція в будь-якому базисі такого простору задається матрицею, яка задовольняє умову Сильвестера. І нехай , тобто, будь-яка квадратична функція в будь-якому базисі такого простору задається матрицею, яка задовольняє умову Сильвестера. І нехай 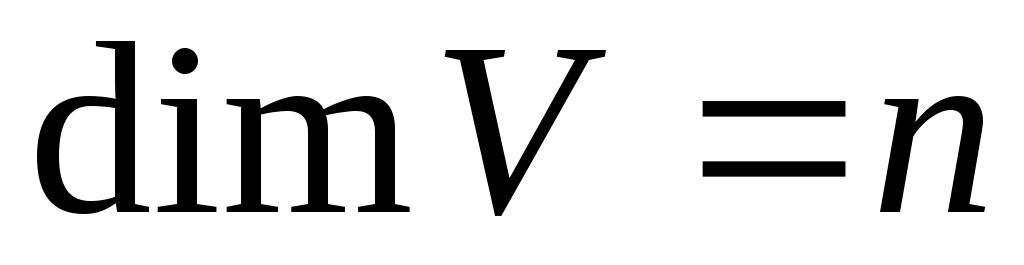 , ,  - деяка квадратична функція на - деяка квадратична функція на  , ,  - фіксований базис простору, в якому функції - фіксований базис простору, в якому функції  відповідає матриця відповідає матриця
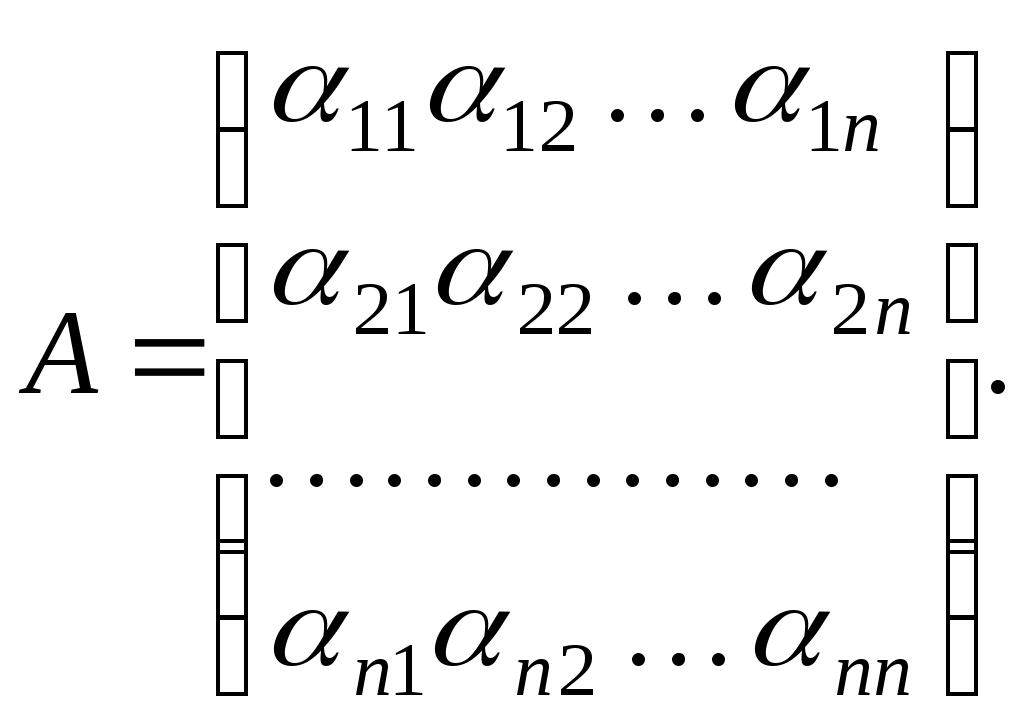
Покажемо, що 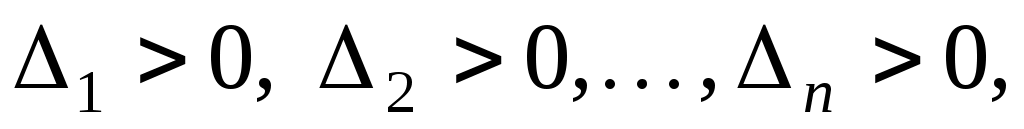 де де 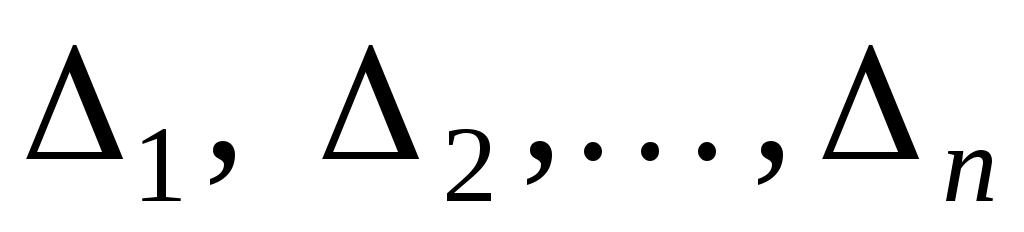 - всі кутові мінори матриці - всі кутові мінори матриці  . У цьому базисі квадратична функція задається такою квадратичною формою: . У цьому базисі квадратична функція задається такою квадратичною формою:
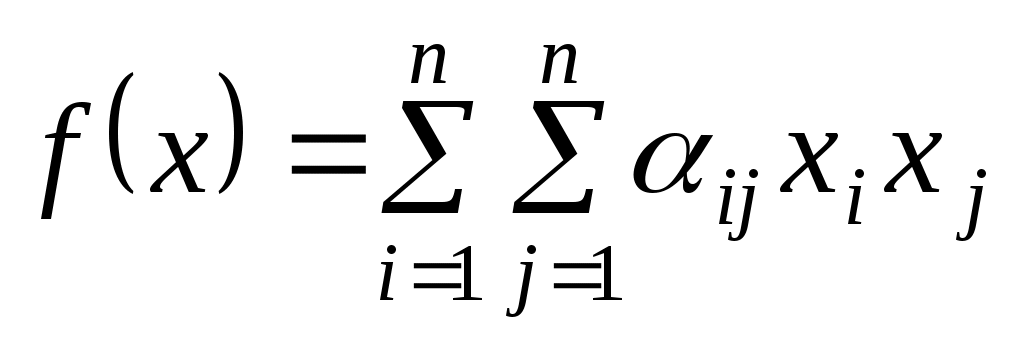 . .
Цю квадратичну форму можна переписати так:
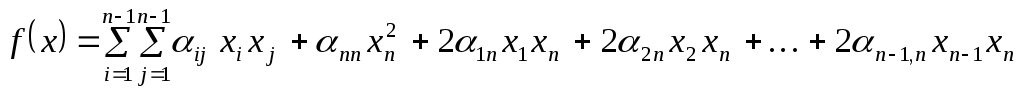 . .
Визначимо підпростір 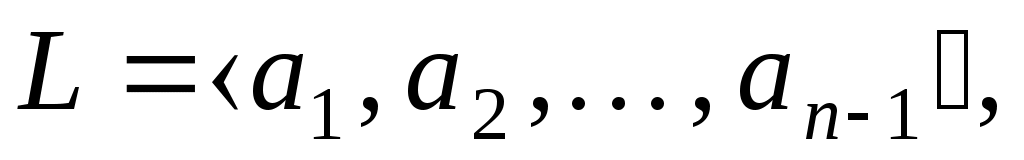 і нехай і нехай
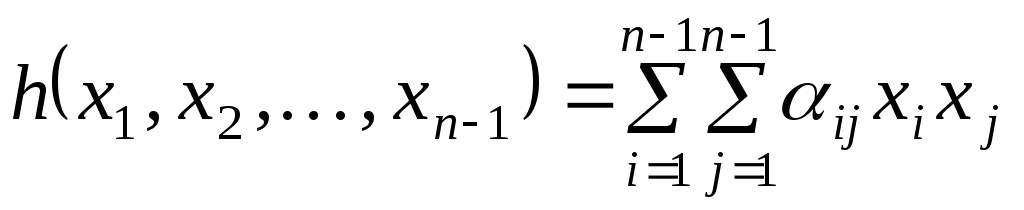 . .
Тоді 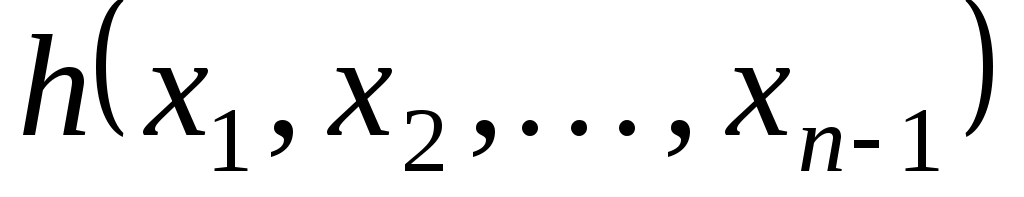 - квадратична форма від змінних - квадратична форма від змінних 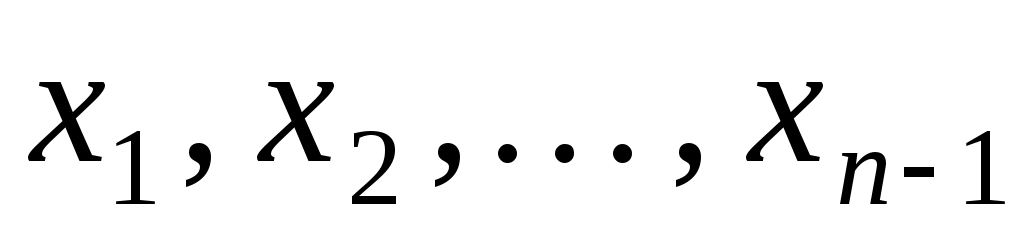 , яка при фіксованому базисі , яка при фіксованому базисі 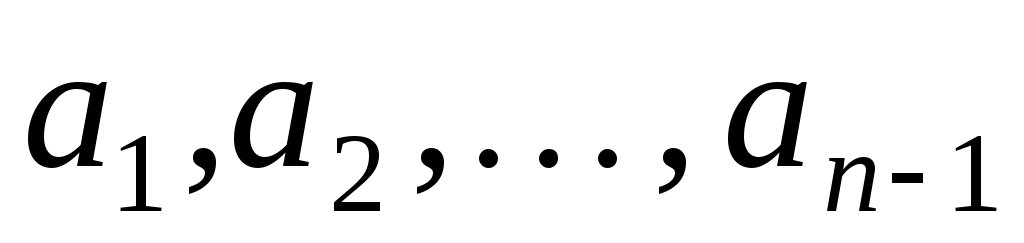 підпростору підпростору 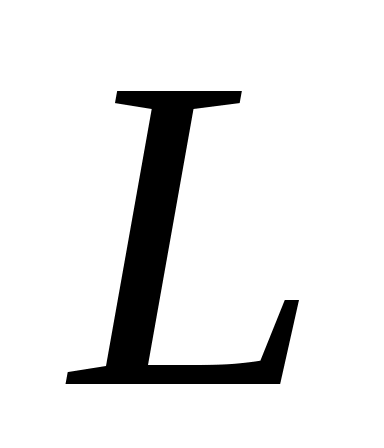 задає на цьому підпросторі деяку квадратичну функцію задає на цьому підпросторі деяку квадратичну функцію 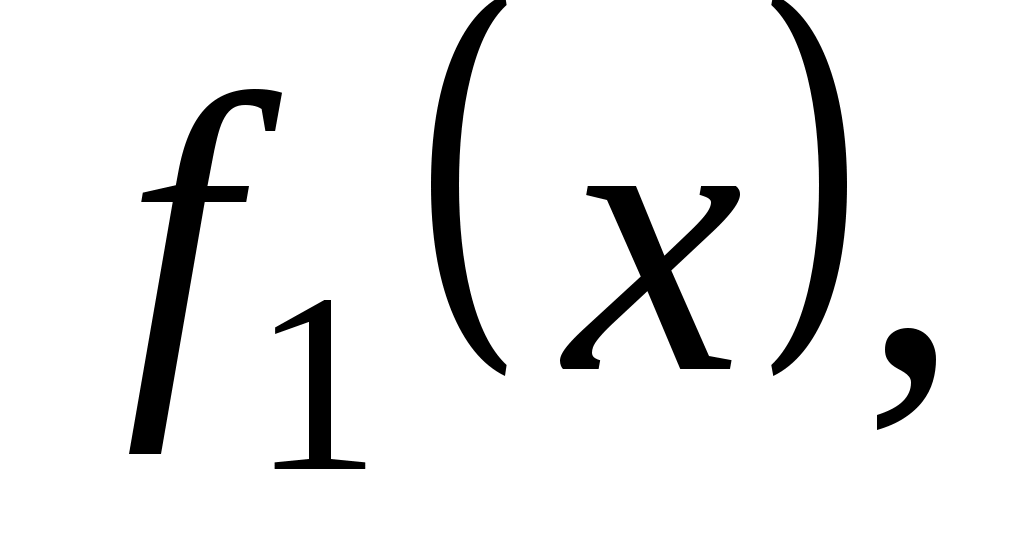 причому причому 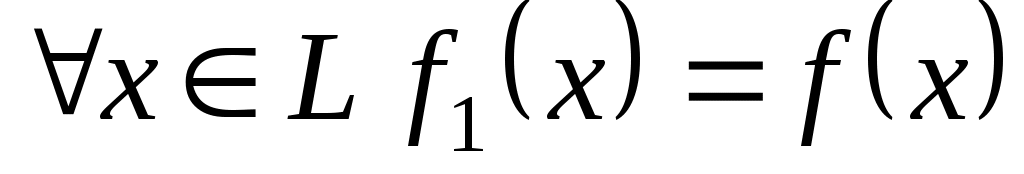 . Тому, оскільки функція . Тому, оскільки функція 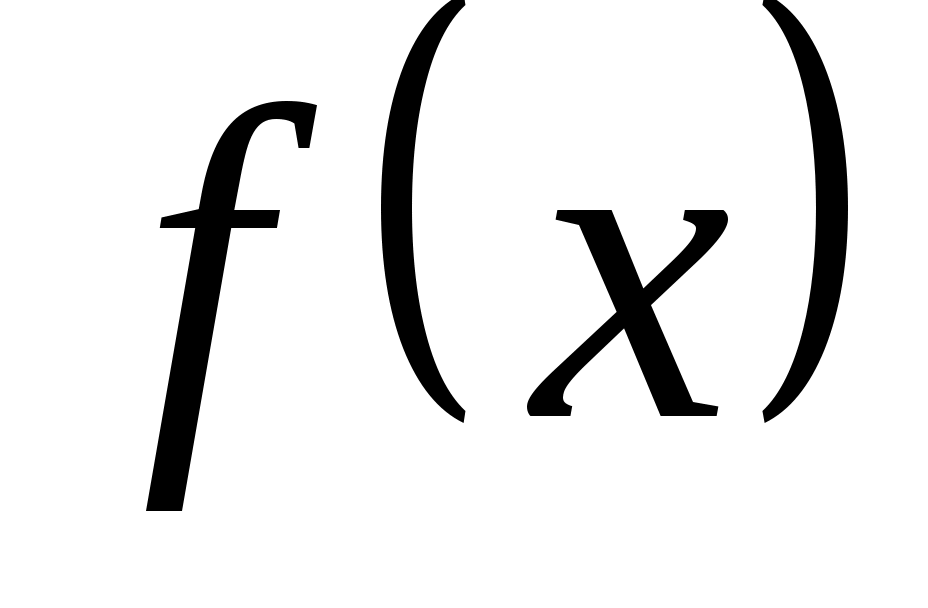 додатна, то і функція додатна, то і функція 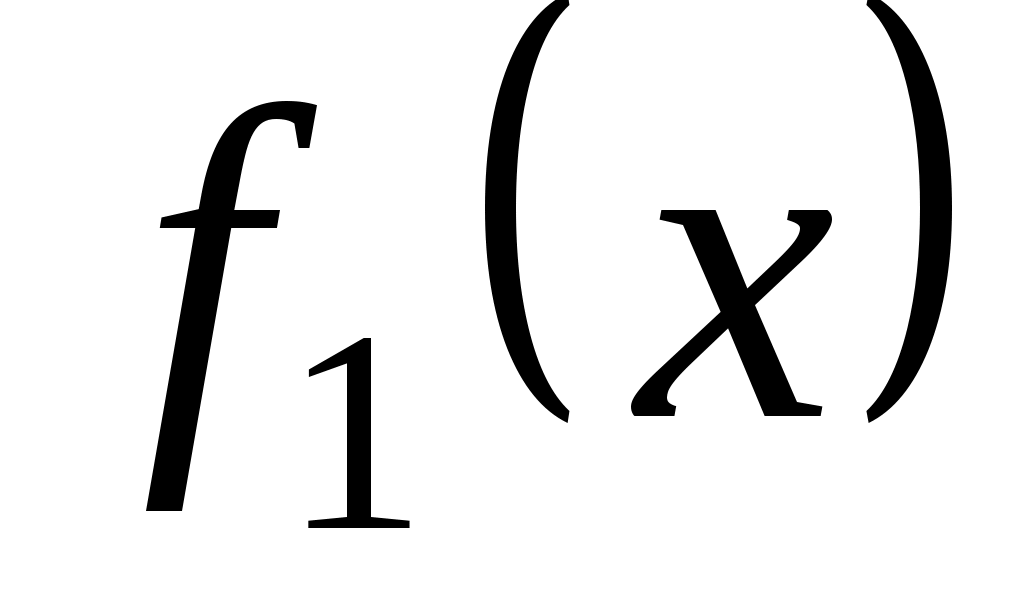 додатна. Але додатна. Але
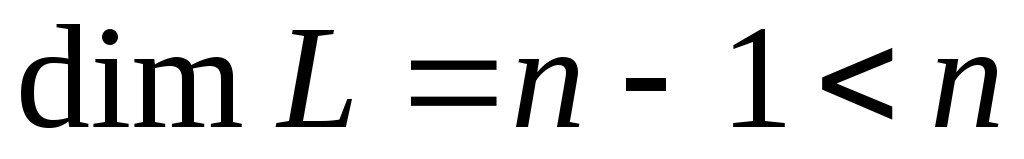 , ,
тому, за припущенням індукції, матриця квадратичної функції 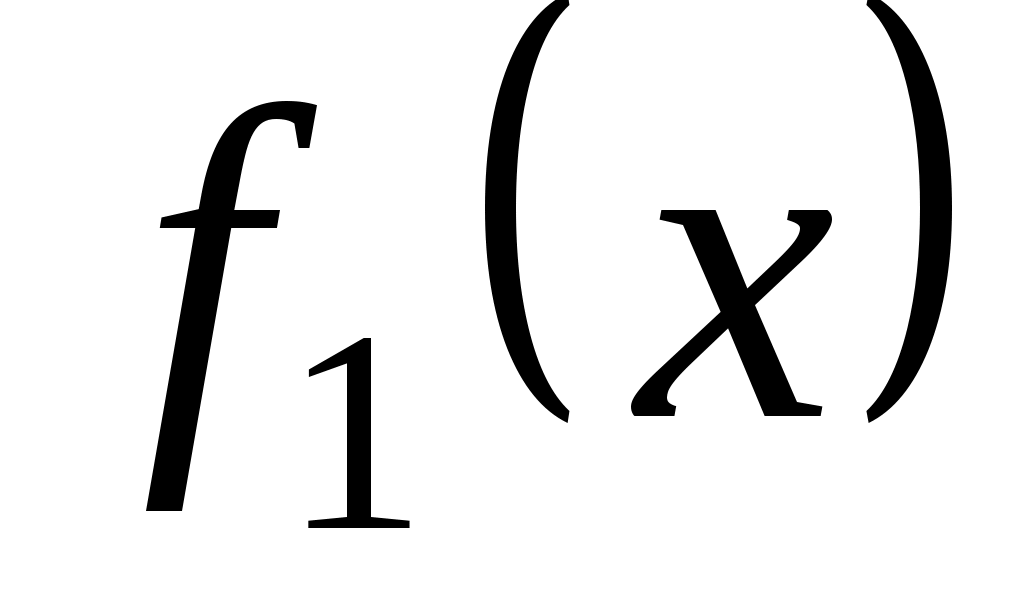 на підпросторі на підпросторі 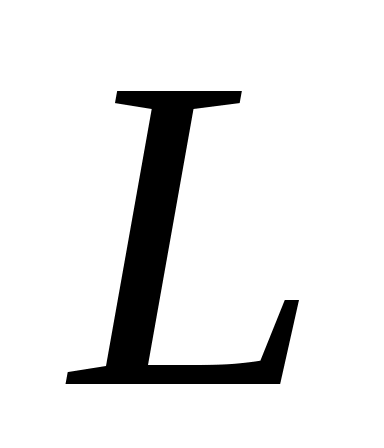 у базисі у базисі 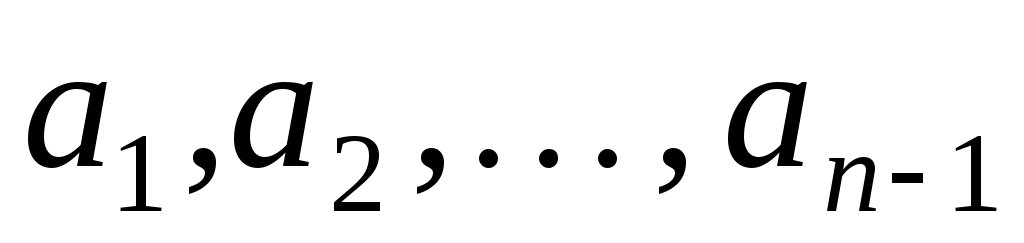 задовольняє умову Сильвестера. Ця матриця співпадає з матрицею кутового мінору задовольняє умову Сильвестера. Ця матриця співпадає з матрицею кутового мінору 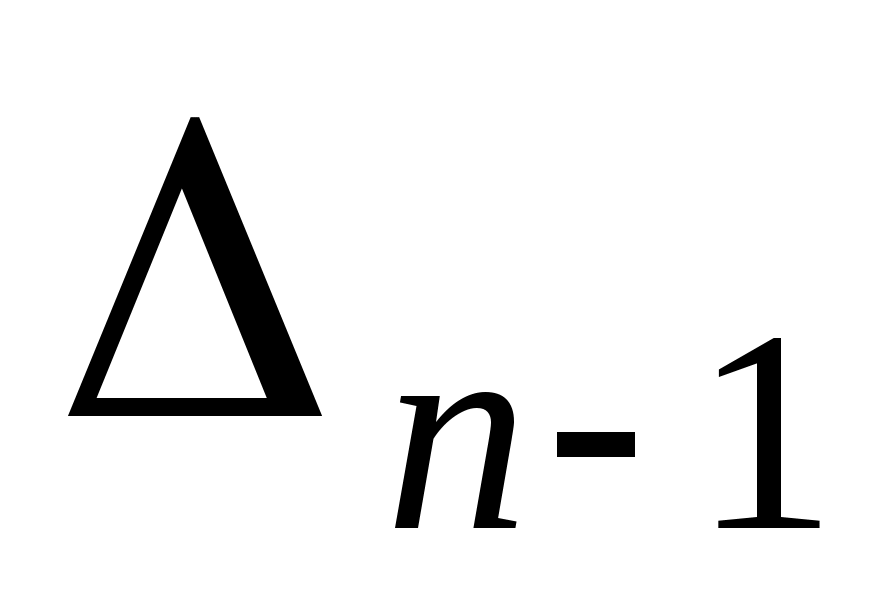 матриці матриці 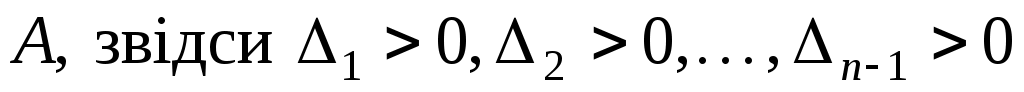 . .
Залишається показати, що 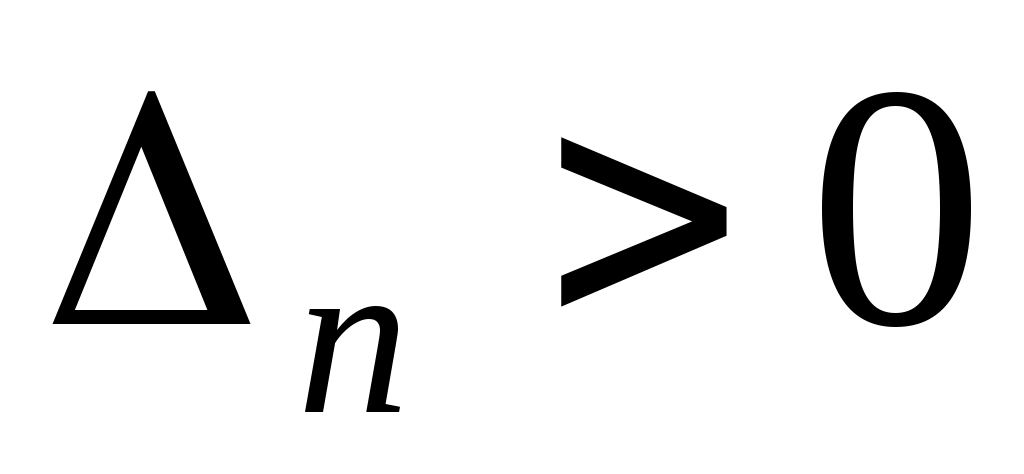 . Зводимо квадратичну функцію . Зводимо квадратичну функцію  до канонічного вигляду. При цьому знаходимо базис простору до канонічного вигляду. При цьому знаходимо базис простору  , у якому функції , у якому функції  відповідає діагональна матриця: відповідає діагональна матриця:
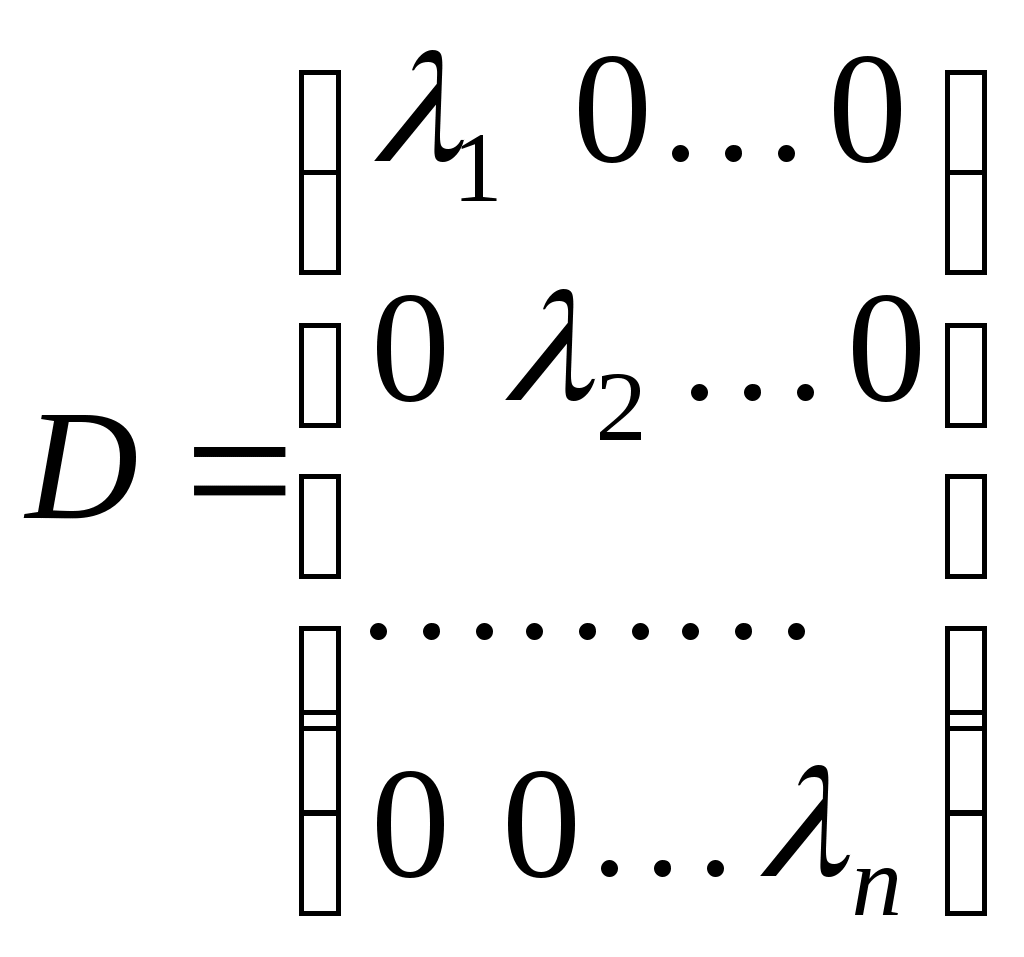 . .
Зрозуміло, що
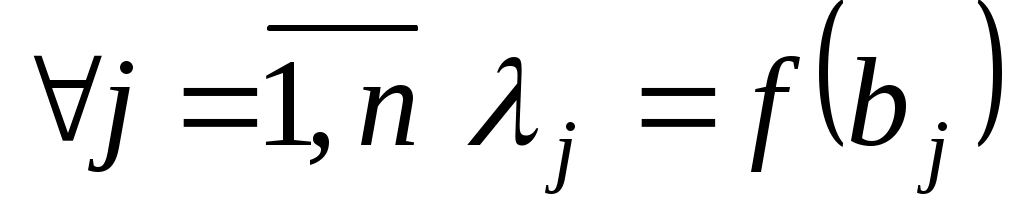 , ,
і, оскільки
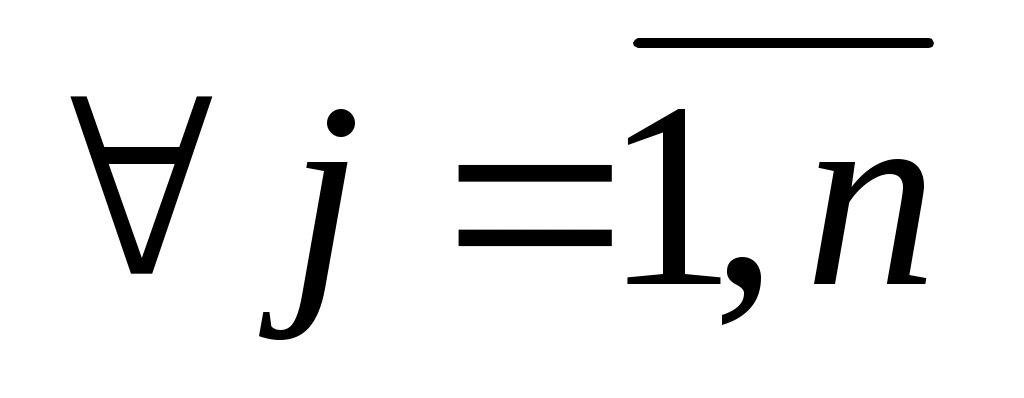 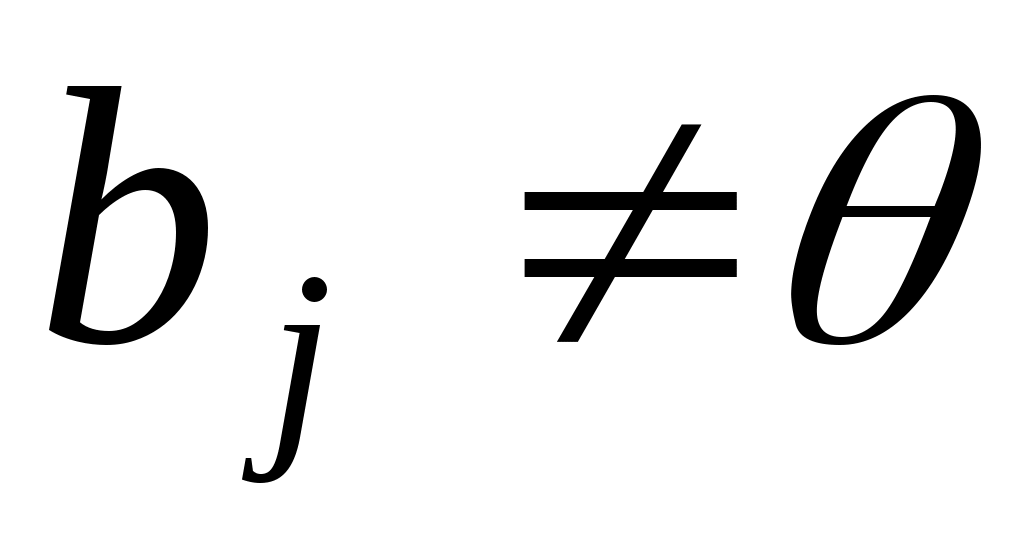 , ,
то
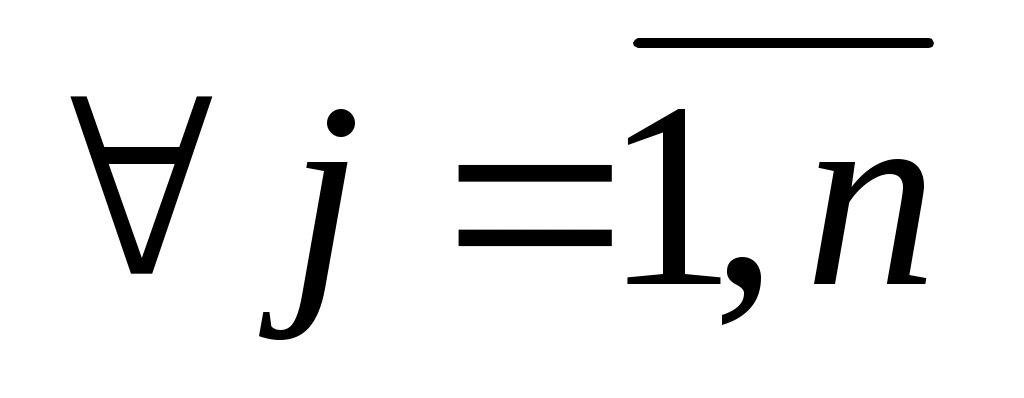 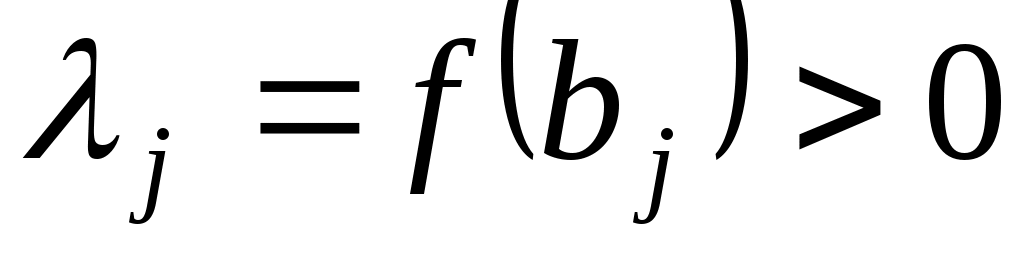 . .
Якщо  - матриця переходу від базису - матриця переходу від базису 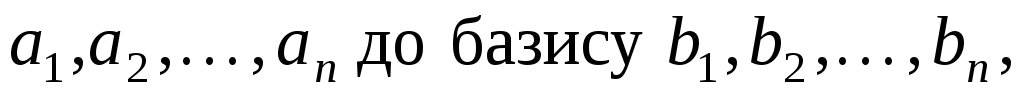 то то
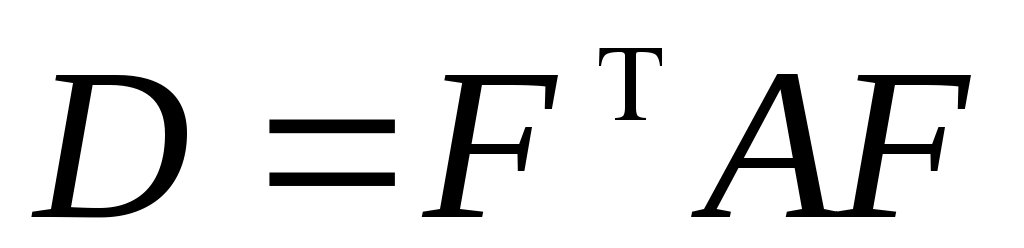 , ,
причому 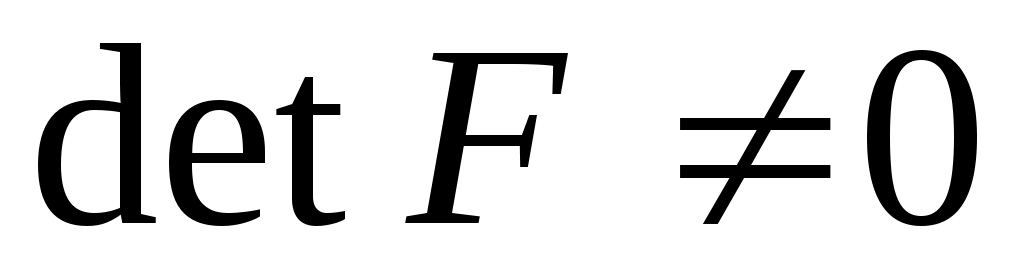 . Тоді . Тоді
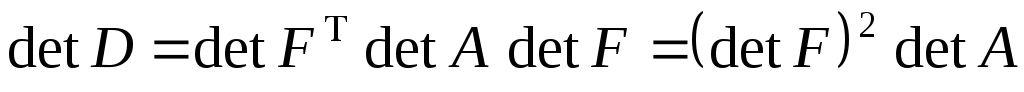 , ,
і, оскільки
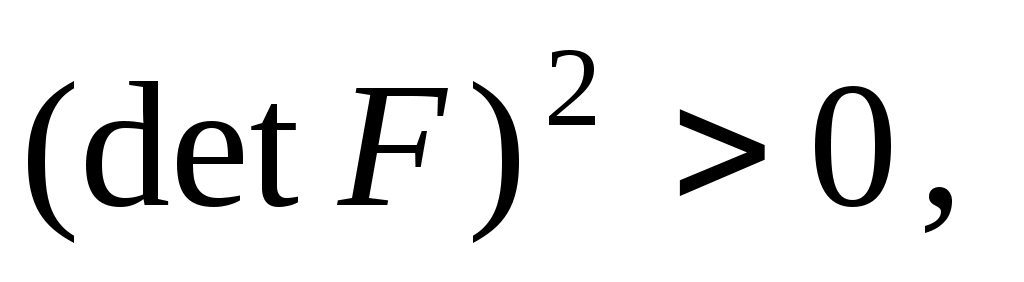
а
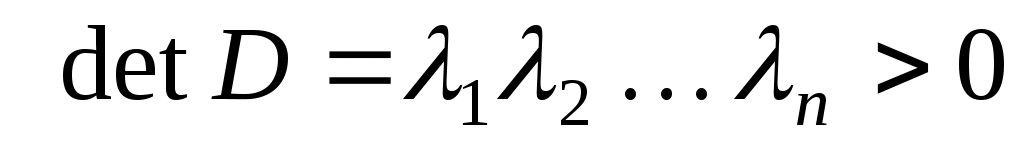 , ,
то
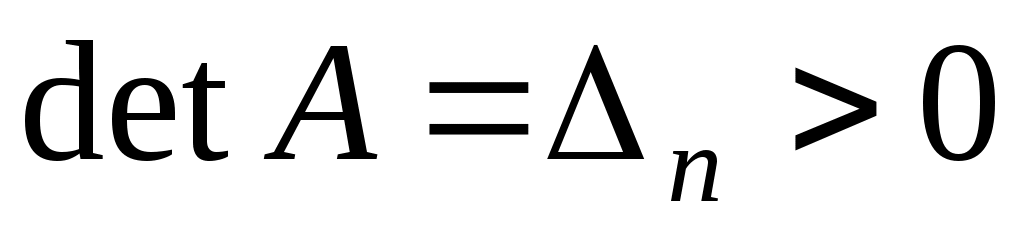 . .
Достатність. Припустимо, що  - квадратична функція на скінченновимірному векторному просторі - квадратична функція на скінченновимірному векторному просторі  , і в базисі , і в базисі  простору її матриця простору її матриця  задовольняє умову Сильвестера. Тоді ця матриця задовольняє і умову Якобі, а тому існує базис задовольняє умову Сильвестера. Тоді ця матриця задовольняє і умову Якобі, а тому існує базис  простору, в якому функція простору, в якому функція  задається канонічною квадратичною формою: задається канонічною квадратичною формою:
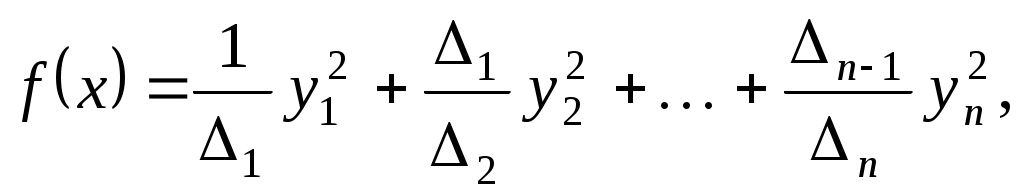
де 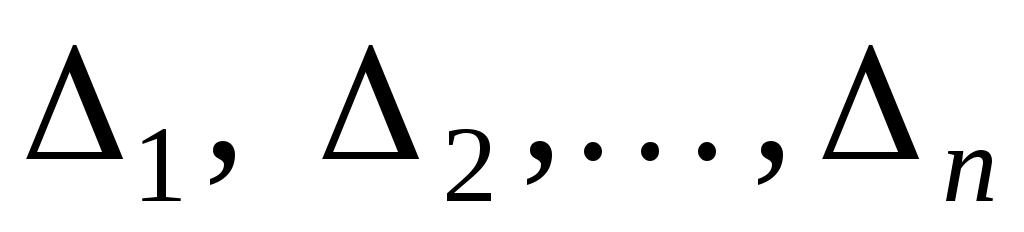 - всі кутові мінори матриці - всі кутові мінори матриці  . За умовою теореми, всі коефіцієнти цієї квадратичної форми додатні. Припустимо, що . За умовою теореми, всі коефіцієнти цієї квадратичної форми додатні. Припустимо, що  -довільний вектор, який у базисі -довільний вектор, який у базисі  задається такими координатами: задається такими координатами: 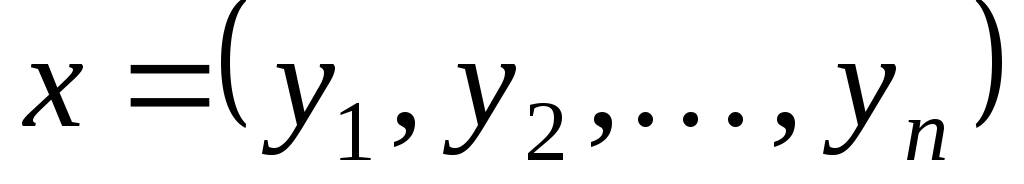 . Тоді . Тоді
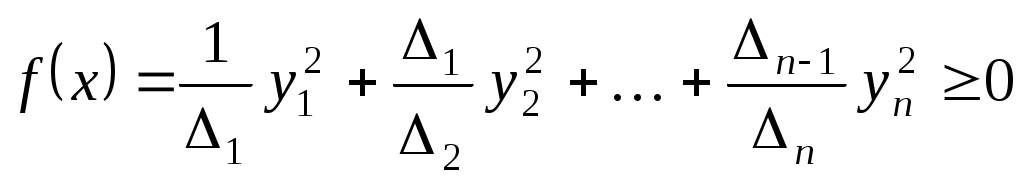 . .
Якщо 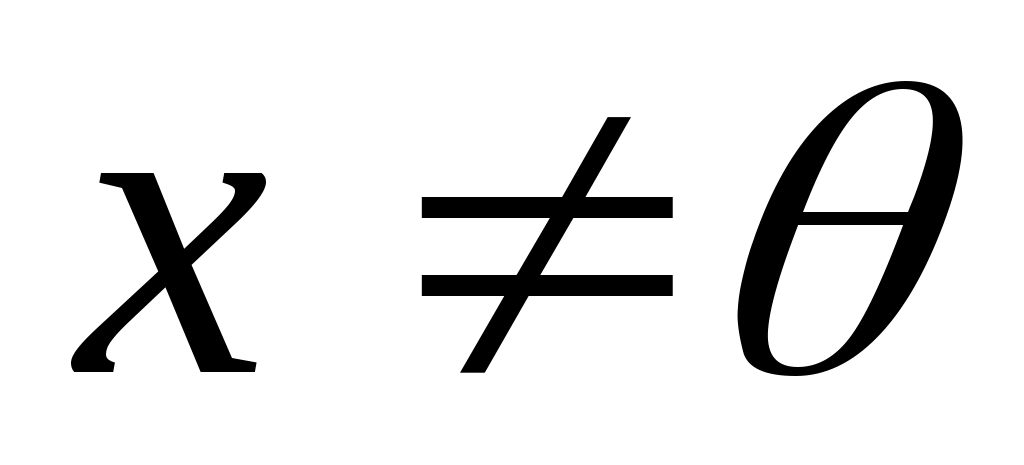 , то серед координат , то серед координат 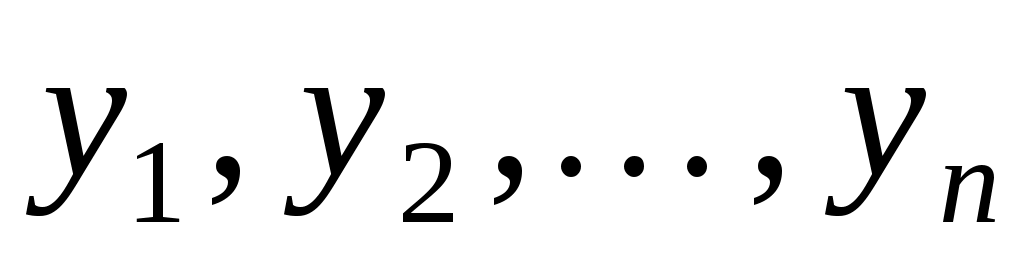 є ненульові, а тому є ненульові, а тому 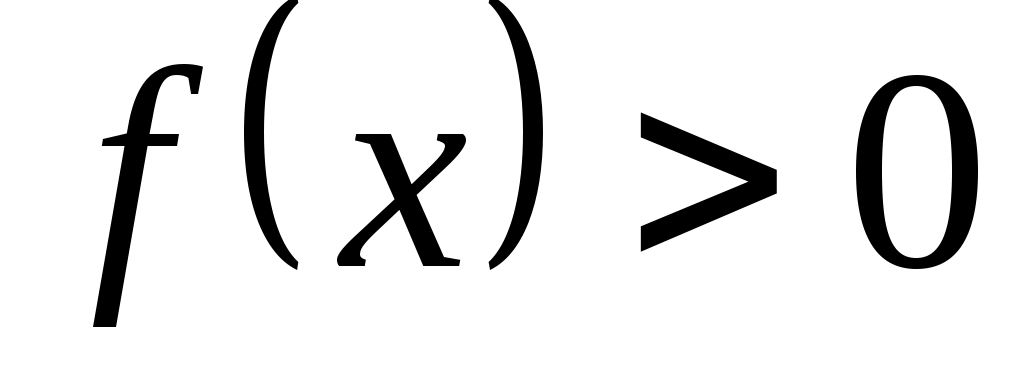 , тобто, функція , тобто, функція  додатна. додатна.
Зауваження. В процесі доведення останньої теореми фактично було показано, що матриця додатної квадратичної функції на скінченновимірному просторі в будь-якому базисі задовольняє умову Сильвестера.
Застосування теорії симетричних матриць до теорії квадратичних функцій
Нехай  - симетрична матриця з дійсними елементами порядку - симетрична матриця з дійсними елементами порядку  . За теоремою про будову симетричної матриці існують діагональна матриця . За теоремою про будову симетричної матриці існують діагональна матриця 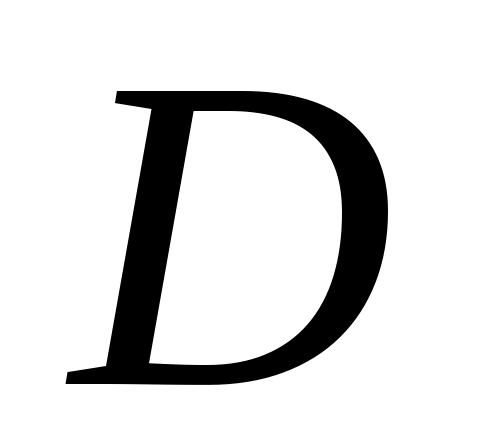 та ортогональна матриця та ортогональна матриця  , такі, що , такі, що 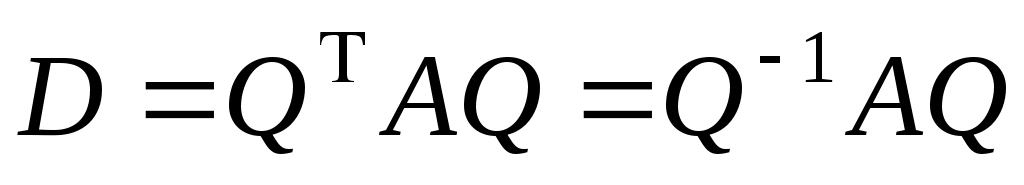 . Причому, якщо . Причому, якщо
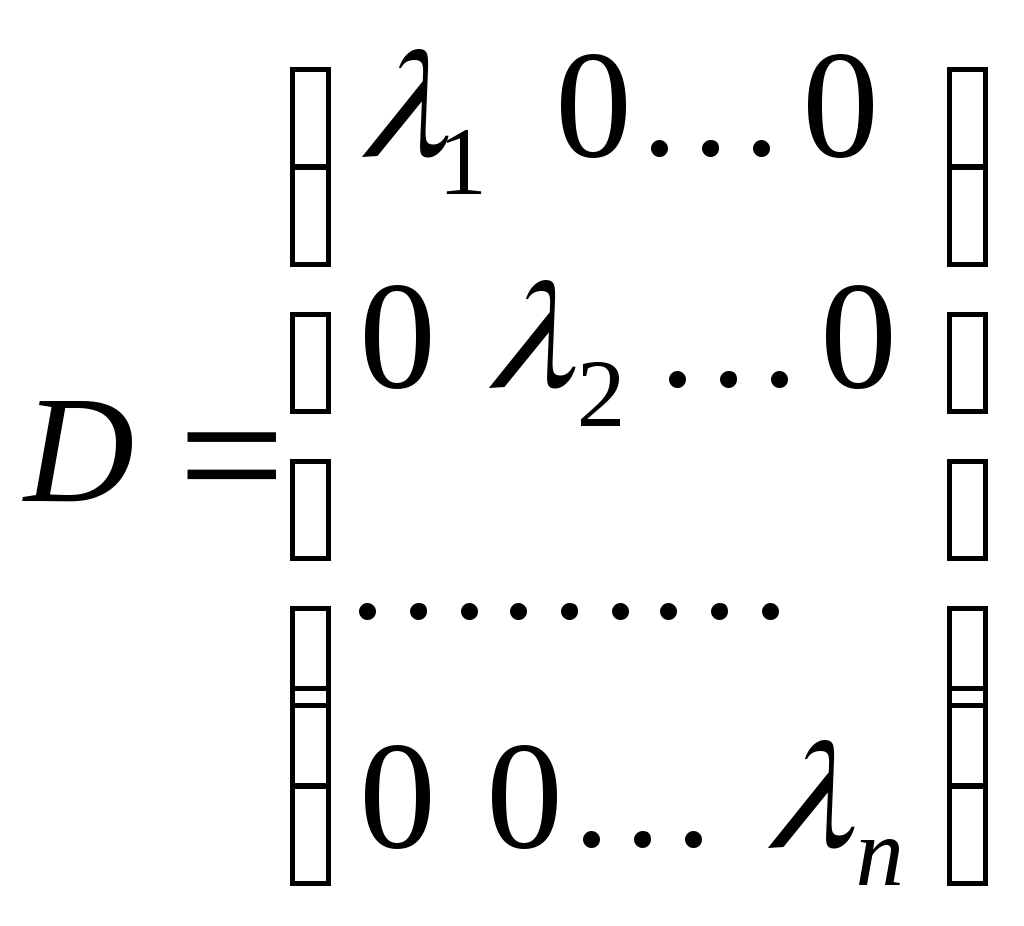 , ,
то 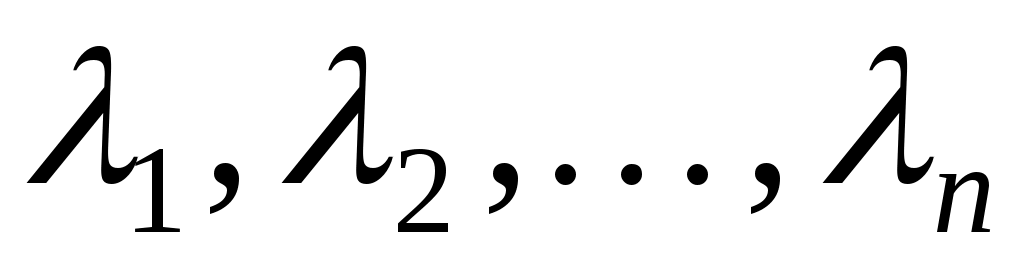 - усі власні числа матриці - усі власні числа матриці  , з урахуванням їх кратностей. Нехай тепер , з урахуванням їх кратностей. Нехай тепер  - векторний простір розмірності - векторний простір розмірності  над полем над полем  , ,  - деякий фіксований базис простору, - деякий фіксований базис простору,  - квадратична функція на просторі - квадратична функція на просторі  , якій у базисі , якій у базисі  відповідає матриця відповідає матриця . Припустимо також, що . Припустимо також, що  - такий базис простору - такий базис простору  , що матриця , що матриця 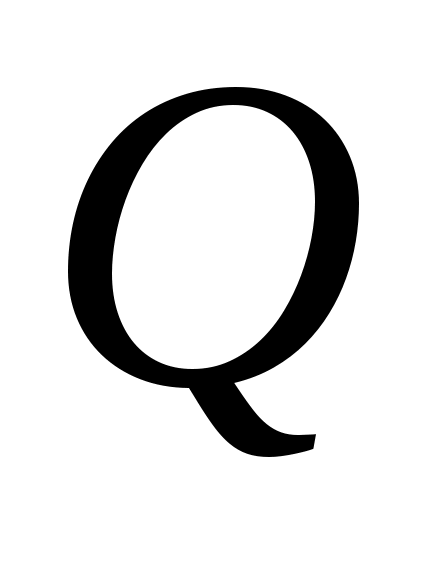 є матрицею переходу від базису є матрицею переходу від базису  до базису до базису  . У просторі . У просторі  можна ввести скалярний добуток, відповідний базису можна ввести скалярний добуток, відповідний базису  , таким чином. Для векторів , таким чином. Для векторів  , які в базисі , які в базисі  задаються такими координатами: задаються такими координатами:  , покладемо , покладемо
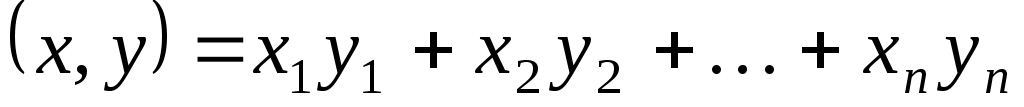 . .
Тоді при такому скалярному добутку базис  ортонормований і, оскільки матриця переходу ортонормований і, оскільки матриця переходу 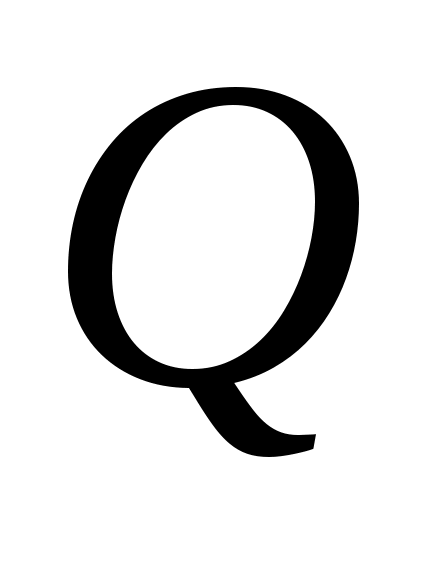 від базису від базису  до базису до базису  ортогональна, то базис ортогональна, то базис  також ортонормований. У цьому базисі квадратичній функції також ортонормований. У цьому базисі квадратичній функції  відповідає така матриця: відповідає така матриця:
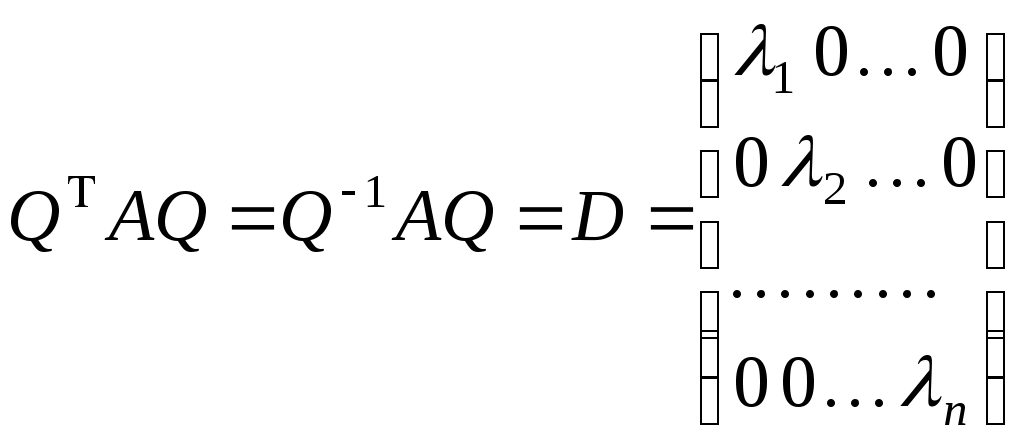 . .
Це означає, що в цьому базисі квадратична функція задається канонічною квадратичною формою:
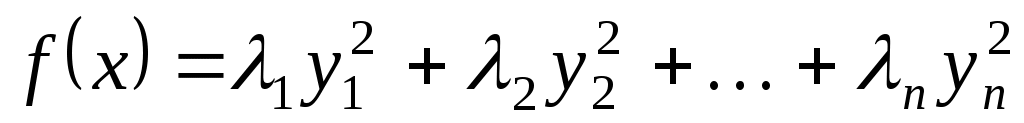 , ,
де 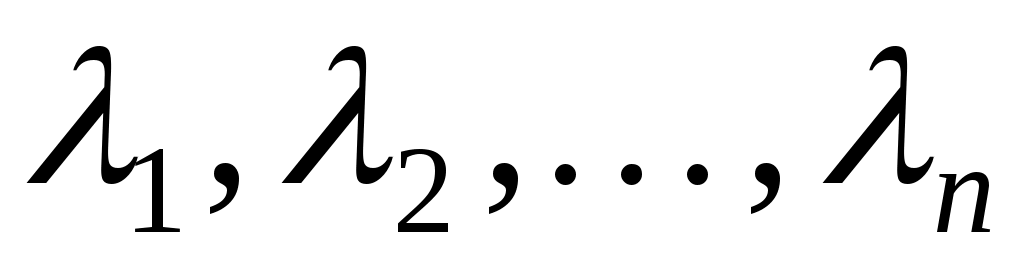 - усі власні числа матриці - усі власні числа матриці  . .
|
|
|
 Скачать 1.43 Mb.
Скачать 1.43 Mb.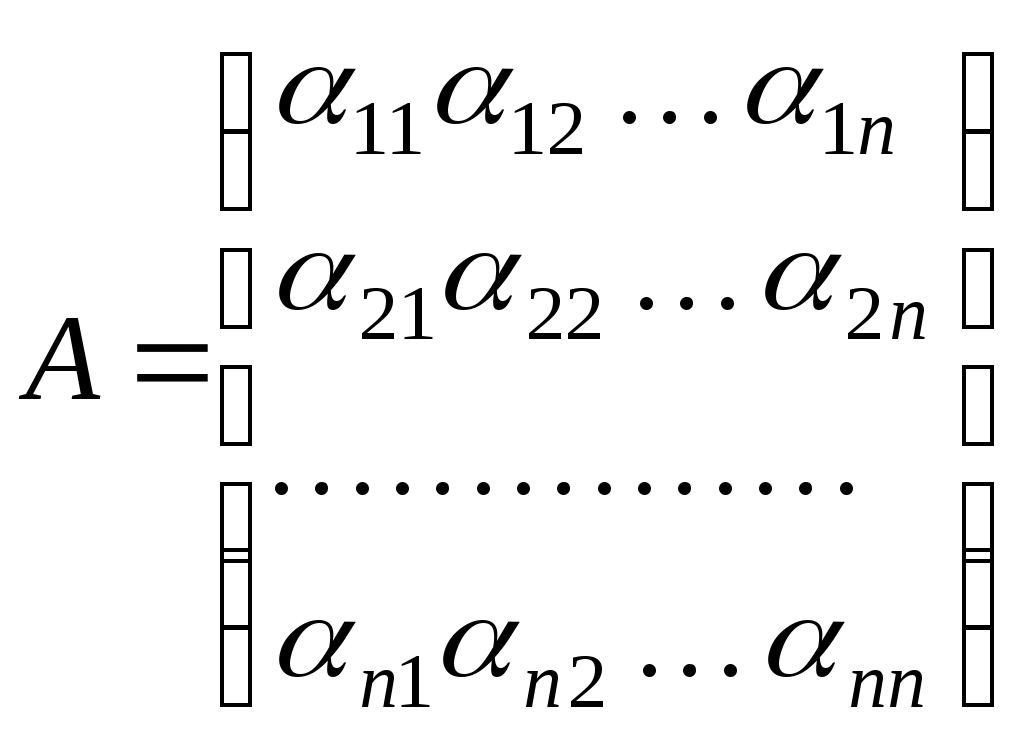
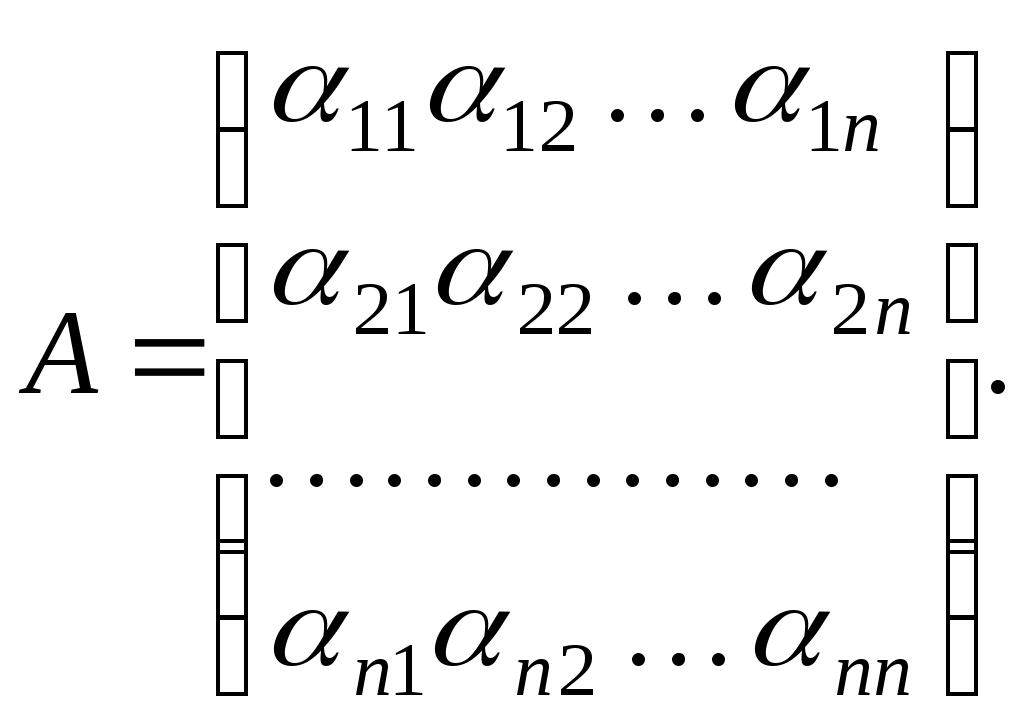
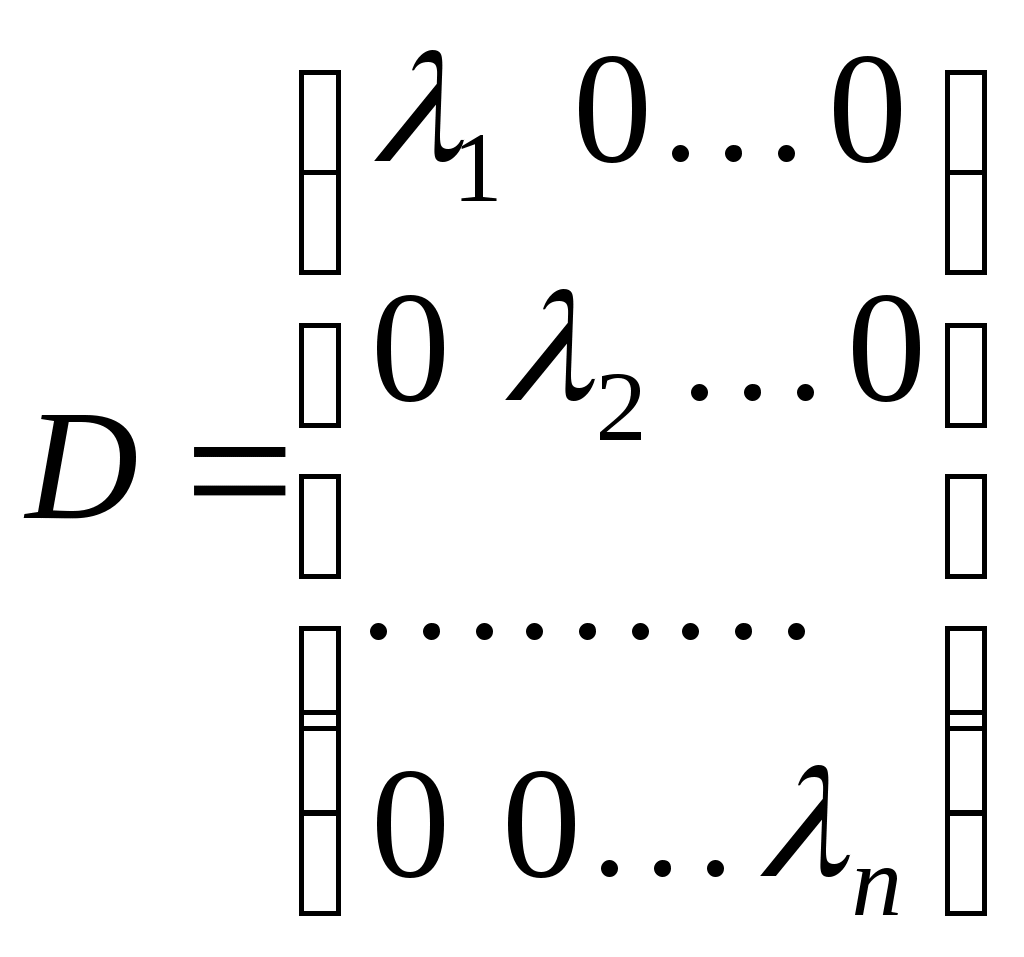 .
.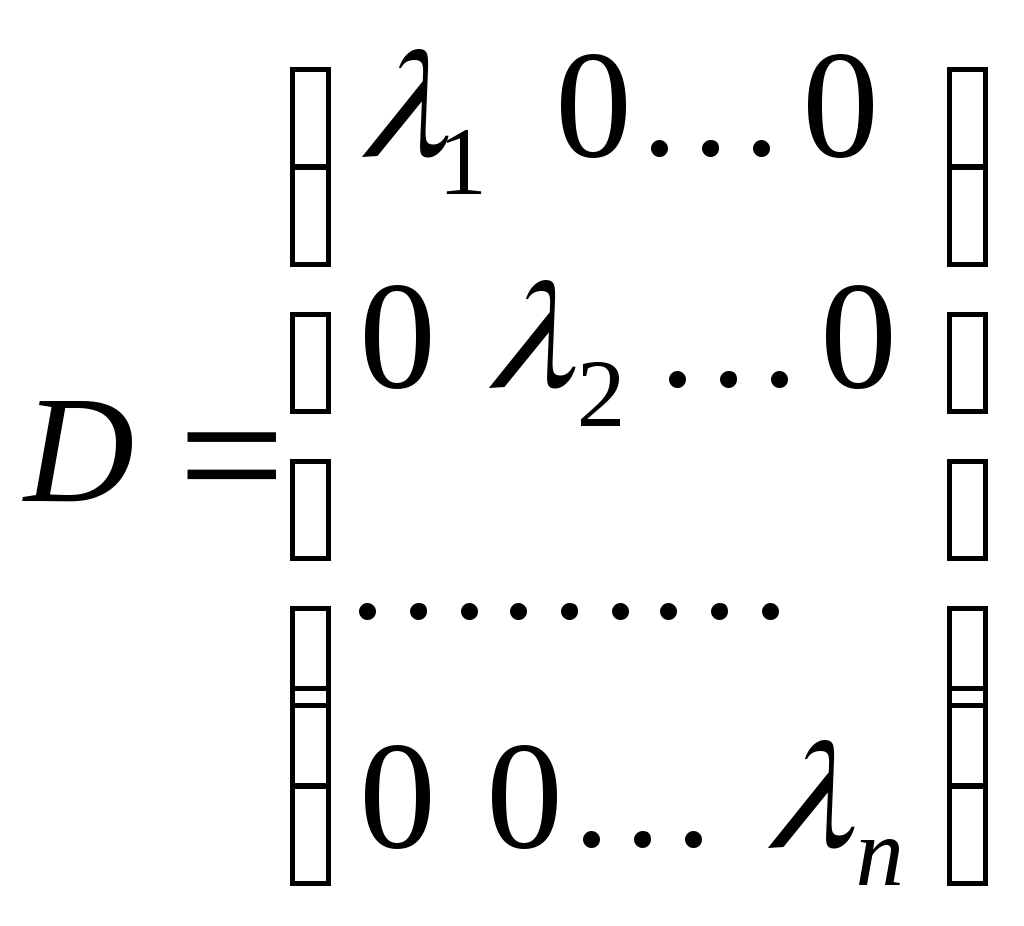 ,
,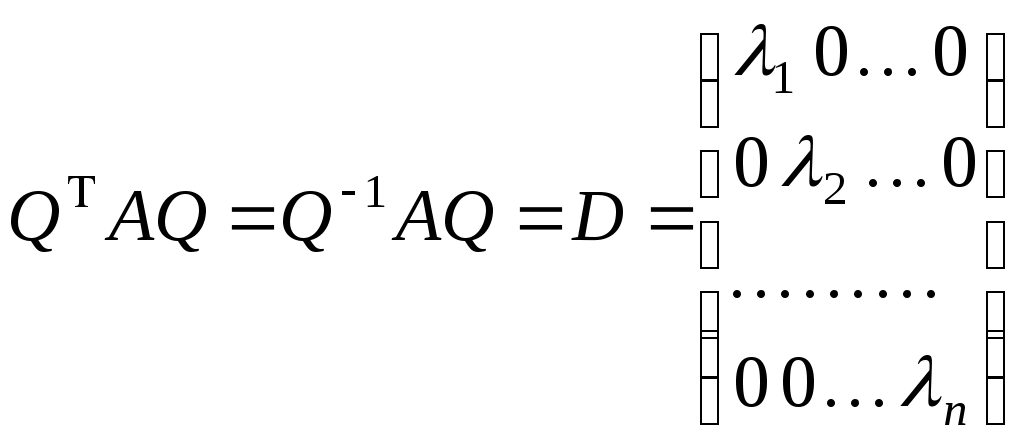 .
.