|
|
Билинейные формы Шестаков. Білінійні та квадратичні функції С. С. Шестаков. Конспект лекцій для студентів заочного відділенння
Метод Якобі
Нехай  - квадратна матриця порядку - квадратна матриця порядку  . Кутовим мінором порядку . Кутовим мінором порядку 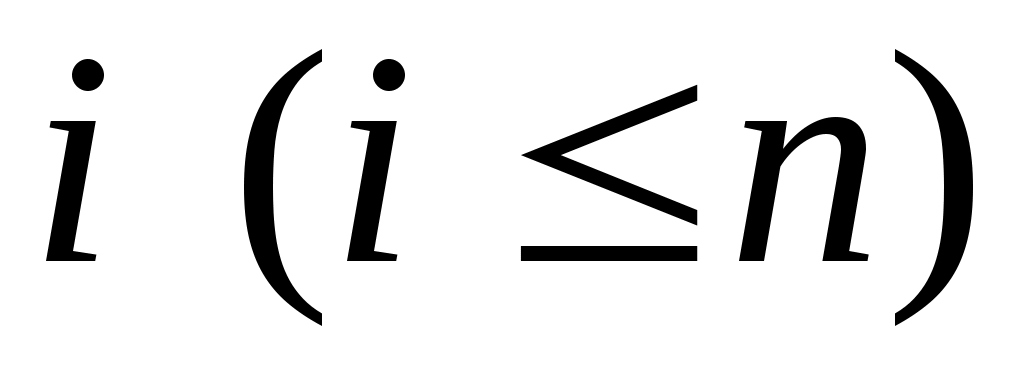 матриці матриці  називається мінор називається мінор 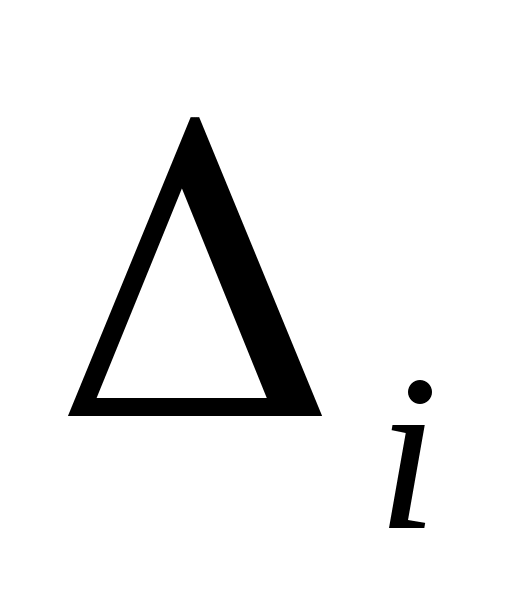 , побудований на перших , побудований на перших 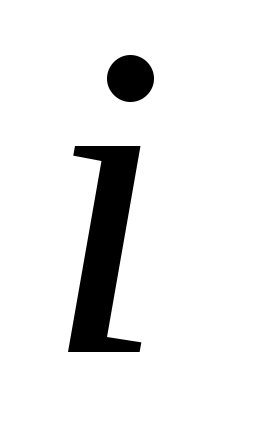 рядках та рядках та 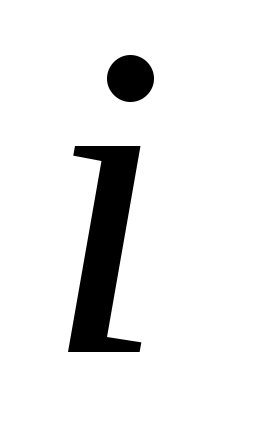 стовпчиках матриці стовпчиках матриці  . .
Наприклад, 
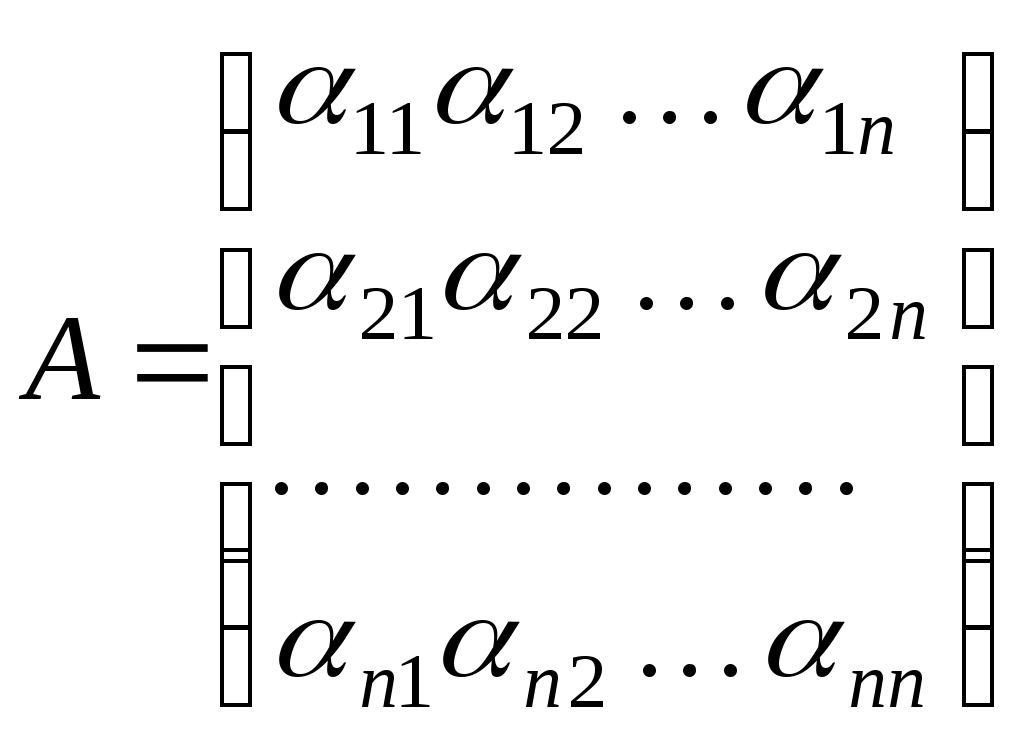 , ,
тоді
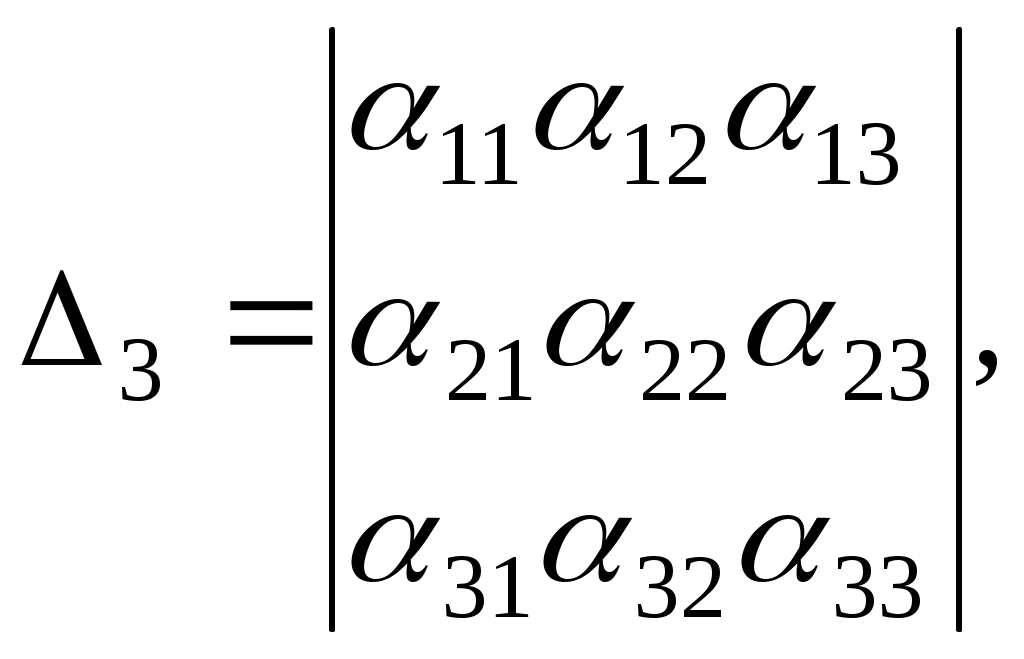 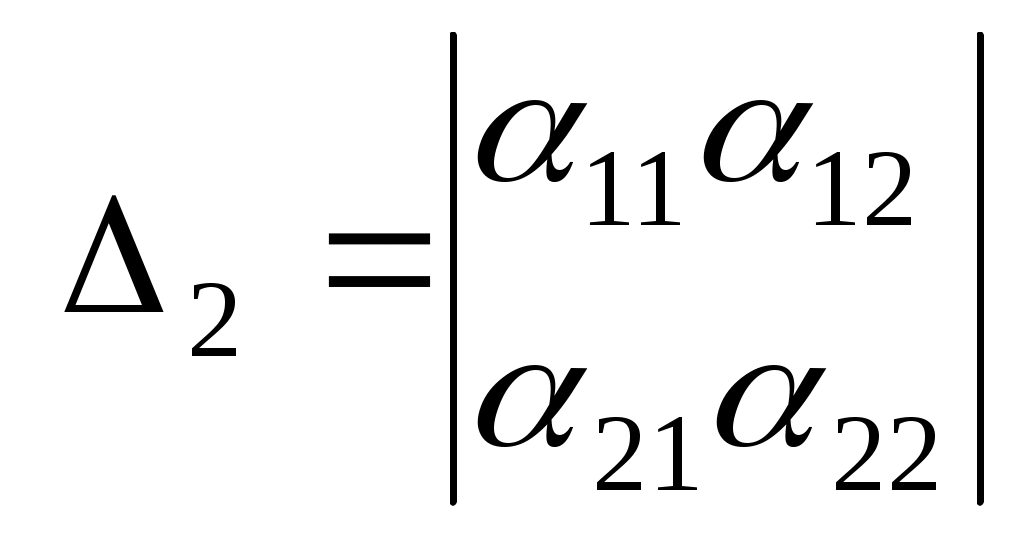 , , 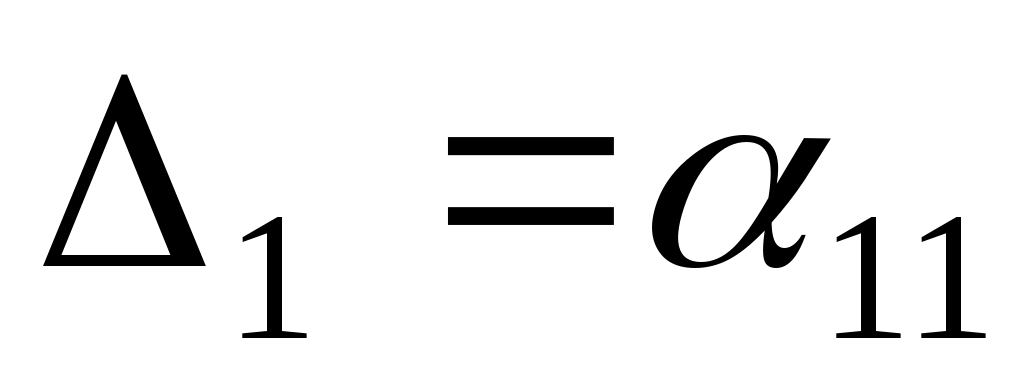 , , 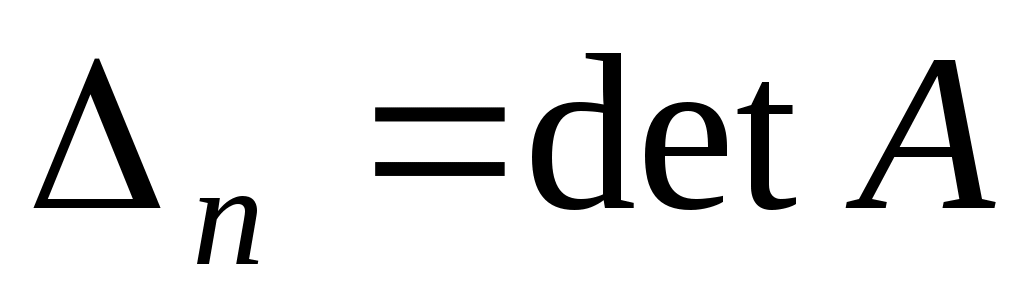 . .
Будемо казати, що матриця  задовольняє умову Якобі, якщо всі її кутові мінори не дорівнюють нулю. задовольняє умову Якобі, якщо всі її кутові мінори не дорівнюють нулю.
Теорема Якобі (критерій Якобі). Нехай квадратична функція 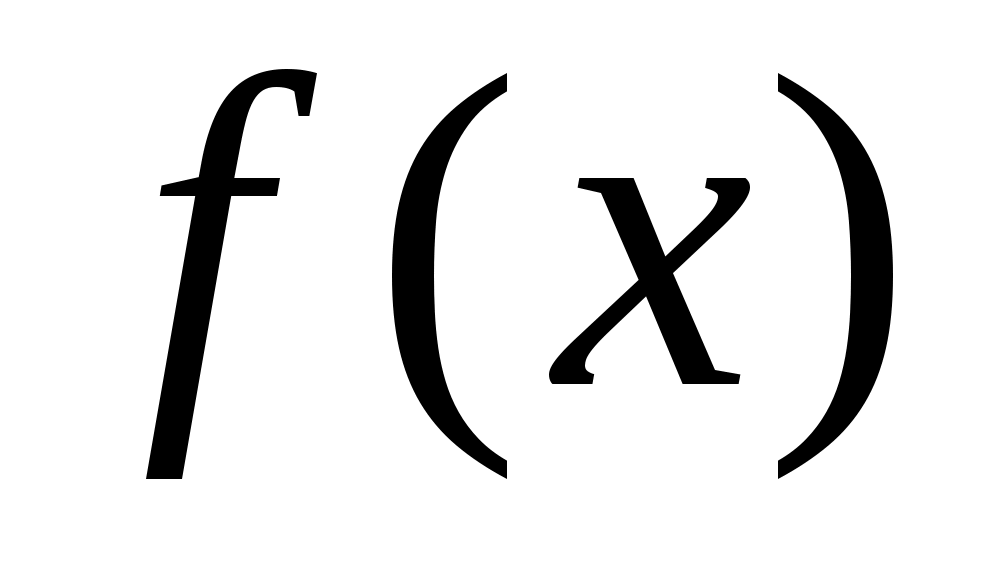 на скінченновимірному векторному просторі на скінченновимірному векторному просторі  у деякому базисі задається матрицею у деякому базисі задається матрицею  , яка задовольняє умову Якобі. Тоді в просторі , яка задовольняє умову Якобі. Тоді в просторі  існує базис, у якому функції існує базис, у якому функції  відповідає квадратична форма: відповідає квадратична форма:
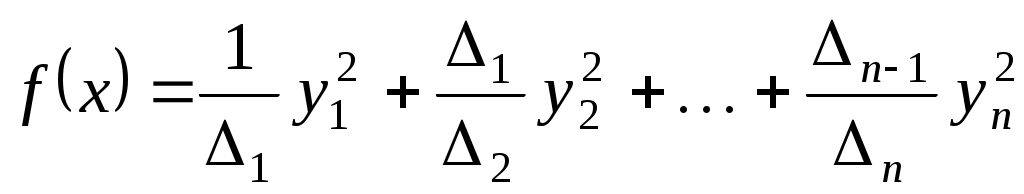 , ,
де 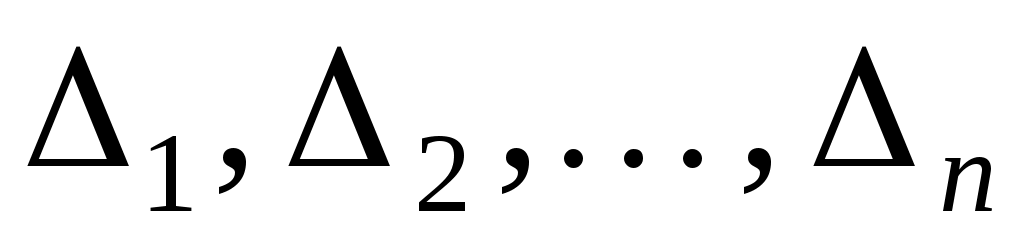 - всі кутові мінори матриці - всі кутові мінори матриці  . .
Доведення. Припустимо, що в базисі 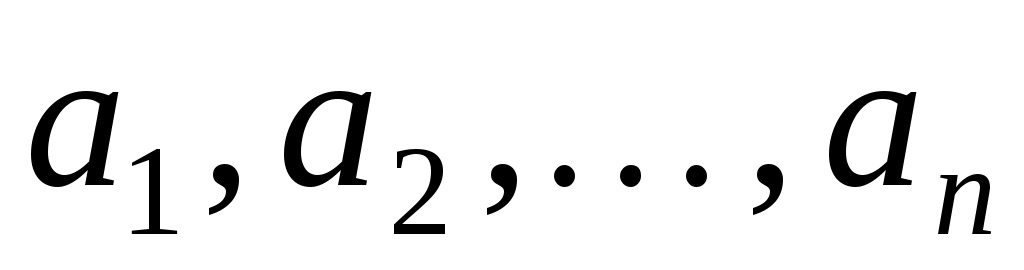 простору простору  квадратичній квадратичній
функції  відповідає матриця відповідає матриця
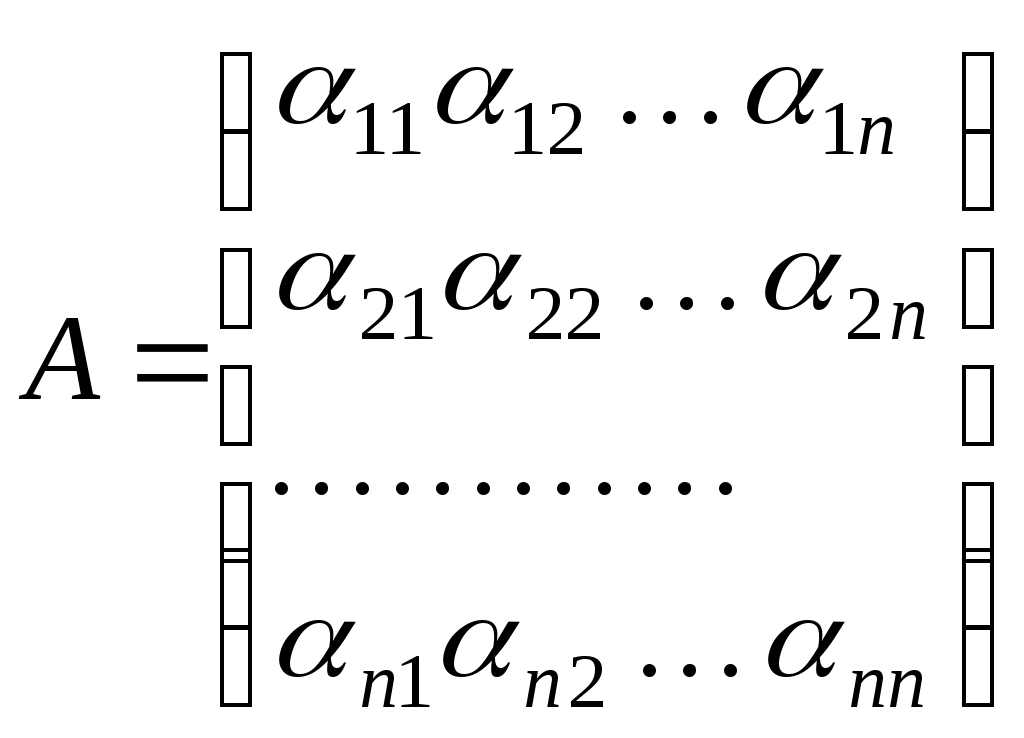 , ,
яка задовольняє умову Якобі . Через  позначимо полярну симетричну білінійну функцію, яка породжує квадратичну функцію позначимо полярну симетричну білінійну функцію, яка породжує квадратичну функцію  . Новий базис . Новий базис  простору будемо шукати у вигляді простору будемо шукати у вигляді
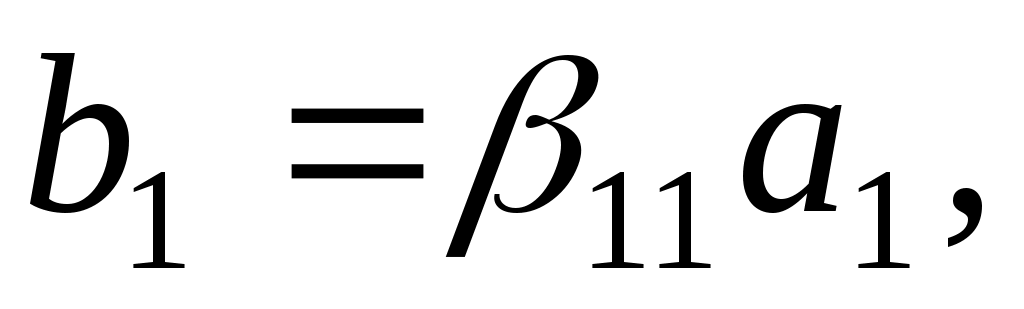
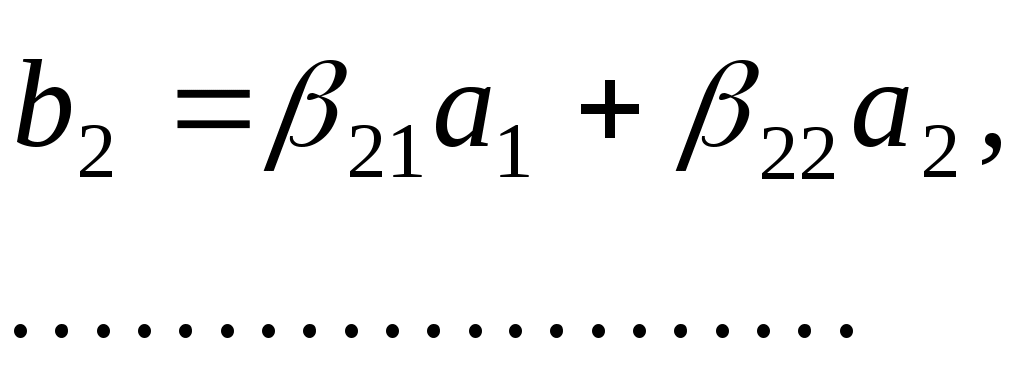
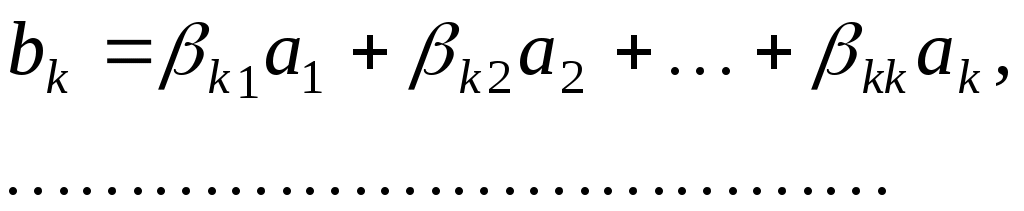
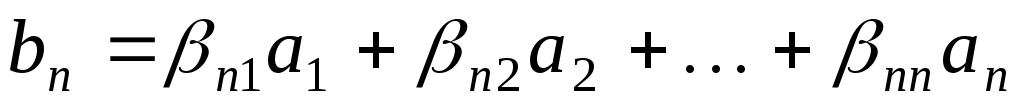 . .
Для знаходження коефіцієнтів  припустимо, що вектори припустимо, що вектори  задовольняють умови задовольняють умови
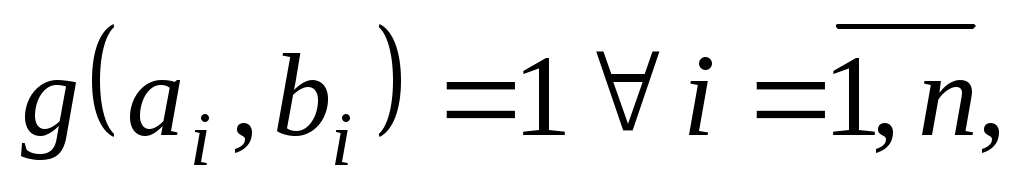
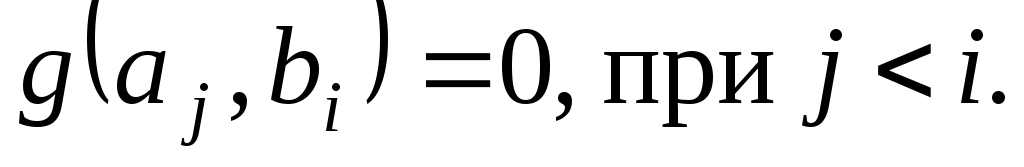
Знайдемо спочатку вектор 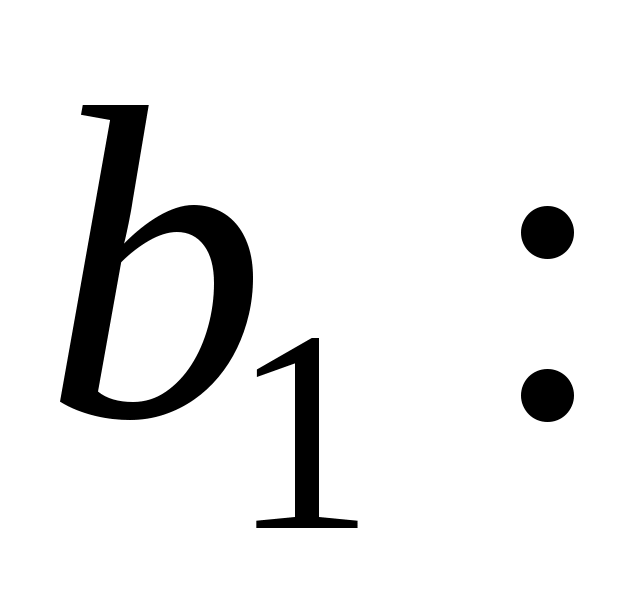
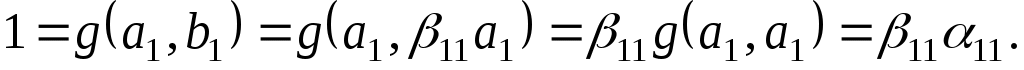
Оскільки 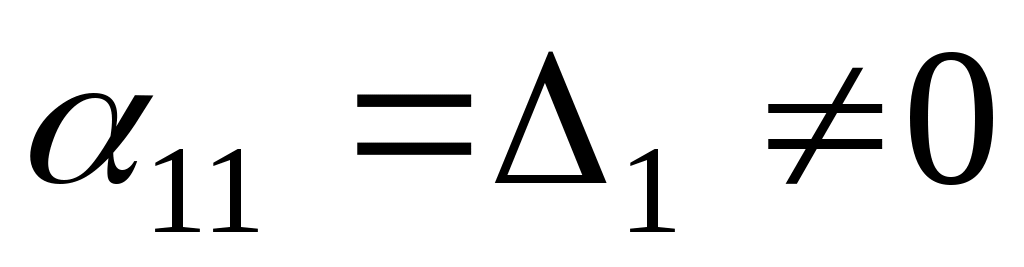 , то , то 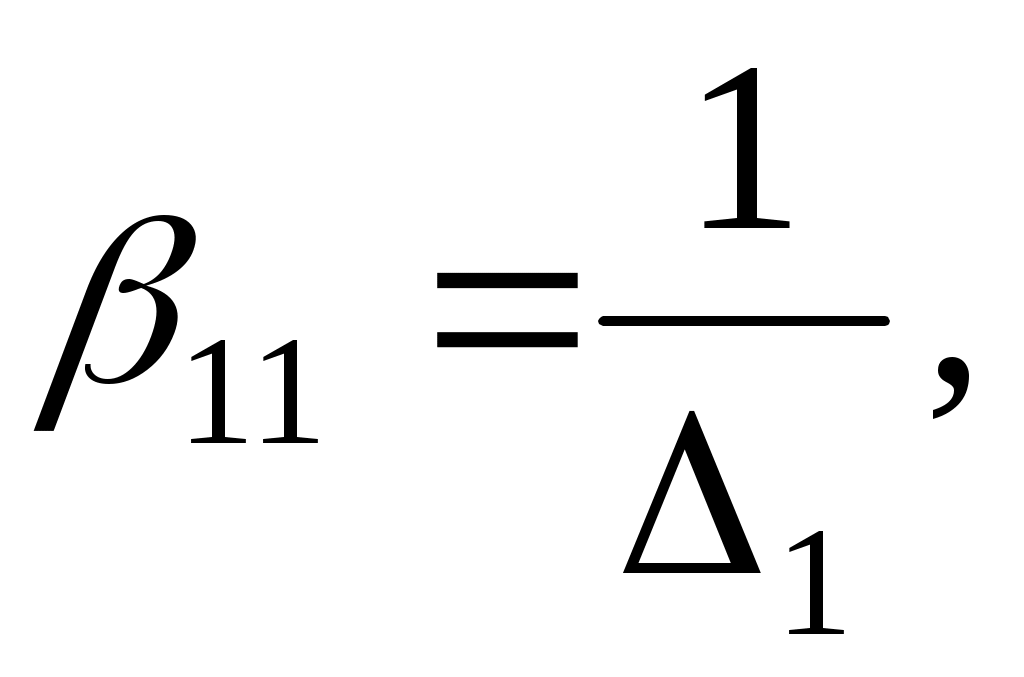 а тому а тому
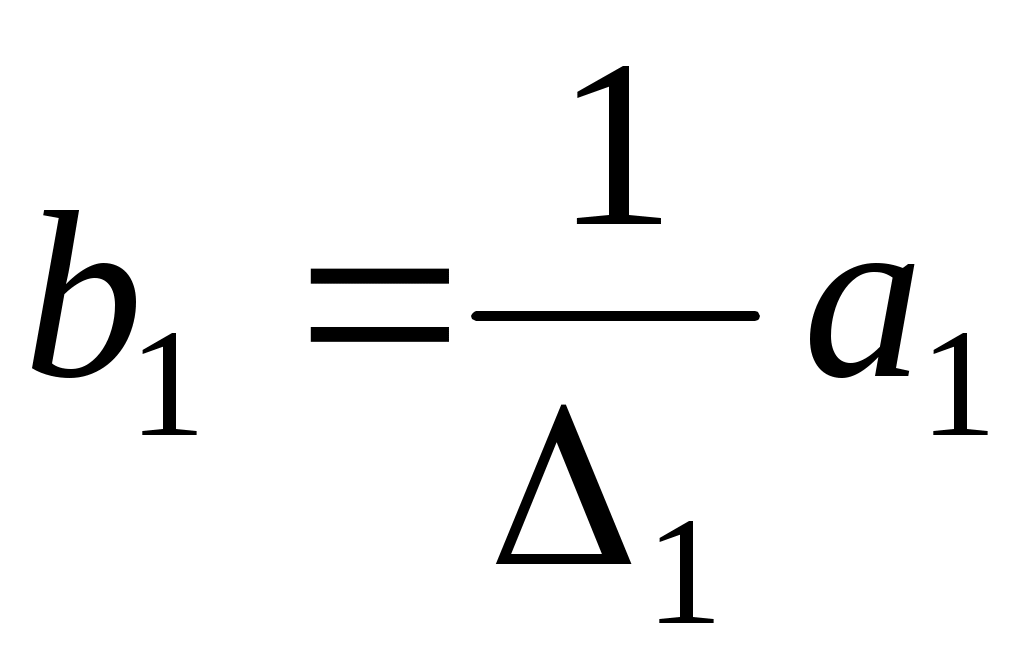 . .
Припустимо тепер, що вже знайдено вектори 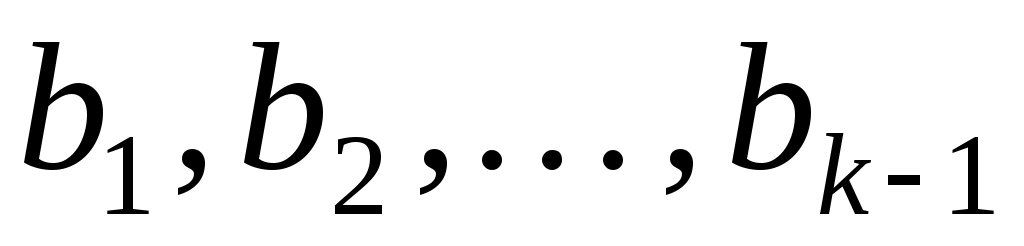 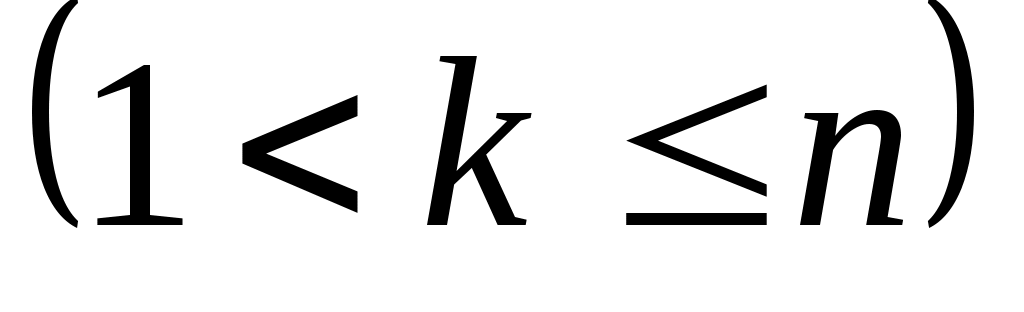 , і знайдемо вектор , і знайдемо вектор 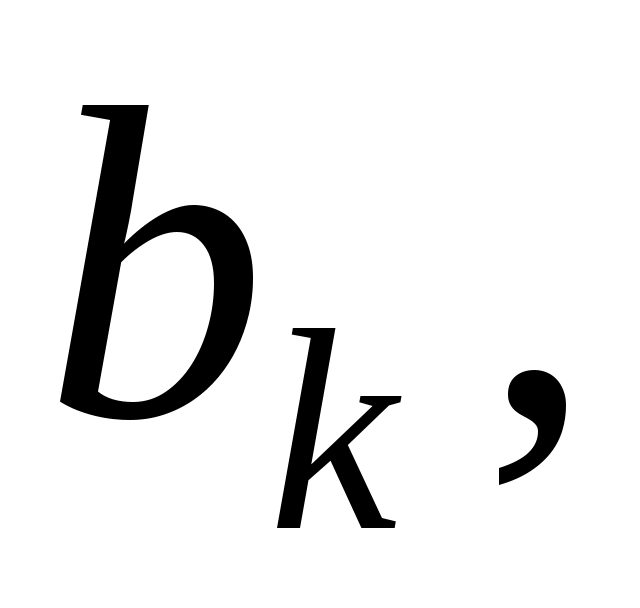 скориставшись умовами скориставшись умовами
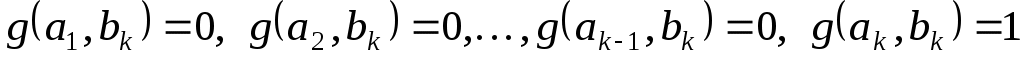 . .
Це означає, що 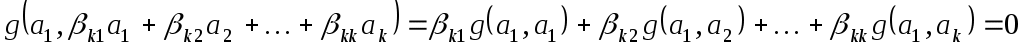
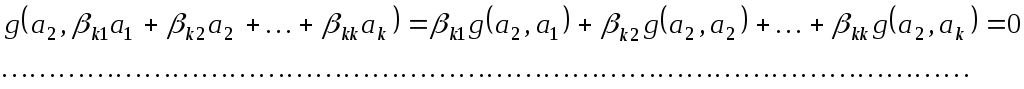
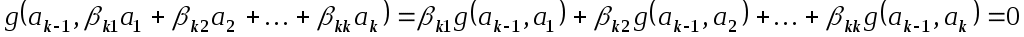
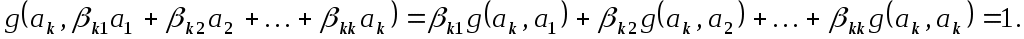
Оскільки 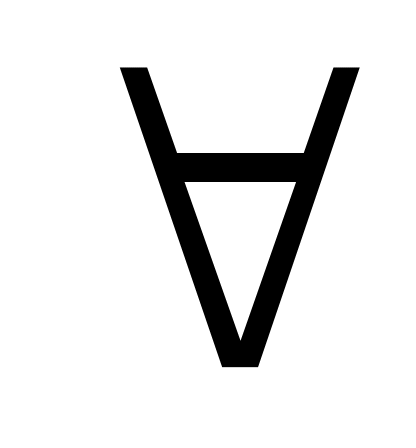 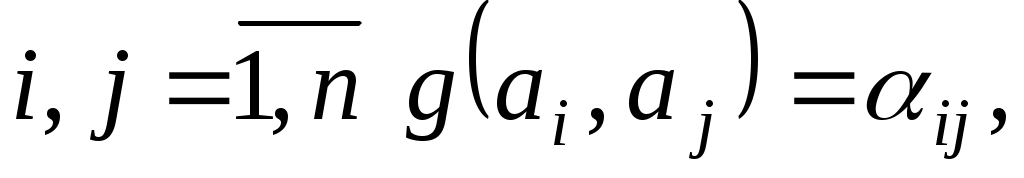 то ці рівності можна переписати так: то ці рівності можна переписати так:
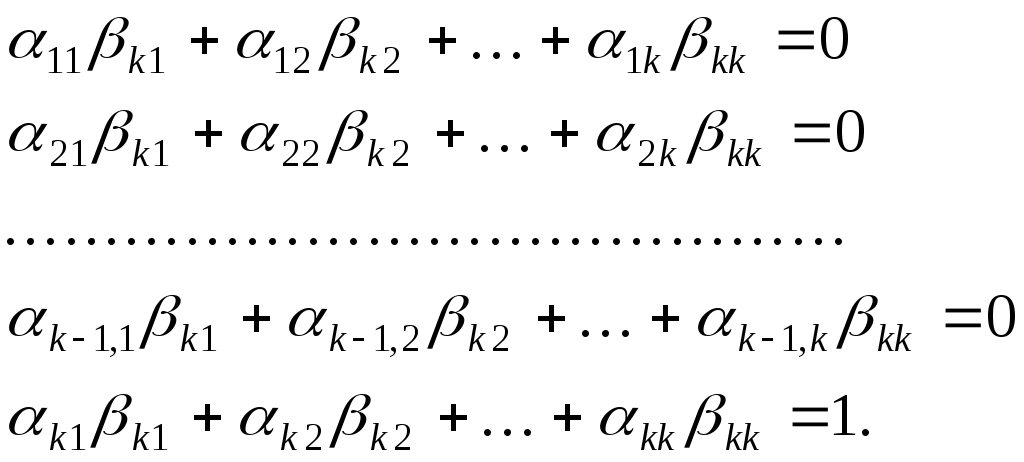
Ми одержали систему лінійних рівнянь відносно невідомих 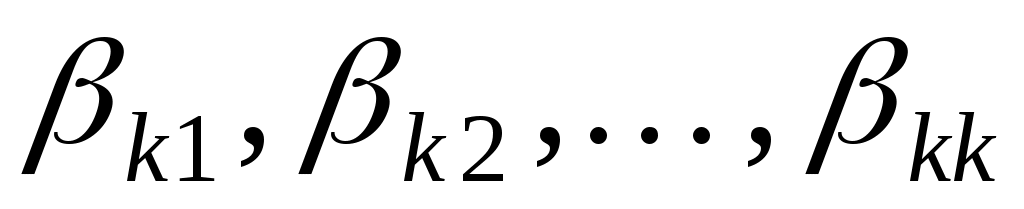 . Система квадратна, її головний визначник . Система квадратна, її головний визначник 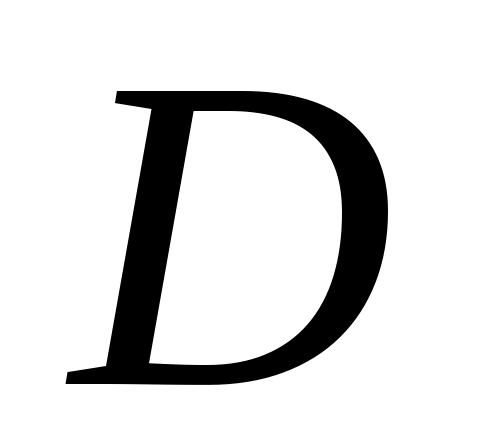 співпадає з кутовим мінором співпадає з кутовим мінором 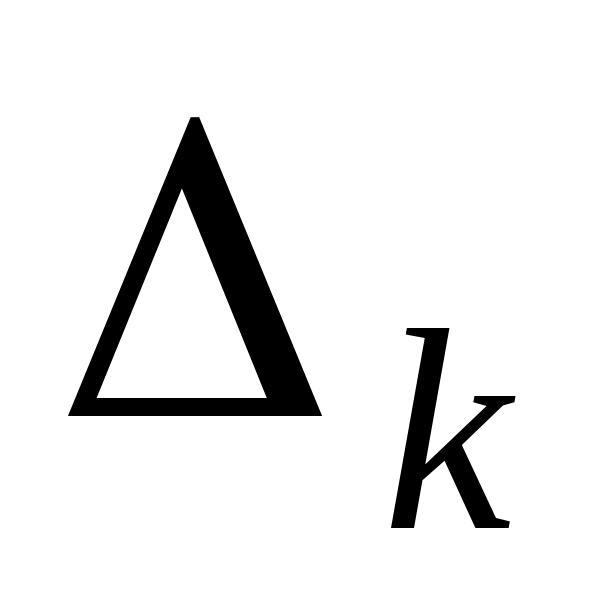 матриці матриці  . Тобто, . Тобто, 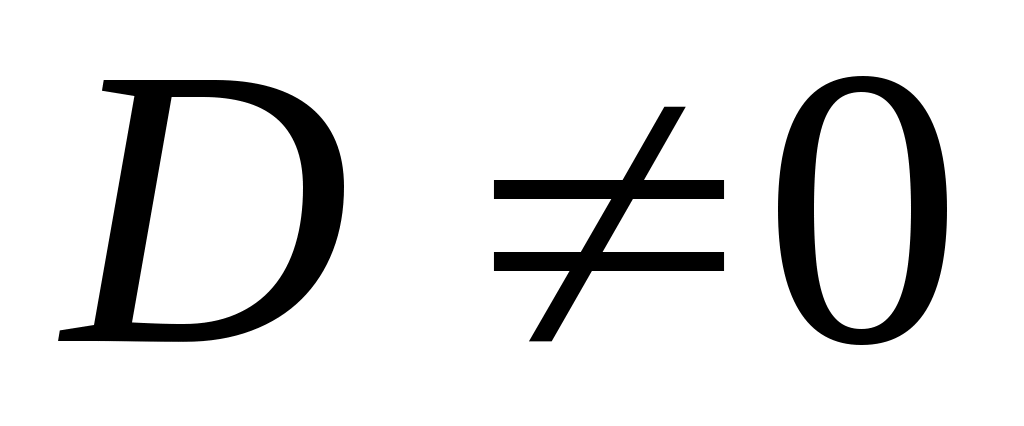 , за умовою теореми. Система має єдиний розв’язок, за теоремою Крамера, - , за умовою теореми. Система має єдиний розв’язок, за теоремою Крамера, - 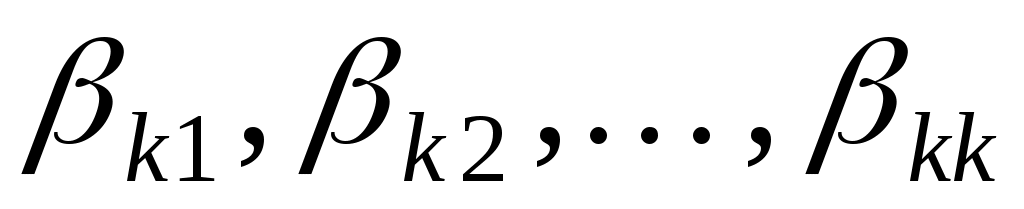 , ці значення визначають вектор , ці значення визначають вектор 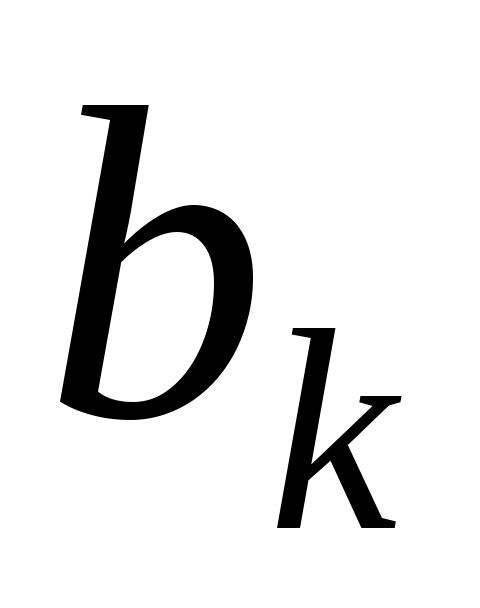 . Знайдемо . Знайдемо 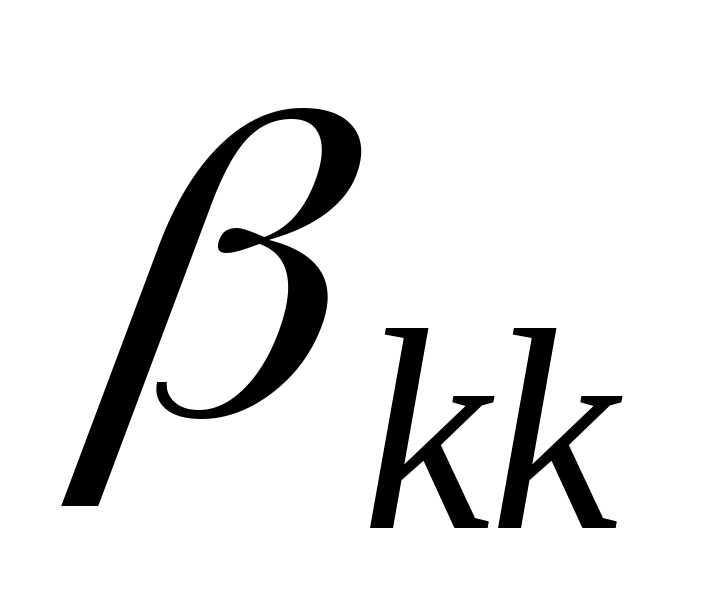 за формулою Крамера: за формулою Крамера:
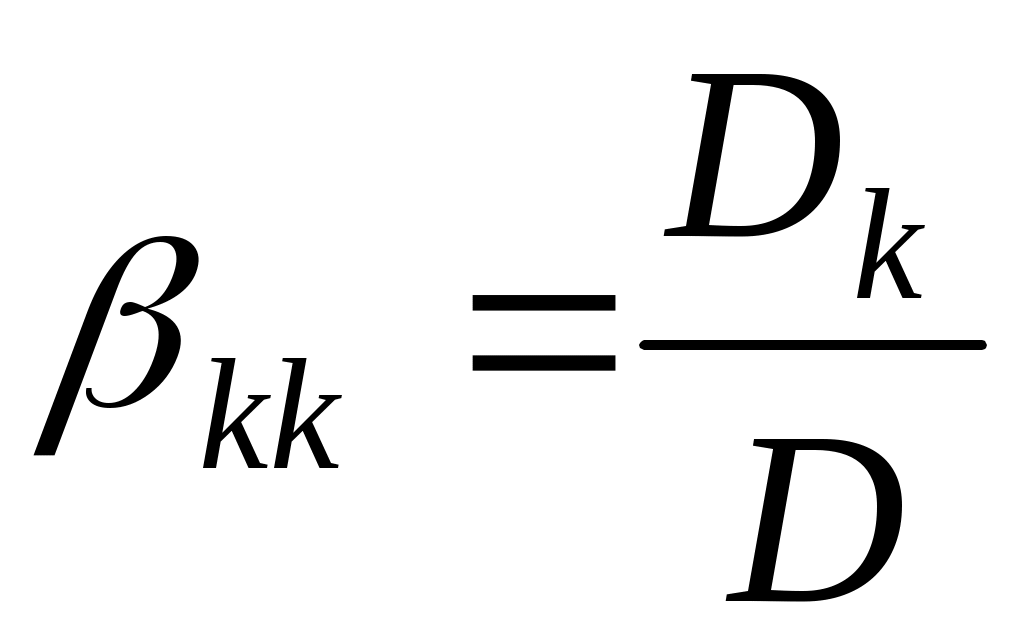 , ,
де 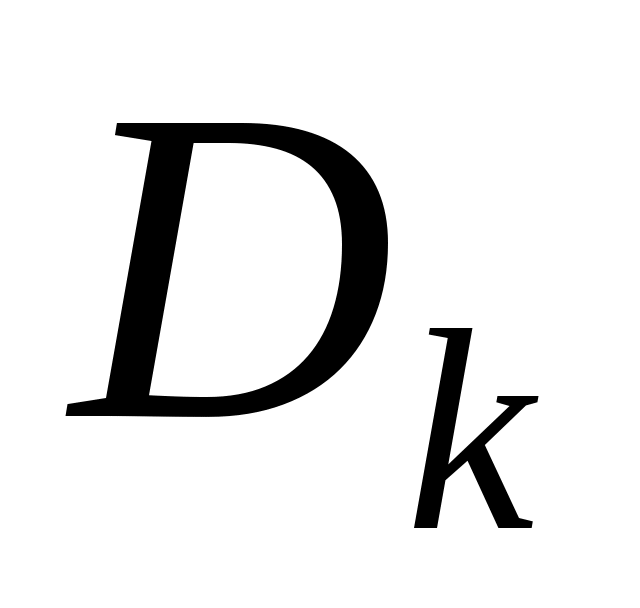 - визначник, який одержується з визначника - визначник, який одержується з визначника 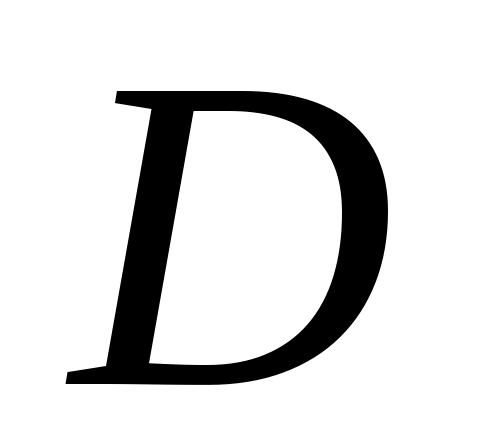 заміною заміною 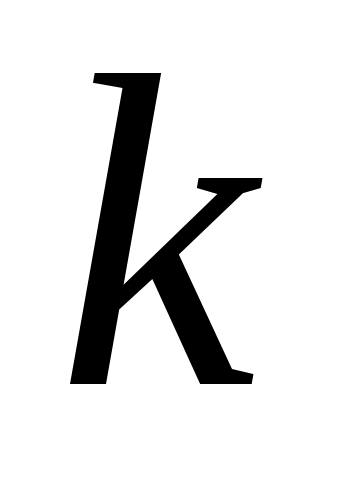 -го стовпчика на -го стовпчика на
стовпчик вільних членів. Але
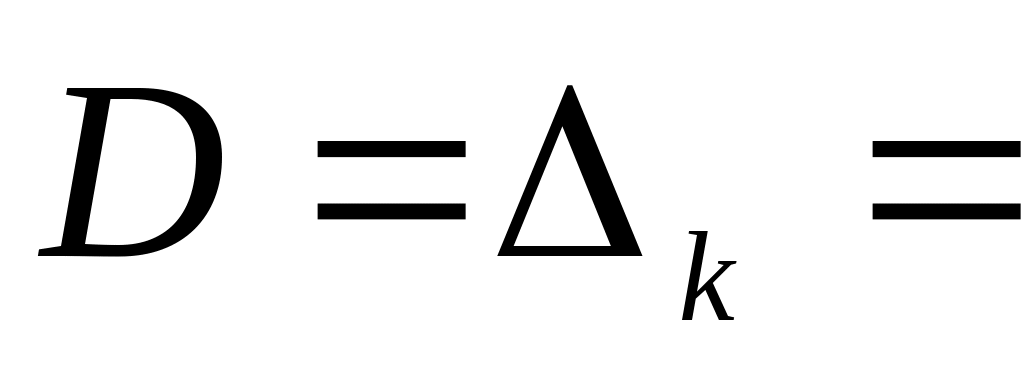 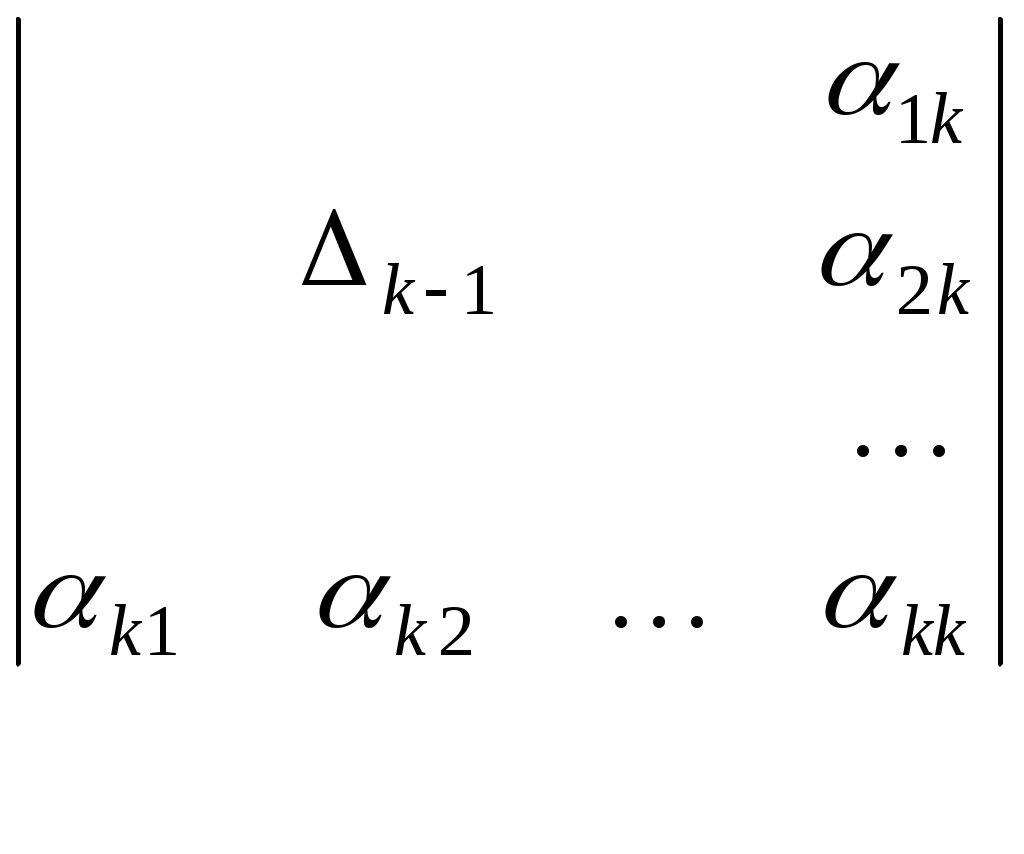 , ,
тоді
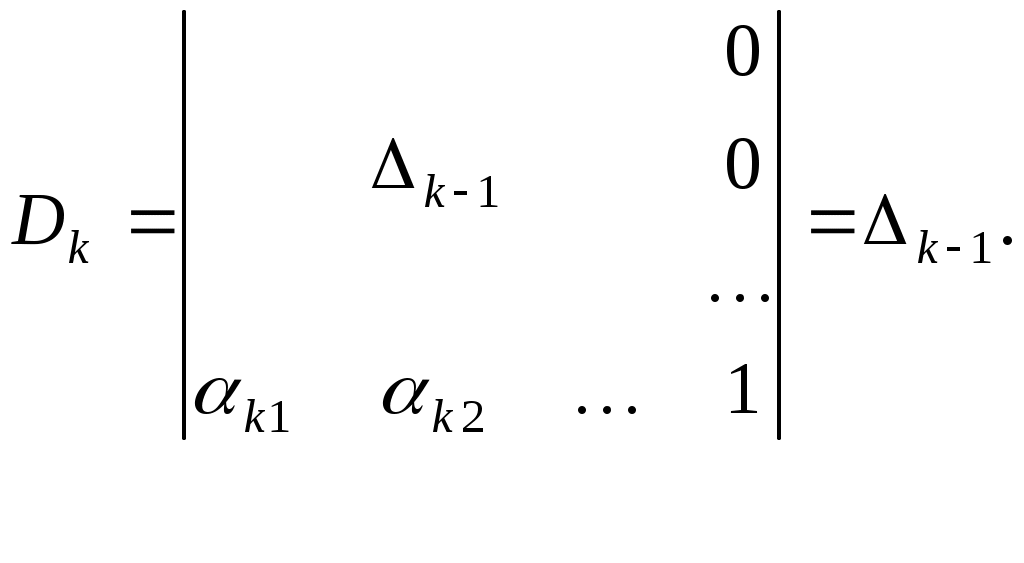
Тому
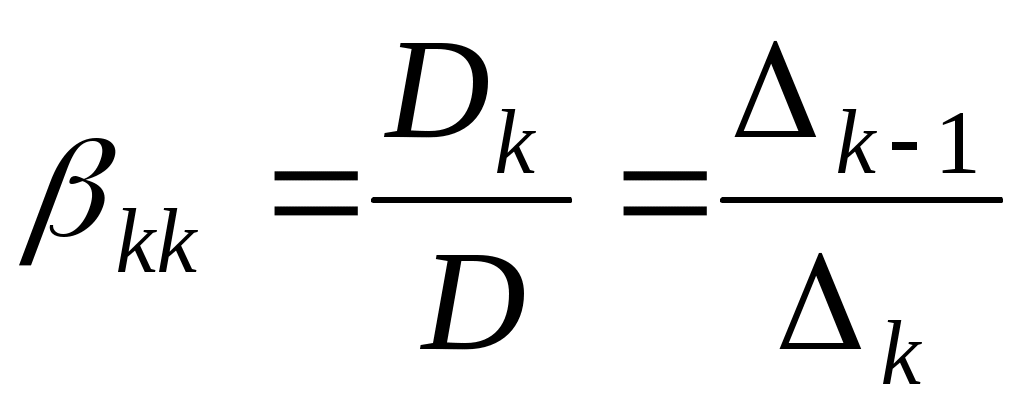 . .
Доведемо тепер, що вектори  утворюють базис простору. Оскільки кількість векторів у цій системі співпадає з розмірністю простору, то достатньо довести лінійну незалежність цієї системи. Припустимо супротивне. Тобто, нехай ці вектори лінійно залежні. Оскільки утворюють базис простору. Оскільки кількість векторів у цій системі співпадає з розмірністю простору, то достатньо довести лінійну незалежність цієї системи. Припустимо супротивне. Тобто, нехай ці вектори лінійно залежні. Оскільки
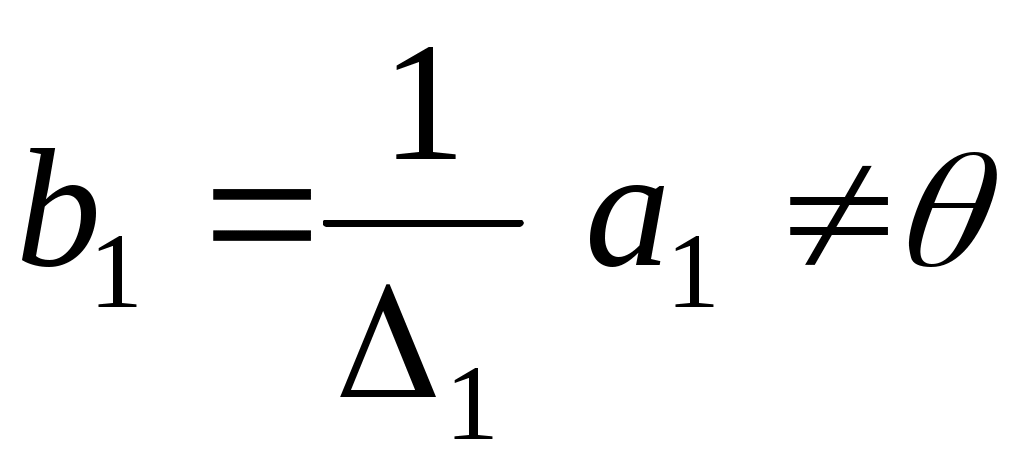 , ,
це означає, що деякий вектор 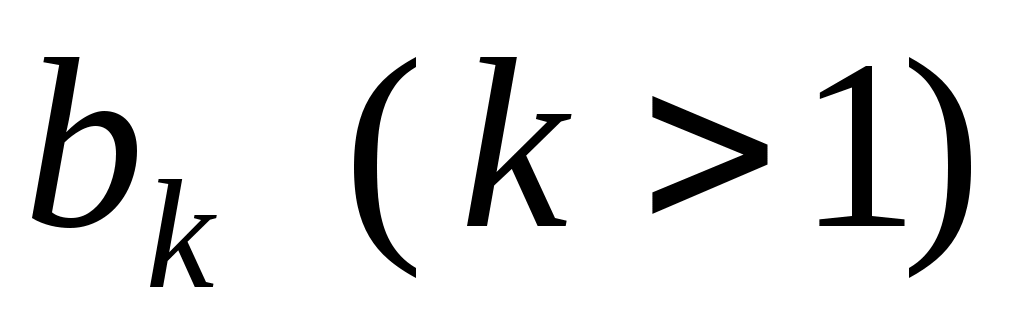 лінійно виражається через попередні вектори системи лінійно виражається через попередні вектори системи 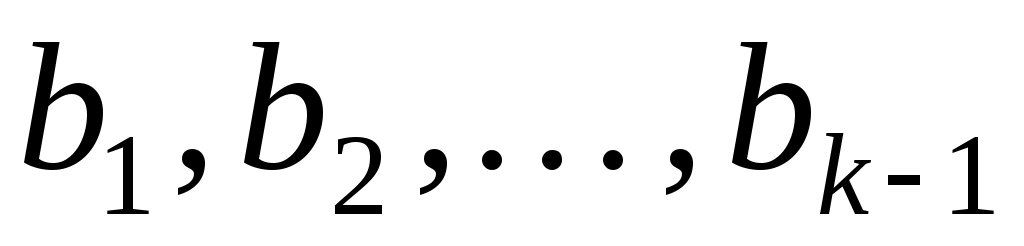 , тобто, , тобто,
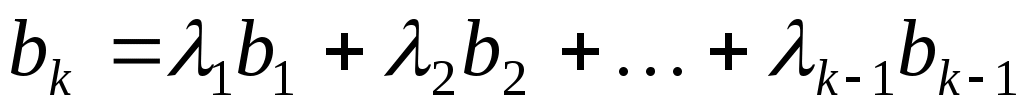 . .
Але для кожного індексу 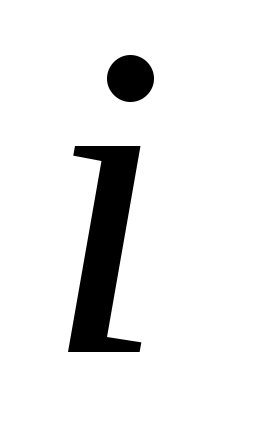 вектор вектор 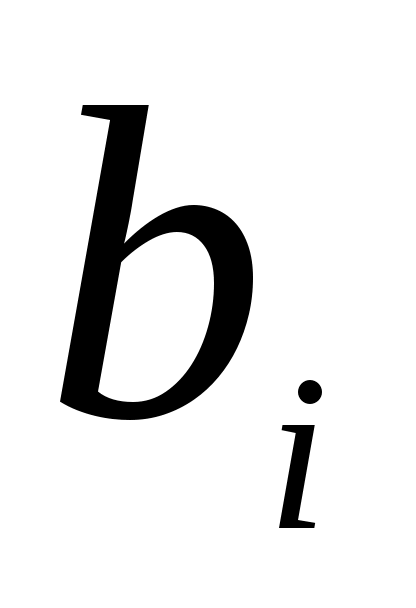 лінійно виражається лише через вектори лінійно виражається лише через вектори 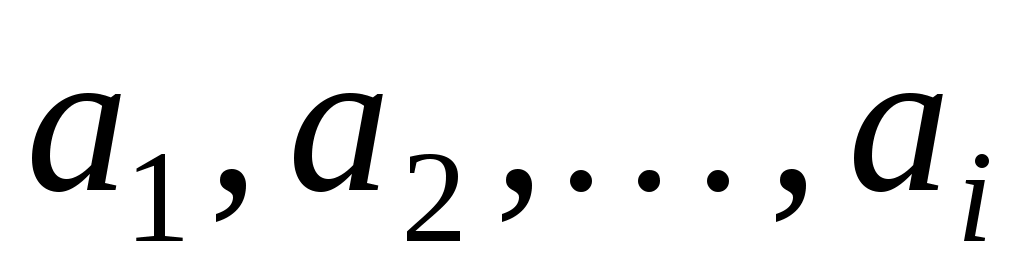 , тоді вектор , тоді вектор 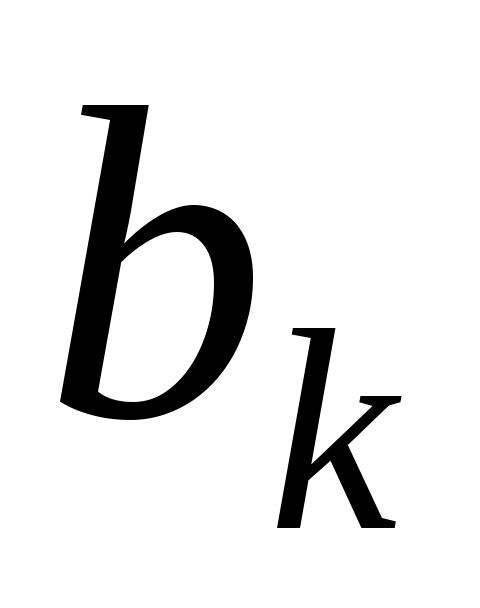 можна лінійно виразити через вектори можна лінійно виразити через вектори 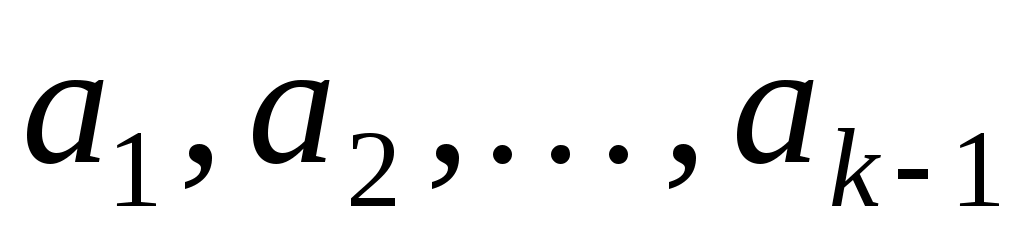 : :
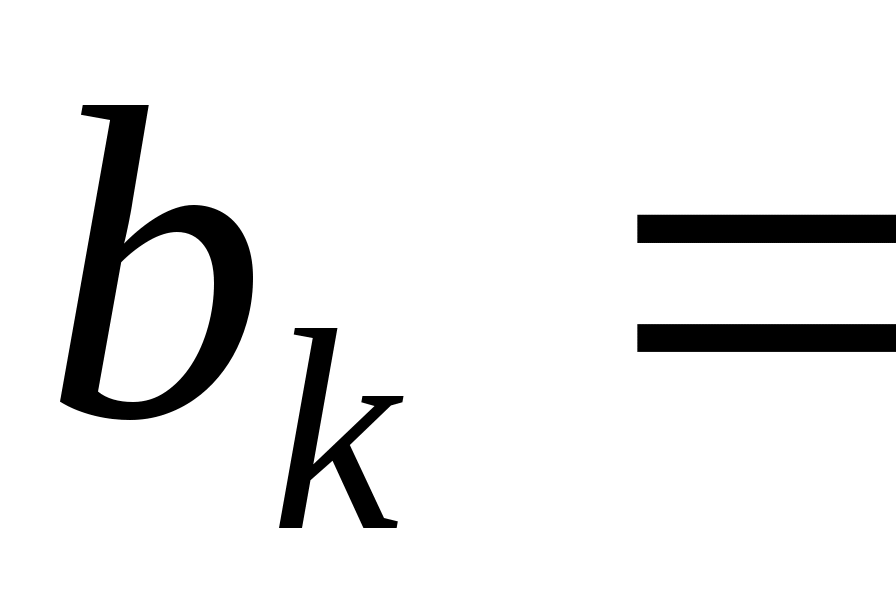 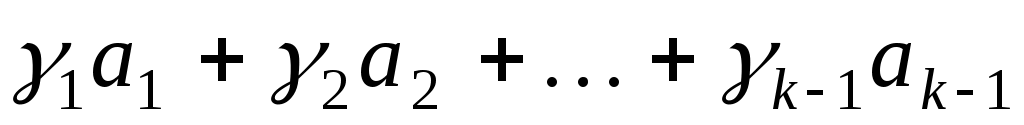
для деяких 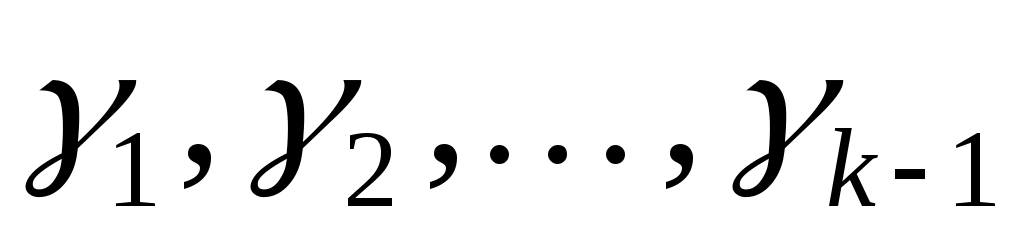 . Отже, . Отже,
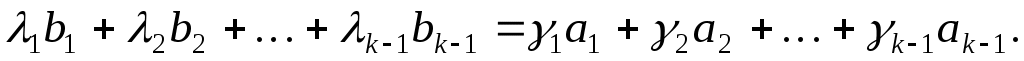
Тоді
 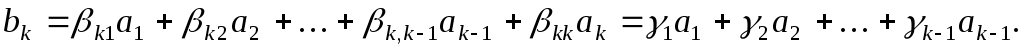
Оскільки
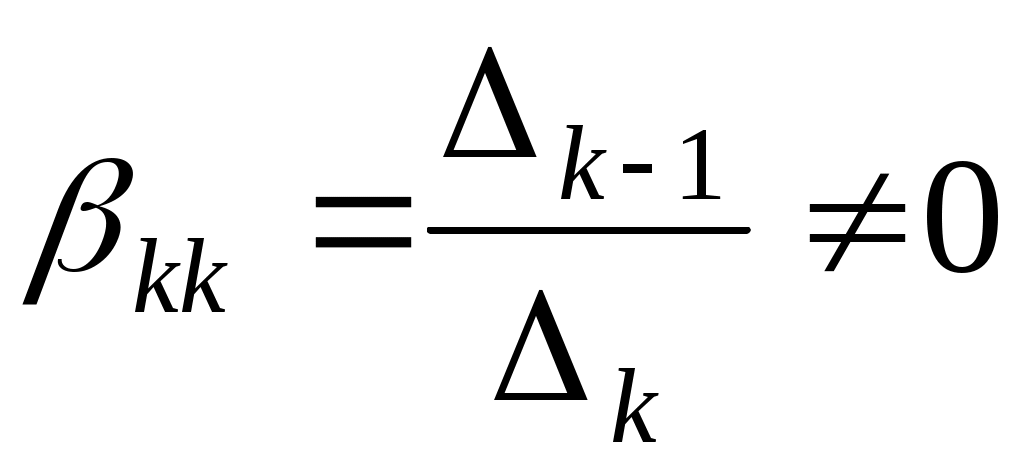 , ,
то з останньої рівності вектор 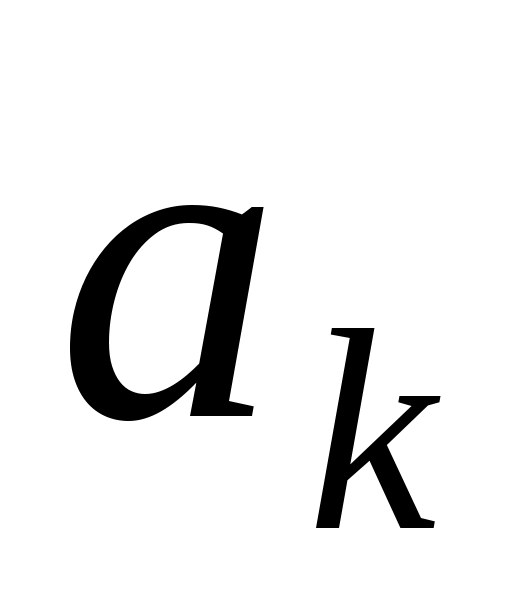 можна лінійно виразити через вектори можна лінійно виразити через вектори 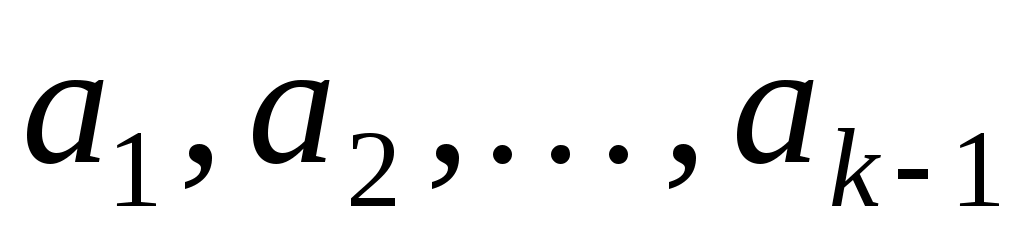 . Цього бути не може, оскільки вектори . Цього бути не може, оскільки вектори  утворюють базис простору. Таким чином, припущення було не вірним, а тому вектори утворюють базис простору. Таким чином, припущення було не вірним, а тому вектори  лінійно незалежні і також утворюють базис простору. лінійно незалежні і також утворюють базис простору.
Знайдемо матрицю 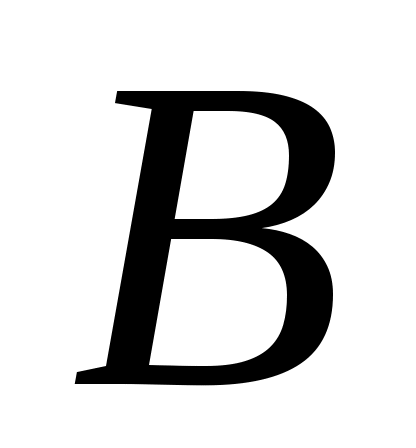 квадратичної функції квадратичної функції  у базисі у базисі  . Припустимо спочатку, що . Припустимо спочатку, що 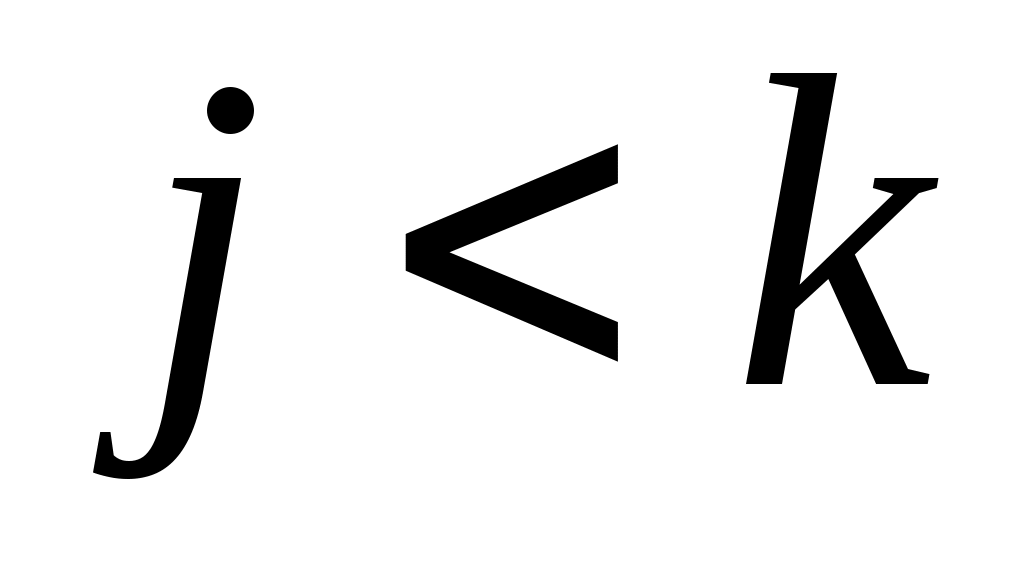 , і, враховуючи принцип побудови векторів , і, враховуючи принцип побудови векторів  , одержуємо: , одержуємо:
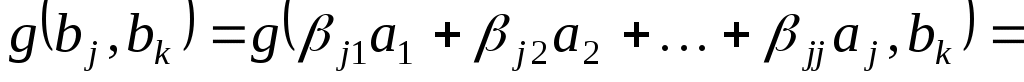
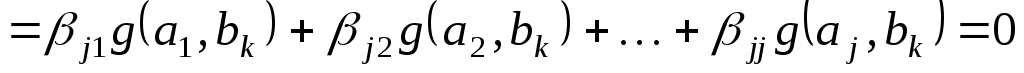 . .
Оскільки матриця  симетрична, звідси випливає, що всі її елементи, що стоять поза головною діагоналлю, дорівнюють нулю. Тобто, матриця симетрична, звідси випливає, що всі її елементи, що стоять поза головною діагоналлю, дорівнюють нулю. Тобто, матриця  діагональна. діагональна.
Знайдемо тепер діагональні елементи:
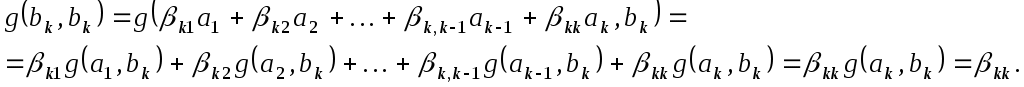
Таким чином,
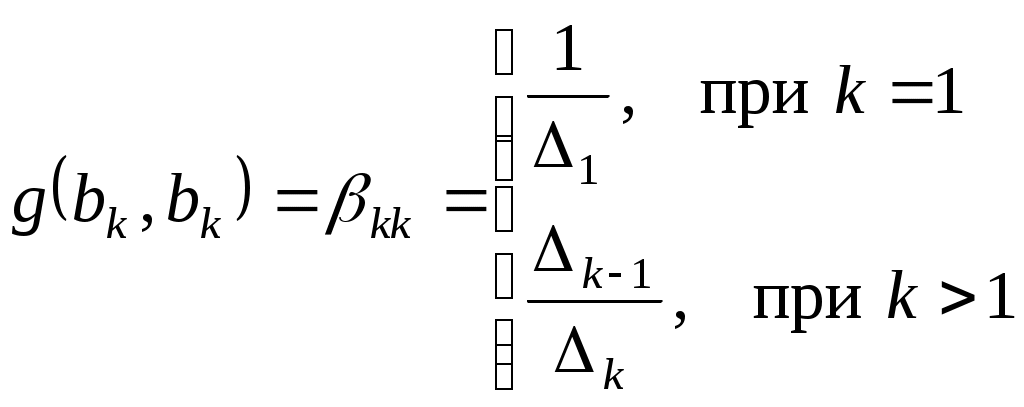 . .
Тобто, матриця має такий вигляд:
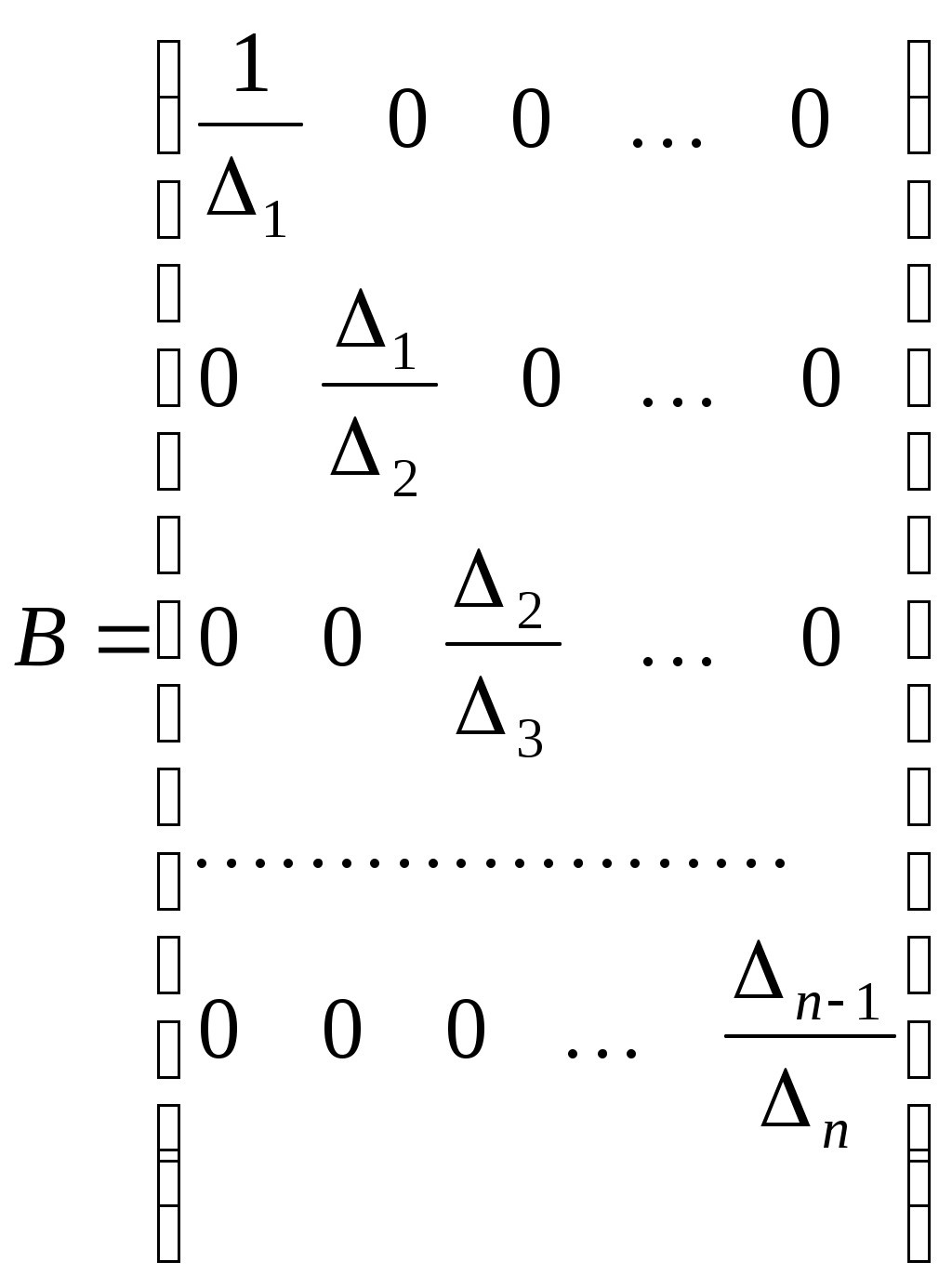 . .
Якщо довільний вектор  у базисі у базисі  задається такими координатами: задається такими координатами: 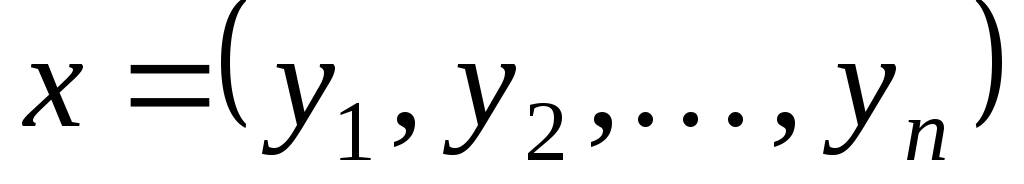 , то , то
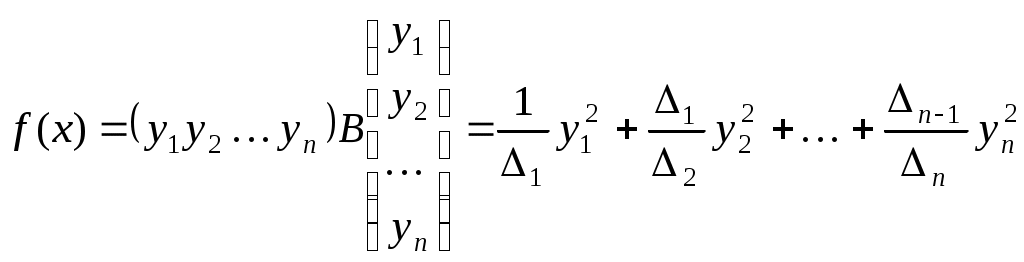 . .
Тобто, в базисі  квадратична функція квадратична функція  задається такою канонічною квадратичною формою: задається такою канонічною квадратичною формою:
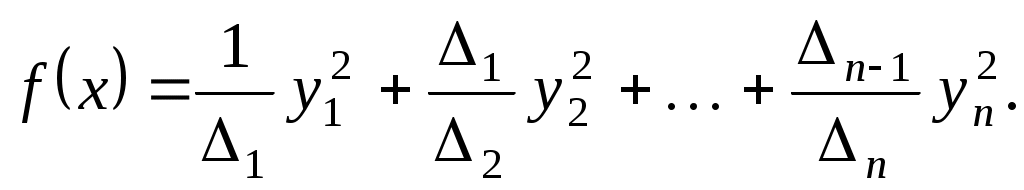
Закон інерції квадратичних форм
Нехай  - квадратична функція на скінченновимірному векторному просторі - квадратична функція на скінченновимірному векторному просторі  над полем над полем  . Тоді в будь-якому базисі простору вона задається деякою квадратичною формою. Квадратичну функцію можна звести до канонічного вигляду. Це означає, що шукається базис, у якому функція . Тоді в будь-якому базисі простору вона задається деякою квадратичною формою. Квадратичну функцію можна звести до канонічного вигляду. Це означає, що шукається базис, у якому функція  задається канонічною квадратичною формою. Але цей базис можна знайти різними способами. Тому для даної квадратичної функції існує багато таких базисів і багато канонічних квадратичних форм. Але для всіх цих форм виконується закон інерції квадратичних форм. задається канонічною квадратичною формою. Але цей базис можна знайти різними способами. Тому для даної квадратичної функції існує багато таких базисів і багато канонічних квадратичних форм. Але для всіх цих форм виконується закон інерції квадратичних форм.
Теорема (закон інерції квадратичних форм). Незалежно від способу зведення квадратичної функції на скінченновимірному просторі до канонічного вигляду у відповідних канонічних квадратичних формах число додатних коефіцієнтів, число від’ємних коефіцієнтів, а тому і число ненульових є величинами сталими.
Доведення. Нехай  - квадратична функція на скінченновимірному просторі - квадратична функція на скінченновимірному просторі  , , 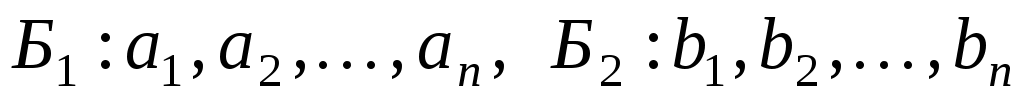 - базиси простору, в яких функція - базиси простору, в яких функція  задається канонічними квадратичними формами. Припустимо, що в базисі задається канонічними квадратичними формами. Припустимо, що в базисі 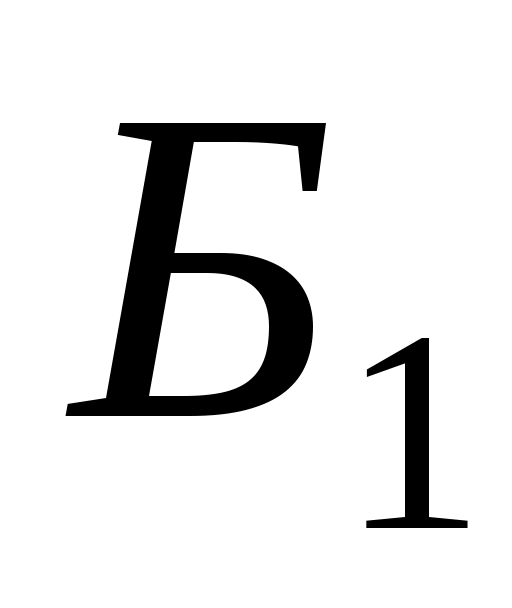 функції функції  відповідає квадратична форма: відповідає квадратична форма:
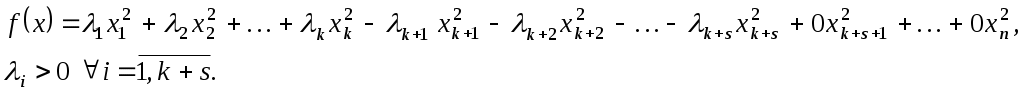
 У базисі У базисі 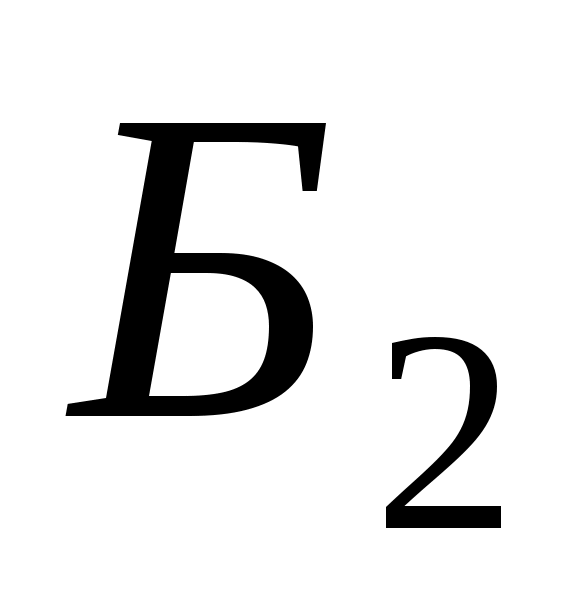 функції функції  відповідає квадратична форма: відповідає квадратична форма:
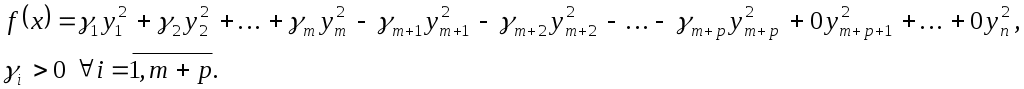
Доведемо, що 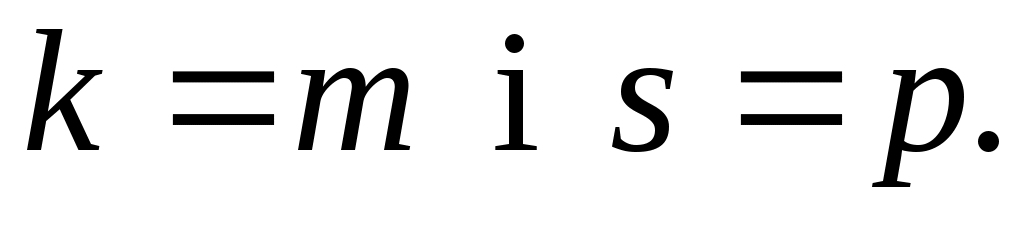
Покажемо спочатку, що 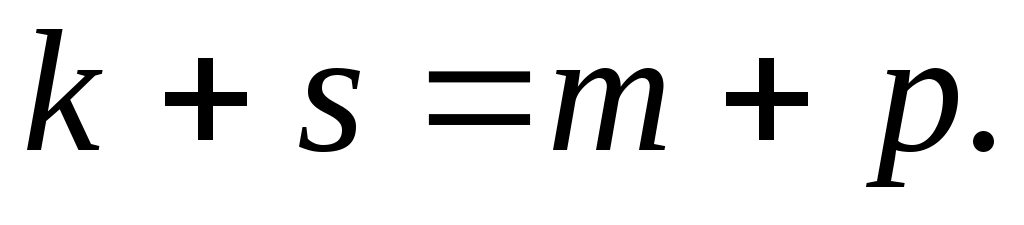 Оскільки в базисі Оскільки в базисі 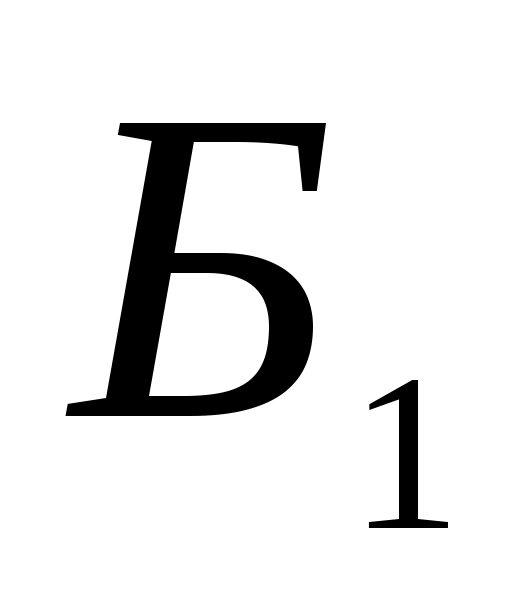 квадратична функція квадратична функція  задається канонічною квадратичною формою, то в цьому базисі матриця квадратичної функції діагональна. На діагоналі матриці стоять коефіцієнти при квадратах змінних у квадратичній формі. Тобто, ранг цієї матриці дорівнює задається канонічною квадратичною формою, то в цьому базисі матриця квадратичної функції діагональна. На діагоналі матриці стоять коефіцієнти при квадратах змінних у квадратичній формі. Тобто, ранг цієї матриці дорівнює 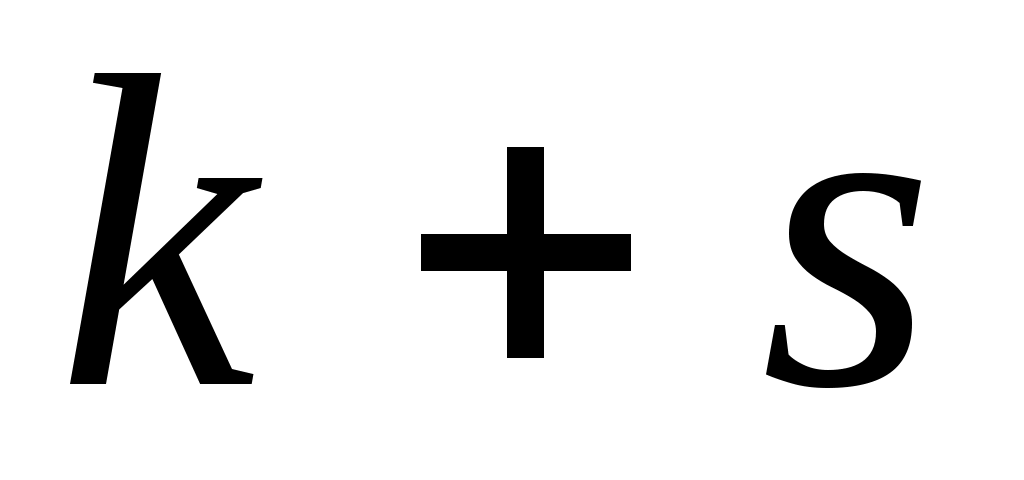 . Аналогічно, в базисі . Аналогічно, в базисі 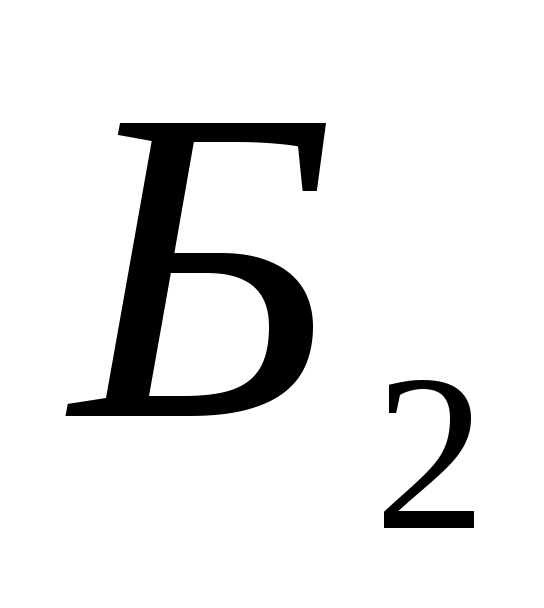 квадратичній функції квадратичній функції  відповідає діагональна матриця, ранг якої дорівнює відповідає діагональна матриця, ранг якої дорівнює 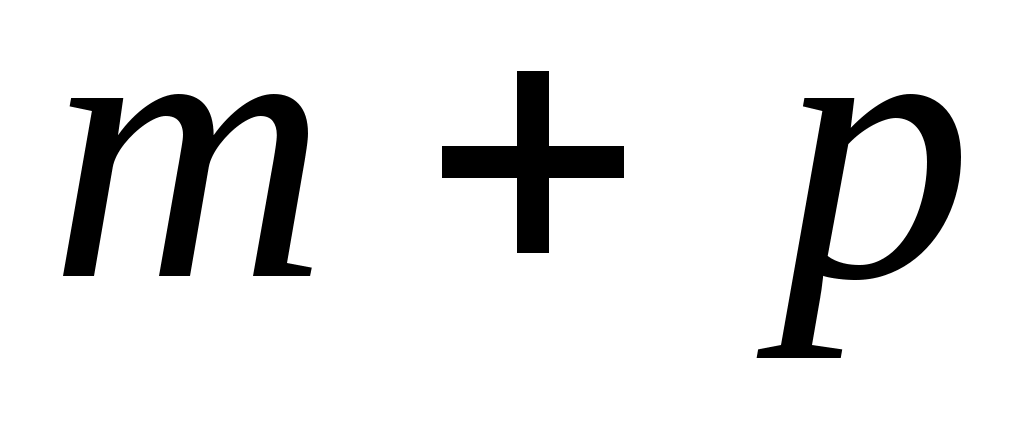 . Вище було показано, що ранг матриці білінійної функції не залежить від вибору базису, тому . Вище було показано, що ранг матриці білінійної функції не залежить від вибору базису, тому 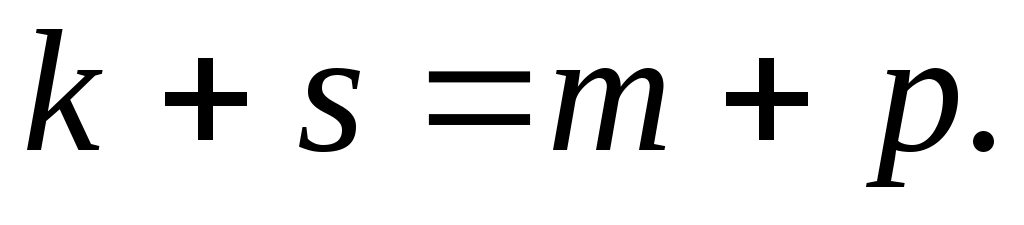
Покажемо тепер, що 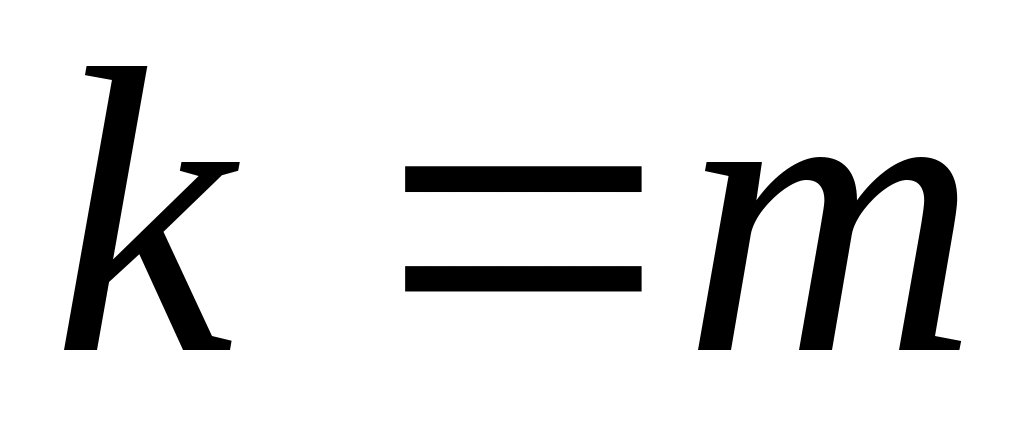 . Доведемо це від супротивного. Припустимо, що . Доведемо це від супротивного. Припустимо, що 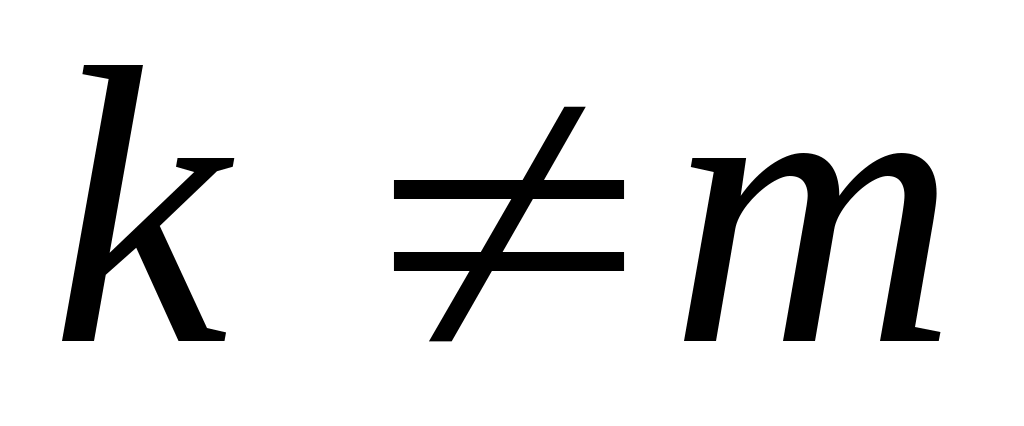 і, для визначеності, покладемо, що і, для визначеності, покладемо, що 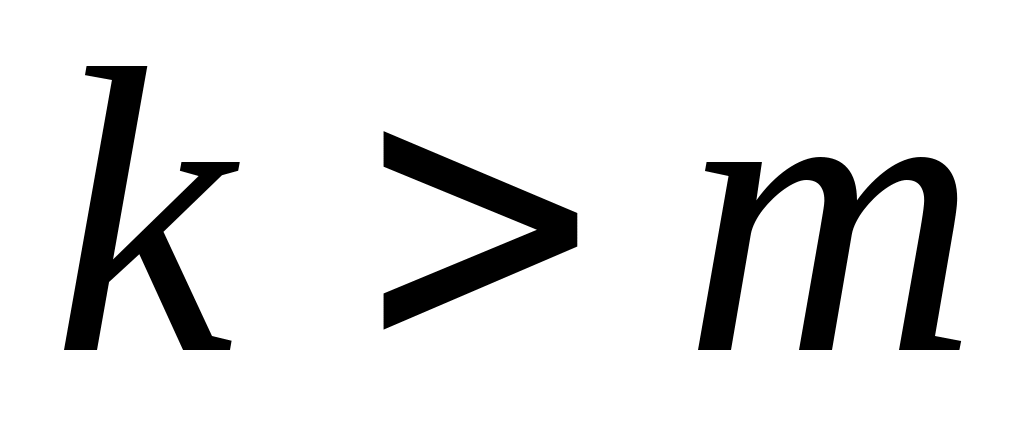 . Визначимо підпростори: . Визначимо підпростори:
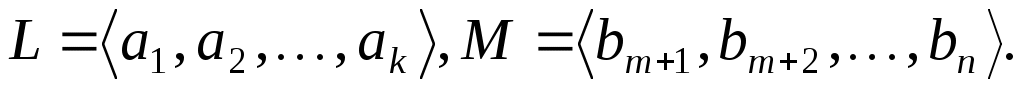
Тоді
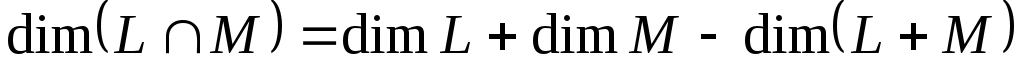 , ,
але
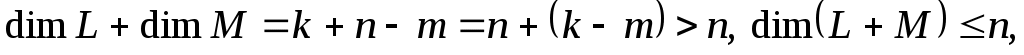
а тому
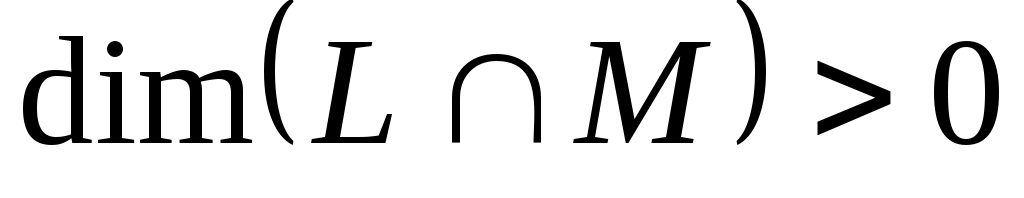 . .
Тобто, існує ненульовий вектор 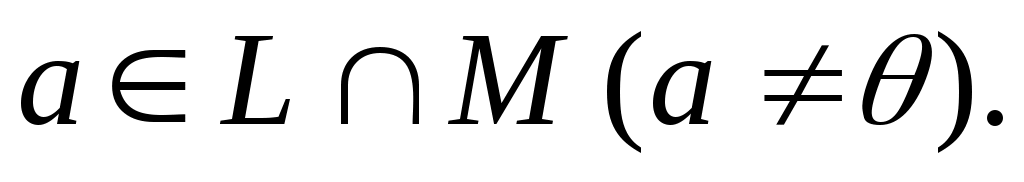
Оскільки 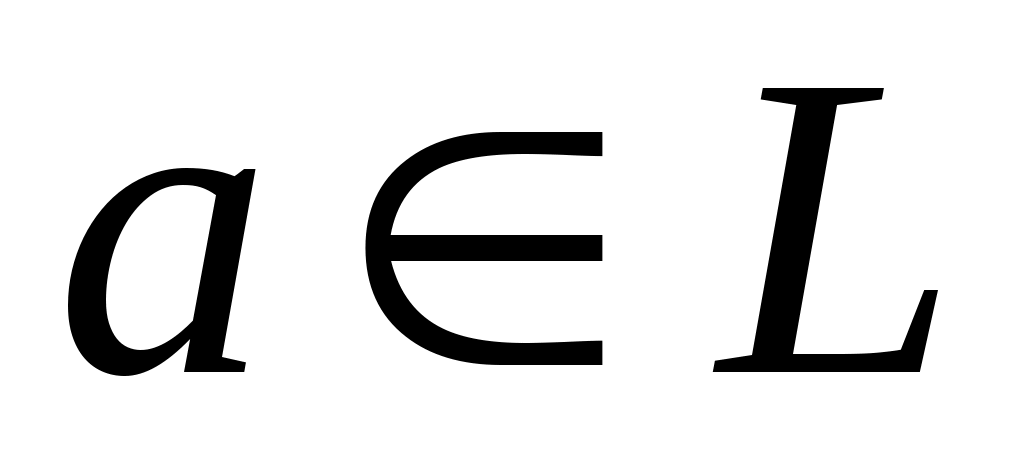 , то вектор , то вектор  лінійно виражається через вектори лінійно виражається через вектори 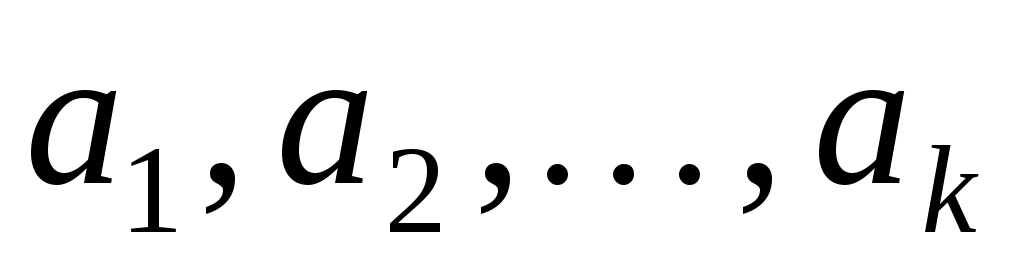 : :
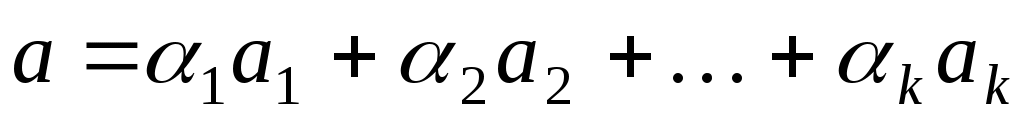 , ,
тобто, в базисі простору 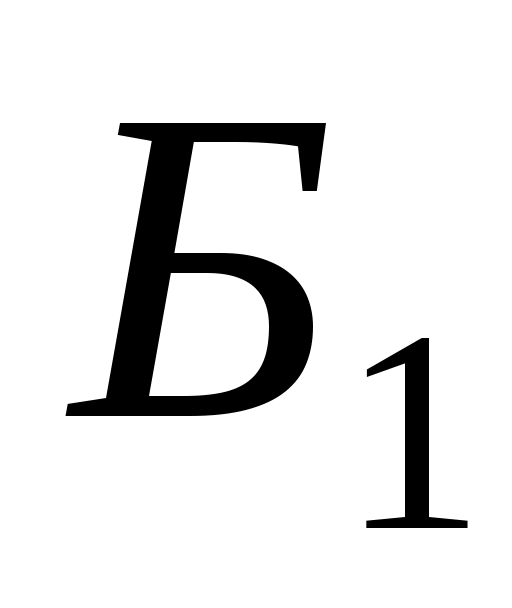 вектор вектор  задається такими координатами: задається такими координатами:
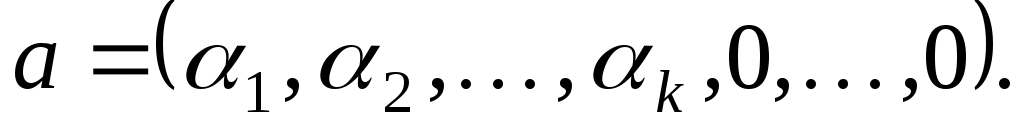
А тому
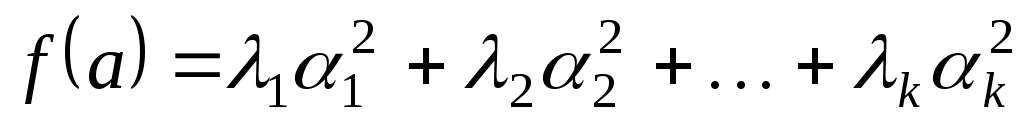 . .
Оскільки 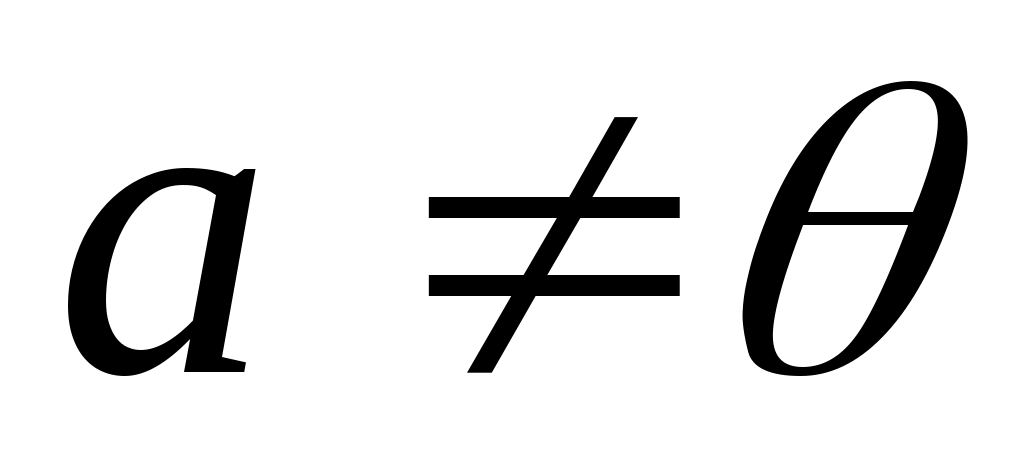 , то серед координат , то серед координат 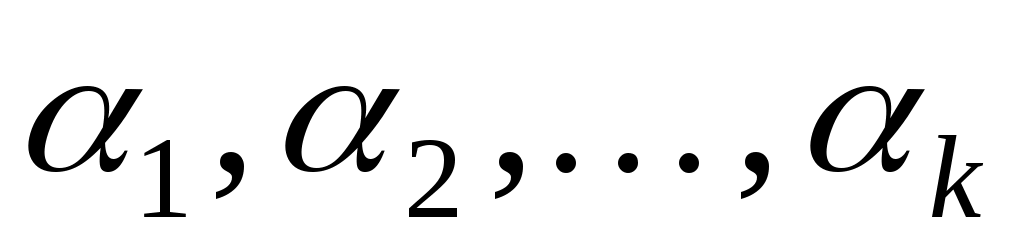 існує принаймні одна ненульова і, враховуючи, що існує принаймні одна ненульова і, враховуючи, що 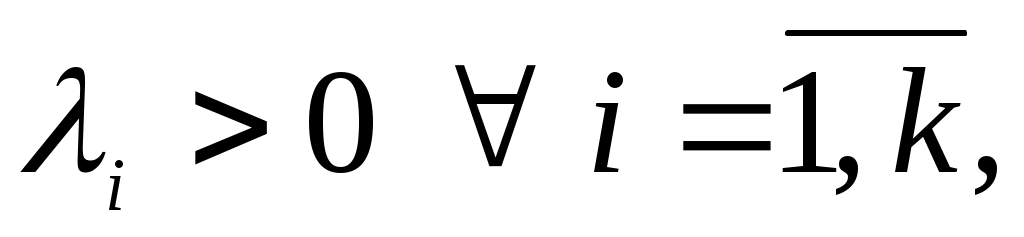 одержуємо, що одержуємо, що 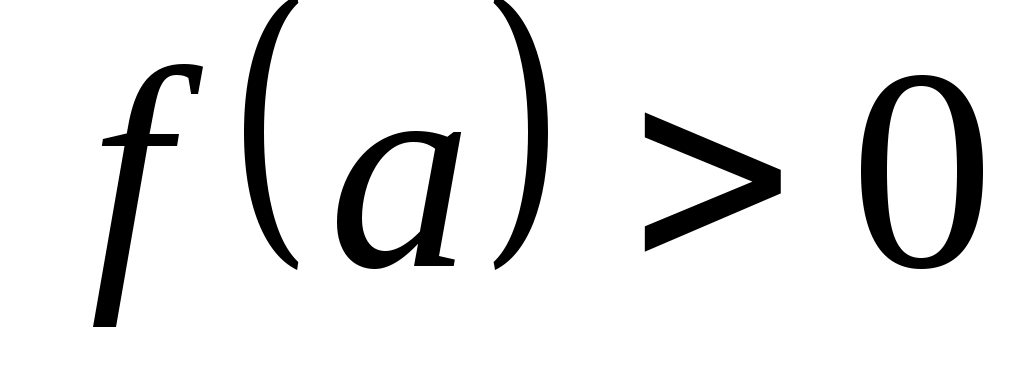 . Оскільки . Оскільки 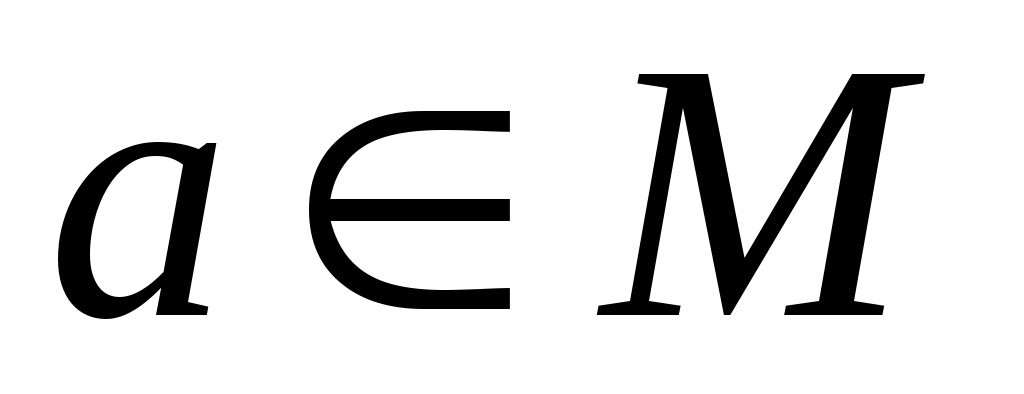 , то вектор , то вектор  лінійно виражається через вектори лінійно виражається через вектори 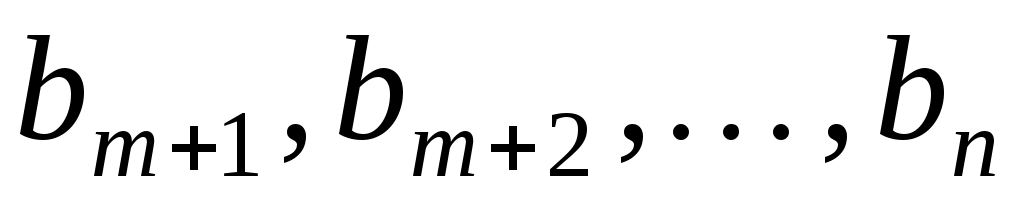 : :
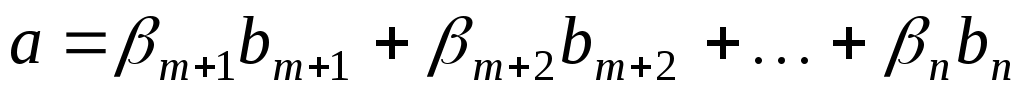 . .
Тобто, в базисі 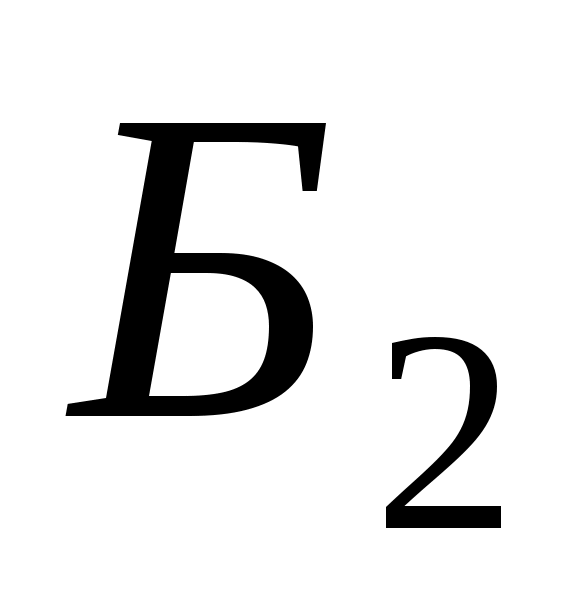 вектору вектору  відповідають такі координати: відповідають такі координати:
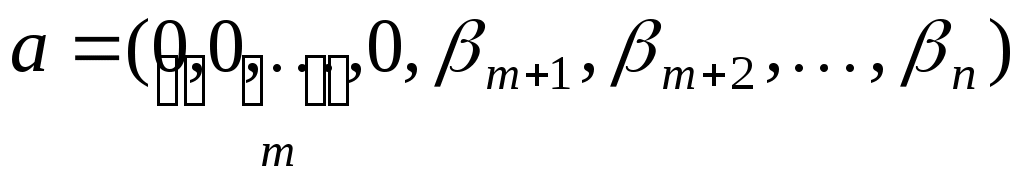 . .
Тоді
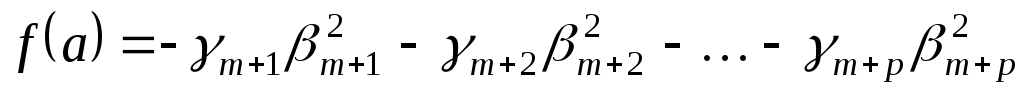 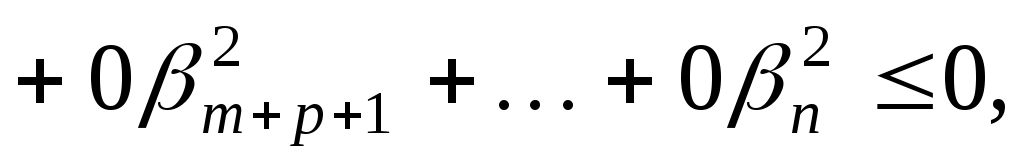
оскільки 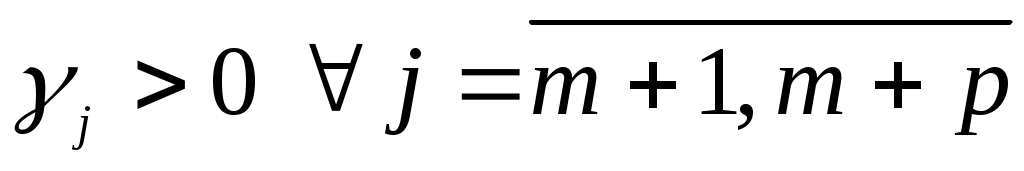 . Приходимо до суперечності: . Приходимо до суперечності:
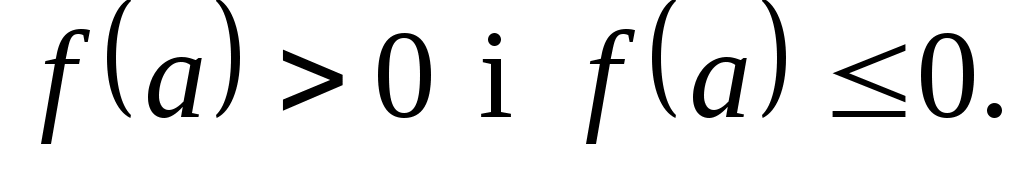
Отже, 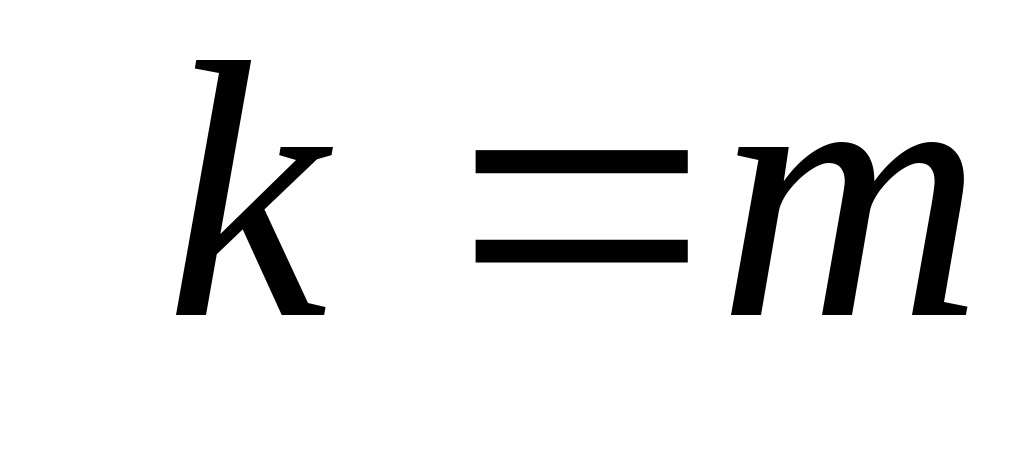 і, оскільки, за доведеним, і, оскільки, за доведеним, 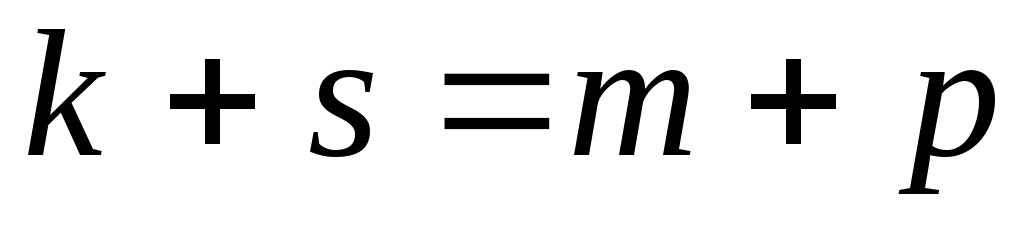 , то , то 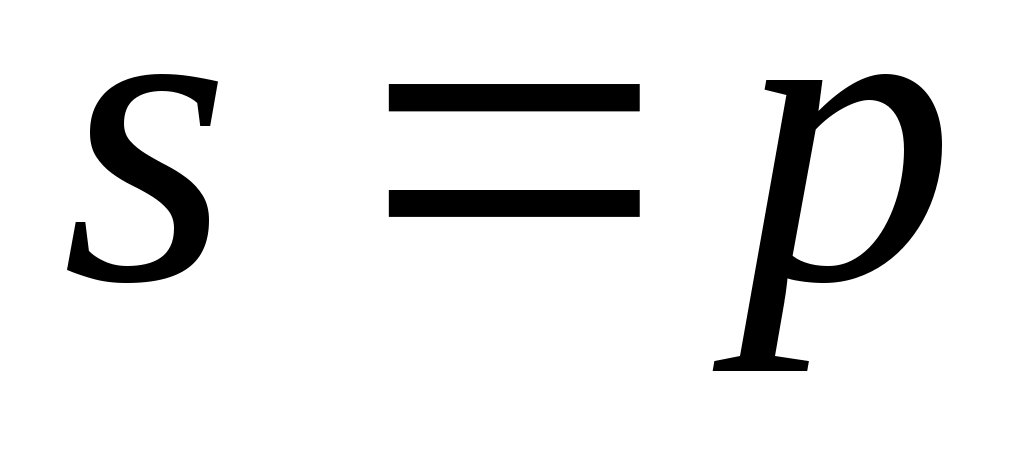 . .
Зауваження. Під рангом квадратичної функції розуміється ранг її полярної білінійної функції. Ранг білінійної функції дорівнює рангу її матриці в будь-якому базисі. Якщо квадратична функція зводиться до канонічного вигляду, то знаходиться базис, у якому квадратичній функції відповідає діагональна матриця і канонічна квадратична форма. На діагоналі матриці стоять коефіцієнти при квадратах змінних у квадратичній формі. Звідси випливає, що ранг квадратичної функції співпадає з числом ненульових коефіцієнтів у канонічній квадратичній формі, яка відповідає цій квадратичній функції.
|
|
|
 Скачать 1.43 Mb.
Скачать 1.43 Mb.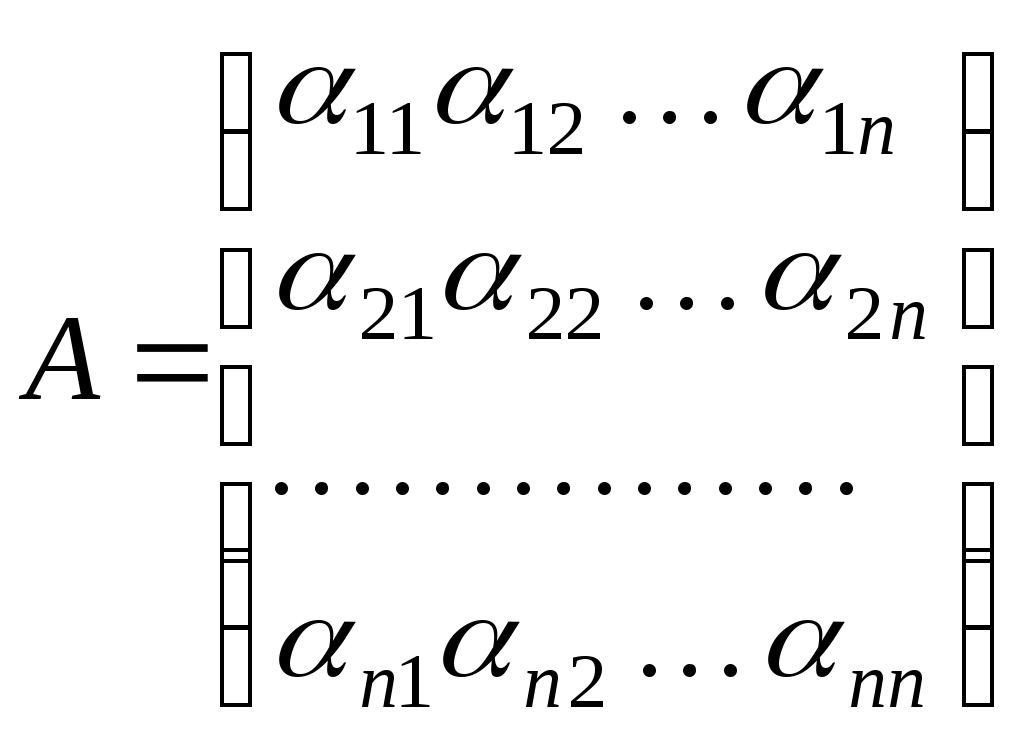 ,
,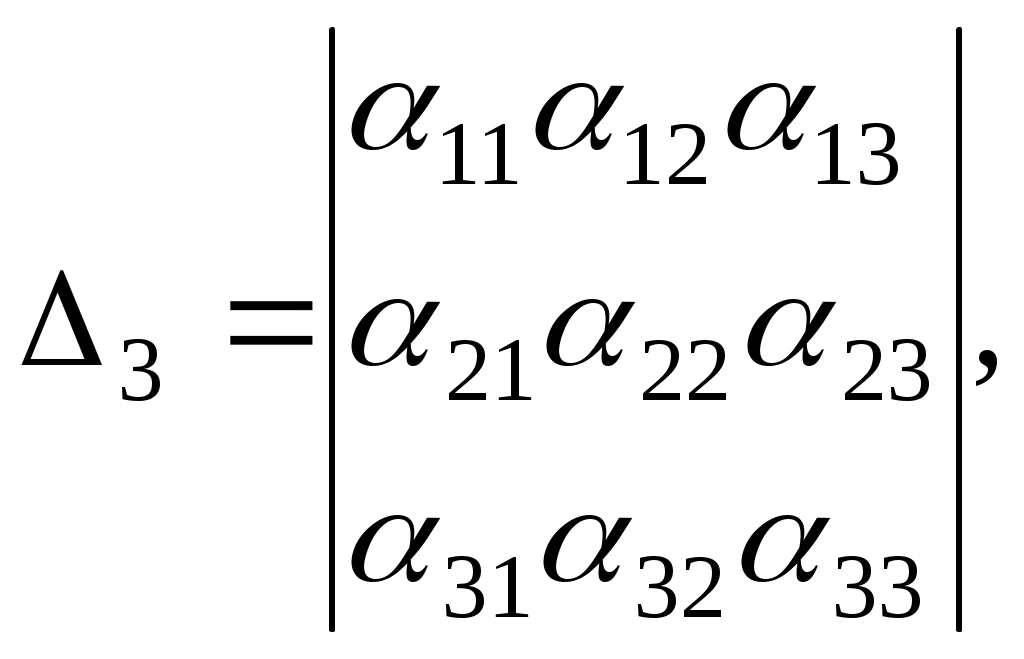
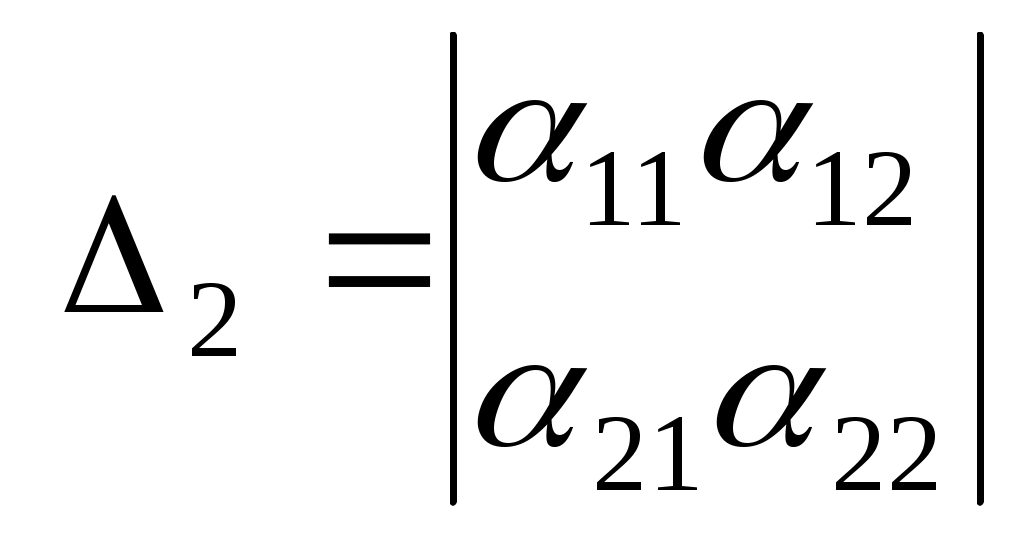 ,
, 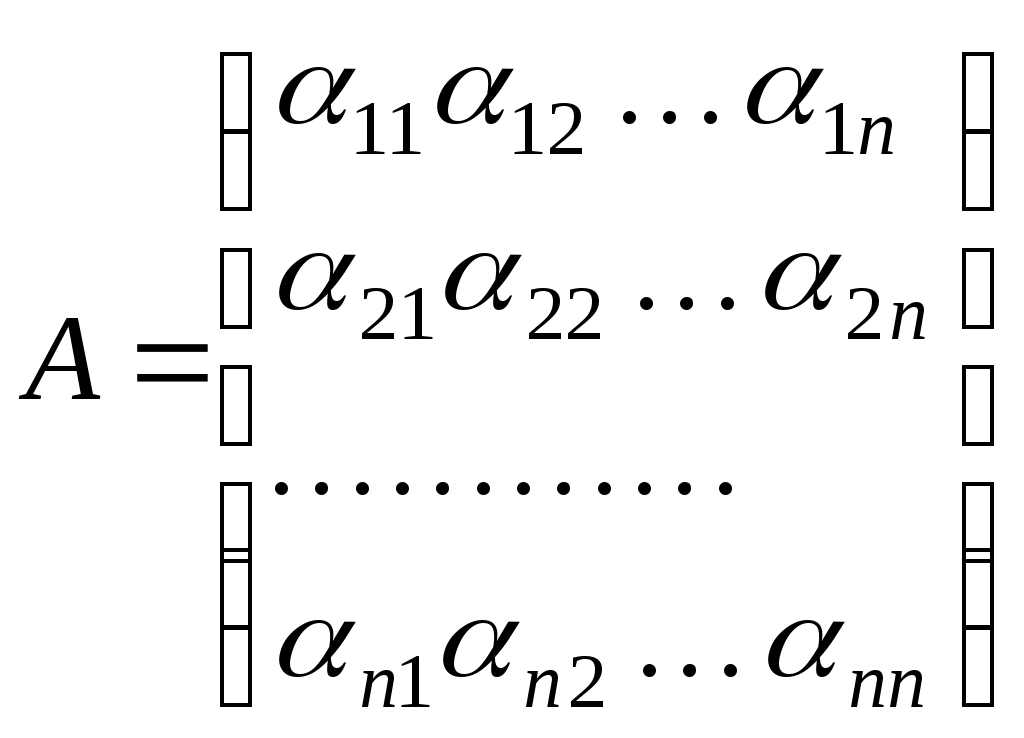 ,
,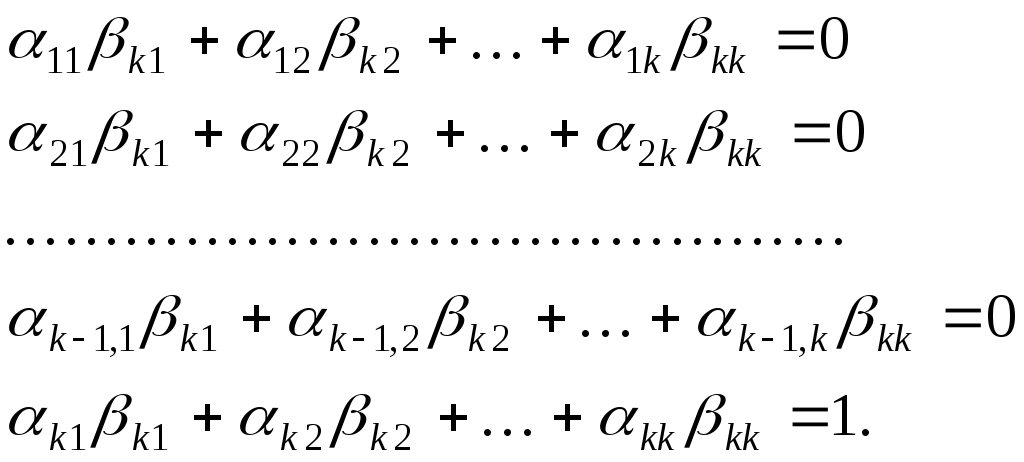
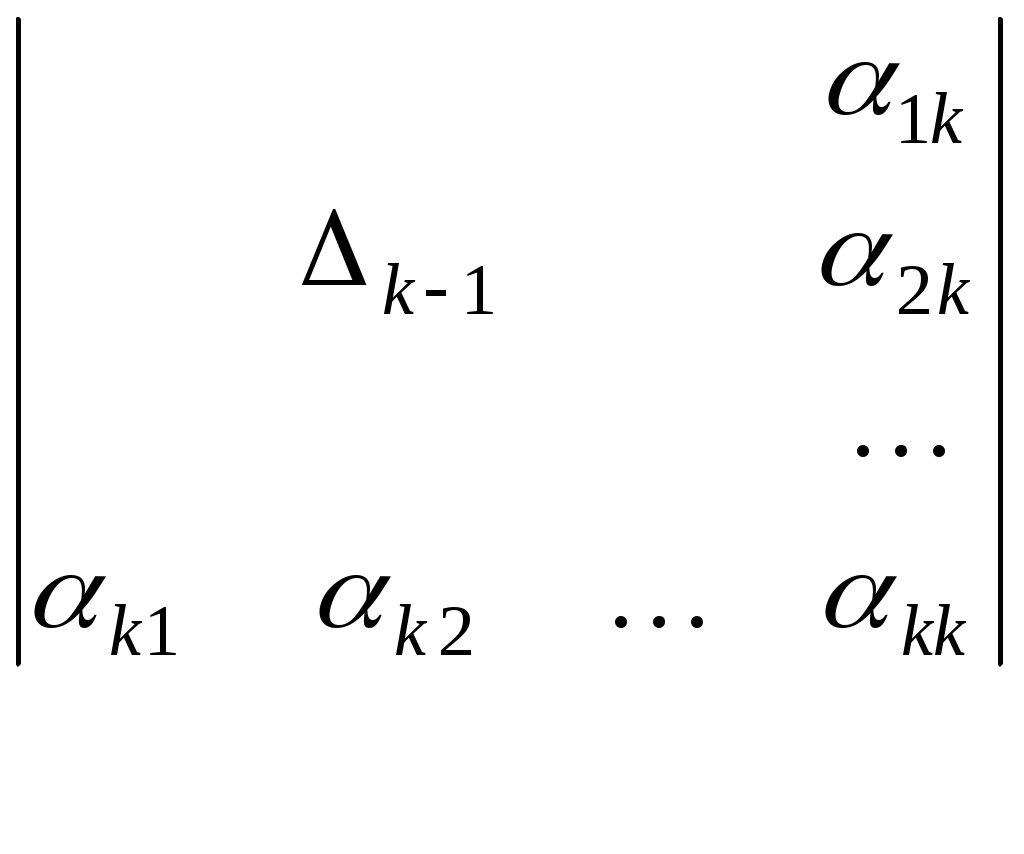 ,
,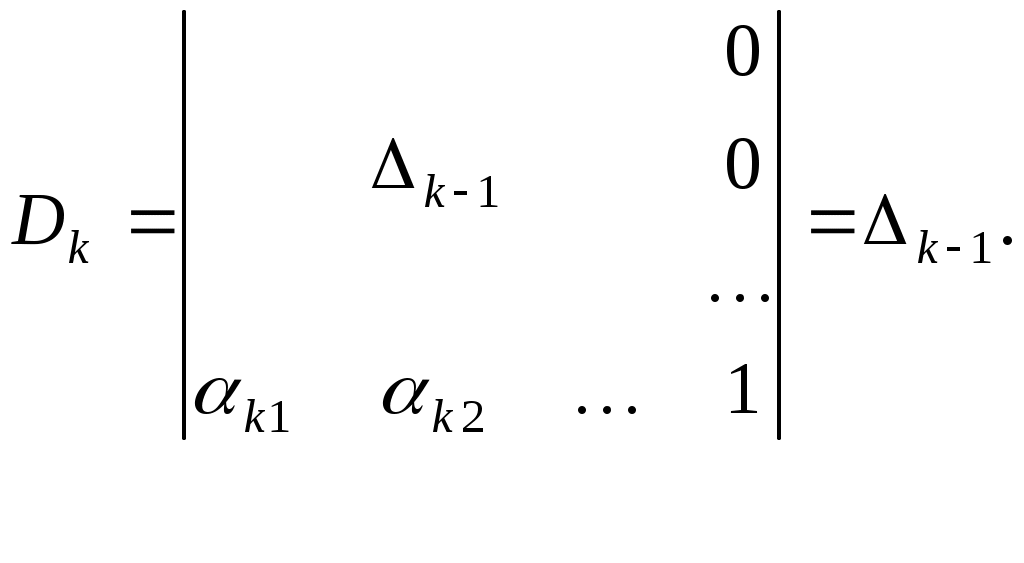
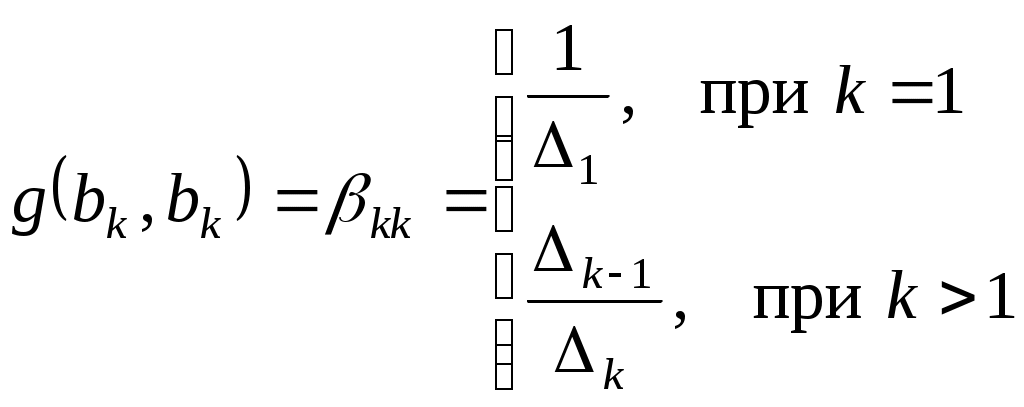 .
. .
.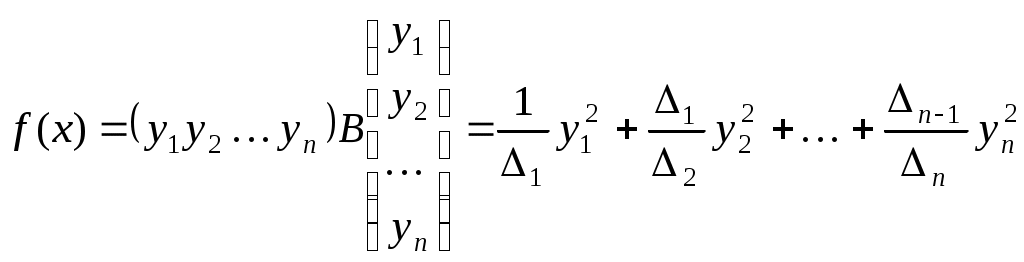 .
.