Билинейные формы Шестаков. Білінійні та квадратичні функції С. С. Шестаков. Конспект лекцій для студентів заочного відділенння
 Скачать 1.43 Mb.
|
|
Алгоритм зведення квадратичної функції до канонічного вигляду ортогональним перетворенням змінних Припустимо, що квадратична функція  у початковому базисі задається квадратичною формою від  змінних  .Складається матриця  квадратичної функції . Матриця симетрична.Знаходяться всі власні числа  матриці . Для матриці знаходиться ортонормований базис простору  , який складається з власних векторів матриці.Координати векторів  записуються в стовпчики матриці  . Ця матриця ортогональна і є матрицею переходу від початкового базису до базису .У базисі квадратична функція задається канонічною квадратичною формою:  Для початкових та заключних змінних виконується рівність:  .Класифікація поверхонь другого порядку Нехай  - простір усіх тривимірних векторів з дійсними координатами. В просторі зафіксовано деяку декартову прямокутну систему координат, якій відповідає ортонормований базис простору  . Вважаємо, що усі вектори простору задаються координатами в цьому базисі, тобто, якщо  то  Поверхнею другого порядку називається множина точок простору, координати яких задовольняють загальному рівнянню поверхні другого порядку:  де коефіцієнти  не дорівнюють нулю одночасно. Задача класифікації поверхонь другого порядкуполягає в тому, що визначається тип поверхні, яка задається даним рівнянням.Для розв’язання задачі знаходиться така декартова прямокутна система координат, у якій поверхня задається канонічним рівнянням. Як відомо, початок такої системи координат співпадає з центром поверхні, а вісі координат - з вісями поверхні. Позначимо:  .Ця сума є квадратичною формою від змінних  . Зводимо її до канонічного вигляду ортогональним перетворенням змінних. Це означає, що знайдеться такий ортонормований базис простору  , в якому квадратична форма має канонічний вигляд:  .Новому базису відповідає нова декартова прямокутна система координат. Якщо - матриця переходу від базису до базису , то для змінних виконується рівність  У рівнянні поверхні другого порядку зробимо заміну змінних за цією формулою. В новій системі координат поверхня задається рівнянням:  .Ортогональне перетворення змінних означає, що зроблено поворот системи координат на деякий кут у деякій площині. Далі аналіз розбивається на три випадки, в залежності від числа квадратів, що залишились: 1. Залишилось три квадрати. 2. Залишилось два квадрати. 3. Залишився один квадрат. Розглянемо випадок 1. Залишається три квадрати, тобто 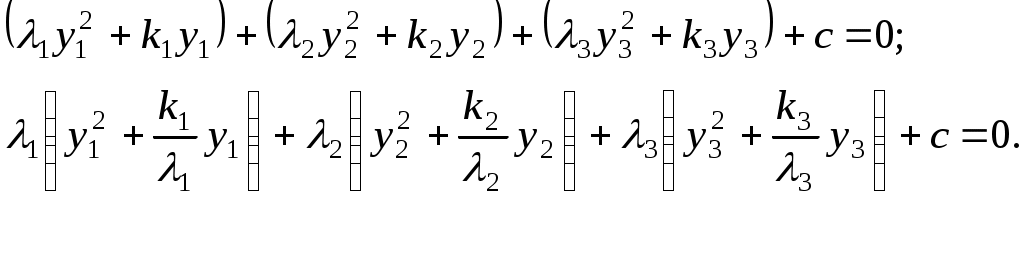 . Перепишемо рівняння у вигляді:  Виділяємо повні квадрати: 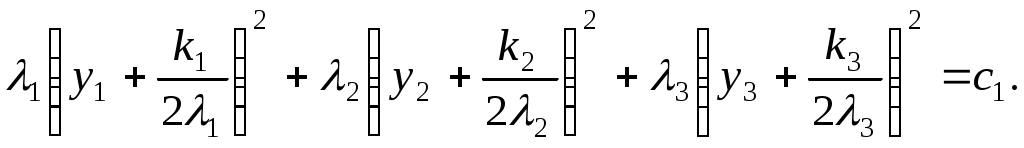 Зробимо заміну змінних:  .Ця заміна означає, що виконується паралельне перенесення системи координат  таким чином, що початок координат переноситься в точку з координатами: У новій системі координат поверхня задається рівнянням  .Далі можливі такі варіанти: 1) Числа 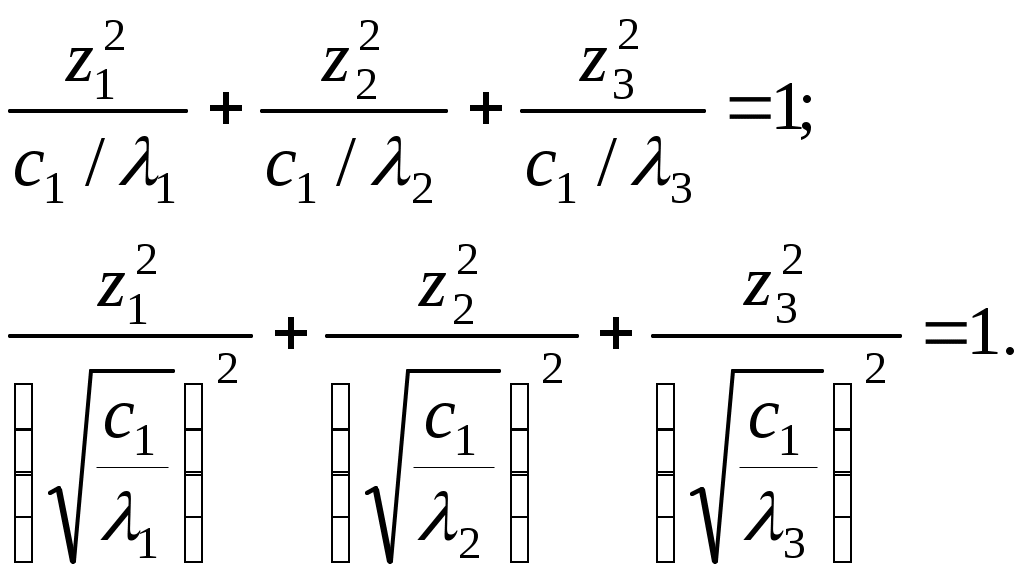 одного знаку. Можна вважати, що  . Тоді:а) Якщо  , то рівняння перепишеться у вигляді:  Одержується рівняння еліпсоїда. б) Якщо  , то рівняння розв’язків не має, тобто, задає порожню множину.в) Якщо  , то рівняння задає єдину точку з координатами:  2) Якщо знаки чисел різні, то можна вважати, що  . Тоді: а) Якщо 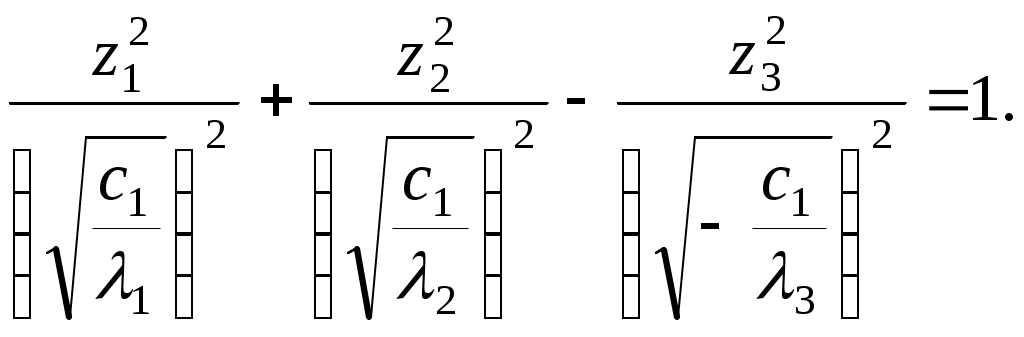, то перепишемо рівняння у вигляді:  Одержується рівняння однопорожненого гіперболоїда. б) Якщо 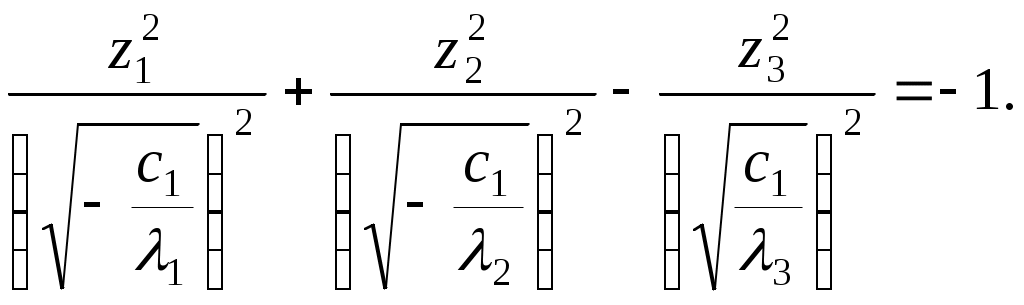, то перепишемо рівняння у вигляді:  Одержується рівняння двопорожненого гіперболоїда. в) Якщо 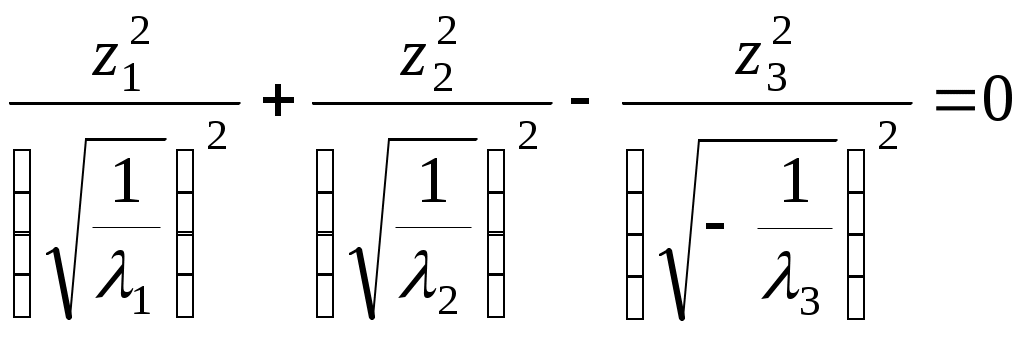, то перепишемо рівняння у вигляді: .Одержується рівняння конуса. Розглянемо випадок 2. Залишається два квадрати. Припустимо, що 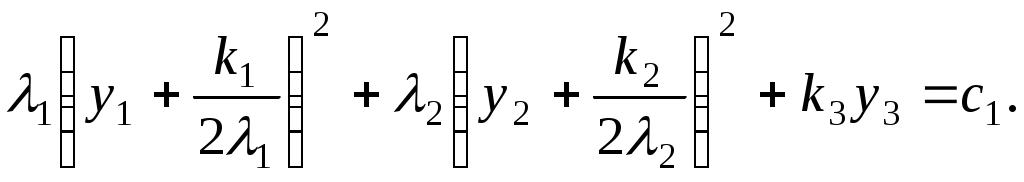 . Перепишемо рівняння у вигляді:  1) Припустимо спочатку, що  . Зробимо заміну змінних:  Заміна означає, що виконується паралельне перенесення системи координат таким чином, що початок координат переноситься в точку з координатами: У новій системі координат поверхня задається таким рівнянням:  Припустимо спочатку, що числа 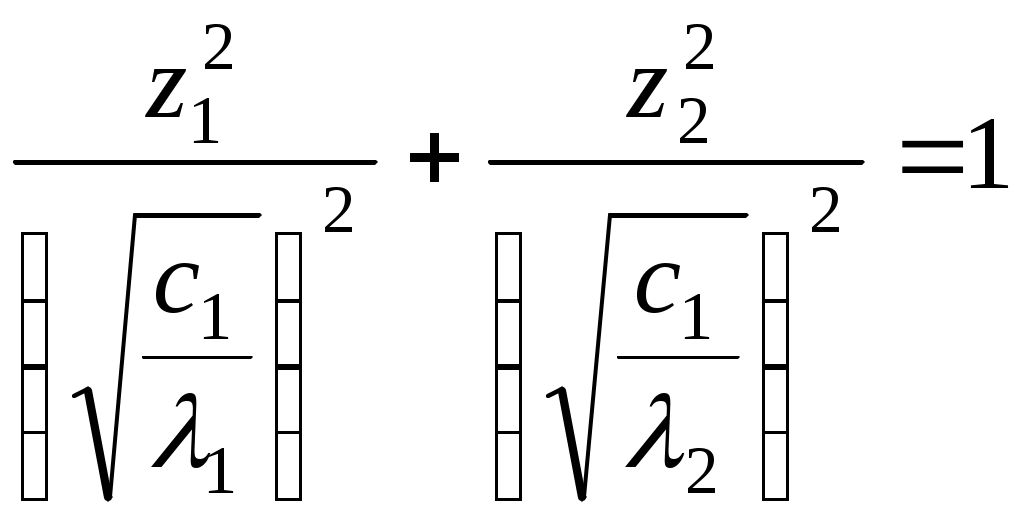 одного знаку. Можна вважати, що  .Тоді:а) Якщо , то переписуємо рівняння у вигляді: .Одержуємо рівняння еліптичного циліндра. б) Якщо  то рівняння розв’язків не має, тобто задає порожню множину.в) Якщо , то  Система двох рівностей задає пряму – вісь координат  .Припустимо тепер, що знаки чисел 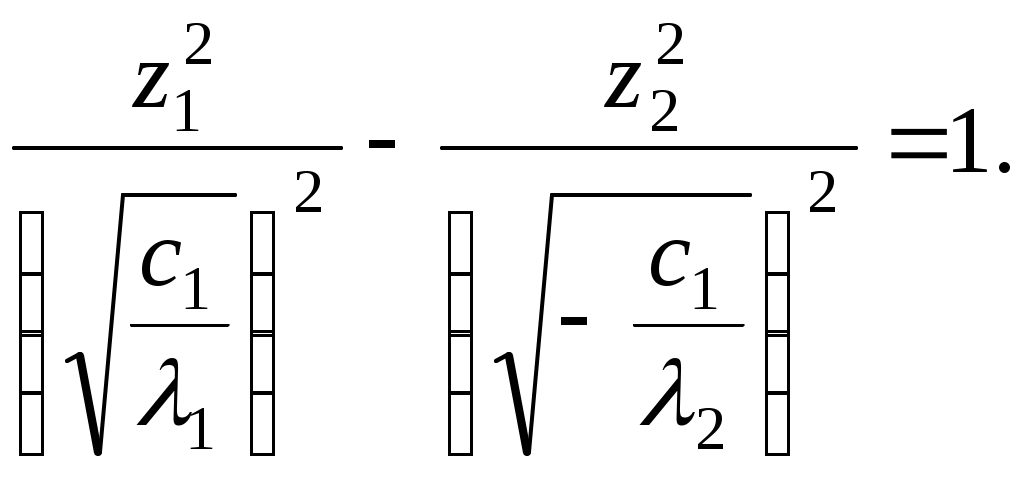 протилежні. Можна вважати, що  . Тоді:а) Якщо  , то можна вважати, що  Рівняння перепишемо у вигляді: Одержується рівняння гіперболічного циліндра. б) Якщо , то одержуємо рівняння .Таке рівняння задає пару площин . 2) Припустимо тепер, що 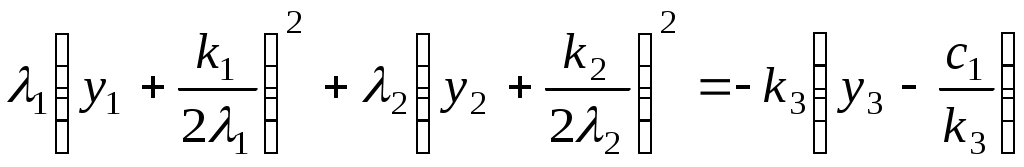 . Перепишемо рівняння у вигляді:  .Зробимо заміну змінних:  Заміна означає, що виконується паралельне перенесення системи координат таким чином, що початок координат переноситься в точку з координатами: У новій системі координат поверхня задається таким рівнянням:  .Можливі такі варіанти: а) Якщо числа 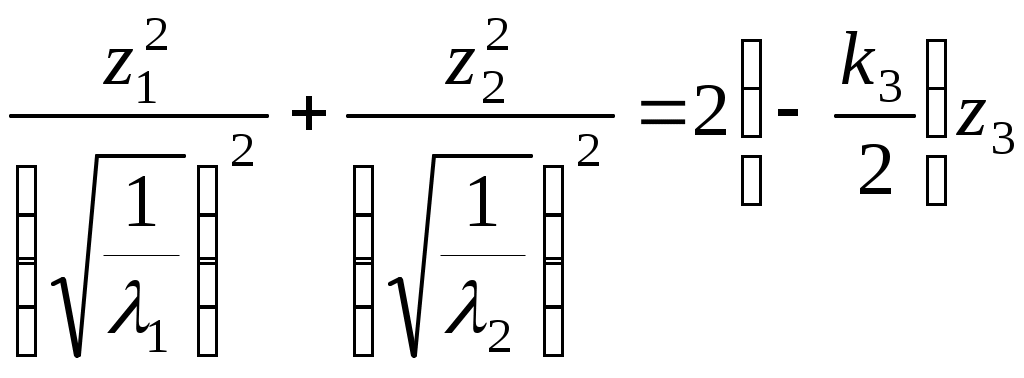 одного знаку, то можна вважати, що . Перепишемо рівняння у вигляді: .Одержується рівняння еліптичного параболоїда. б) Якщо знаки чисел 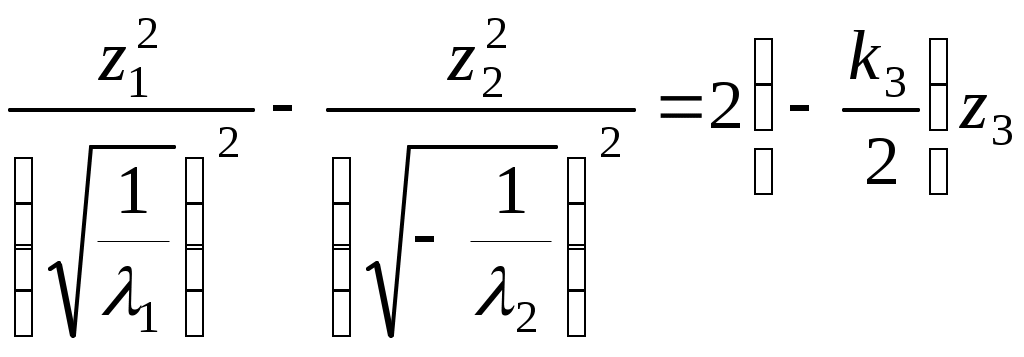протилежні, то вважаємо  і одержуємо рівняння:  .Одержуємо рівняння гіперболічного параболоїда. Розглянемо випадок 3. Залишається один квадрат. Вважаємо, що 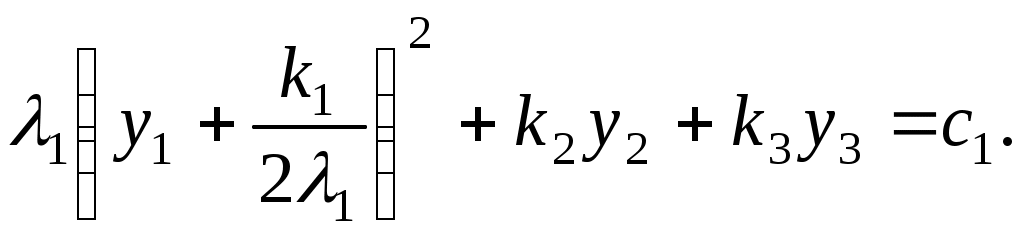 . Перепишемо рівняння у вигляді: Далі можливі три варіанти, в залежності від наявності змінних  .Нехай  Зробимо заміну змінних:  .Заміна означає, що виконується паралельне перенесення системи координат таким чином, що початок координат переноситься в точку з координатами: У новій системі координат поверхня задається таким рівнянням:  .Вважаємо, що  . Тоді: а) Якщо , то рівняння перепишемо у вигляді: .Рівняння задає пару площин. б) Якщо , рівняння розв’язків не має, тобто задає порожню множину.в) Якщо  то рівняння можна переписати у вигляді: .Одержуємо рівняння одної площини. Нехай 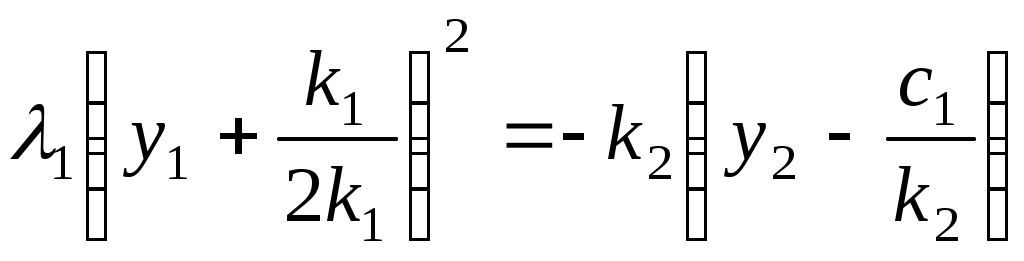 , . Перепишемо рівняння таким чином:  .Зробимо заміну змінних:  Заміна означає, що виконується паралельне перенесення системи координат таким чином, що початок координат переноситься в точку з координатами: У новій системі координат поверхня задається таким рівнянням:  ,або   .Одержується рівняння параболічного циліндра. Нехай  . Зробимо заміну змінних:  Така заміна означає поворот системи координат у деякій площині на деякий кут. У новій системі координат одержується рівняння типу, який розглядається в попередньому випадку. Література КУРОШ А.Г. Курс высшей алгебры. – М.: Наука, 1965. - 360 с. ПРОСКУРЯКОВ И.В. Сборник задач по линейной алгебре.- М.: Наука, 1984.- 380 с. 3. ФАДДЕЕВ Д.К., СОМИНСКИЙ И.С. Сборник задач по высшей алгебре. – М.: Наука, 1977. - 302 с. Предметний вказівник
|