Конспект лекций по компьютерной графике. Конспект лекций по дисциплине Компьютерная графика
 Скачать 16.3 Mb. Скачать 16.3 Mb.
|
3.4. Базовые растровые алгоритмыАлгоритмы вывода прямой линииРассмотрим растровые алгоритмы для отрезков прямой линии. Предположим, что заданы координаты ( x1, yl - х2, у2) концов отрезка прямой. Для вывода линии необходимо закрасить определенным цветом все пикселы вдоль линии. Для того чтобы закрасить любой пиксел, необходимо знать его координаты. Наиболее просто нарисовать отрезок горизонтальной линии. Вычисление текущих координат пиксела выполняется как приращение по x(необходимо, чтобы х1 ≤ х2), а вывод пиксела обеспечивается специальной функцией. Аналогично рисуется отрезок вертикали. В цикле вывода горизонтального и вертикального отрезков выполняются простейшие операции — приращение на единицу, проверка на "< =" и запись пиксела в буфер растра. Поэтому операция рисования таких отрезков выполняется быстро и просто. Ее используют как базовую операцию для других операций, например, в алгоритмах заполнения полигонов. Можно задать такой вопрос: какая линия рисуется быстрее — горизонталь или вертикаль? На первый взгляд — одинаково быстро. Если учитывать только математические аспекты, то скорость должна быть одинаковой при равной длине отрезков линий, поскольку в обоих случаях выполняется одно и то же количество одинаковых операций. Однако если кроме вычисления координат анализировать вывод пикселов в конкретный растр, то могут быть отличия. В растровых системах рисование пиксела обычно означает запись одного или нескольких битов в память, где сохраняется растр. И здесь уже не все равно — по строкам или по столбцам заполняется растр. Необходимо учитывать логическую организацию памяти компьютера, в которой хранятся биты или байты растра. Даже для компьютеров одного типа (например, персональных компьютеров) для разных поколений процессоров и памяти скорость записи по соседним адресам может существенно отличаться от скорости записи по не соседним адресам. В особенности это заметно, если для растра используется виртуальная память с сохранением отдельных страниц на диске и (или) в оперативной памяти (RAM). При работе графических программ в среде операционной системы Windows часто случается так, что горизонтали рисуются быстрее вертикалей, так как в каждой странице памяти сохраняются соседние байты — пикселы вдоль горизонтали растра. Подобный эффект также имеет место при использовании кэш-памяти. А может быть, что RAM достаточно, и даже весь растр размещается в кэше, а скорости рисования все же отличаются. Например, если используется черно-белый растр в формате один бит на пиксел, то для вертикали битовая маска одинакова для всех пикселов линии, а для горизонтали маску нужно изменять на каждом шаге. Здесь необходимо заметить, что рисование черно-белых горизонталей можно существенно ускорить, если записывать сразу восемь соседних пикселов — байт в памяти. Горизонтали и вертикали представляют собой частный случай линий. Рассмотрим линию общего вида. Для нее также необходимо вычислять координаты любого пиксела. Известны несколько методов расчетов координат точек линии. Прямое вычисление координат Пусть заданы координаты конечных точек отрезка прямой. Найдем координаты точки внутри отрезка. Запишем соотношения катетов для подобных прямоугольных треугольников: Перепишем это соотношение как х =f(y): а также как В зависимости от угла наклона прямой выполняется цикл по оси х или по у(рис. 3. 28). Рис. 3.28. Отрезок прямой. 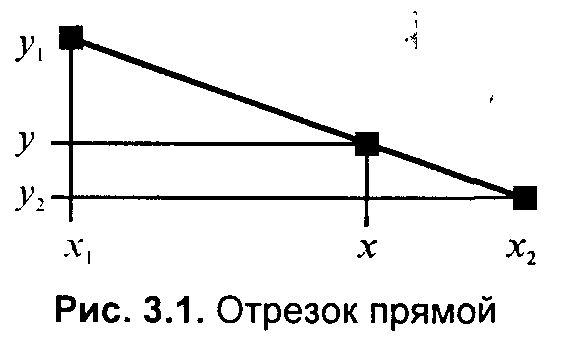 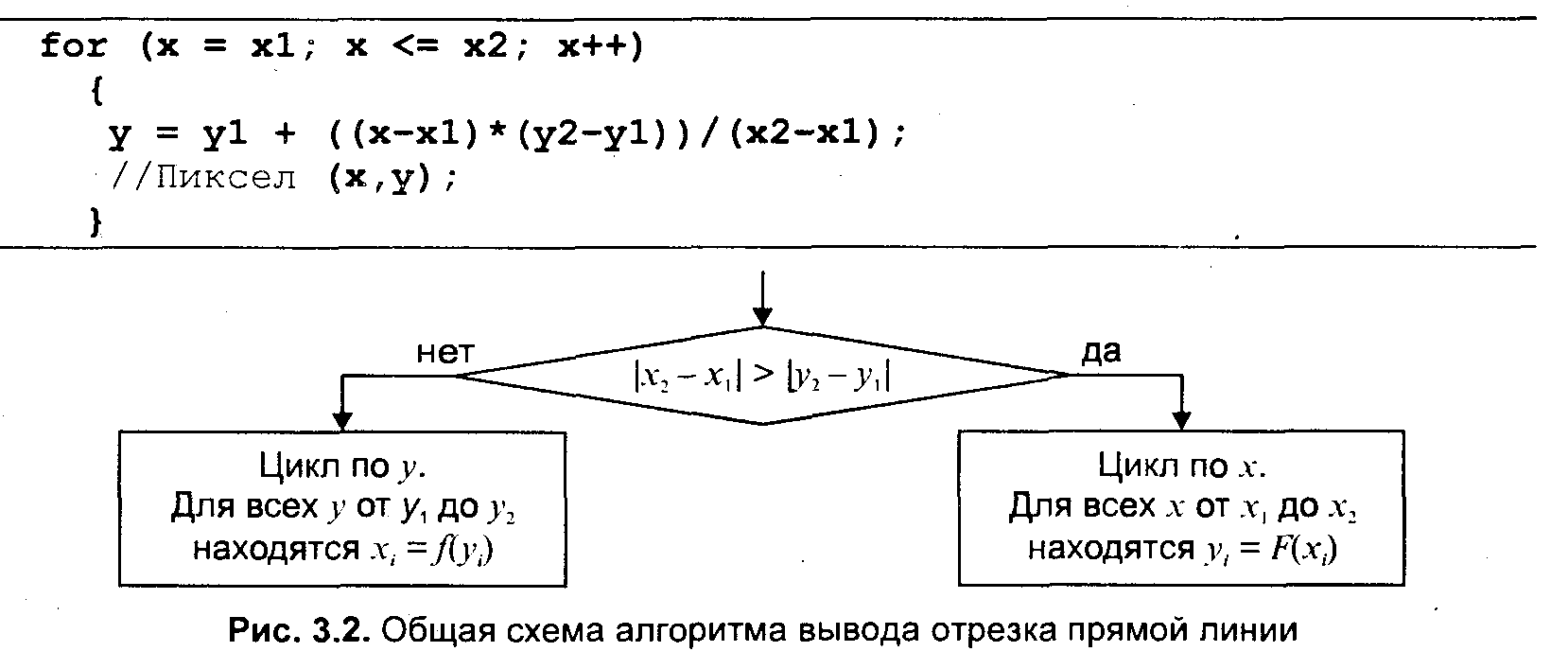 Рис. 3.29. Общая схема алгоритма вывода отрезка прямой линии Положительные черты прямого вычисления координат. 1. Простота, ясность построения алгоритма. 2. Возможность работы с нецелыми значениями координат отрезка. (Как вы считаете, в каком варианте из четырех корректно вычисляются координаты пикселов, если х1, у1, х2 и у2 — дробные?) Недостатки. 1. Использование операций с плавающей точкой или целочисленных операций умножения и деления обуславливает маленькую скорость. Однако это зависит от процессора, и для разных типов компьютеров может быть по-разному. В современных компьютерах, в которых процессоры используют эффективные средства ускорения (например, конвейер арифметических операций с плавающей точкой), время выполнения целочисленных операций уже не намного меньше. Для старых компьютеров разница могла составлять десятки раз, поэтому и старались разрабатывать алгоритмы только на основе целочисленных операций. 2. При вычислении координат добавлением приращений может накапливаться ошибка вычислений координат. Последнюю разновидность прямого вычисления координат, рассмотренную здесь, можно было бы назвать "инкрементной". Но такое название получили алгоритмы другого типа. Инкрементные алгоритмыБрезенхэм предложил подход, позволяющий разрабатывать так называемые инкрементные алгоритмы растеризации. Основной целью при разработке таких алгоритмов было построение циклов вычисления координат на основе только целочисленных операций сложения/вычитания без использования умножения и деления. Были разработаны инкрементные алгоритмы не только для прямых, но и для кривых линий. Инкрементные алгоритмы выполняются как последовательное вычисление координат соседних пикселов путем добавления приращений координат. Приращения рассчитываются на основе анализа функции погрешности. В цикле выполняются только целочисленные операции сравнения и сложения/вычитания. Достигается повышение быстродействия для вычислений каждого пиксела по сравнению с прямым способом. Рассмотрим пример работы приведенного выше алгоритма Брезенхэма для отрезка (х1у1 - х2у2) = (2, 3 - 8, 6). Этот алгоритм восьмисвязный, то есть при выполнении приращений координат для перехода к соседнему пикселу возможны восемь случаев (рис. 3. 30). 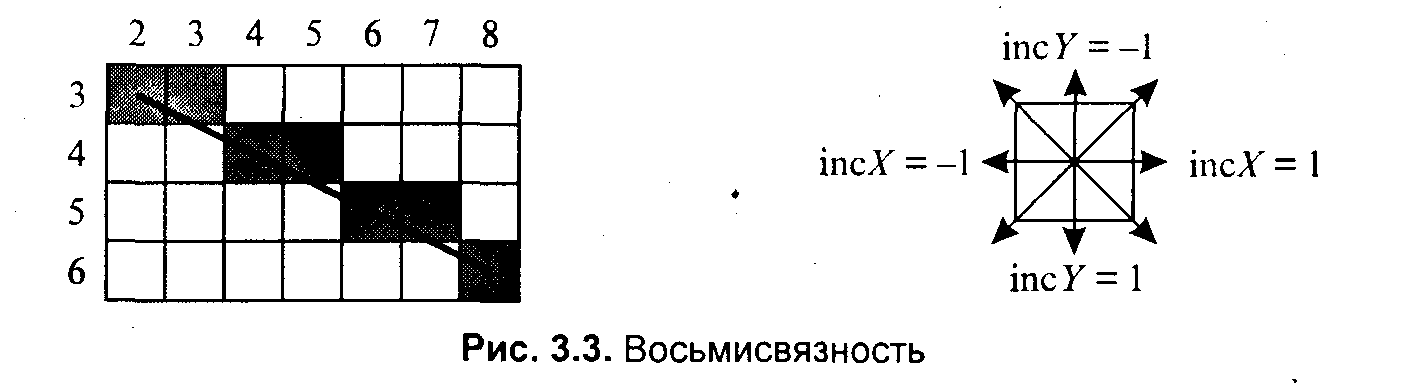 Рис. 3.30. Восьмисвязность Известны также четырехсвязные алгоритмы (рис. 3. 31). 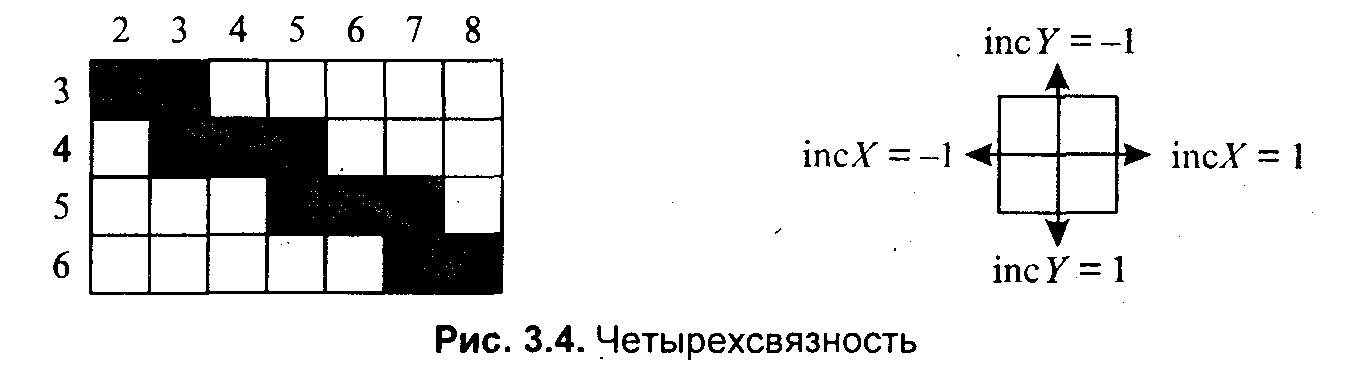 Рис. 3.31. Четырехсвязность Четырехсвязные алгоритмы проще, но они генерируют менее качественное изображение линий за большее количество тактов работы. Для приведенного примера четырехсвязный алгоритм работает 10 тактов, а восьмисвязный — только 7. Кривая БезьеРазработана математиком Пьером Безье. Кривые и поверхности Безье были использованы в 60-х годах компанией "Рено" для компьютерного проектирования формы кузовов автомобилей. В настоящее время они широко используются в компьютерной графике. Кривые Безье описываются в параметрической форме: Значение tвыступает как параметр, которому соответствуют координаты отдельной точки линии. Параметрическая форма описания может быть удобнее для некоторых кривых, чем задание в виде функции у =ƒ(х), поскольку функция ƒ(х) может быть намного сложнее, чем Px(t) и Py(t), кроме того, ƒ(x) может быть неоднозначной. Многочлены Безье для Рx и Рy имеют такой вид: 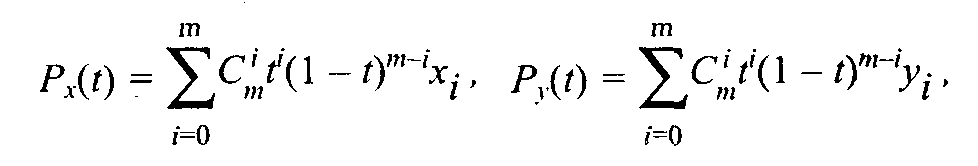 где xi и yi— координаты точек-ориентиров Рi, а величины — это известные из комбинаторики, так называемые сочетания (они также известны как коэффициенты бинома Ньютона): Значение да можно рассматривать и как степень полинома, и как значение, которое на единицу меньше количества точек-ориентиров. Рассмотрим кривые Безье, классифицируя их по значениям т. т = 1(по двум точкам) Кривая вырождается в отрезок прямой линии, которая определяется конечными точками Ро и Р1, как показано на рис. 3. 30: m=2 (по трем точкам, рис. 3. 32): 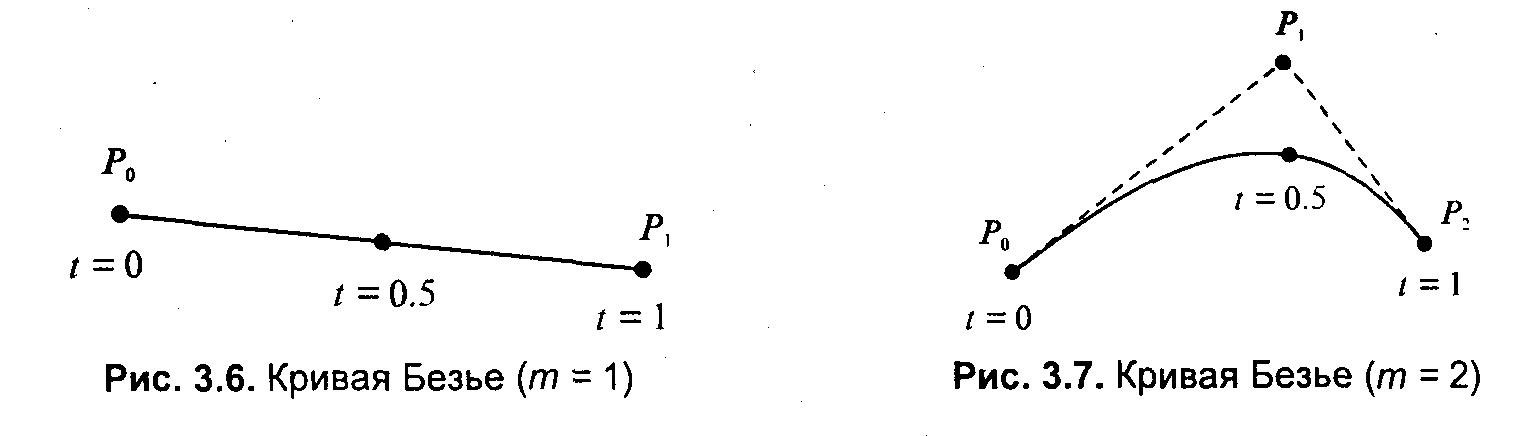 Рис. 3.32. Кривая Безье (m=1) Кривая Безье (m=2) т = 3 (по четырем точкам, кубическая, рис 3.33). Используется довольно часто, в особенности в сплайновых кривых: 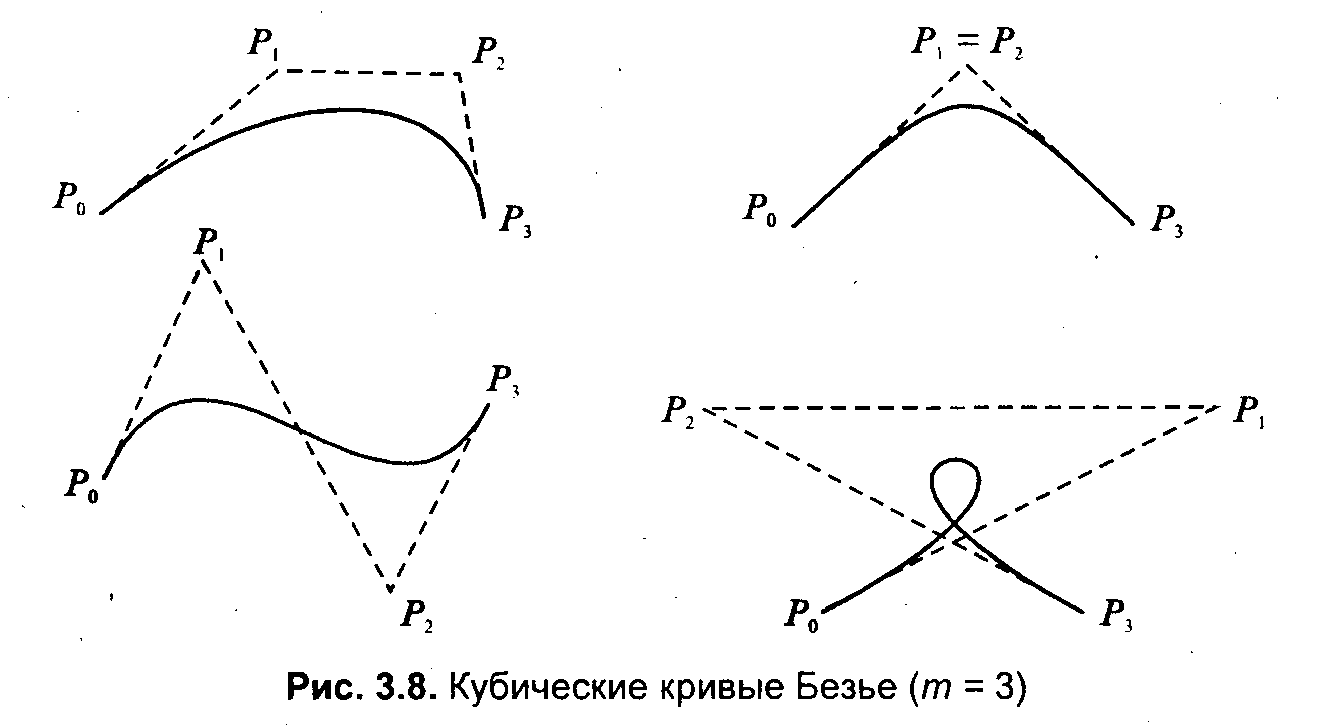 Рис. 3.33. Кубические кривые Безье (m=3) Геометрический алгоритм для кривой Безье Этот алгоритм позволяет вычислить координаты (х, у) точки кривой Безье по значению параметра t. 1. Каждая сторона контура многоугольника, который проходит по точкам-ориентирам, делится пропорционально значению t. 2.Точки деления соединяются отрезками прямых и образуют новый многоугольник. Количество узлов нового контура на единицу меньше, чем количество узлов предшествующего контура. 3. Стороны нового контура снова делятся пропорционально значению t. И так далее. Это продолжается до тех пор, пока не будет получена единственная точка деления. Эта точка и будет точкой кривой Безье (рис. 3.34).  Рис. 3.34. Геометрический алгоритм для кривых Безье Алгоритмы вывода фигурФигурой здесь будем считать плоский геометрический объект, который состоит из линий контура и точек заполнения, которые помещаются внутри контура. Контуров может быть несколько — например, если объект имеет внутри пустоты (рис. 3.35). В некоторых графических системах одним объектом может считаться и более сложная многоконтурная фигура - совокупность островов с пустотами. Графический вывод фигур делится на две задачи: вывод контура и вывод точек заполнения. Поскольку контур представляет собой линию, то вывод контура проводится на основе алгоритмов вывода линий. В зависимости от сложности контура, это могут быть отрезки прямых, кривых или произвольная последовательность соседних пикселов.  Рис. 3.35. Пример фигуры Для вывода точек заполнения известны методы, которые разделяются в зависимости от использования контура на два типа: алгоритмы закрашивания от внутренней точки к границам произвольного контура и алгоритмы, которые используют математическое описание контура. Алгоритмы закрашиванияРассмотрим алгоритмы закрашивания произвольного контура, который уже нарисован в растре. Сначала определяются координаты произвольного пиксела, находящегося внутри очерченного контура фигуры. Цвет этого пиксела изменяем на нужный цвет заполнения. Потом проводится анализ цветов всех соседних пикселов. Если цвет некоторого соседнего пиксела не равен цвету границы контура или цвету заполнения, то цвет этого пиксела изменяется на цвет заполнения. Потом анализируется цвет пикселов, соседних с предшествующими. И так далее, пока внутри контура все пикселы не перекрасятся в цвет заполнения. Пикселы контура образуют границу, за которую нельзя выходить в ходе последовательного перебора всех соседних пикселов. Соседними могут считаться только четыре пиксела (сосед справа, слева, сверху и снизу — четырехсвязность), или восемь пикселов (восьми-связность). Не всякий контур может считаться границей закрашивания, например, для восьмисвязного алгоритма (рис. 3. 36). 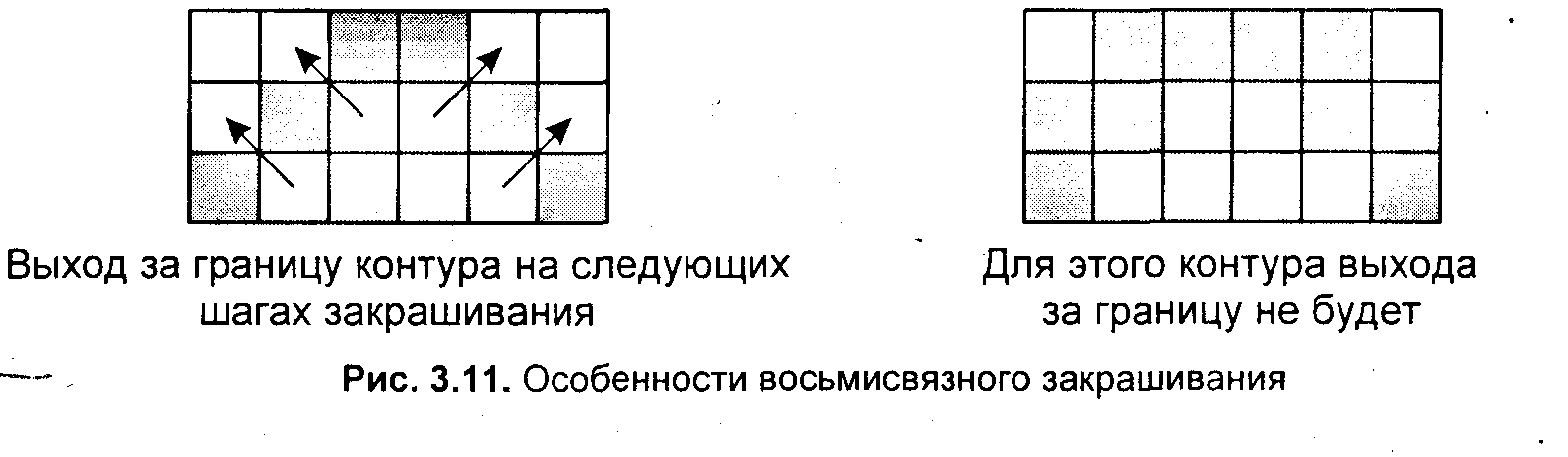 Рис. 3.36.Особенности восьмисвязного закрашивания - выход за границу контура на следующих шагах закрашивания Простейший алгоритм закрашивания. Для всех алгоритмов закрашивания нужно задавать начальную точку внутри контура с координатами х0, у0. Простейший алгоритм можно описать всего двумя шагами. Алгоритм закрашивания линиями. Данный алгоритм получил широкое распространение в компьютерной графике. От приведенного выше простейшего алгоритма он отличается тем, что на каждом шаге закрашивания рисуется горизонтальная линия, которая размещается между пикселами контура. Алгоритм также рекурсивный, но поскольку вызов функции осуществляется для линии, а не для каждого отдельного пиксела, то количество вложенных вызовов уменьшается пропорционально длине линии. Это уменьшает нагрузку на стековую память компьютера и обеспечивает высокую скорость работы. Пример работы алгоритма закрашивания линиями приведен на рис 3. 37. 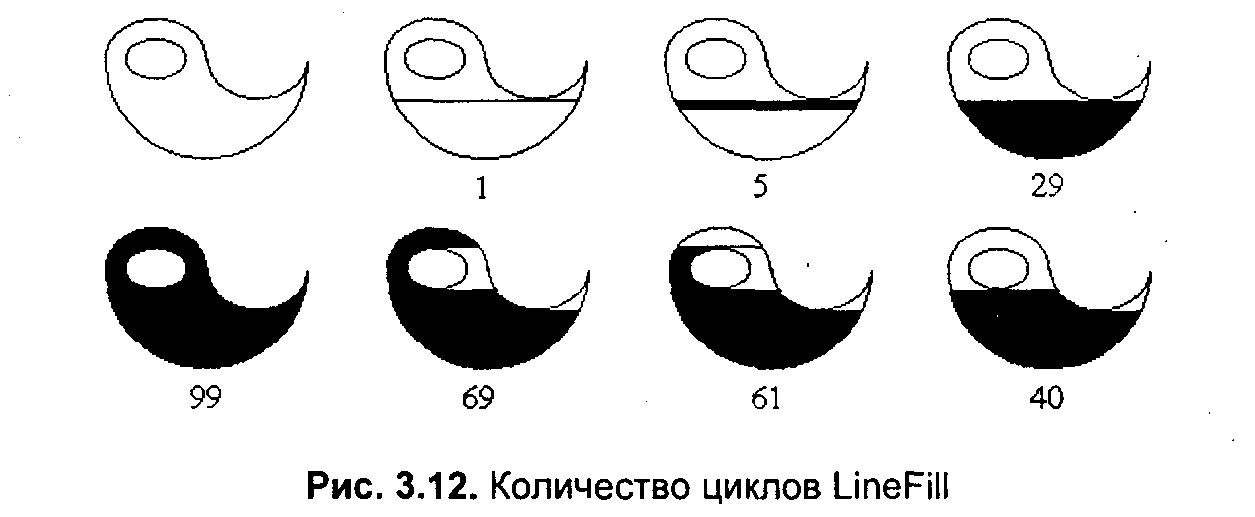 Рис. 3.37. Количество циклов LineFill Алгоритмы заполнения, которые используют математическое описание контура Математическим описанием контура фигуры может служить уравнение у =f(x) для контypa окружности, эллипса или другой кривой. Для многоугольника (полигона) контур задается множеством координат вершин (хi, уi). Возможны идругие формы описания контура. Общим для рассматриваемых ниже алгоритмов есть то, что для генерации точек заполнения не нужны предварительно сформированные в растре пикселы границы контура фигуры. Контур может вообще не рисоваться в растре ни до, ни после заполнения. 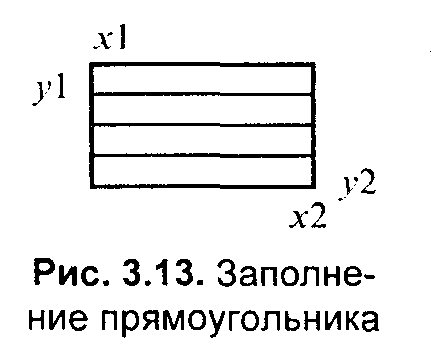 Рис. 3.38. Заполнение прямоугольника Заполнение прямоугольников. Среди всех фигур прямоугольник заполнять наиболее просто. Если прямоугольник задан координатами противоположных углов, например, левого верхнего (х1, у1) и правого нижнего (х2, у2), тогда алгоритм может состоять в последовательном рисовании горизонтальных линий заданного цвета (рис. 3. 38). Заполнение круга. Для заполнения круга можно использовать алгоритм вывода контура. В процессе выполнения этого алгоритма последовательно вычисляются координаты пикселов контура в границах одного октанта. Для заполнения следует выводить горизонтали, которые соединяют пары точек на контуре, расположенные симметрично относительно оси y (рис. 3.39, слева). Так же можно создать и алгоритм заполнения эллипса. Заполнение полигонов. Контур полигона определяется вершинами, которые соединены отрезками прямых — ребрами (рис. 3.39, справа). Это — векторная форма описания фигуры. Рассмотрим один из наиболее популярных алгоритмов заполнения полигона. Его основная идея — закрашивание фигуры отрезками прямых линий. Удобней использовать горизонтали. Алгоритм представляет собою цикл вдоль оси у, в ходе этого цикла выполняется поиск точек пересечения линии контура с соответствующими горизонталями. Этот алгоритм получил название XY . 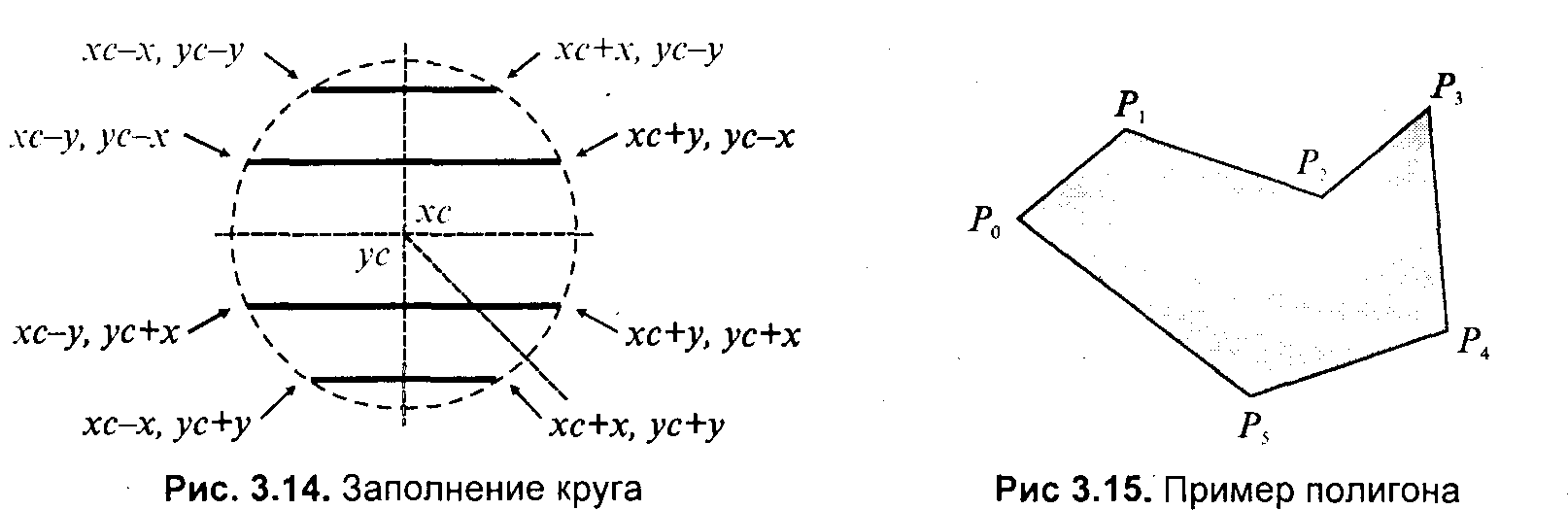 Рис. 3.39. Заполнение круга Пример полигона В этом алгоритме использовано топологическое свойство контура фигуры. Оно состоит в том, что любая прямая линия пересекает любой замкнутый контур четное количество раз (рис. 3.40). Для выпуклых фигур точек пересечения с любой прямой всегда две. 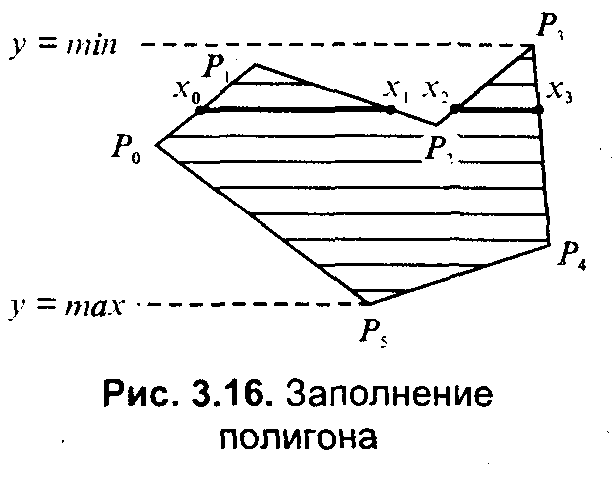 Рис. 3.40. Заполнение полигона При нахождении точек пересечения горизонтали с контуром необходимо принимать во внимание особые точки. Если горизонталь имеет координату (у), совпадающую с координатой yi вершины Рiтогда надлежит анализировать то, как горизонталь проходит через вершину. Если горизонталь при этом пересекает контур, как, например, в вершинах Р0 ли Р4, то в массив записывается одна точка пересечения. Если горизонталь касается вершины контура (в этом случае вершина соответствует локальному минимуму или максимуму, как, например, в вершинах Р1, Р2, Р3или Р5), тогда координата точки касания или Не записывается, или записывается в массив два раза. Это является условием четного количества точек пересечения, хранящихся в массиве {хj}. Процедура определения точек пересечения контура с горизонталью, учитывая анализ на локальный максимум, может быть достаточно сложной. Это замедляет работу. Радикальным решением для упрощения поиска точек пересечения может быть сдвиг координат вершин контура или горизонталей заполнения таким образом, чтобы ни одна горизонталь не попала в вершину. Сдвиг можно выполнять разными способами, например, ввести в растр дробные координаты для горизонталей; ymin+ 0. 5, ymin+ 1. 5,..., ymin - 0. 5. Но такое упрощение процедуры нахождения точек пересечения приводит к некоторому искажению формы полигона. Для определения координат (х) точек пересечения для каждой горизонтали необходимо перебирать все η ребер контура. Координата пересечения peбра pi - pk c горизонталью (у) равняется x = xi + (уk - у)(хк- хi )/(уk - уi). Количество тактов работы этого алгоритма: где ymax, ymin— диапазон координат y, Νгоρ— число тактов, нужных для одной горизонтали. Оценим величину Νгоρ как пропорциональную числу вершин где к— коэффициент пропорциональности, n— число вершин полигона. Возможна модификация приведенного алгоритма для ускорения его работы. Например, можно принять во внимание то, что каждая горизонталь обычно пересекает небольшое количество ребер контура. Поэтому, если при поиске точек пересечения делать предшествующий отбор ребер, которые находятся вокруг каждой горизонтали, то можно добиться уменьшения количества тактов работы с Nгор = к ∙nдо к. ∙nр, где np— количество отобранных ребер. Например, разделим диапазон ymin -ymax пополам. Если для диапазона от ymin до yср, составить список ребер (или вершин), попадающих в этот диапазон, то в список будет включено приблизительно вдвое меньшее количество, чем для всего диапазона от ymin до ymax. Почему приблизительно — ибо это зависит от размещения вершин контура полигона. Таким образом, при работе алгоритма для каждой горизонтали в диапазоне от ymin до yсруже нужно не (к. ∙ п) тактов, а (k · n/2). Аналогично для диапазона уср-ymах также можно составить список ребер, который также будет почти вдвое меньшим. Если принять, что подсчеты для каждой горизонтали теперь выполняются за вдвое меньшее количество тактов, а именно за (Nгор /2), то общее число тактов: где Νдоп— количество тактов, которые необходимы при создании списка ребер. Такой способ повышения быстродействия заполнения полигонов эффективен для большого количества вершин. Контур можно делить не пополам, а на более мелкие части — соответственно повышается скорость. Приведенные выше алгоритмы заполнения могут быть использованы не только для рисования фигур. На основе алгоритмов заполнения могут быть разработаны алгоритмы для других целей. Например, для определения площади фигуры (если считать площадь пропорциональной количеству пикселов заполнения). Или, например, алгоритм для поиска объектов по внутренней точке — эта операция часто используется в векторных графических редакторах. Логическое условие будет определять стиль линии. Например, если условием будет четность значения С, то получим линию из разрозненных точек. Для рисования пунктирной линии можно анализировать остаток от деления С на S. Например, если рисовать пикселы линии только при С mod S < S/2, то получим пунктирную линию с длиной штрихов S/2. шаг штрихов — S. При выводе полилиний, а также сплайновых кривых, аппроксимируемых прямолинейными отрезками, необходимо предотвратить обнуление значения счетчика в начале каждого отрезка и обеспечить продолжение непрерывного прироста вдоль всей сложной линии. Иначе будут нестыковки пунктира. Использование переменной-счетчика затруднено при генерации пунктирных линий в алгоритмах, которые используют симметрию, например, при выводе окружности или эллипса. Здесь необходимо обеспечивать стыковку пунктира на границах октантов или квадрантов. Стиль заполненияКисть и текстура При выводе фигур могут использоваться разные стили заполнения. Простейшее — сплошное заполнение — это когда все пикселы внутри контура фигуры имеют одинаковый цвет. Для обозначения стилей заполнения, отличных от сплошного, используют такие понятия, как кисть и текстура. Их можно считать синонимами, однако, понятие «текстура» обычно используется применительно к трехмерным объектам, а "кисть" — при изображении двумерных объектов. Текстура — это стиль заполнения, закрашивание, которое имитирует внешний вид, материал поверхности, рельефность трехмерного объекта. Для описания алгоритмов заполнения фигур в определенном стиле, используем тот же способ, что и для описания алгоритмов рисования линий. Мы уже ранее рассмотрели некоторые алгоритмы заполнения, и описание всех разновидностей подобных алгоритмов можно дать с помощью такой обобщенной схемы: Например, в алгоритме вывода полигонов пикселы заполнения рисуются в теле цикла горизонталей, а все другие операции предназначены для расчета координат (х, у) этих пикселов. При сплошном заполнении С = const. Для других стилей нам нужно в течение цикла вывода фигуры как-то изменять цвет пикселов заполнения, чтобы получить определенный узор. Преобразуем алгоритм заполнения таким образом: 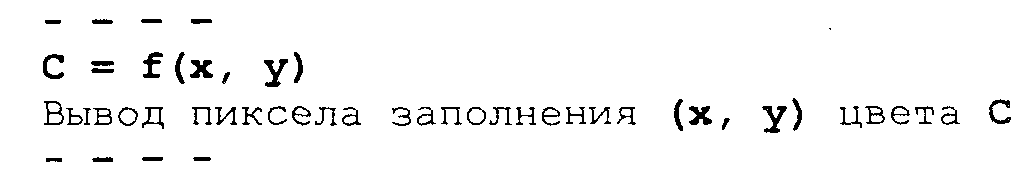 Функция ƒ(х, у) будет определять стиль заполнения. Аргументами функции цвета являются координаты текущего пиксела заполнения. Однако в отдельных случаях эти аргументы не нужны. Например, если цвет С вычислять как случайное значение в определенных границах: С = random(), то можно создать иллюзию шершавой матовой поверхности (рис. 3.41). Другой стиль заполнения — штриховой (рис. 3.42). Для него функцию цвета также можно записать в аналитической форме: где S — период, а Τ — толщина штрихов, Сш — цвет штрихов, Сф — цвет фона. Если не рисовать пикселы фона, то можно создать иллюзию полупрозрачной фигуры. Подобную функцию можно записать и для других типов штриховки. Аналитическая форма описания стиля заполнения позволяет достаточно просто изменять размеры штрихов при изменении масштаба показа, что весьма удобно для использования, например, в векторных графических системах. Недостаток аналитической формы - сложность формул для описания естественных материалов, поскольку большое количество вычислительных операций на каждый пиксел заполнения существенно уменьшает скорость визуализации.  Рис. 3.41. Матовая поверхность  Рис. 3.42. Штриховка Наиболее часто при использовании кистей и текстур используется наложение специально изготовленных растровых изображений. Такой алгоритм заполнения можно описать вышеупомянутой общей схемой, если строку С =f(x,у) заменить двумя другими строками: 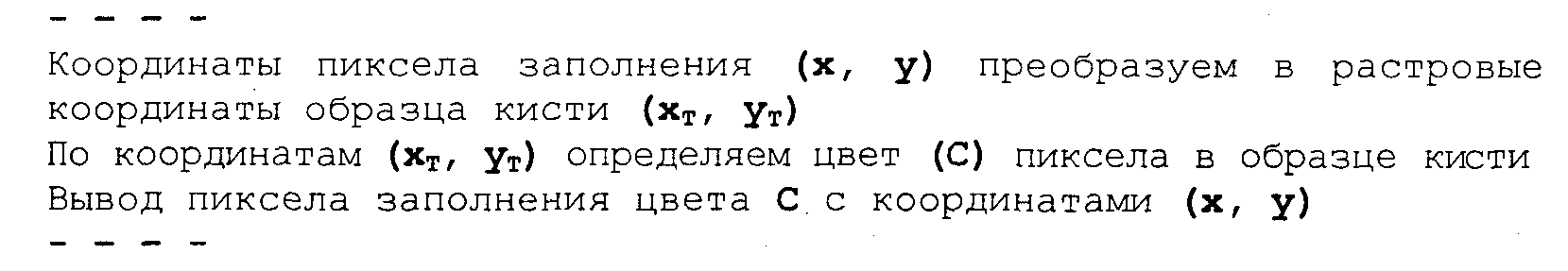 Преобразование координат пиксела заполнения (х, у) в координаты внутри образца кисти можно выполнить таким образом: где т, η — размеры растра образца кисти по горизонтали и вертикали. При этом координаты (хТ, уТ) попадают в диапазон хТ = 0... m - 1, уТ = 0... n - 1 при любых значениях х и у. Таким образом, обеспечивается циклическое копирование фрагментов кисти внутри области заполнения фигуры (рис. 3.43). 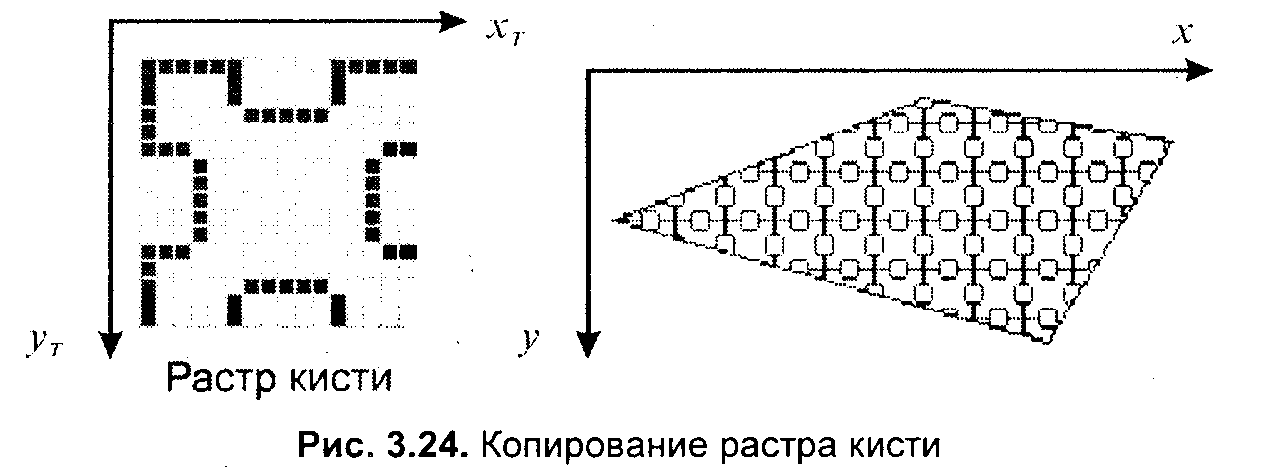 Рис. 3.43. Копирование растра кисти Удобно, когда размеры кисти равняются степени двойки. В этом случае вместо операций взятия остатка (mod) можно использовать более быстрые для цифровых компьютеров поразрядные двоичные операции. Приведем пример быстрого вычисления остатка от деления на 16. 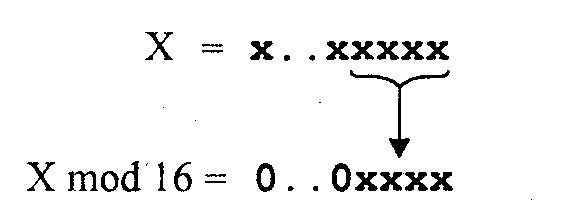 Еще один пример. Если необходимо вычислить (X mod 256), а значение X записано в регистре АХ микропроцессора (совместимого с 80x86), то для выполнения такой операции достаточно взять содержимое младшей байтовой части этого регистра — AL. Для пикселов текстур часто употребляется название тексел. Растровые текстуры и кисти широко используются в современной компьютерной графике, в том числе и в 3D-графике. Для отображения трехмерных объектов часто применяются полигональные поверхности, каждая грань отображается с наложенной текстурой. Поскольку объекты обычно показываются из разных ракурсов — повороты, изменения размеров и т. п., необходимо соответственно трансформировать и каждую грань с текстурой. Для этого используются проективные текстуры. Общая схема алгоритма заполнения контуров полигонов для проективных текстур такая же, как приведенная выше. Однако растровый образец здесь представляет всю грань, а преобразование координат из (х, у) в (хT, уT) сложнее. Для параллельной проекции можно использовать аффинное преобразование: где коэффициенты A, В,..., F являются константами при пересчете координат всех пикселов для отдельной текстурированной грани. Такое преобразование координат можно использовать, если привязать текстуру к грани по трем опорным точкам. Пример наложения проективной текстуры приведен на рис. 3.44.  Рис. 3.44. Наложение проективной текстуры (1,2, 3 - опорные точки грани) Привязывание по трем точкам соответствует системе уравнений где i = 1, 2, 3. По известным координатам (хTi, yTi )и (хi, уi ) можно найти коэффициенты А, В,..., F, если решить систему линейных уравнений. Эта система распадается на две независимые системы третьего порядка. Для упрощения записи заменим xTi, на Хiа уTiна Yi,:  Для решения систем линейных уравнений известно много способов. Используем способ детерминантов. Решение первой системы для коэффициентов А, В и С можно записать в виде: 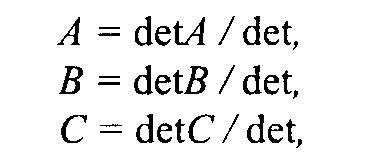 где 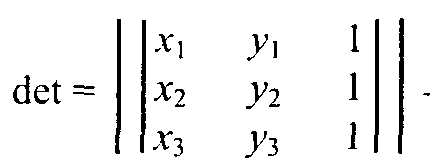 —это главный детерминант системы, —это главный детерминант системы,а детерминанты dеtA, dеtBи detCполучаются заменой соответствующих столбцов в det столбцом свободных членов Если главный детерминант равняется нулю, то это означает; что решить систему невозможно. Это может быть, например, тогда, когда все три точки (х1, y1), (х2, y2) и (х3, у3) располагаются вдоль прямой линии. Однако в этом случае рисовать текстуру и не нужно — грань мы видим с торца. Вычислить детерминант третьей степени можно, например, с помощью "правила Саррюса" . Для этого справа нужно дописать первые два столбца, а потом прибавить (отнять) произведение по диагоналям:  Вычислим главный детерминант Преобразуем выражение так, чтобы уменьшить количество умножений: Аналогично вычисляются detAи detB. Детерминант detC - самый сложный. Но его вычислять не обязательно. Запишем решение системы в следующем виде: Таким же способом решаем систему уравнений для D, Ε и F. 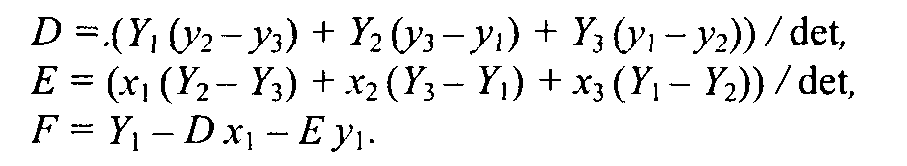 Заметьте, что здесь главный детерминант detсовпадает с детерминантом первой системы уравнений — для А, В иС. Наложение текстур в центральной (перспективной) проекции осуществляется сложнее, чем в параллельной проекции. Рассмотрим рис. 3.45, на котором изображен текстурированный прямоугольник.  Рис. 3.45. Прямоугольник в разных проекциях Прямоугольник в параллельной проекции всегда выглядит как параллелограмм, поскольку для этой проекции сохраняется параллельность прямых и отношение длин. В перспективной (центральной) проекции это уже не параллелограмм и не трапеция (в косоугольной — трапеция), поскольку параллельность и отношение длин здесь не сохраняются. А что сохраняется? Как изображать плоские грани? В предидущих главах были рассматрены проекции на плоскость. Для таких проекций прямые линии остаются прямыми линиями, поэтому грани можно выводить как полигоны. Здесь уместно вспомнить, как формируется изображение в определенной проекции средствами компьютерной графики. Последовательность преобразований координат выглядит так:  Если считать, что точки текстуры должны соответствовать точкам на объекте, то координаты текстуры должны связываться с мировыми координатами. Поскольку для параллельной проекции в цепочке от мировых координат к экранным все преобразования линейные, то целиком допустимо связать координаты текстуры с экранными координатами одним аффинным преобразованиям. Для перспективной проекции так делать нельзя. Преобразование координат из видовых — в координаты плоскости проецирования — нелинейное. Поэтому экранные координаты сначала следует преобразовать в такие, которые линейно связаны с мировыми — это могут быть, например, видовые. А потом видовые координаты (или непосредственно мировые) связать с координатами текстуры аффинным преобразованием, используя, например, метод трех точек. Рассмотрим, как можно выводить в перспективной проекции полигон с текстурой. Будем использовать алгоритм заполнения полигона горизонтальными линиями, раньше уже рассмотренный нами. На рис. 3.46 изображена одна из горизонталей (АВ). Вершины полигона (1-2-3-4) здесь заданы экранными двумерными координатами. Для краткости изложения будем считать, что экранные координаты совпадают с координатами в плоскости проецирования. В ходе вывода полигона для связи с текстурой будем вычислять видовые координаты произвольной точки (Р) этого полигона. Для этого будем использовать как базовую такую операцию: по известным видовым координатам концов отрезка находим видовые координаты точки отрезка, заданной координатами в плоскости проецирования. 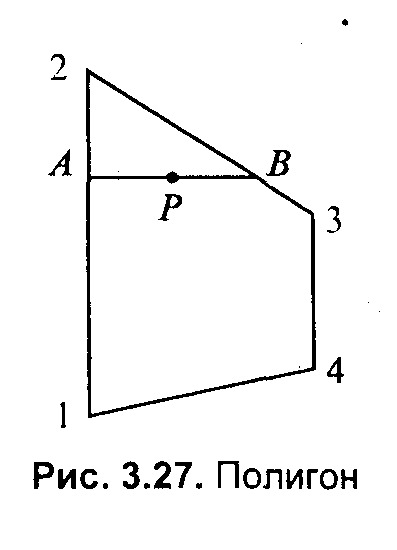 Рис. 3.46. Полигон Для определения видовых координат X, Y, Ζ точки А должны быть известны видовые координаты концов отрезка (1-2). Для видовых координат справедливы соотношения: Выберем пропорцию, которая связывает, например, координаты Х и Ζ. Тогда где Теперь запишем для перспективной проекции соотношения между видовыми координатами произвольной точки и координатой Хnв плоскости проецирования: где Zk— это координата камеры (точки схода лучей проецирования), Znл — координата плоскости проецирования. Перепишем это уравнение так: где Решением системы будет: после чего вычисляется X, например, по формуле X = а + Zb. Для определения координаты Υ достаточно заменить всюду в формулах Xна Υ. Здесь можно заметить, что вычисление видовых координат (X. Υ, Ζ) по известным координатам проекции соответствует обратному проективному преобразованию. Найдя видовые координаты точки А, мы можем так же вычислить видовые координаты и для точки В, лежащей на отрезке (3-4). Аналогично определяются видовые координаты точки Р. Следует отметить, что для преобразования координат необходимо вычислять дробно-линейные выражения, что может существенно замедлить цикл визуализации. Поэтому часто используют упрощенные вычисления координат. Также используется комбинирование методов — для небольших треугольных граней (которые являются небольшими в текущем ракурсе обзора) используют только аффинные преобразование, а для больших полигонов выполняют вычисления с учетом перспективы. Для наложения текстур на поверхности объектов используются и другие преобразования координат. Если в ходе анимации изменять координаты привязывания текстуры, то можно получить интересные видеоэффекты. Одна из проблем наложения текстур состоит в том, что преобразования растровых образцов (повороты, изменение размеров и т. п.) приводят к ухудшению качества изображения. Повороты растра прибавляют ступенчатости {aliasing); увеличение размеров укрупняет пикселы, а уменьшение размеров растра приводит к потере многих пикселов образца текстуры, появляется муар. Одним из методов улучшения визуализации текстурированных объектов является использование нескольких образцов текстур с разной детализацией — MIPmaps (MIPот лат. MultumInParvo— много в одном). Компьютерная система в течение цикла визуализации сама выбирает подходящий образец текстуры с нужной разрешающей способностью. Для улучшения текстурированных изображений также используют методы фильтрации растров текстур, например, билинейную фильтрацию (рис. 3.47). Билинейная фильтрация выполняется так. Пусть текущий тексел имеет координаты х, у. Сначала интерполируются соответственно координате xцвета пар ближайших пикселов А-В и C-D. Потом выполняется интерполяция полученных значений соответственно координате y. Также используются другие, более сложные способы фильтрации, например, трилинейная и анизотропная фильтрация. Трилинейная фильтрация объединяет билинейную фильтрацию и интерполяцию разных уровней текстур MIPmaps. Анизотропная фильтрация — самая совершенная, она учитывает также текущую пространственную ориентацию текстурированных граней. 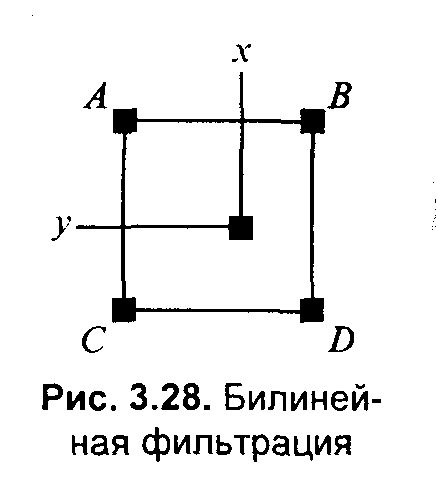 Рис. 3.47. Билинейная фильтрация При использовании текстур необходим достаточный объем памяти компьютера — количество растровых образцов может достигать десятков, сотен в зависимости от количества типов объектов и многообразия пространственных сцен. Чтобы как можно быстрее создавать изображение, необходимо сохранять текстуры в оперативной памяти, а если это позволяет видеоадаптер — то в памяти видеоадаптера. Для экономии памяти, которая выделяется для текстур, можно использовать блочное текстурирование. Текстура здесь уже не представляет всю грань целиком, а лишь отдельный фрагмент, который циклически повторяется в грани. Это делается так же, как размножение рисунка кисти при закрашивании полигонов, которые уже рассмотрены нами в этом параграфе. Разумеется, не для всех объектов можно использовать такой способ отображения, однако, например, для образцов массовой "коробочной" архитектуры в этом плане есть практически неограниченные возможности (рис. 3.48).  Рис. 3.48. Блочное текстурирование При формировании растровых изображений объектов главное — для любого пиксела объекта установить нужный цвет. Иногда не очень важно, какой именно метод используется для расчетов цветов. Например, можно моделировать законы оптики и на основе определенных моделей делать расчеты освещения объектов в ходе цикла визуализации. Тем не менее, например, для компьютерной игры это можно осуществить намного более легким способом — просто наложить предварительно изготовленную текстуру. В сцене, которая изображена на рис. 3.49, расположение двух источников света не меняется, поэтому текстура для газона вокруг домика может использоваться для любого ракурса показа.  Рис. 3.49. Текстура как карта освещения и теней Поскольку обычно наложение текстуры осуществляется быстрее создания теней путем геометрических расчетов или трассировки лучей, то это позволяет достичь высокой скорости визуализации. Однако, на этом пути возникают проблемы обеспечения надлежащей разрешающей способности текстуры. Приведем еще один пример использования текстуры — в качестве карты прозрачности. Цвет любого пиксела текстуры здесь определяет прозрачность соответствующей точки поверхности объекта (рис. 3.50).  Рис. 3.50. Текстура - карта прозрачности для поверхности тора Можно также использовать текстуру для имитации зеркального отражения, однако, ее корректное использование возможно только для одного ракурса обзора объектов. Известны также текстуры для имитации рельефа {BumpMapping). Иллюзия искривления поверхности средствами bump-текстурирования достигается изменением направления нормали. Нормаль к поверхности для каждой точки изменяется соответственно значению тексела. Таким образом можно имитировать, например, волны. Поскольку иллюзия рельефности здесь создается не искривлением поверхности, а только соответствующей локальной подсветкой или затемнением, то возможности отображения рельефа методом bитр-текстурирования существенно ограничены, в том числе и ракурсом показа. Если смотреть на плоскую грань с торца, то она — плоская, как ее не закрась. Таким образом, для задания многих свойств поверхности объекта можно использовать одну или несколько текстур. В настоящее время употребляется термин multitexturing— многослойное наложение текстур. Наложение двух и больше текстур предусматривает задание определенной функции комбинирования (смешивания) текселов. Безусловно, можно предложить и более сложные способы наложения многослойных текстур - надо разрабатывать соответствующие функции комбинирования. Можно считать, что здесь мы снова возвращаемся к аналитическому, процедурному, описанию стиля заполнения - только теперь мы используем в формулах также и текстуры. Шейдеры Развитие методов и технологий текстурирования, стремление использовать гибкие процедурные методы закрашивания привели к появлению понятия шейдер. Шейдер (от англ. shade— затемнять, здесь не путать shadeс shadow— тень, шейдер затемняет, а не затеняет — для получения изображения теней от объектов в графике используются пока что не шейдеры, а другие средства) — это небольшая программа, которая содержит набор инструкции для расчета цветов пикселов объектов в ходе цикла визуализации. Фактически, шейдеры, немного в другом виде, использовались уже давно в графических пакетах для создания спецэффектов в кино (например, в пакете Maya). При создании спецэффектов для записи кадров кинофильма не очень нужен режим реального времени, каждый кадр может генерироваться минуту и дольше, главное здесь — это качество изображения. В 2001-2002 гг. для массового употребления, в первую очередь для компьютерных игр, начали производиться видеоадаптеры (nVidia GeForce3, ATI Radeon 8500), которые аппа-ратно поддерживают базовые операции шейдеров. Разработчики графических программ заинтересовались гибкими возможностями шейдеров, поскольку ощущалась ограниченность фиксированного набора процедур графического конвейера. Возможность программирова-ния графических процессоров дает новый толчок развития средств компьютерной графики. Современные графические процессоры способны выполнять для любого пиксела десятки и сотни шейдерных команд в реальном времени. Сейчас существуют два типа шейдеров — вершинные (vertexshaders) и пиксельные (pixelshaders). Вершинные шейдеры предназначены для вычисления координат вершин полигонов и выполнения расчетов освещения, например, методом Гуро. Их можно считать альтернативой для стандартных возможностей аппаратных средств T&L (transformandlighting). Вершинный шейдер может обрабатывать все данные, относящиеся к одной вершине — координаты вершины, координаты нормали, текстурные координаты, цвет, освещение и т. п. Пиксельные шейдеры появились сначала как способ описания наложения пикселов многослойных текстур. Теперь они содержат разнообразные операции обработки цветов отдельных пикселов. Шейдеры оперируют такими типами данных — целые числа, числа с плавающей тонкой, тройки RGB, векторы, матрицы. Приведем формат одной команды шейдера для DirectX Graphics где: op — имя команды, Как видим, язык команд шейдеров фактически является ассемблером. Для разработки шейдерных программ можно использовать API DirectX (8. 0 и следующих версий), OpenGL 2. 0 (шейдерные операции частично поддерживаются в расширениях OpenGL версий 1. 2 и 1. 3). Также разработаны специальные языки программирования для шейдеров, например, Cg от nVidia . Общие сведения о шейдерных возможностях некоторых современных видеоадаптеров предоставлены в таблице 3. 2. Таблица 3. 2. Характеристики шейдерных возможностей видеоадаптеров
|
