Конспект лекций по компьютерной графике. Конспект лекций по дисциплине Компьютерная графика

• Название: Конспект лекций по дисциплине Компьютерная графика
• Анкор: Конспект лекций по компьютерной графике.doc
• Дата: 22.04.2017
• Размер: 16.3 Mb.
• Имя файла: Конспект лекций по компьютерной графике.doc
• Тип: Конспект лекций; #5372
• страница: 24 из 46

Глава 8. Реалистическое представление сцен

Основные направления реалистического представления сцен трехмерной графики определяются как:
 синтез реалистичных изображений,

 реалистическое оживление синтезированных объектов (анимация).

В этом разделе будут рассмотрены только некоторые базовые методы синтеза реалистических изображений:

 Модели освещения
 Модели закраски
 Трассировка лучей
 Имитация микрорельефа

 Механизмы отражения света

Другие методы синтеза – прозрачность, тени, задание фактуры, излучательность и т.д. выносятся на самостоятельное изучение.

8.1 Закрашивание поверхностей

В этом разделе мы рассмотрим методы, которые позволяют получить более-менее реа­листичное изображение для объектов, которые моделируются многогранниками и полиго­нальными сетками.

8.1.1 Модели отражения света

Рассмотрим, как можно определить цвет пикселов изображения поверхности в соответ­ствии с интенсивностью отраженного света при учете взаимного расположения поверхно­сти, источника света и наблюдателя.

Зеркальное отражение света. Угол между нормалью и падающим лучом равняется углу между нормалью и отраженным лучом. Падающий луч, отраженный луч и нормаль располагаются в одной плоскости (рис. 8.1).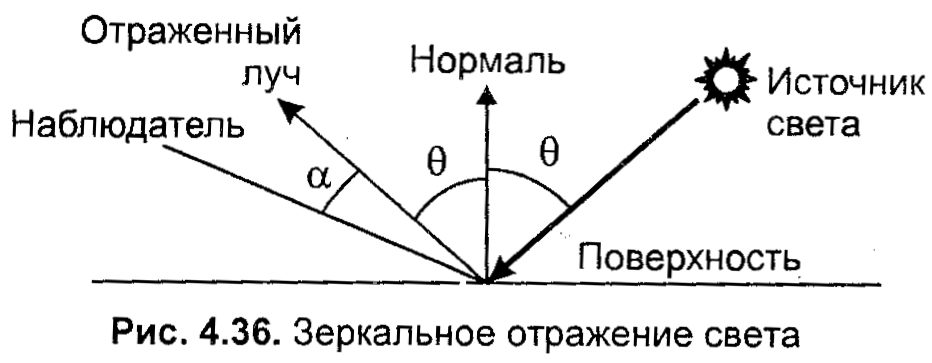


Рис. 8.1. Зеркальное отражение света

Поверхность считается идеально зеркальной, если на ней отсутствуют какие-либо неровности, шероховато­сти. Собственный цвет у такой поверх­ности не наблюдается. Световая энер­гия падающего луча отражается только по линии отраженного луча. Любое рассеивание в стороны от этой линии отсутствует. В природе, вероятно, нет идеально гладких поверхностей, поэтому полагают следующее: если глубина шероховато­стей существенно меньше длины волны излучения, то рассеивание не наблюдается. Для ви­димого спектра можно принять, что глубина шероховатости поверхности зеркала должна быть меньше 0.5 мкм.

Если поверхность зеркала отполирована неидеально, то наблюдается зависимость ин­тенсивности отраженного света от длины волны — чем больше длина волны, тем лучшее отражение. Например, красные лучи отражаются сильнее, чем синие.

При наличии шероховатости есть зависимость интенсивности отраженного света от угла падения. Отражение света максимально для углов Э, близких к 90 градусам.

Рис. 8.2. Примры для разных значений показателя p модели Фонга
Падающий луч, попадая на шероховатую поверхность реального зеркала, порождает не один отраженный луч, а несколько лучей, которые рассеиваются в разных направлениях. Зона рассеивания зависит от качества полировки и может быть описана некоторым законом распределения. Как правило, форма зоны рассеивания симметрична относительно линии идеального зеркально отраженного луча. К числу простейших, но довольно часто исполь­зуемых, относится эмпирическая модель Фонга, соответственно которой интенсивность зеркально отраженного излучения пропорциональна (cosa) где а — угол отклонения от линии идеально отраженного луча. Показатель находится в диапазоне от 1 до 1000 и зави­сит от качества полировки. Запишем это таким образом:

Is = I cos ^p ,

где I - интенсивность излучения источника




Диффузное отражение. Этот вид отражения присущ матовым поверхностям. Матовой можно считать такую поверхность, размер шероховатостей которой уже настолько боль­шой, что падающий луч рассеивается равномерно во все стороны. Такой тип отражения ха­рактерен, например, для гипса, песка, бумаги. Диффузное отражение описывается законом Ламберта, согласно которому интенсивность отраженного света пропорциональна косину­су угла между направлением на точечный источник света и нормалью к поверхности:

Id = I cos,

где I— интенсивность источника света.

При создании реалистических изображений следует учитывать то, что в природе, веро­ятно, не существуют идеально зеркальные или идеально матовые поверхности. При изо­бражении объектов средствами компьютерной графики обычно моделируют сочетание зер­кальности и диффузного рассеивания в пропорции, характерной для конкретного материа­ла. В этом случае модель отражения записывают в виде взвешенной суммы диффузной и зеркальной составляющих:

где константы Kd и Кс определяют отражательные свойства определенного материала. Кон­станты Kd и Кс обычно принимают значения в диапазоне от 0 до 1, причем Kd + Кс = 1.

Соответственно этой формуле интенсивность отраженного света равняется нулю для не­которых углов  и . Однако в реальных сценах обычно нет абсолютно затемненных объек­тов, следует учитывать фоновое подсвечивание — освещение рассеянным светом, отражен­ным от других объектов (рис. 8.3).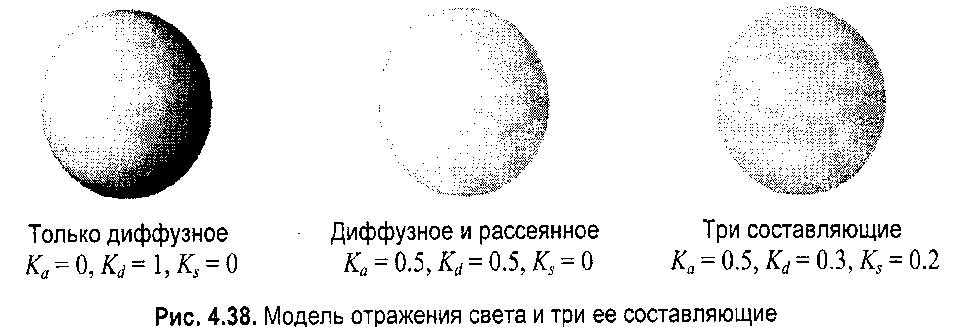

Рис. 8.3. Модель отражения света и три ее составляющие

В таком случае интенсивность может быть эмпирически выражена следующей формулой:

Iрез = IaKa + IdKd + IsKs = IaKa + I (Kd cos +Ks cos ^p )

где Ia - интенсивность рассеянного света, К_а— константа.

Можно еще усовершенствовать модель отражения, если учесть то, что энергия от источ­ника света уменьшается соответственно расстоянию до него




где R- расстояние от источника света до поверхности, F(R) — функция ослабления. Для точечного источника света энергия излучения уменьшается пропорционально квадрату рас­стояния. На практике обычно используют линейную аппроксимацию функции ослабления.

Для нескольких источников света диффузную и зеркальную составляющую рассчиты­вают в отдельности для каждого источника, а результат — сумма всех составляющих:

8.1.2 Вычисление нормалей и углов отражения

Вычисление координат вектора нормали. Рассматривая модели отражения света, вы, наверное, обратили внимание на то, что нормаль к поверхности — важный элемент. Опре­деление вектора нормали к поверхности в заданной точке может быть выполнено разными способами. В значительной степени это определяется типом модели описания поверхности. Для поверхностей, заданных в аналитической форме, известны методы дифференциальной геометрии, которые основываются на вычислении частных производных функций описа­ния. Например, если поверхность задана параметрическими функциями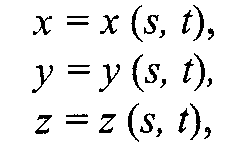



тогда координаты вектора нормали можно вычислить так: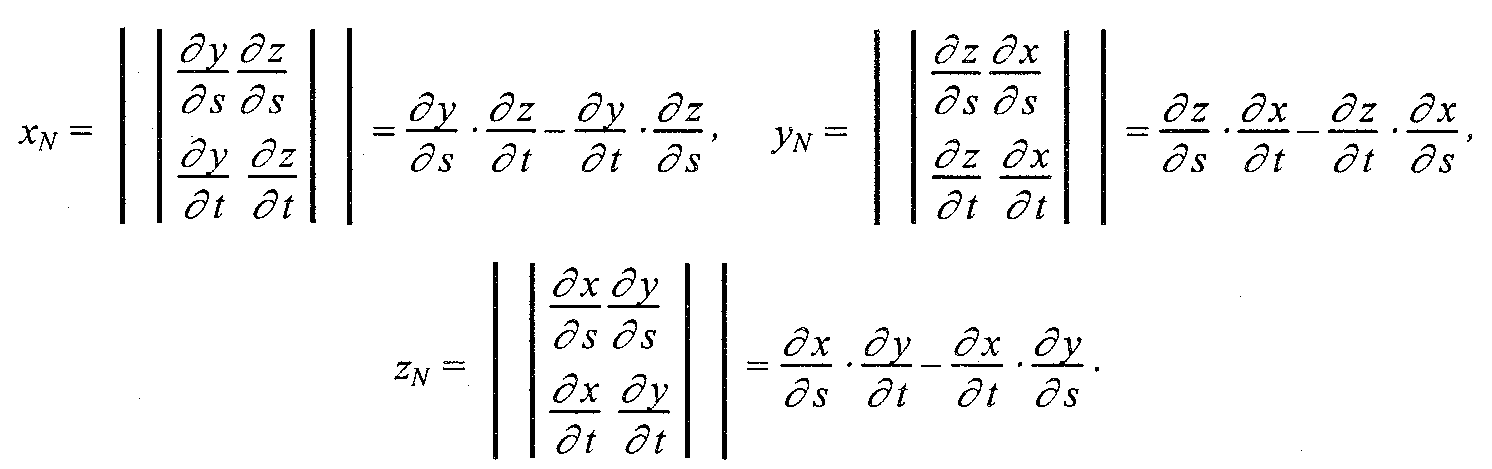



В случае описания поверхности векторно-полигональной моделью для определения нормалей можно использовать методы векторной алгебры.

Пусть в пространстве задана некоторая многогранная поверхность. Рассмотрим одну ее плоскую грань, имеющую вид треугольника (рис. 8.4).

Для вычисления координат вектора нормали воспользуемся векторным произведением любых двух векторов, которые лежат в плоскости грани. Такими векторами могут служить и ребра грани, например, ребра 1-2 и 1-3. Однако формулы для векторного произведения были определены нами только для радиус-векторов. Чтобы перейти к радиус-векторам, вве­дем новую систему координат, центр которой совпадает с вершиной 1, а оси — параллель­ны осям бывшей системы. Координаты вершин в новой системе: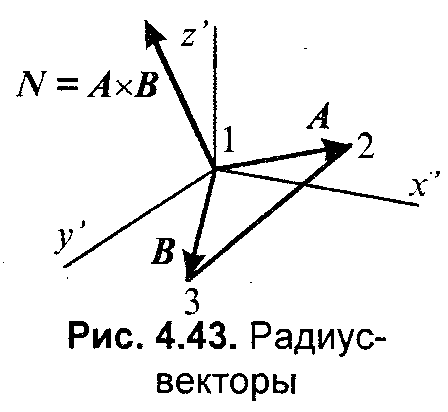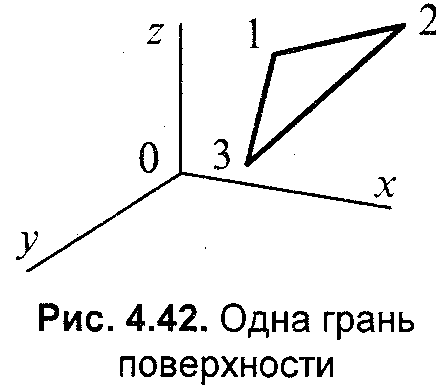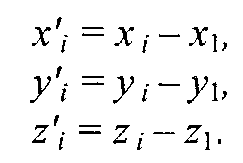







Рис. 8.4. Одна грань поверхности Радиус-векторы

Теперь назовем ребро (1-2) вектором А, а ребро (1-3) — векто­ром В, как показано на рис. 8.4. Таким образом, положение нор­мали к грани в пространстве будет описываться радиус-вектором N. Его координаты в системе (х', у', г') выразим формулами для векторного произведения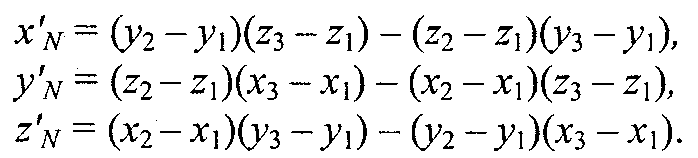


Плоская грань может быть изображена в разных ракурсах. В каждой конкретной ситуации необходимо выбирать направление нормали, которое соответствует видимой стороне грани. Если плоская грань может быть видна с обратной стороны, то тогда в расчетах отраженного света необходимо выбирать для нормали обратный вектор, то есть (-N).

Если полигональная поверхность имеет не треугольные грани, а, например, плоские че­тырехугольные, то расчет нормали можно выполнять по любым трем вершинам грани.

Диффузное отражение. Рассчитаем косинус угла между вектором нормали и направле­нием на источник света. Это можно выполнить таким способом.

Сначала необходимо определить радиус-вектор, направленный на источник света. Обо­значим его как S. Потом для вычисления косинуса угла между радиус-векторами S и N вос­пользуемся формулами скалярного произведения векторов. Поскольку




а также

то получим


Для упрощения вычислений целесообразно использовать векторы S и N единичной дли­ны, то есть |S|*|N| = 1.

Использование скалярного произведения здесь можно считать универсальным методом, который можно использовать для любого расположения точечного источника света. В от­дельных случаях можно рассчитать косинус угла падения по-иному. Например, если источ­ник света располагается на оси Zвидовых координат в бесконечности позади камеры, тогда косинус угла нормали к грани с осью Zравняется отношению координаты г и длины ради­ус-вектора нормали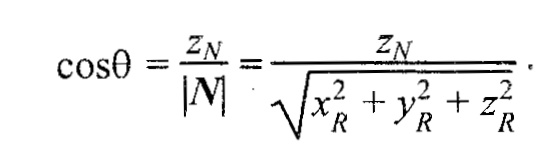



Зеркальное отражение. Будем считать, что задан радиус-вектор S, направленный на ис­точник света, а также известен радиус-вектор нормали N. Нужно найти косинус угла между отраженным лучом и направлением камеры.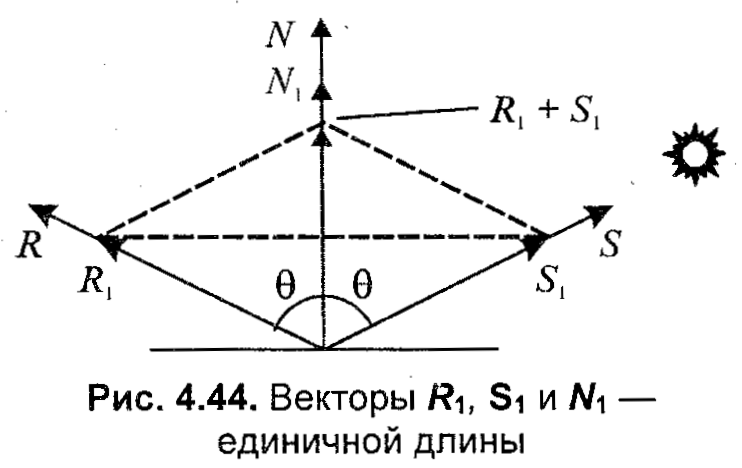

Сначала необходимо вычислить радиус-вектор отраженного луча. Обозначим его как R. Выпол­ним некоторые геометрические построения, как показано на рис. 8.5.

Рис. 8.5. Векторы R1, S1 и N1 –единичной длины
Для решения нашей задачи сначала рассмот­рим единичные векторы R1, S1, и N1. Поскольку векторы нормали, падающего луча и отраженного луча находятся в одной плоскости, то можно за­писать R1 + S1 = N¹, где N¹ — это вектор, который соответствует

диагонали ромба и совпадает по yаправлению с нормалью. Длина вектора N1 равняется 2cos. Поскольку вектор N¹ по на­правлению совпадает с N1, то

или



Отсюда находится единичный вектор отраженного луча:



Найдем cos. Для этого используем скалярное произведение векторов N и S:



Подставим это значение в выражение для R₁:


Полагая, что искомый вектор отраженного луча будет иметь такую же длину, что и вектор падающего луча, т.е. R = SR₁ , получим: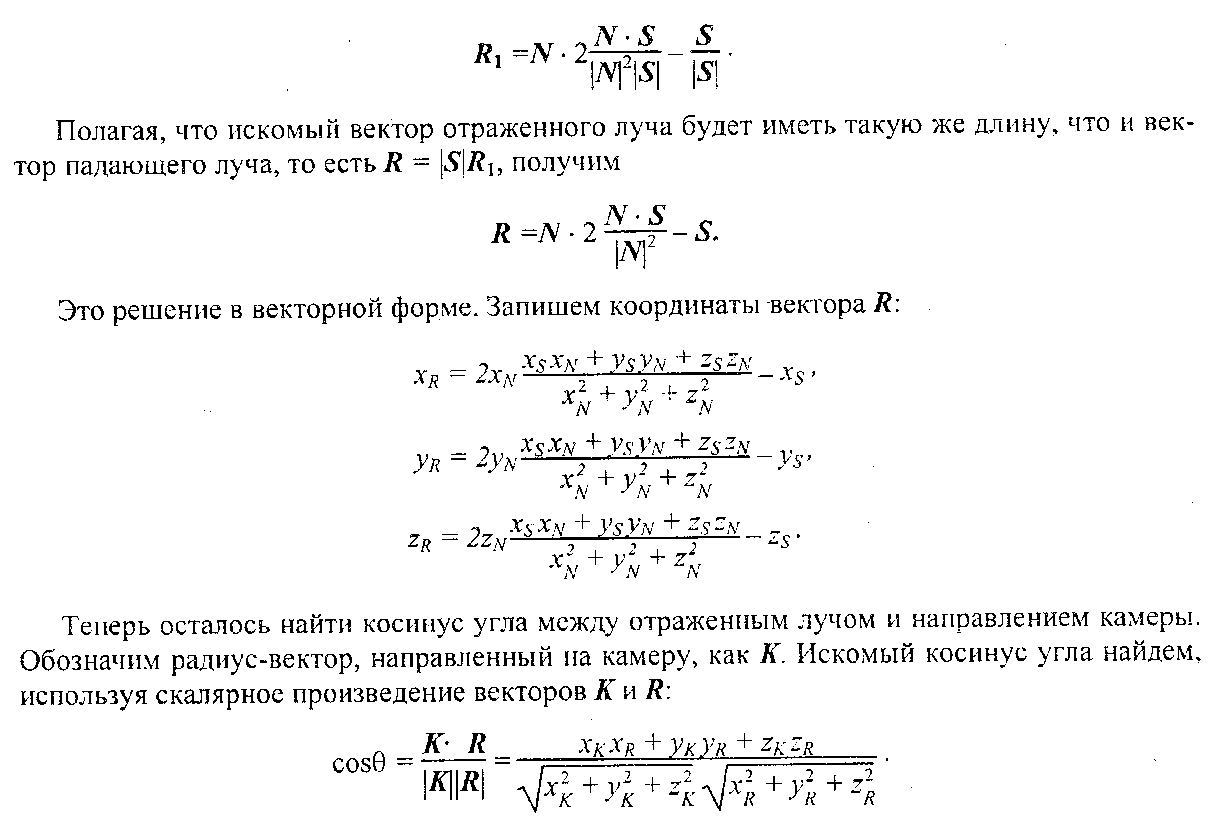




Это решение в векторной форме. Запишем координаты вектора R:

Теперь осталось найти косинус угла между отраженным лучом и направлением камеры. Пусть K – радиус-вектор, направленный на камеру. Найдем искомый косинус угла:



Для упрощения вычислений целесообразно задавать векторы S, N и Rединичной длины (тогда и Rбудет единичным).