Конспект лекций по компьютерной графике. Конспект лекций по дисциплине Компьютерная графика

• Название: Конспект лекций по дисциплине Компьютерная графика
• Анкор: Конспект лекций по компьютерной графике.doc
• Дата: 22.04.2017
• Размер: 16.3 Mb.
• Имя файла: Конспект лекций по компьютерной графике.doc
• Тип: Конспект лекций; #5372
• страница: 22 из 46

Глава 7. Методы и алгоритмы построения сложных трехмерных объектов

Понятие “трехмерная” графика в настоящее время можно считать наиболее распростра­ненным для обозначения темы, которая будет рассмотрена ниже (в литературе это название часто сокращается до "ЗD-графики"). Однако необходимо заметить, что такое название неточное, так как речь пойдет о создании изображения на плоскости, а не в объеме. Действительно трехмерные средства отображения пока что недостаточно широко распространены.

7.1 Модели описания поверхностей

Для описания формы поверхностей могут использоваться разнообразные методы. Сде­лаем обзор этих методов.

7.1.1. Аналитическая модель

Аналитической моделью будем называть описание поверхности математическими формулами. В КГ можно использовать много разновидностей такого описания. Например, в виде функции двух аргументов z = f(x, у). Можно использовать уравнение F(x, у, z) = 0.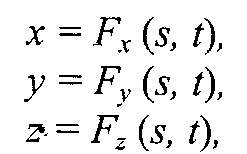

Наиболее часто используется параметрическая форма описания поверхности. Запишем формулы для трехмерной декартовой системы координат (x, у, z):
где s и t — параметры, которые изменяются в определенном диапазоне, а функции F_x, F_y,иF_zопределяют форму поверхности.

Преимущества параметрического описания — легко описывать поверхности, которые соответствуют неоднозначным функциям, замкнутые поверхности. Описание можно сде­лать таким образом, что формула не будет существенно изменяться при поворотах поверх­ности, масштабировании.

В качестве примера рассмотрим аналитическое описание поверхности шара. Сначала как функцию двух аргументов:

z = ±
В виде уравнения: x² + y² + z² - R²=0.

А также в параметрической форме:

x=Rsins cost,y=Rsins sint, z = R coss.

Для описания сложных поверхностей часто используют сплайны. Сплайн - это специ­альная функция, наиболее пригодная для аппроксимации отдельных фрагментов поверхно­сти. Несколько сплайнов образуют модель сложной поверхности. Другими словами, сплайн — эта тоже поверхность, но такая, для которой можно достаточно просто вычислить координаты ее точек. Обычно используют кубические сплайны. Почему именно кубиче­ские? Так как третья степень является наименьшей, позволяющей описывать любую форму, и при стыковке сплайнов можно обеспечить непрерывную первую производную — такая поверхность будет без излома в местах стыка. Сплайны часто определяют параметрически. Запишем формулу для координаты x(s,t)кубического сплайна в виде многочлена третьей степени параметров sи t: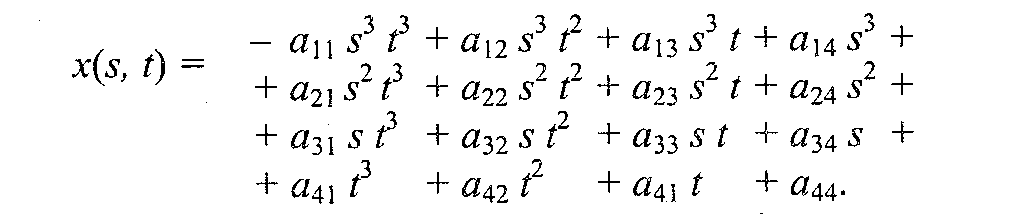



Для других координат можно записать подобные формулы — в виде функций y(s, t), z(s,t).

В математической литературе вы можете ознакомиться со способами определения ко­эффициентов a_ij для сплайнов, которые имеют заданные свойства.

Рассмотрим одну из разновидностей сплайнов — сплайн Безье. Приведем его сначала в обобщенной форме — степени тхп:

P(s,t) =

где Р_ij— опорные точки-ориентиры, 0≤s≤1, 0≤t≤1, и –коэффициенты биномаНьютона, они рассчитываются по формуле:

Кубический сплайн Безье соответствует т= 3, п = 3. Для его определения необходимы 16 точек-ориентиров Р_ij(рис. 7.1); коэффициенты и равняются 1,3, 3, 1 при i,j= 0,1,2,3.

Характеризуя аналитическую модель в целом, можно сказать, что эта модель наиболее пригодна для многих операций анализа поверхностей. С позиций КГ можно указать такие положительные черты: простота (впрочем, не всегда) расчета координат каждой точки по­верхности, нормали; небольшой объем информации для описания довольно сложных форм.

К недостаткам можно отнести: сложность формул описания с использованием функций, ко­торые медленно вычисляются в компьютере, снижают скорость выполнения операций отобра­жения; невозможность в большинстве случаев использования данной формы описания непо­средственно для построения изображения поверхности. В таких случаях поверхность обычно отображают как многогранник, используя формулы аналитического описания для расчета ко­ординат вершин граней в процессе отображения, что уменьшает скорость сравнительно с поли­гональной моделью описания.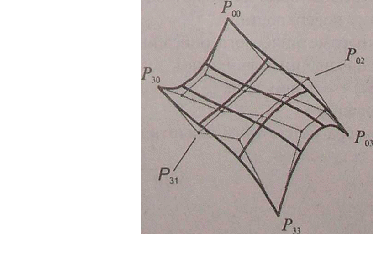




Рис. 7.1. Кубические сплайны Безье

7.1.2 Векторная полигональная модель

Для описания пространственных объектов здесь используются такие элементы: вершины, отрезки прямых (векторы), полилинии, полигоны, полигональные поверхности (рис. 7.2).

Элемент "вершина" (vertex) — главный элемент описания, все другие являются производ­ными. При использовании трехмерной декартовой системы координат вершины определяются как (x,y,z). Каждый объект однозначно определяется координатами собственных вершин.

Вершина может моделировать отдельный точечный объект, размер которого не имеет значения, а также может использоваться в качестве конечной точки для линейных объектов и полигонов. Двумя вершинами задается вектор.




Рис. 7.2. Элементы векторно-полигональной модели
Несколько векторов составляют полили­нию. Полилиния может моделировать отдельный линейный объект, толщина которого не учитывается, а также может представлять собой контур полигона.

Полигонмоделирует площадный объект. Один полигон может описывать плоскую грань объемного объекта. Не­сколько граней составляют объемный объект в виде полигональной поверхности — много­гранник или незамкнутую поверхность (в литературе часто употребляется название "поли­гональная сетка").

Векторную полигональную модель можно считать наиболее распространенной в со­временных системах трехмерной КГ. Ее используют в системах автоматизированного про­ектирования, в компьютерных играх, в геоинформационных системах и т. п.

Рассмотрим структуры данных, которые используются в векторной полигональной мо­дели. В качестве примера объекта будет куб. Рассмотрим, как можно организовать описа­ние такого объекта в структурах данных.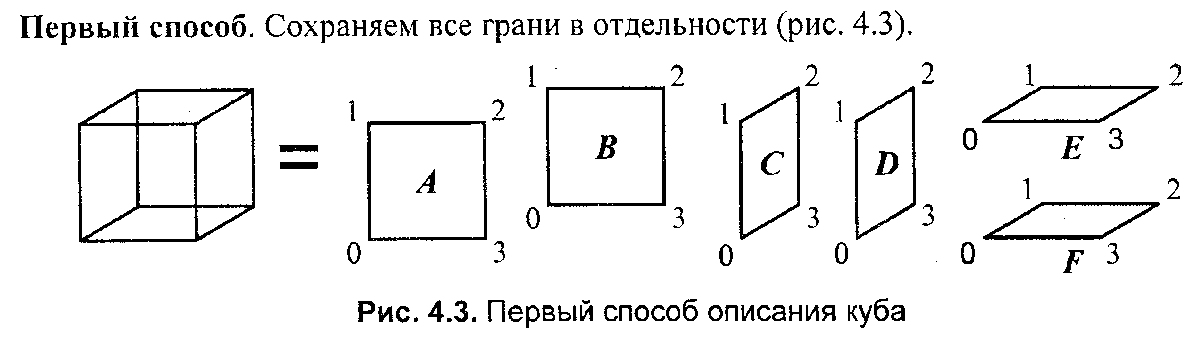

Рис. 7.3. Первый способ описания
П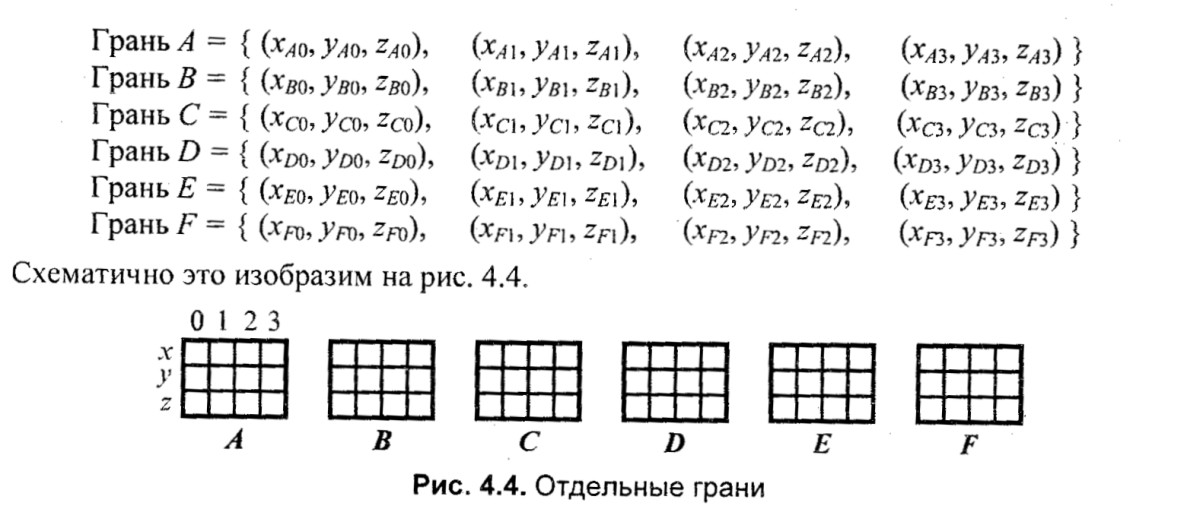
ервый способ. Сохраняем все грани в отдельности






Рис. 7.4. Отдельные грани
В компьютерной программе такой способ описания объекта можно реализовать разно­образно. Например, для каждой грани открывать в памяти отдельный массив. Можно все грани записывать в один массив-вектор (это уже лучше). А можно использовать классы (язык С++) как для описания отдельных граней, так и объектов в целом. Можно создавать структуры, которые объединяют тройки (x, у, z), или сохранять координаты в отдельности. Принципиально это мало что меняет — так или иначе в памяти необходимо сохранять ко­ординаты вершин граней плюс некоторую информацию в качестве накладных затрат.

Рассчитаем объем памяти, необходимый для описания куба указанным способом:

П₁ = 6 х 4 х 3 x Pв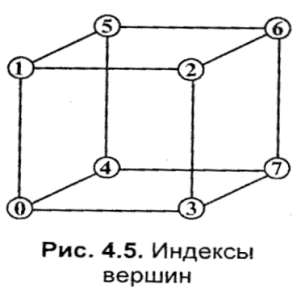

где Pв— разрядность чисел, которые используются для пред­ставления координат вершин. Шесть граней здесь описываются 24 вершинами. Такое пред­ставление избыточно — каждая вершина записана трижды. Не учитывается то, что у граней есть общие вершины.

Рис. 7.5. Индексы вершин
Второй способ описания. Для этого варианта координаты восьми вершин сохраняются без повторов. Вершины пронумеро­ваны (рис. 7.5), а каждая грань представлена в виде списка ин­дексов вершин (рис. 7.6).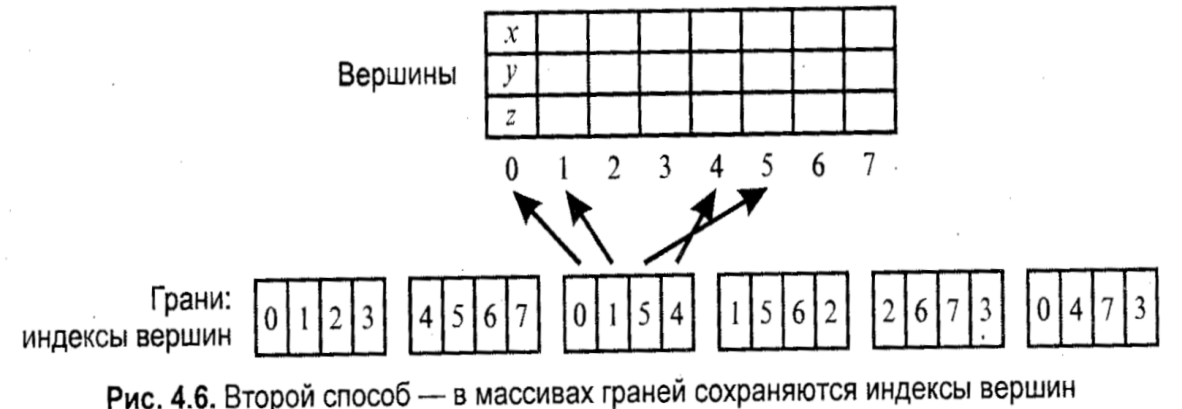



Рис. 7.6. Второй способ описаня

Оценим затраты памяти:

П2 = 8 x 3 x Pв +6 x 4 x Pиндекс

где Pв— разрядность координат, Pиндекс — разрядность индексов.

Третий способ. Пронумеруем также и ребра (рис. 7.7). Бу­дем сохранять грани в виде списка индексов ребер. Каждое ребро будет, в свою очередь, представлено списком индексов вершин. Этот способ в литературе иногда называют "линейно-узловой " моделью.

Оценим затраты памяти:

П₃ = 8 x 3 x Pв +12 x 2 x Pиндекс верш. +6 x4 x Риндекс ребер

где Pв - разрядность координат, Pиндекс верш. и Риндекс ребер - разрядность индексов вершин и ребер


Рис. 7.7. Индексы вершин и ребер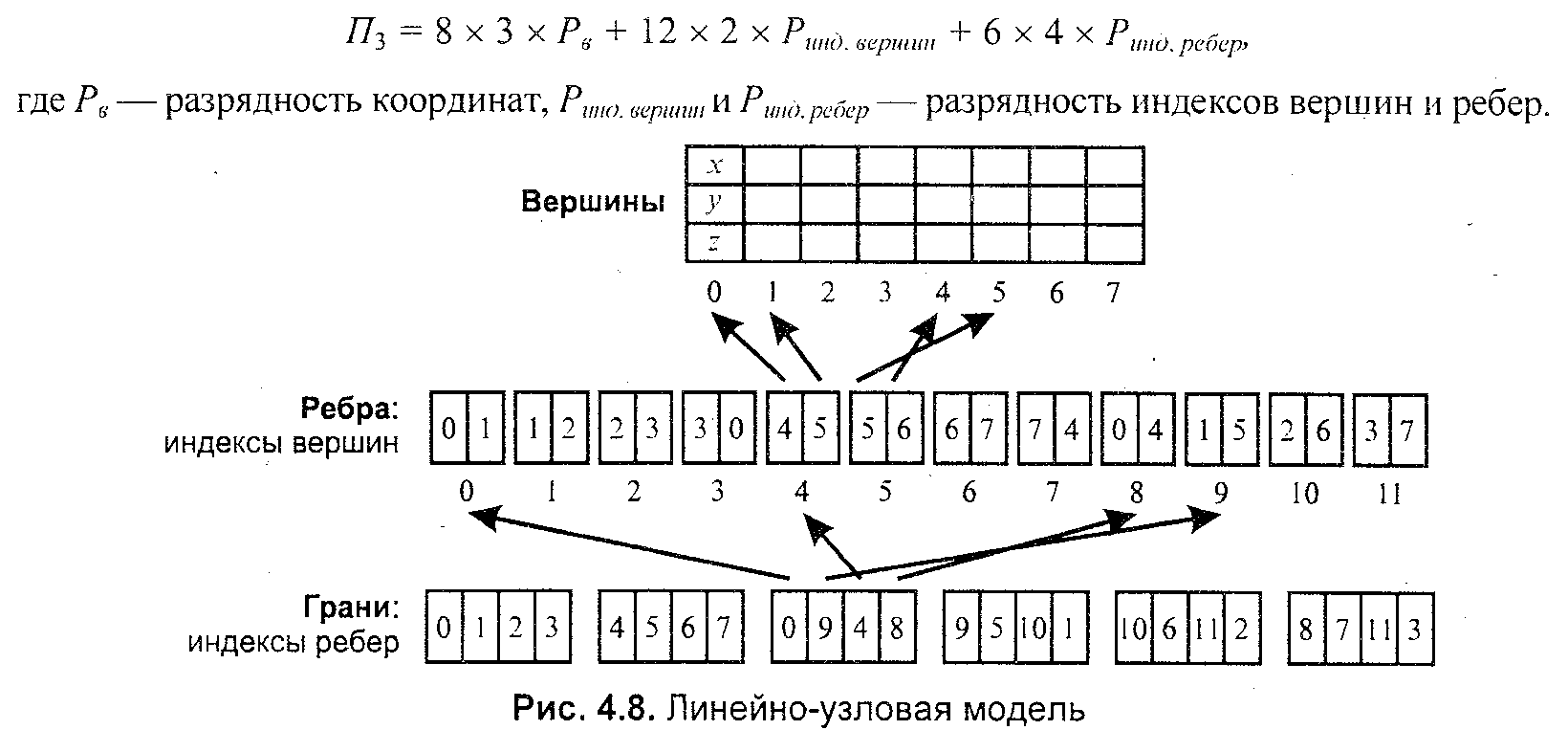




Рис. 7.8. Линейно-узловая модель

7.1.3 Воксельная модель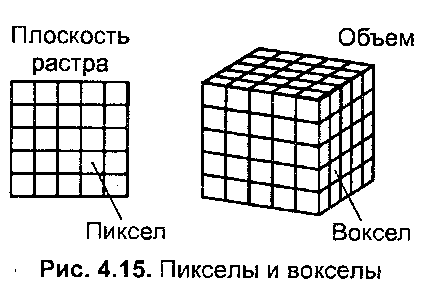

Воксельная модель – это трехмерный растр. Воксел это элемент объема. По аналогии с 2D растрами, состоящими из пикселов. Вокселы заполняют объем в трехмерном растре (рис.7.9)


Рис. 7.9. Пикселы и вокселы

Как мы знаем, любой пиксел должен иметь свой цвет. Любой воксел также имеет свой цвет, и, кроме того, прозрачность. Полная прозрачность воксела озна­чает пустоту соответствующей точки объема.

Поскольку вокселы располагаются в узлах равно­мерной сетки, то, обычно, чем меньше шаг сетки, тем большее количество вокселов помещается в опреде­ленном объеме, и тем меньший размер каждого от­дельного воксела. Основная характеристика вексель­ной модели — разрешающая способность — количест­во вокселов в определенном объеме. Она и определяет точность моделирования трехмер­ных объектов (рис. 7.10).

Для современной КГ вексельный метод считается одним из перспективных. Его исполь­зуют в компьютерных системах, предназначенных для медицинских целей.

Например, при сканировании томографом (computedtomography) получаются изображения срезов объекта, которые потом объединяются в виде объемной модели для дальнейшего анализа. Ве­ксельный метод используется в геологии, сейсмологии, в компьютерных играх. Во­кселы также используются для графических устройств отображения, которые создают дей­ствительно объемные изображения.

Положительные черты воксельной модели:

• 
  достаточно простое описание сложных объектов и сцен;
  
• 
  простая процедура отображения объемных сцен;
  

• 
  простое выполнение топологических операций над отдельными объектами и сценой в целом. Например, просто выполняется показ разреза — для этого соответствующие вокселы можно сделать прозрачными.
  

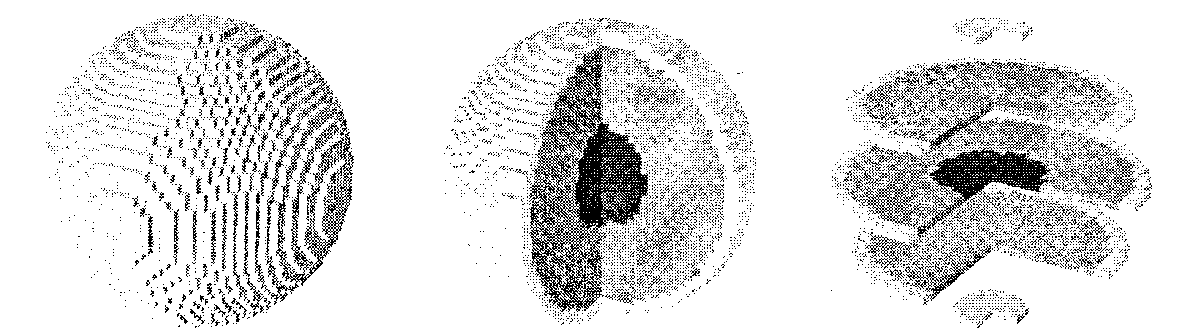Рис. 7.10. Воксельная модель шара и ее разрезы.

Недостатки воксельной модели:

• 
  большое количество информации, необходимой для представления объемных данных. Например, объем 256x256x256 имеет небольшую разрешающую способность, но требует свыше 16 миллионов вокселов;
  
• 
  значительные затраты памяти ограничивают разрешающую способность, точность моделирования;
  
• 
  большое количество вокселов обуславливает маленькую скорость создания изображений объемных сцен;
  
• 
  как и для любого растра, возникают проблемы при масштабировании — увеличении или уменьшении.
  

7.1.4 Равномерная сетка

Эта модель описывает координаты отдельных точек поверхности следующим способом (рис. 7.11). Каждому узлу сетки с индексами (i,j) приписывается значение высоты z_i,j. Ин­дексам (i,j) соответствуют определенные значения координат (х,у). Расстояние между уз­лами одинаковое — dx по оси х и dy по оси у.

Фактически, такая модель является двумерным массивом (растром, матри­цей), каждый элемент которой хранит значение высоты.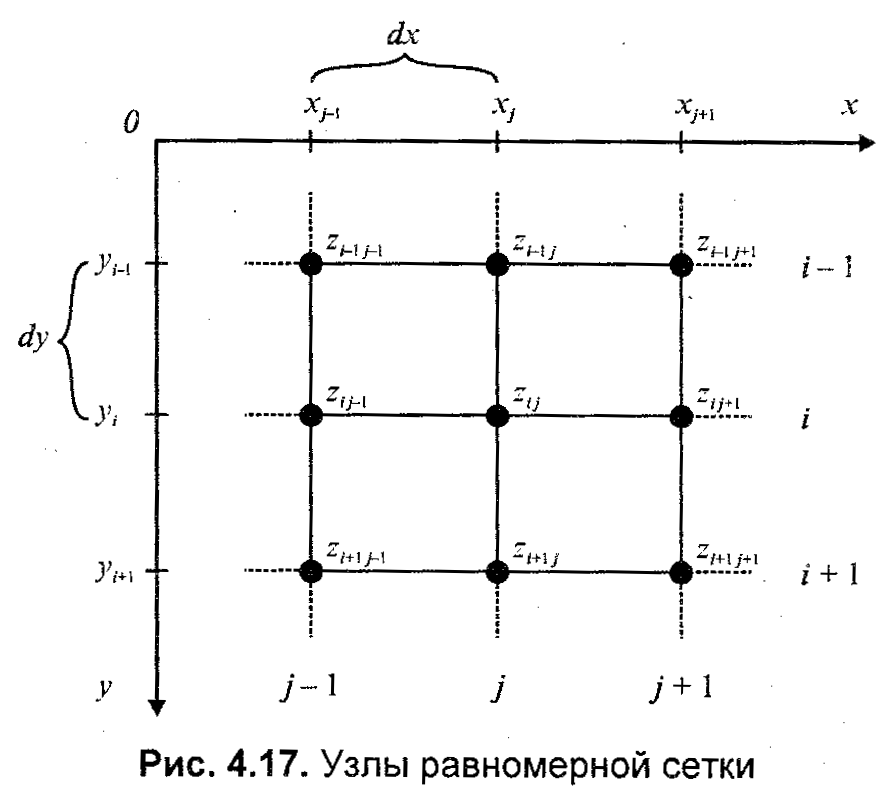



Рис. 7.11. Узлы равномерной сетки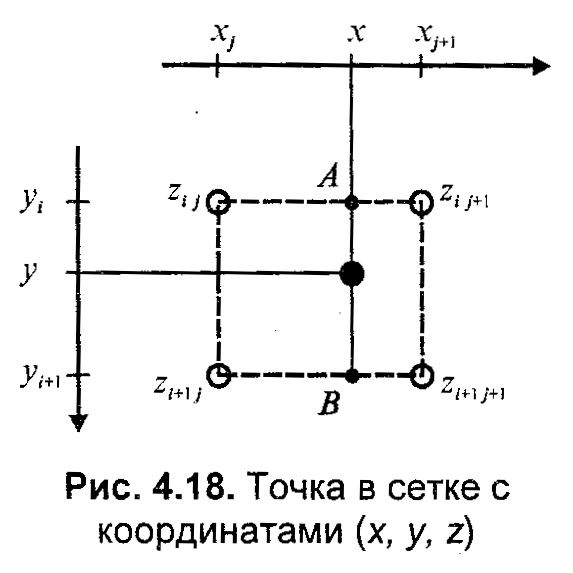


Рис. 7.12. Точка в сетке с координатами (x, y, z)
Не каждая поверхность может быть представлена этой моделью. Если в каж­дом узле записывается только одно зна­чение высоты, то это означает, что по­верхность описывается однозначной функцией z=f(xy). Иначе говоря, это такая поверхность, которую любая вер­тикаль пересекает только один раз. Не могут моделироваться также вертикаль­ные грани. Следует отметить, что для сетки не обязательно использовать толь­ко декартовы координаты. Например, для того, чтобы описать поверхность шара однозначной функцией, можно использо­вать полярные координаты. Равномерная сетка часто ис­пользуется для описания рельефа земной поверхности.

Рассмотрим, как можно рассчитать значение высоты для любой точки внутри границ сетки. Пусть ее координаты равняются (х, у). Надо найти соответствующее значение z. Решение этой задачи — интерполяция значений координат 2 ближайших узлов (рис 7.12).

Сначала необходимо вычислить индексы i и j одного из узлов:



где ]а[ — целая часть числа а, то есть наибольшее целое, которое не превышает а.

Далее используем, например, билинейную интерполяцию. Для этого сначала найдем значения г в точках А и В. Изпропорции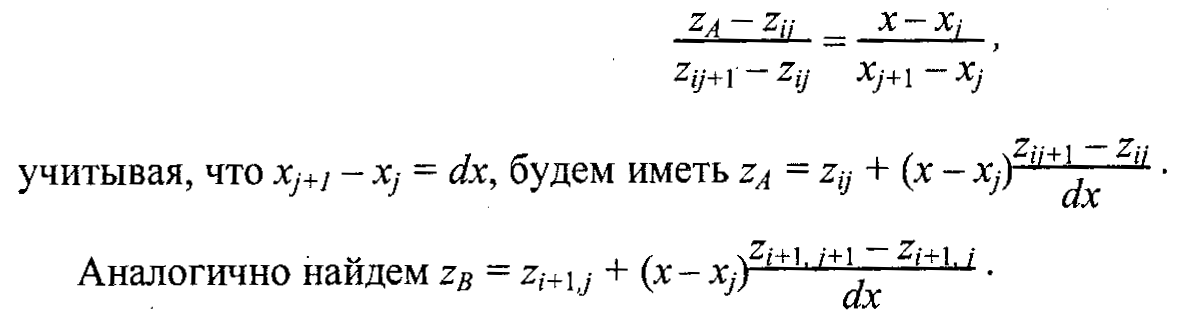




учитывая, что x_j+1 - x_j = dx, будем иметь: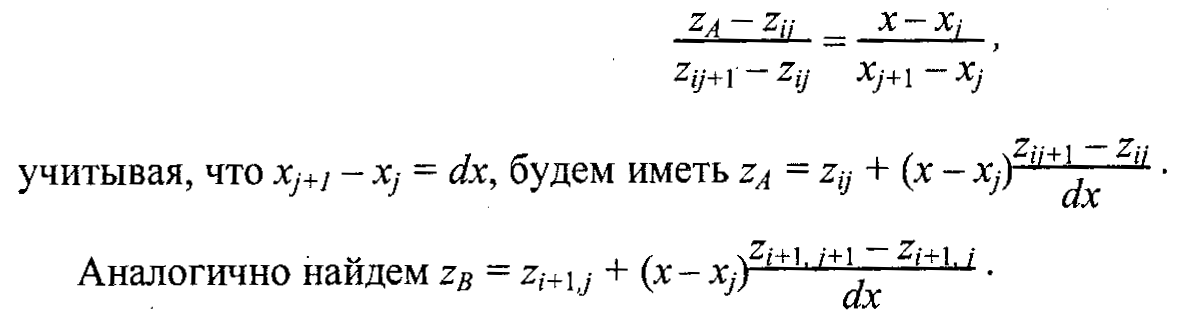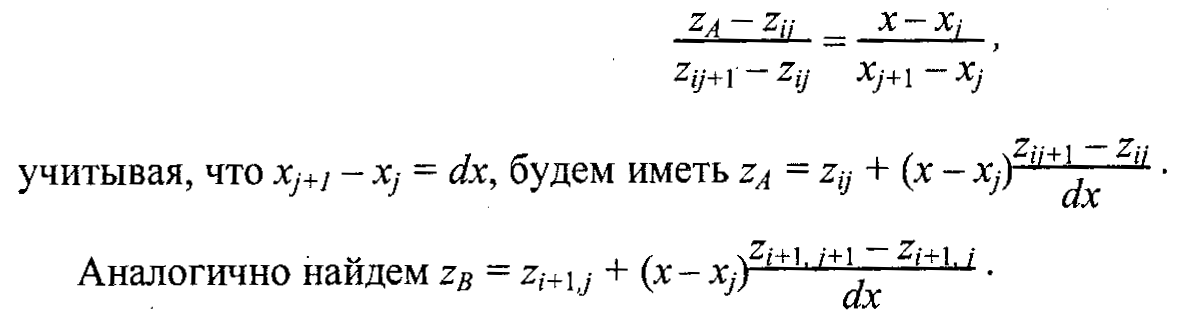






Аналогично найдем


Теперь нужно вычислить такое значение z, поделив отрезок АВ пропорционально значению у: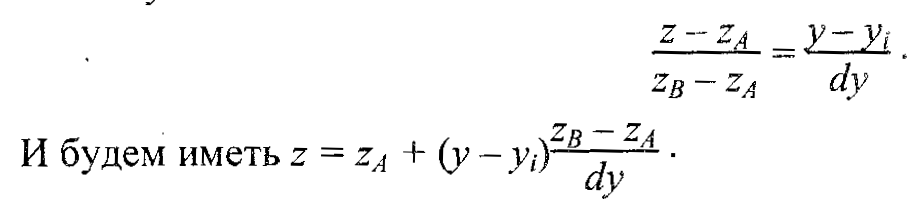



И будем иметь: z = z_А + (y – y_i)

Положительные черты равномерной сетки:

1. Простота описания поверхностей

2. Возможность быстро узнать высоту любой точи поверхности простой интерполяцией.

Недостатки равномерной сетки:

1. Поверхности, которые соответствуют неоднозначной функции высоты в узлах сетки, моделироваться не могут

2. Для описания сложных поверхностей нужно большое количество узлов, которое может быть ограничено объемом памяти компьютера

3. Описание отдельных типов поверхностей может быть более сложным, чем в других моделях. Например, многогранная поверхность требует избыточный объем данных для описания в сравнении с полигональной моделью.

7.1.5 Неравномерная сетка. Изолинии

Неравномерной сеткой назовем модель описания поверхности в виде множества отдельных точек {(х₀, у₀, z₀), (х₁, у₁, z₁), ..., (х_n-1, у_n-1, z_n-1)} принадлежащих поверхности. Эти точки могут} быть получены, например, в результате измерений поверхности какого-либо объекта с помо­щью определенного оборудования.

Такую модель можно считать обобщением для некоторых рассмотренных нами моде­лей. Например, векторная полигональная модель и равномерная сетка могут считаться раз­новидностями неравномерной сетки. Эти разновидности мы рассмотрели в отдельности, так как они играют важную роль при решении задач КГ. А вообще, может существовать не один вариант классификации способов описания поверхностей. Следует учитывать определенную условность нашего перечня моделей поверхностей, последовательность перечисления таких моделей может быть и другой.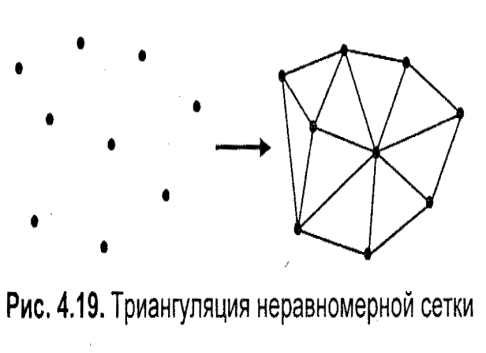


Рис. 7.13. Триангуляция неравномерной сетки
Рассмотрим модель описания поверхности в виде множества точечных значении, логически никак не связанных между собою. Неравномерность задания опорных точек усложняет определение координат для других точек поверхности, которые не совпадают с опорными точка­ми. Нужны специальные методы пространственной интерполяции. Так, например, можно поставить такую задачу - по известным координатам (х, у) вычислить значение координаты z. Для этого необходимо найти несколько ближайших точек, а потом рассчитать искомое значение, исходя из взаимного расположения этих точек в проекции (x,y). Как мы уже рассмотрели выше, для равномерной сетки это намного проще— поиска фактически нет, мы сразу вычисляем индексы ближайших опорных то­чек. Еще одна задача — отобразить поверх­ность. Эту задачу можно решать нескольки­ми способами, в том числе триангуляцией. Процесс триангуляции можно представить себе так (рис. 7.13).

Сначала находим первые три самые близкие друг другу точки — и получаем одну плоскую треугольную грань. Потом находим точку, ближайшую к этой грани, и образуем смежную грань. И так далее, пока не ос­танется ни одной отдельной точки. Это общая схема, в литературе описано много разных спо­собов триангуляции. Довольно часты ссылки на триангуляцию Делон.

Пусть нужно связать треугольниками четыре точки. Возможны два варианта триангуля­ции (рис. 7.14).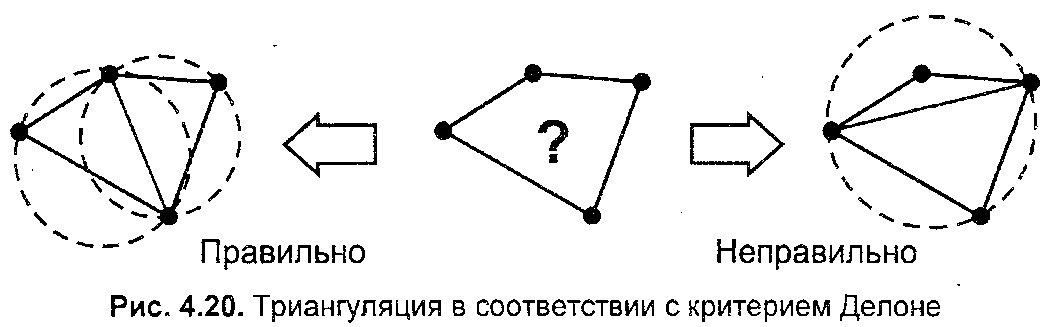

В cоответствии с критерием Делоне ни одна окружность, проходящая через три точки любого треугольника, не должна охватывать точки, которые принадлежат другим тре­угольникам. Здесь необходимо указать, что не всегда триангуляция Делоне дает нужный результат. Может так случиться, что необходимо соединять точки треугольниками вопреки указанному выше критерию. Например, кроме точек триангуляции нужно учитывать осо­бенности формы некоторых структурных элементов — горных хребтов, ям с отвесными стенами и т.п. Тогда нужно соответственно управлять триангуляцией.

Представление поверхности треугольными гранями в настоящее время очень часто ис­пользуется в разнообразных областях — от компьютерных игр и фильмов до систем авто­матизированного проектирования и ГИС. Треугольник сейчас — базовый элемент для со­временных видеоадаптеров. В англоязычной литературе для триангуляционной модели встречается и такое название: TIN (TriangulatedIrregularNetwork)

Следует заметить, что, по всей видимости, преобразование неравномерной сетки в три­ангуляционную модель в ходе визуализации нецелесообразно. Для обеспечения высокой скорости графики, например в режиме анимации, следует заранее один раз преобразовать неравномерную сетку во множество треугольников (а это по нашей классификации уже векторная полигональная модель), а затем в ходе создания кадров многократно использовать готовый результат триангуляции.

Рис. 7.14. Триангуляция в соответствии с критерием Делоне
Рассмотрим еще один из вариантов описания поверхности — изолинии высоты. Любая изолиния состоит из точек, которые представляют одно числовое значение какого-либо по­казателя, в данном случае — значение высоты (рис. 7.15). Изолинии высоты также можно представить себе как контуры разреза поверхности горизонтальными плоскостями (поэто­му для изолиний высоты часто используется название "горизонтали").

Описание поверхности изолиниями высоты часто используется, например, в картогра­фии. По бумажной карте можно с определенной точностью рассчитать высоту в точках ме­стности, углы наклона и прочие параметры рельефа. Необходимо заметить, что описание рельефа земной поверхности изолиниями высоты неправильно представлять как разрезы горизонтальными плоскостями, так как поверхность Земли не плоская. Если бы Земля была шаром, то изолинии высоты можно было бы трактовать как изолинии радиусов. Однако Земля — не шар, она имеет намного более сложную форму, названную геоидом. В геодезии и картографии геоид аппроксимируют с определенной точностью разнообразными эллипсоидами. Таким образом, здесь можно говорить об изолиниях некоторых условных высот в специальных системах координат.

Конечно, для описания поверхности можно использовать не только изолинии высоты, а также другие изолинии, например х- или у-изолинии.

В компьютерных системах изолинии часто описываются векторно — как полилинии. Используются также изолинии в виде сплайновых кривых.

Точки, которые составляют изолинии, и отдельные опорные точки располагаются нерав­номерно.


Рис. 7.15 Пример поверхности: а — изолинии высоты; б — вид поверхности; в — фрагмент триангуляционной сетки; г — поверхность из треугольников (здесь нарочно подчеркнуты отдельные треугольные грани)
Это усложняет расчет координат точек поверхности. В графических компьютерных системах для выполнения многих операций, и в первую очередь — для показа поверхности, обычно необходимо преобразовать описание поверхности в другую форму. Преобразование изолиний в полигональную модель также выполняется методами триангуляции (здесь алго­ритмы триангуляции сложнее, чем для триангуляции массива отдельных точек). Для преобра­зования неравномерной сетки в равномерную используют специальную интерполяцию.

Положительные черты неравномерной сетки: наглядность показа рельефа поверхности изолиниями на картах, планах; использование отдельных опорных точек, наиболее важных для заданной формы поверхности, обуславливает меньший объем информации по сравне­нию с другими моделями, например, с равномерной сеткой.

Недостатки неравномерной сетки: невозможность или сложность выполнения многих операций над поверхностями; сложные алгоритмы преобразования в другие формы описа­ния поверхностей.