Конспект лекций по компьютерной графике. Конспект лекций по дисциплине Компьютерная графика

• Название: Конспект лекций по дисциплине Компьютерная графика
• Анкор: Конспект лекций по компьютерной графике.doc
• Дата: 22.04.2017
• Размер: 16.3 Mb.
• Имя файла: Конспект лекций по компьютерной графике.doc
• Тип: Конспект лекций; #5372
• страница: 26 из 46

8.4. Имитация микрорельефа

Пусть нам необходимо показать поверхность, изобилующую мелкими неровностями. Можно попытаться создать полигональную модель, аппроксимирующую все видимые детали рельефа, вплоть до мельчайших бугорков, ямок, трещин и т. п. Однако это может потребовать такого количества треугольников, которое не в состоянии поддержать компьютерная система.

Для визуализации таких поверхностей часто используется следующий метод. Общие очертания поверхности моделируются полигонами, а имитация мелких деталей рельефа производится с помощью текстур.

Рассмотрим один из популярных в настоящее время методов рельефного текстурирова-ния — DOT3. Согласно этому методу, каждый тексел текстуры хранит коор­динаты вектора нормали для соответствующей точки поверхности (рис. 8.9).

Почему лучше использовать карту нормалей, а не само изображение в виде текстуры? Потому что, это дает возможность создавать иллюзию игры света и тени при смене ракурса показа и возможном движении источников света, и даже при деформациях поверхности. Обычная текстура это обеспечить не в состоянии — она представляет изображение, сделан­ное только для одного ракурса показа и фиксированного положения источников света.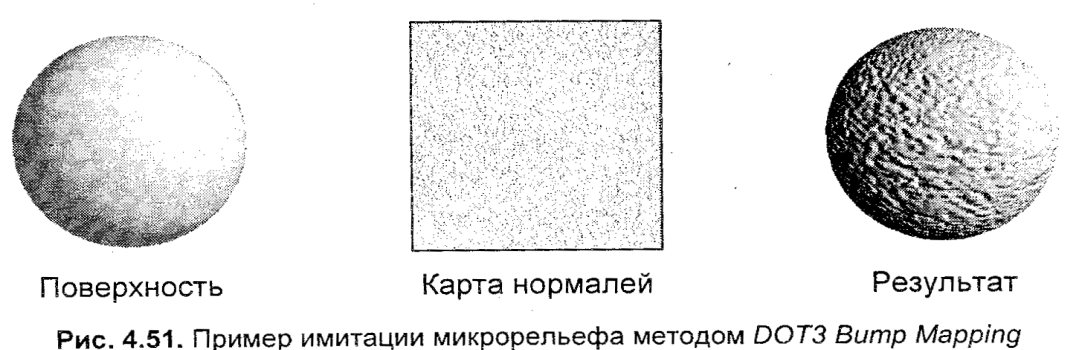




Рис. 8.9. Пимер имитации микрорельефа методом DOT3 Bump Mapping
Для хранения координат нормалей удобно использовать 24-битный растровый графиче­ский формат файлов — тут каждая тройка RGBбудет представлять тройку координат UVN. Координаты UVNописывают векторы нормалей в так называемой касательной или танген­циальной системе координат (рис. 8.10).




Рис. 8.10. Используемые системы координат

У системы координат UVNоси Uи Nлежат в плоскости текстуры, они параллельны осям текстурных координат Х_Tи Y_T, а ось N является нормалью к поверхности. Пусть задан вектор направления света L. Тогда, при расчете цвета пиксела поверхности, например, для диффузной модели отражения, можно использовать скалярное произведение векторов Lи Nbump:
Цвет точки = (собственный цвет поверхности) xDOT3(L, Nbump)
где DОТ — часто используемое в англоязычной литературе обозначение для скалярного произведения (botproduct) векторов (отсюда и название DОТЗ Витр Маррing).

Очевидно, что для корректного вычисления результата необходимо использовать в ска­лярном произведении одну и ту же систему координат для векторов L и Nbump . Для этого нужно привести вектор Nbump систему координат, описывающую вектор L(обычно это мировые координаты). А можно наоборот, выразить вектор L в системе координат UVN.
Преломление света

Законы преломления света следует учитывать при построении изображений прозрачных объектов.

Модель идеального преломления. Согласно этой модели луч отклоняется на границе двух сред, причем падающий луч, преломленный луч и нормаль лежат в одной плоскости (в этой же плоскости лежит и зеркально отраженный луч).

Обозначим угол между падающим лучом и нормалью как ₁, аугол между нормалью и преломленным лучом как ₂. Для этих углов известен закон Снеллиуса, согласно которому

n₁sin α₁ = n₂ sin α₂

где n₁иn₂ — абсолютные показатели преломлениясоответствующих сред.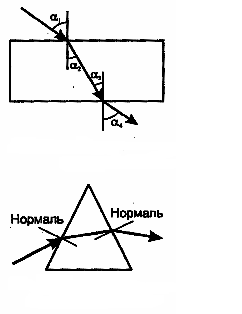



Рис. 8.11. Преломление луча и преломление в треугольной призме

На рис. 8.11 изображен пример отклонения луча при пре­ломлении. В данном случае границей раздела сред служат две параллельные плоскости (например, при прохождении луча через толстое стекло). Очевидно, что угол ₁ равняется углу ₄, а угол ₂ равняется углу ₃. Другими словами, после про­хождения сквозь стекло луч будет параллельно смещен. Это смещение зависит от толщины стекла и соотношения показа­телей преломление сред. Возможно, это простейший пример преломления. Вы, наверное, уже наблюдали и более сложные объекты, например, треугольную призму. Для нее границами сред являются непараллельные плоскости. Про­зрачные объекты могут иметь и криволинейные поверхности (например, линзы в разнообразных оптических приборах).

Принято считать, что для вакуума абсолютный показатель преломления равняется единице. Для воздуха он составляет 1.00029, для воды — 1.33, для стекла разных сортов: 1.52 (лег­кий крон), 1.65 (тяжелый крон). Показатель преломления зависит от состояния вещества, например, от температуры. На практике обычно используют отношение показателей прелом­ления двух сред (n1/п2), которое называют относительным показателем преломления.

Кроме идеального преломления, в компъютерной графике используется диффузное преломление. Соответственно этой модели, падающий луч преломляется во все стороны. Примером может служить молочное стекло, обледеневшее стекло.