Конспект лекций по компьютерной графике. Конспект лекций по дисциплине Компьютерная графика

• Название: Конспект лекций по дисциплине Компьютерная графика
• Анкор: Конспект лекций по компьютерной графике.doc
• Дата: 22.04.2017
• Размер: 16.3 Mb.
• Имя файла: Конспект лекций по компьютерной графике.doc
• Тип: Конспект лекций; #5372
• страница: 28 из 46

8.6 Анимация

В предыдущих параграфах мы рассмотрели методы и алгоритмы создания трехмерных моделей. В этом параграфе мы затронем вопросы, связанные с анимацией этих моделей.

Можно дать такое определение анимации — это создание зрительной иллюзии движения, изменения чего-то во времени.

Следует заметить, что в настоящее время существует некоторый разнобой в терминологии: наряду со словом "анимация" используется слово "видео". Значения этих слов не­сколько отличается. Термин "анимация" ранее использовался, когда говорили о "живых" ' куклах, а затем о персонажах мультфильмов. Само слово "видео" (со значением видео­фильм) начало использоваться в русском языке с появлением видеомагнитофонов. Есть по­нятие "цифровое видео", которое часто используют для обозначения движущегося изобра­жения, как правило фильма, сопровождающегося звуком. Таким образом, при создании ви­део (съемке фильма) какое-то непрерывное действие запечатлевалось на множестве фото­графий (кадров). Кроме того, термин "видео" употребляется для обозначения изображений на экране, воспринимаемых органами зрения, в противопоставление звуковой информации: различают видеоданные и аудиоданные.

Эффект анимации основан на некоторых особенностях зрения человека, а именно: след изображения сохраняется некоторое время на сетчатке глаза свойственна способность объединять быстро сменяющие друг друга изображения вединый зрительный ряд, который даёт иллюзию непрерывности

Эти особенности зрения человека были использованы при создании игрушек тауматроп (1825 г.) и зоотроп (1834 г.). Тауматроп представлял собой плоский диск с рисунками, нане­сенными на обе его стороны, а зоотроп — бумажную ленту с рисунками. При вращении этих игрушек возникала иллюзия движения.

В XX веке бурно развивалась мультипликация (традиционная анимация), средствами которой создавались рисованные двумерные фильмы.

Аналогично создаются движущиеся изображения на экранекомпьютера. Можно выделить два основных подхода к созданию компьютерной анимации: покадровый (каждый кадр с изображением движущегося объекта рисуется разработчиком) и по ключевым кадрам разработчик рисует опорные кадры, а программа рассчитывавает промежуточные кадры, помогая осуществить плавный переход - tween—из одного кадра в другой). Покадровый подход — очень трудоемкий, но дает более качественный результат. Анимация по ключевым кадрам значительно упрощает и ускоряет производство видеофильма, поэтому многие векторные редакторы имеют функцию Blend (перетекание), обеспечиваю­щую такую анимацию. Например, при создании сложной анимации для Интернета часто используется векторный редактор Macromedia Flash. Анимация во Flash построена на ис­пользовании ключевых кадров. Поддерживаются тип motion tween (без изменения формы объекта) и тип shape tween (с изменением формы — с морфингом). Могут быть анимированы многие параметры, в частности, яркость, цвет, прозрачность. Объекты могут двигаться по прямой линии или по заданному пути (motion path), с ускорением или замедлением (easy in/easy out).
Методы компьютерной анимации

Известные к настоящему времени технологии компьютерной анимации можно разделить на два такие класса: 2D - и ЗD - анимация. Несмотря на то, что результатом в обоих случаях является создание серии изображений в плоской проекции, методы 2D- и ЗD-анимация су­щественно различаются. Под 2D-анимацией обычно подразумевается перемещение, наложение в определенном порядке отдельных спрайтов. Например, на фон накладываются изо­бражения фигурок людей и животных. Для каждой движущейся фигурки заготавливается несколько картинок, изображающих персонаж в различных фазах движения. Картинка мо­жет быть небольшим растром. Тогда для правильного наложения такого спрайта на фон в прямоугольнике растра пикселы за границами контура фигурки делаются прозрачными. До недавнего времени компьютерная 2D-анимация была очень популярной в разнообразных компьютерных играх. Для ее поддержки, как правило, все видеоадаптеры аппаратно выпол­няют соответствующие базовые функции, и в первую очередь, быстрое копирование прямо­угольных фрагментов растра.

В настоящее время наблюдается переход на технологии 3D-анимации. Ее суть заключа­ется в использовании трехмерных моделей объектов пространственных сцен и их отобра­жение методами ЗD-графики.

Следует отметить, что некоторые методы, разработанные ранее для 20-анимации, сей­час успешно реализуются и в системах ЗD-анимации. Примером может служить следующий метод. Современные программы трехмерной анимации позволяют художнику-аниматору построить первоначальную сцену (ключевой кадр), передвинуть вперед указатель на вре­менной шкале, изменить первоначальную сцену (следующий ключевой кадр) и получить построенные самим компьютером промежуточные кадры. Таким образом реализуется так называемый метод анимации по ключевым кадрам. Но идеи метода анимации по ключе­вым кадрам возникли и использовались еще при создании рисованных мультфильмов, когда ведущий аниматор определял, и сам делал ключевые кадры, а другие аниматоры рисовали остальные кадры. Аналогичный по идеям метод расчета промежуточных изображений & ЗD-моделей - tweening- используется для уменьшения количество хранимых кадров (то­гда при воспроизведении анимации на экране осуществляется интерполяция «на лету» по­ложения вершин полигональной модели). Таким образом, одни и те же идеи и методы могут использовать и при традиционной, и при компьютерной 2D- или ЗD-анимации.

Рассмотрим вкратце остальные методы анимации.

Для создания иллюзии механического движения достаточно перемещать (поворачивать) одни модели относительно других моделей или относительно неподвижного фона (кстати, можно передвигать фон, оставляя модель неподвижной). Это методы, так сказать, простой анимации.

К методам простой анимации можно также отнести несложную деформацию (изменение масштаба всего предмета, неоднородное масштабирование, например, сжатие по одной оси и т. п.). Это также методы искажения объекта, связанные со смещением одной (не­скольких) вершин объекта и распространением смещения по направлению к соседним вер­шинам. При этом величина смещения является заданной функцией расстояния.

Разработана также группа методов, связанных либо с деформацией двумерной сетки,на которую помещен объект, либо с глобальной деформацией пространства,в котором задан объект. Часто используются различные модификации метода свободной дефор­мации (FFD— free-formdeformation), являющегося трехмерным расширением метода де­формации двумерной сетки. Общая идея этих методов основана на том, что художнику-аниматору проще оперировать системой локальных координат, в которую помещен иска­жаемый объект, чем вершинами этого объекта. Поэтому, после определенной художником-аниматором деформации локальной системы координат, производится пересчет координат вершин искажаемого объекта в глобальное пространство.

В современных программах, реализующих механическое движение, как правило, создают средства динамики, обеспечивающие анимацию объектов в соответствий с законами физики. Например, при расчете траекторий движений объектов учитываются влияния трения, гравитации, магнетизма и др. Художник-аниматор, работая с такими программами, может даже не создавать ключевые кадры — он задает начальное положение, физические свойства и законы взаимодействия объектов ит. п.

Наряду с методом анимации по ключевым кадрам, упомянутым выше, применяют и бо­лее изощренный метод анимации на основе событий (который не исключает и примене­ния ключевых кадров). При этом методе "событиям и считаются изменения в состоянии того или иного параметра. В качестве параметров выступают предусмотренные конкретной анимационной программой элементы сцены (формы объектов, текстуры, параметры источни­ков света, координаты камеры и т. д.). Для каждого параметра на временной шкале выделя­ется отдельная дорожка, что позволяет перемещать события вдоль временной шкалы или подвергать иным преобразованиям независимо друг от друга. При этом траектория объек­тов может быть нелинейной.

Для передачи движения "живых" объектов, которое характеризуется взаимосвязанным плавным перемещением нескольких (или всех) элементов объекта, возникает необходи­мость в сложной деформации модели. Например, если движется рука, то, как правило, слег­ка изменяются очертания плеча. При так называемой "лицевой анимации" необходимо ме­нять взаиморасположение нескольких элементов объектов. Такой объект должен описы­ваться единой моделью для того, чтобы при движении отдельных его частей, например, ру­ки, не создавались грубые переходы, стыки.

Один из методов более совершенной анимации — метод вершинной (вертексной) анимации объектов — связан с представлением объекта как цельной полигональной моде­ли (еще говорят, что он должен представлять собой одну сетку). Тогда, например, лицевая анимация выполняется путем передвижения по заданной траектории определенных вершин полигональной модели, в то время как положение остальных вершин не меняется, тем са­мым осуществляется деформация полигональной модели (деформация сетки объекта). Та­ким образом создается ряд трехмерных моделей, отображающих последовательность дви­жения "живого" объекта в различные моменты времени. Этот ряд последовательно выво­дится на экран (естественно, уже с текстурами, светом и т. п.), создавая иллюзию движения. Однако при таком методе анимации приходится хранить положение каждой вершины поли­гональной модели в каждом кадре анимации. То, что анимации моделей хранятся как бы по трехмерным кадрам, приводит к росту размера файлов пропорционально количеству кадров.

Разумеется, существуют методы, позволяющие снизить объемы хранимой информации в том чис­ле метод расчета промежуточных изображений (tweening) между изменениями объекта. В этих случаях для задания опорного кадра анимации используются наборы сеток, а между опорными кадрами положение точек и ориентация нормалей интерполируется необходи­мым образом (чаще всего линейно).

Следует заметить, что несмотря на преимущественное применение скелетной анимации (описана ниже), вершинная анимация продолжает использоваться по определенным сооб­ражениям (например, при желании уменьшить временные затраты или упростить код).

В качестве примера метода осуществления сложной деформации модели приведем морфинг(термин происходит от слова metamorphosing— проведение преобразования). Мор­финг заключается в последовательном превращении одного объекта в другой посредством перемещении по определенной траектории заданных точек (линий) одного объекта в соответствующие точки (линии) другого объекта в сочетании с наложением этих двух объектов. Хотя он представляет собой двумерный анимационный метод, некоторые его модификации успешно применяется наряду с трехмерным методом скелетной анимации, например, для реалистической анимации лица. Кроме того, проводятся довольно успешные исследования по осуществлению морфинга трехмерных объектов.

Существует два подхода к осуществлению морфинга — подход, основанный на ис­пользовании криволинейной координатной сетки, и подход, основанный на установлении соответствия между изображениями при помощи линий особенности. Так или иначе, при использовании морфинга приходится решать на интуитивном уровне, какие из областей изображения одного объекта и с какой скоростью преобразовывать в области изображения другого объекта.

Метод взвешенно-целевого морфинга достаточно успешно применяется для реалистичной анимации лица. Такое название метод получил вследствие особенности обеспечения требуемого выражения лица. В соответствии с этим методом вначале подготавливаются ключевые состояния лица: улыбка, широко раскрытые глаза, насупленные брови и т. д. Затем указываются "весовые" доли для каждого из этих ключевых состояний, тем самым создается требуемое выражение лица.

Одним из наиболее эффективных и часто применяемых является метод скелетной анимации, при котором перемещение вершин полигональной модели осуществляется с по­мощью невидимых анимированных "костей" (bones), составляющих иерархическую структуру - "скелет" (skeleton). Для каждой кости задаются длина и некоторые параметры, ха­рактеризующие ее положение.

Рассмотрим следующий пример (рис. 8.18).

Чтобы имитировать движения рыбки нужно как-то деформировать соответствующую полигональную сетку. Движения хвоста можно осуществлять простейшим способом — сдвигать координаты всех вершин пропорционально расстоянию вершины от головы. Но так невозможно имитировать поворот хвостового плавника на угол 90 градусов и более. Можно наряду с глобальным сдвигом применять локальные повороты групп вершин. Дви­жения губ и плавников можно было бы выполнить как перемещения отдельных вершин.

Однако описание соответствия указанных преобразований сетки и движений рыбки здесь представляется достаточно сложным и запутанным. Как представляется, здесь лучше использовать деформацию поверхности на основе скелетной модели. Для построения изображения рис. 8.18 мы использовали один из простейших вариантов скелета.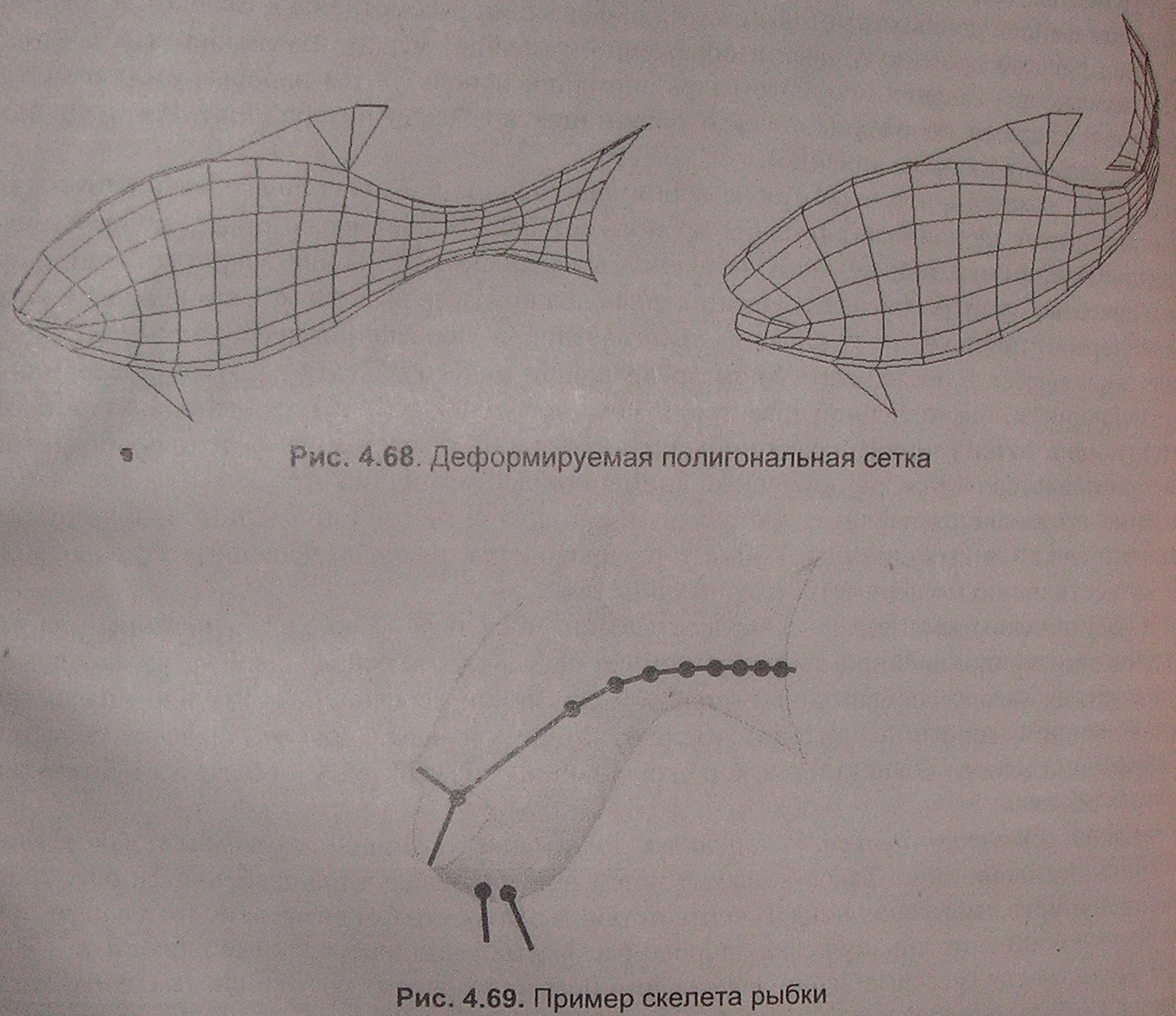


Рис. 8.18. Пример деформируемой полигональной сетки

Сложность скелета определяется требуемым уровнем детализации изображаемого объ­екта. Например, при изображении человека, шагающего где-то вдали, достаточно показать основные движения рук и ног, в то время как для крупных планов, возможно, потребуется показать движения отдельных пальцев (рис. 8.19).

Скелет состоит из костей (звеньев) и сочленений (на рис. 8.19 сочленения изображены кружочками). Каждая i-я кость описывается такими параметрами: длиной (l_i) и поворотами относительно родительской кости. Если поворот возможен только в одной плоскости, то говорят, что такое сочленение имеет одну вращательную степень свободы. Если повороты могут осуществляться в двух или трёх плоскостях, то это называют двумя или тремя степенями свободы. Заметим, что в теории манипуляторов кроме вращательных движений движений элементов шарнирных конструкций предусматривают также возможность изменения длины звена - это еще одна степень свободы. В качестве базового элемента для расчётов удобно использовать звено только с одной вращательной степенью свободы. В этом случае сочле­нение с несколькими вращательными степенями свободы представляется из нескольких со­членений звеньев нулевой длины. Таким образом, для описания каждой кости будем ис­пользовать один угол поворота (α_i).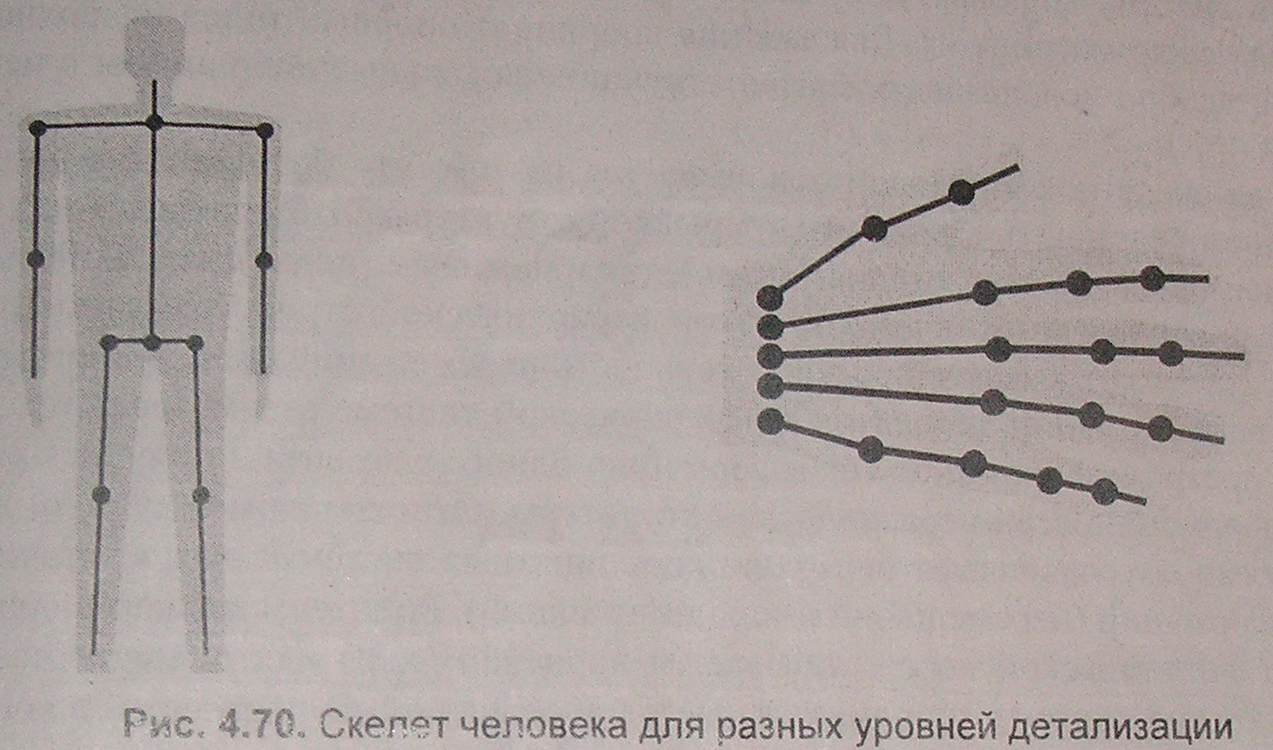




Рис. 8.19. Скелет человека для разных уровней детализации

Скелет имеет древовидную иерархическую структуру — с ро­дительской костью соединяется одна или несколько костей, ко­торые, в свою очередь могут являтьсяродительскими для других соединенных с ними костями. Рассмотрим конструкцию из двух костей (рис. 8.20).

Зафиксируем систему трехмерных координат (х₀, у₀, z₀)в на­чале родительской кости (ось у₀ смотрит на нас). Угол поворота родительской кости (α₁) здесь отсчитывается от вертикали (хотя это не принципиально).

Найдем координаты произвольной точки Р,связанной с кон­цом второй кости:
Р = R₁х T₁х R₂х Т₂ х Р₂,

где Р₂— это координаты искомой точки, заданные в локальной системе координат

(х₂, y₂, z₂),центр которой располагается в кон­це второй кости, R₁и R₂— матрицы поворотов на углы α₁и α₂, Т₁и T₂ — матрицы сдвига вдоль оси zна длину костей.

Обобщим эту формулу для шарнирного соединения пкостей.

Р = М_п* P_n,

где Р_п— это координаты искомой точки в локальной системе координат, связанной с кон­цом последней кости шарнира, М_п— матрица преобразований координат. Эту матрицу удо­бно вычислять рекурсивно:
M_i = M_i-1x R_ix T_i,

где i = 1,2, …, n, причем

M₁ = R₁x T₁.




Рис. 8.20. Взаимное расположение двух костей.

Если требуется вычислить мировые координаты всех точек поверхности (опорных точек полигональных сеток) тела движущегося объекта, то необходимо вначале определить мат­рицу преобразований из локальной системы, связанной с начальной точкой всех родительских костей, в систему мировых координат. Затем произвести обход скелета, для каждой кости вычисляя свою матрицу М_i. Для задания координат опорных точек поверхности тела вокруг костей, удобно использовать соответствующие локальные координаты с центрами в концах костей.

Идея метода скелетной анимации основывается на том, что большинство движущихся объектов можно представить в виде иерархической структуры. Это относится как к живым объектам (людям, животным, растениям и т.п.), так и неживым (планетные системы, роботы и т. п.). Перемещение одного элемента такой иерархической структуры относительно другого элемента может вызвать последовательность перемещений ряда элементов. Другими словами, трансформации элементов в иерархической системе взаимозависимы, поэтому можно задать программе анимации трансформацию одного элемента и получить рассчитан­ную ею трансформацию всей иерархической структуры. Отношения между родительской и дочерней костями обуславливают иерархию координатных систем и соответствующую ие­рархию трансформаций (перемещений и/или деформаций). Родительская кость, для которой не существует родительской кости, называется корневой (root) или предком всех других Костей, ее локальная система координат является абсолютной. В частности, для скелетной модели человека в качестве корневой кости часто выбирают тазовую кость.

Следует заметить, что в целях экономии времени расчета и объема памяти при анима­ции иногда используют простейший вариант использования скелета — каждая вершина по­лигональной сетки поверхности связывается только с одной костью. Однако лучшее качест­во, большая реалистичность достигаются при учете влияния на одну вершину нескольких костей. В этом случае для вершины задают степень влияния каждой кости с помощью ко­эффициента веса, сумма которых для одной вершины, как правило, должна быть равна единице. В соответствии со значениями этих коэффициентов выполняется интерполяция координат вершин полигонов (метод интерполяции вершин — vertexblending).

Как подмножество метода интерполяции вершин может рассматриваться vertexskinning— метод трансформации вершин геометрической сетки в местах сгиба модели. Применяется метод vertexskinningдля того, чтобы на стыках текстур (особенно на сгибах и сочлене­ниях — это, например, все суставы модели человека или животного) были плавные, естественные переходы, особенно во время движения. Таким образом, при помощи этого метода осуществляется правильное расположение вершин. Для этого используются матрицы, назы­ваемые skinningmatrices. Текстуры же на корректно трансформированную геометрию натя­гиваются правильно автоматически. Основная идея этого метода — интерполировать ре­зультаты матричного преобразования, используя веса, основанные на начальном местопо­ложении каждой вершины. Это позволяет отдельному треугольнику сетки деформироваться (натягиваться подобно коже) и сохранять связь, например, с суставами, поскольку каждой вершине приписывают различный вес.

Таким образом, вычисление координат некоторой вершины Vинтерполяцией в соответствии с методом vertexblendingможно описать так:
V= V₁x k + V₂ x (1-k),
где V₁ , V₂— используемые вершины, а коэффициент kпринимает значение в диапазоне от 0 до 1.

Метод vertex skinning - это vertex blending для вершин, обработанных разными матри­цами (М₁,М₂):

V = V₁ x M₁ x k + V₂x M₂ x (1-k).
Фирма ATI начала продвигать возможности “матричного наложения” (“matrixskinning”)в видеоадаптерах RADEON. Эта технология получила высокую оценку разработчиков, т.к. она позволяет очень реалистично "растягивать" кожу персонажей и отображать их суставы

Итак, подытожим. Для осуществления скелетной анимации какого-нибудь персонажа необходимо, прежде всего, создать его полигональную модель (сетку персонажа). Дефор­мация сетки персонажа осуществляется под влиянием скелета. Он создается и подгоняется под размеры и форму тела персонажа, затем каждая вершина сетки связывается с одной или несколькими костями скелета. Если какая-то кость подверглась трансформации, то необхо­димо выполнить расчет скелета, вследствие чего осуществляется деформация сетки. Иными словами, при анимации изменяются параметры положения частей скелета, а сетка лишь следует за ними.

Основные достоинства метода скелетной анимации заключаются в следующем:

• 
  в меньшем размере файлов, в которых хранится анимация, так как в них нет необхо­димости хранить положения всех вершин для всех кадров;
  
• 
  в лучшем качестве изображения по сравнению с вершинной анимацией при том же (и даже меньшем) количестве полигонов;
  
• 
  в упрощении задач художника-аниматора, так как ему не нужно самому отслеживать трансформацию по всей иерархии костей.
  

Одной из проблем реализации метода скелетной анимации является управление движе­нием костей скелета. Нужно как-то описывать последовательность движений костей, соот­ветствующих требуемым движениям персонажа. Пусть, например, у персонажа таз — это корневое звено, для которого туловище и ноги являются дочерними звеньями. В свою оче­редь, ноги являются родительскими звеньями по отношению к ступням.

В соответствии с методом прямой кинематики (ForwardKinematics) управляя углами поворота костей скелета, добиваются требуемых поз. Процесс подбора углов можно представить следующим образом. Движение родительского звена (например, ноги) автоматиче­ски приводит в движение всю цепь дочерних звеньев (в данном случае ступню), причем до­черние звенья будут перемещаться, не изменяя своего положения относительно объекта-предка. Если родительское, звено поворачивается, то дочернее соответственно и перемеща­ется, и поворачивается, чтобы его ориентация по отношению к родительскому звену оста­лось прежней. Этот метод несколько утомителен для художника-аниматора, так как требует указывать множество углов в сочленениях.

При использовании метода обратной (инверсной) кинематики (InverseKinematics) исходными являются позы, а точнее, координаты концевых точек звеньев скелета. Исходя из этих координат, находятся соответствующие углы поворота всех костей. Движение задается перемещением самого младшего дочернего звена (в нашем случае ступни), что застав­ляет всю остальную цепочку (ногу, туловище, таз и т.д.) перемещаться. Как правило, расчет перемещений осуществляется с учетом ограничений на работу сочленений звеньев: напри­мер, вводятся приоритеты сочленений, их фиксация, угловые ограничения и трение в узлах сочленений и т.п. При этом метод обратной кинематики, в отличии от метода прямой кине­матики, может дать несколько вариантов решения (или странные и непредвиденные решения) — это зависит от количества звеньев и ограничений. На рис. 8.21 показано, что даже для простейшего скелета из двух костей могут быть два варианта их углов поворота.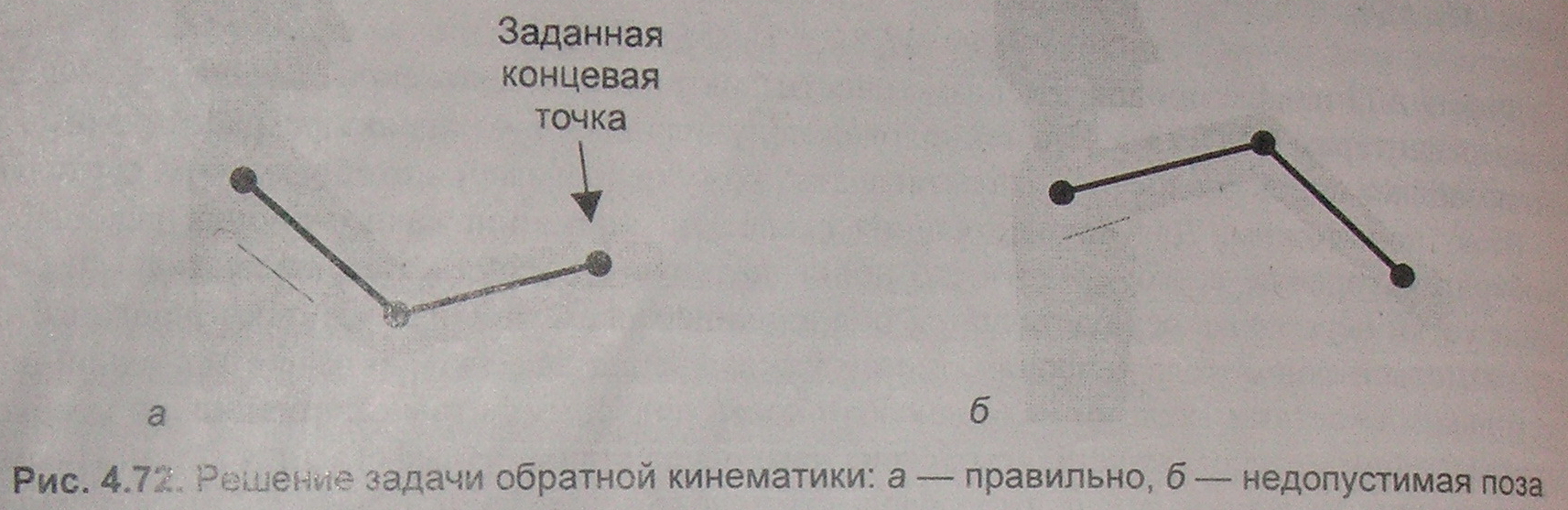



Рис. 8.21. Решение задачи обратной кинематики: а – правильное, б - неправильное
Задача обратной кинематики для простых скелетов с небольшим количеством звеньев может решаться аналитически непосредственно. Для расчета сложных скелетных конструк­ции применяются математический аппарат якобианов и соответствующие итерационные методы.

Следует отметить, что при использовании, например, метода обратной кинематики рас­чет скелета может не производиться заранее, а вычисляться процедурно. Так называемый метод процедурной анимации применяется в тех случаях, когда моделирования движений трудно (неэффективно) воспроизводить с помощью ключевых кадров. При процедурной анимации текущие значения параметров анимации рассчитываются на основе заданных начальных значений и математических выражений, описывающих изменение параметров во времени. Процедурная анимация часто используется для качественной анимации разнооб­разных физических эффектов.

Аналогично применяется параметрическая анимация. Вроли параметра может высту­пать любой объект — кривая, поверхность, точка, систем координат и т.д. Например, часто­ту или скорость движения объекта можно задать графиком, а затем анимировать этот гра­фик, изменяя тем самым параметры движения объекта.

Упомянем также о таких средствах анимации как редактирование кривых действия и системы частиц (particle systems).

Движения, особенно "живых" объектов в реальном мире редко бывает линейным: на­пример, объекты могут плавно замедлять ход, а затем резко останавливаться. Для подго­товки подобных эффектов используются графические средства редактирования кривых действия.

При использовании метода моделирования частиц (particles) создается набор частиц (часто в качестве частиц используются точки, то есть объекты, не имеющие размеров). Для частиц могут быть заданы законы их существования, например, основанные на каких-то реальных физических законах, а именно, законах притяжения под действием силы тяжести, электростатических, магнитных сил, и т.п.

Например, система частиц в разработанной компанией RealSoft OY системе 3D-графики RealSoft 4D может работать с частицами следующих типов: 1D, 2D, 3D, NURBS-кривые (NURBS — Non Uniform Rational B-Spline -неоднородный рациональный Би-сплайн), причем любой объект сцены может быть представлен как частица. Частицы рассчитываются как брызги воды, туман,огонь, они могут использоваться в качестве параметров для процедурной обработки. Любая поверхность может быть источником частиц, и любой объект может быть ими заполнен. При движении частицы могут быть заданы начальные параметры ее движения, действующие на нее силы, время жизни, цветовые параметры и т.п. Частицы могут быть текстурированы, все атрибуты частиц (например, толщина, длина или прозрач­ность) доступны для анимации. Комбинируя все эти возможности моделирования, худож­ник может создать модели персонажей, декорации и окружающую среду.

Кроме того, в состав RealSoft 4D входит Envelope System — редактор графов, с помощью которого можно управлять поведением любого атрибута объекта в виде функции другого ат­рибута объекта сцены. Например, можно задать закон изменения угла скелетона в зависимо­сти от гравитационного поля. Графы представлены как NURBS-кривые в 4D- пространстве, что позволяет получать очень мягкие движения при анимации

Методы обратной кинематики и анимации по ключевым кадрам используются совмест­но с методом канальной анимации. Метод канальной анимации (channelanimation) осно­ван на снятии информации о каком-либо параметру объекта с датчика (канала). Например, для снятия информации о движении актера датчики крепятся по всему его телу в тех мес­тах, которые будут приведены в соответствие с контрольными точками компьютерной мо­дели для ввода и оцифровки движения, а приемники информации подключены к компьюте­ру. Датчики могут быть разных видов, например, электромеханическими, электромагнитными (беспроводными или соединяющимися с компьютером проводами) или оптико-электронными, информацию с которых считывают специальные оптические устройства, подключенные к компьютеру. Следует заметить, что в настоящее время беспроводные дат­чики используются реже, так как для снабжения их энергией актеру приходится носить на себе аккумулятор. Оцифрованные движения реального человека служат для создания моделей, изображающих компьютерный персонаж.

На этом методе основано относительно новое направление в анимации — технология realtimeperformanceanimation, основанная на захвате (видеозахвате) движения (MotionCapture), который дает возможность передавать естественные, реалистичные движения в реальном времени. Для захвата движений часто используют пассивные оптические метки и видеотехнологию для записи движений объекта. В этом случае актеру приходится носить только отражающие свет метки, закрепленные на одежде. Естественно, что качество синте­зированного движения напрямую зависит от количества и расположения датчиков.

Таким образом могут создаваться данные для библиотеки движений, в которых содержится информация о движении тех или иных частей тела человека, животного при конкретных дейст­виях. Использование библиотеки значительно упрощает и удешевляет создание анимации.