|
|
шгдш. 3.2 Конспект лекций ЗИвТС. Конспект лекций по курсу Защита информации в телекоммуникационных системах Буя П. М. Тема 1 Основные понятия и терминология защиты информации 1 Основные понятия
6.5 Электронная цифровая подпись
При обмене электронными документами по сети связи возникает проблема аутентификации автора документа и самого документа, т. е. установления подлинности автора и отсутствия изменений в полученном документе. В обычной (бумажной) информатике эти проблемы решаются за счет того, что информация в документе и рукописная подпись автора жестко связаны с физическим носителем (бумагой). В электронных документах на машинных носителях такой связи нет.
Электронная цифровая подпись (ЭЦП) используется для аутентификации текстов, передаваемых по телекоммуникационным каналам. Функционально она аналогична обычной рукописной подписи и обладает ее основными достоинствами:
удостоверяет, что подписанный текст исходит от лица, поставившего подпись;
не дает самому этому лицу возможности отказаться от обязательств, связанных с подписанным текстом;
гарантирует целостность подписанного текста.
Цифровая подпись представляет собой относительно небольшое количество дополнительной цифровой информации, передаваемой вместе с подписываемым текстом. Система ЭЦП включает две процедуры: 1) постановки подписи; 2) проверки подписи. В процедуре постановки подписи используется секретный ключ отправителя сообщения, в процедуре проверки подписи – открытый ключ отправителя.
При формировании ЭЦП отправитель прежде всего вычисляет хэш-функцию h(M) подписываемого текста M. Вычисленное значение хэш-функции h(M) представляет собой один короткий блок информации m, характеризующий весь текст M в целом.
Затем число m шифруется секретным ключом отправителя. Получаемая при этом пара чисел представляет собой ЭЦП для данного текста M.
При проверке ЭЦП получатель сообщения снова вычисляет хэш-функцию m = h(M) принятого по каналу сообщения M, после чего при помощи открытого ключа отправителя проверяет, соответствует ли полученная подпись вычисленному значению m хэш-функции.
Принципиальным моментом в системе ЭЦП является невозможность подделки ЭЦП пользователя без знания его секретного ключа подписывания. В качестве подписываемого документа может быть использован любой файл. Подписанный файл создается из неподписанного путем добавления в него одной или более электронных подписей. Каждая подпись содержит следующую информацию:
дату подписи;
срок окончания действия ключа данной подписи;
информацию о лице, подписавшем файл (Ф.И.О., должность, краткое наименование фирмы);
идентификатор подписавшего (имя открытого ключа);
собственно цифровую подпись.
Технология применения системы ЭЦП предполагает наличие сети абонентов, посылающих друг другу подписанные электронные документы. Для каждого абонента генерируется пара ключей: секретный и открытый. Секретный ключ хранится абонентом в тайне и используется им для формирования ЭЦП. Открытый ключ известен всем другим пользователям и предназначен для проверки ЭЦП получателем подписанного электронного документа. Иначе говоря, открытый ключ является необходимым инструментом, позволяющим проверить подлинность электронного документа и автора подписи. Открытый ключ не позволяет вычислить секретный ключ.
Для генерации пары ключей (секретного и открытого) в алгоритмах ЭЦП, как и в асимметричных системах шифрования, используются разные математические схемы, основанные на применении однонаправленных функций. Эти схемы разделяются на две группы. В основе такого разделения лежат известные сложные вычислительные задачи:
факторизации (разложения на множители) больших целых чисел;
дискретного логарифмирования.
Алгоритм электронной цифровой подписи RSA. Первой и наиболее известной во всем мире конкретной системой ЭЦП стала система RSA. Согласно этому алгоритму, сначала необходимо вычислить пару ключей (секретный ключ и открытый ключ). Для этого отправитель (автор) электронных документов вычисляет два больших простых числа – P и Q, затем находит их произведение N = PQ и значение функции (N) = (P – 1)(Q – 1). Далее отправитель вычисляет число E из условий: E (N), НОД[E, (N)] = 1 и число D из условий: D < N, ED 1 [mod (N)]. Пара чисел (E, N) является открытым ключом. Эту пару чисел автор передает партнерам по переписке для проверки его цифровых подписей. Число D сохраняется автором как секретный ключ для подписывания.
Допустим, что отправитель хочет подписать сообщение M перед его отправкой. Сначала сообщение M (блок информации, файл, таблица) сжимают с помощью хэш-функции h(M) в целое число m: m = h(M). Затем вычисляют цифровую подпись S под электронным документом M, используя хэш-значение m и секретный ключ D: S = mD (mod N).
Пара (M, S) передается партнеру-получателю как электронный документ M, подписанный цифровой подписью S, причем подпись S сформирована обладателем секретного ключа D.
После приема пары (M, S) получатель вычисляет хэш-значение сообщения M двумя разными способами. Прежде всего он восстанавливает хэш-значение m΄, применяя криптографическое преобразование подписи S с использованием открытого ключа E: m΄ = SE (mod N). Кроме того, он находит результат хэширования принятого сообщения M с помощью такой же хэш-функции h(M): m = h(M).
Если соблюдается равенство вычисленных значений, т. е. SE (mod N) = = h(M), то получатель признает пару (M, S) подлинной. Доказано, что только обладатель секретного ключа D может сформировать цифровую подпись S по документу M, а определить секретное число D по открытому числу E не легче, чем разложить модуль N на множители. Кроме того, можно строго математически доказать, что результат проверки цифровой подписи S будет положительным только в том случае, если при вычислении S был использован секретный ключ D, соответствующий открытому ключу E. Поэтому открытый ключ E иногда называют "идентификатором" подписавшего.
К недостаткам алгоритма электронной цифровой подписи RSA можно отнести следующее:
1 При вычислении модуля N, ключей E и D для системы цифровой подписи RSA необходимо проверять большое количество дополнительных условий, что сделать практически трудно. Невыполнение любого из этих условий делает возможным фальсификацию цифровой подписи со стороны того, кто обнаружит такое невыполнение. При подписании важных документов нельзя допускать такую возможность даже теоретически.
2 Для обеспечения криптостойкости цифровой подписи RSA по отношению к попыткам фальсификации на уровне, например, национального стандарта США шифрования информации (алгоритм DES), т. е. 1018, необходимо использовать при вычислениях N, D и E целые числа не менее 2512 (или около 10154) каждое, что требует больших вычислительных затрат, превышающих на 20–30 % вычислительные затраты других алгоритмов цифровой подписи при сохранении того же уровня криптостойкости.
3 Цифровая подпись RSA уязвима к так называемой мультипликативной атаке. Иначе говоря, алгоритм цифровой подписи RSA позволяет противнику без знания секретного ключа D сформировать подписи под теми документами, у которых результат хэширования можно вычислить как произведение результатов хэширования уже подписанных документов.
Алгоритм электронной цифровой подписи Эль Гамаля (EGSA). Название EGSA происходит от слов El Gamal Signature Algorithm (алгоритм цифровой подписи Эль Гамаля). Идея EGSA основана на том, что для обоснования практической невозможности фальсификации цифровой подписи может быть использована более сложная вычислительная задача, чем разложение на множители большого целого числа, – задача дискретного логарифмирования. Кроме того, Эль Гамалю удалось избежать явной слабости алгоритма цифровой подписи RSA, связанной с возможностью подделки цифровой подписи под некоторыми сообщениями без определения секретного ключа.
Для того чтобы генерировать пару ключей (открытый ключ – секретный ключ), сначала выбирают некоторое большое простое целое число P и большое целое число G, причем G < P. Отправитель и получатель подписанного документа используют при вычислениях одинаковые большие целые числа P (
10308 или
21024) и G (
10154 или
2512), которые не являются секретными.
Отправитель выбирает случайное целое число X, 1< X (P – 1) и вычисляет Y = GX mod P. Число Y является открытым ключом, используемым для проверки подписи отправителя. Число Y открыто передается всем потенциальным получателям документов. Число X является секретным ключом отправителя для подписывания документов и должно храниться в секрете.
Для того чтобы подписать сообщение M, сначала отправитель хэширует его с помощью хэш-функции h() в целое число m: m = h(M), 1< m < (P – 1) и генерирует случайное целое число K, 1< K < (P – 1) такое, что K и (P – 1) являются взаимно простыми. Затем отправитель вычисляет целое число a: a = = GK mod P и, применяя расширенный алгоритм Евклида, вычисляет с помощью секретного ключа X целое число b из уравнения m = Xa + Kb (mod (P – 1)).
Пара чисел (a, b) образует цифровую подпись S, проставляемую под документом M. Тройка чисел (M, a, b) передается получателю, в то время как пара чисел (X, K) держится в секрете.
После приема подписанного сообщения (M, a, b) получатель должен проверить, соответствует ли подпись S = (a, b) сообщению M. Для этого получатель сначала вычисляет по принятому сообщению M число m = h(M), т. е. хэширует принятое сообщение.
Затем получатель вычисляет значение A = Ya ab (mod P) и признает сообщение M подлинным, если A = Gm (mod P). Иначе говоря, получатель проверяет справедливость соотношения Ya ab (mod P) = Gm (mod P).
Схема цифровой подписи Эль Гамаля имеет ряд преимуществ по сравнению со схемой цифровой подписи RSA:
1 При заданном уровне стойкости алгоритма цифровой подписи целые числа, участвующие в вычислениях, имеют запись на 25 % короче, что уменьшает сложность вычислений почти в два раза и позволяет заметно сократить объем используемой памяти.
2 При выборе модуля P достаточно проверить, что это число является простым и что у числа (P – 1) имеется большой простой множитель (т. е. всего два достаточно просто проверяемых условия).
3 Процедура формирования подписи по схеме Эль Гамаля не позволяет вычислять цифровые подписи под новыми сообщениями без знания секретного ключа (как в RSA).
Однако алгоритм цифровой подписи Эль Гамаля имеет и некоторые недостатки по сравнению со схемой подписи RSA. В частности, длина цифровой подписи получается в 1,5 раза больше, что, в свою очередь, увеличивает время ее вычисления.
Российский стандарт электронной цифровой подписи. В российском алгоритме цифровой подписи, определяемом стандартом ГОСТ Р 34.10-94, используются следующие параметры:
p – большое простое число длиной от 509 до 512 либо от 1020 до 1024 бит;
q – простой сомножитель числа (p – 1), имеющий длину от 254 до 256 бит;
a – любое число, меньшее (p – 1), причем такое, что aq mod p = 1;
x – некоторое число, меньшее q;
y = aх mod p.
Кроме того, этот алгоритм использует однонаправленную хэш-функцию h(M). Стандарт ГОСТ Р 34.11-94 определяет хэш-функцию, основанную на использовании стандартного симметричного алгоритма ГОСТ 28147-89.
Первые три параметра p, q и a являются открытыми и могут быть общими для всех пользователей сети. Число x является секретным ключом. Число y является открытым ключом.
Чтобы подписать некоторое сообщение m, а затем проверить подпись, выполняются следующие шаги:
1 Пользователь A генерирует случайное число k, причем k < q.
2 Пользователь А вычисляет значения r = (ak mod p) mod q, s = {xr + k [h(m)]} mod q.
Если h(m) mod q = 0, то значение h(m) mod q принимают равным единице. Если r = 0, то выбирают другое значение k и начинают снова.
Цифровая подпись представляет собой два числа: r mod 2256 и s mod 2256.
Пользователь А отправляет эти числа пользователю В.
3 Пользователь В проверяет полученную подпись, вычисляя последовательно величины v = h(m)q–2 mod q, z1 = (sv) mod q, z2 = ((q – r)v) mod q, u = (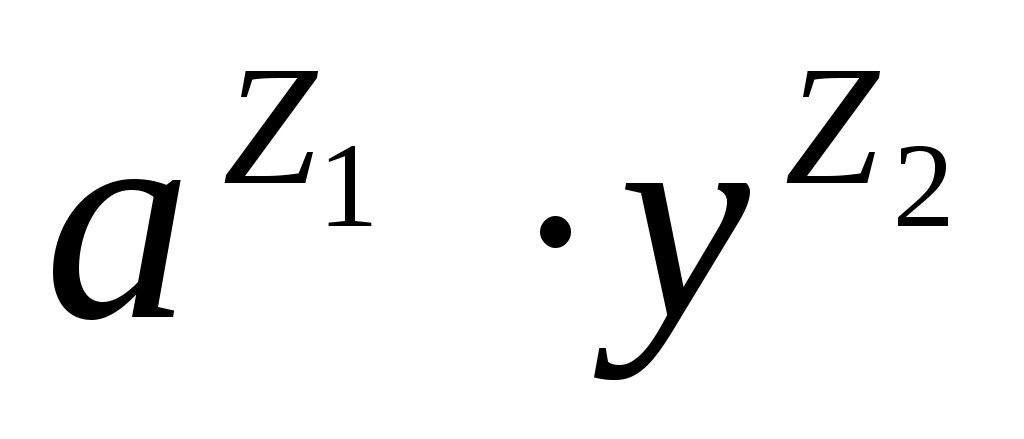 mod p) mod q. mod p) mod q.
Если u = r, то подпись считается верной.
Следует также отметить, что в данном стандарте ЭЦП параметр q имеет длину 256 бит. Западных криптографов вполне устраивает q длиной примерно 160 бит. Различие в значениях параметра q является отражением стремления разработчиков российского стандарта к получению более безопасной подписи.
6.6 Управление криптографическими ключами: генерация, хранение и распределение ключей
Как бы ни была сложна и надежна сама криптосистема, она основана на использовании ключей. Если для обеспечения конфиденциального обмена информацией между двумя пользователями процесс обмена ключами тривиален, то в системе, где количество пользователей составляет десятки и сотни управление ключами, – это серьезная проблема.
Под ключевой информацией понимается совокупность всех действующих в системе ключей. Если не обеспечено достаточно надежное управление ключевой информацией, то, завладев ею, злоумышленник получает неограниченный доступ ко всей информации.
Управление ключами – информационный процесс, включающий в себя три элемента:
генерацию ключей;
накопление ключей;
распределение ключей.
Генерация ключей. В реальных системах используются специальные аппаратные и программные методы генерации случайных ключей. Как правило используют датчики случайных чисел. Однако степень случайности их генерации должна быть достаточно высокой. Идеальными генераторами являются устройства на основе “натуральных” случайных процессов. Например, генерация ключей на основе белого радиошума. Другим случайным математическим объектом являются десятичные знаки иррациональных чисел, например или е, которые вычисляются с помощью стандартных математических методов.
В системах со средними требованиями защищенности вполне приемлемы программные генераторы ключей, которые вычисляют случайные числа как сложную функцию от текущего времени и (или) числа, введенного пользователем.
Накопление ключей. Под накоплением ключей понимается организация их хранения, учета и удаления.
Поскольку ключ является самым привлекательным для злоумышленника объектом, открывающим ему путь к конфиденциальной информации, то вопросам накопления ключей следует уделять особое внимание.
Секретные ключи никогда не должны записываться в явном виде на носителе, который может быть считан или скопирован.
В достаточно сложной системе один пользователь может работать с большим объемом ключевой информации, и иногда даже возникает необходимость организации минибаз данных по ключевой информации. Такие базы данных отвечают за принятие, хранение, учет и удаление используемых ключей.
Каждая информация об используемых ключах должна храниться в зашифрованном виде. Ключи, зашифровывающие ключевую информацию называются мастер-ключами. Желательно, чтобы мастер-ключи каждый пользователь знал наизусть и не хранил их вообще на каких-либо материальных носителях.
Очень важным условием безопасности информации является периодическое обновление ключевой информации в системе. При этом переназначаться должны как обычные ключи, так и мастер-ключи. В особо ответственных системах обновление ключевой информации необходимо производить ежедневно.
Вопрос обновления ключевой информации связан и с третьим элементом управления ключами – распределением ключей.
Распределение ключей. Распределение ключей – самый ответственный процесс в управлении ключами. К нему предъявляются два требования:
оперативность и точность распределения;
скрытность распределяемых ключей.
В последнее время заметен сдвиг в сторону использования криптосистем с открытым ключом, в которых проблема распределения ключей отпадает. Тем не менее распределение ключевой информации в системе требует новых эффективных решений.
Распределение ключей между пользователями реализуются двумя разными подходами:
1 Путем создания одного или нескольких центров распределения ключей. Недостаток такого подхода состоит в том, что в центре распределения известно, кому и какие ключи назначены, и это позволяет читать все сообщения, циркулирующие в системе. Возможные злоупотребления существенно влияют на защиту.
2 Прямой обмен ключами между пользователями системы. В этом случае проблема состоит в том, чтобы надежно удостоверить подлинность субъектов.
В обоих случаях должна быть гарантирована подлинность сеанса связи. Это можно обеспечить двумя способами:
1 Механизм запроса-ответа, который состоит в следующем. Если пользователь А желает быть уверенным, что сообщения, которые он получает от пользователя В, не являются ложными, он включает в посылаемое для В сообщение непредсказуемый элемент (запрос). При ответе пользователь В должен выполнить некоторую операцию над этим элементом (например, добавить 1). Это невозможно осуществить заранее, так как не известно, какое случайное число придет в запросе. После получения ответа с результатами действий пользователь А может быть уверен, что сеанс является подлинным. Недостатком этого метода является возможность установления, хотя и сложной, закономерности между запросом и ответом.
2 Механизм отметки времени. Он подразумевает фиксацию времени для каждого сообщения. В этом случае каждый пользователь системы может знать, насколько “старым” является пришедшее сообщение.
В обоих случаях следует использовать шифрование, чтобы быть уверенным, что ответ послан не злоумышленником и штемпель отметки времени не изменен.
При использовании отметок времени встает проблема допустимого временнόго интервала задержки для подтверждения подлинности сеанса. Ведь сообщение с отметкой времени в принципе не может быть передано мгновенно. Кроме этого, компьютерные часы получателя и отправителя не могут быть абсолютно синхронизированы.
Для обмена ключами можно использовать криптосистемы с открытым ключом, используя тот же алгоритм RSA.
Но весьма эффективным оказался алгоритм Диффи-Хелмана, позволяющий двум пользователям без посредников обменяться ключом, который может быть использован затем для симметричного шифрования.
|
|
|
 Скачать 1.52 Mb.
Скачать 1.52 Mb.