шгдш. 3.2 Конспект лекций ЗИвТС. Конспект лекций по курсу Защита информации в телекоммуникационных системах Буя П. М. Тема 1 Основные понятия и терминология защиты информации 1 Основные понятия
 Скачать 1.52 Mb. Скачать 1.52 Mb.
|
|
Аффинная система подстановок Цезаря. В данном преобразовании буква, соответствующая числу t, заменяeтся на букву, соответствующую числовому значению (at + b) по модулю m. Такое преобразование является взаимно однозначным отображением на алфавите тогда и только тогда, когда НОД (a, m) наибольший общий делитель чисел a и m равен единице, т. e. если a и m взаимно простые числа. Достоинством аффинной системы является удобное управление ключами: ключи шифрования и дешифрования представляются в компактной форме в виде пары чисел (a, b). Недостатки аффинной системы аналогичны недостаткам системы шифрования Цезаря. На практике аффинная система использовалась несколько веков назад. Шифры сложной замены. Шифры сложной замены называют многоалфавитными, так как для шифрования каждого символа исходного сообщения применяют свой шифр простой замены. Многоалфавитная подстановка последовательно и циклически меняет используемые алфавиты. При r-алфавитной подстановке символ x0 исходного сообщения заменяется символом y0 из алфавита B0, символ x1 – символом y1 из алфавита B1, и т. д.; символ xr–1 заменяется символом yr–1 из алфавита Br–1, символ xr заменяется символом yr снова из алфавита B0, и т. д. Эффект использования многоалфавитной подстановки заключается в том, что обеспечивается маскировка естественной статистики исходного языка, так как конкретный символ из исходного алфавита A может быть преобразован в несколько различных символов шифровальных алфавитов Bj. Степень обеспечиваемой защиты теоретически пропорциональна длине периода r в последовательности используемых алфавитов Bj. Система шифрования Вижинера. Система Вижинера подобна такой системе шифрования Цезаря, у которой ключ подстановки меняется от буквы к букве. Этот шифр многоалфавитной замены можно описать таблицей шифрования, называемой таблицей (квадратом) Вижинера. Таблица Вижинера используется как для шифрования, так и для расшифрования. Она имеет два входа: верхнюю строку подчеркнутых символов, используемую для считывания очередной буквы исходного открытого текста; крайний левый столбец ключа. Последовательность ключей обычно получают из числовых значений букв ключевого слова. При шифровании исходного сообщения его выписывают в строку, а под ним записывают ключевое слово (или фразу). Если ключ оказался короче сообщения, то его циклически повторяют. В процессе шифрования находят в верхней строке таблицы очередную букву исходного текста и в левом столбце очередное значение ключа. Очередная буква шифротекста находится на пересечении столбца, определяемого шифруемой буквой, и строки, определяемой числовым значением ключа. Одноразовые шифры. Почти все применяемые на практике шифры характеризуются как условно надежные, поскольку они могут быть в принципе раскрыты при наличии неограниченных вычислительных возможностей. Абсолютно надежные шифры нельзя разрушить даже при использовании неограниченных вычислительных возможностей. Существует единственный такой шифр, применяемый на практике, – одноразовая система шифрования. Характерной особенностью одноразовой системы шифрования является одноразовое использование ключевой последовательности. Этот шифр абсолютно надежен, если набор ключей Ki действительно случаен и непредсказуем. Если криптоаналитик попытается использовать для заданного шифротекста все возможные наборы ключей и восстановить все возможные варианты исходного текста, то они все окажутся равновероятными. Не существует способа выбрать исходный текст, который был действительно послан. Теоретически доказано, что одноразовые системы являются недешифрируемыми системами, поскольку их шифротекст не содержит достаточной информации для восстановления открытого текста. Возможности применения одноразовой системы ограничены чисто практическими аспектами. Существенным моментом является требование одноразового использования случайной ключевой последовательности. Ключевая последовательность с длиной, не меньшей длины сообщения, должна передаваться получателю сообщения заранее или отдельно по некоторому секретному каналу. Такое требование практически сложно осуществимо для современных систем обработки информации, где требуется шифровать многие миллионы символов, однако в обоснованных случаях построение систем с одноразовыми шифрами является наиболее целесообразным. Исторически различают шифраторы с внешней и внутренней гаммами. В шифраторах с внешней гаммой в качестве ключа используется случайная последовательность однократного использования, длина которой равна длине шифруемого сообщения. В шифраторах с внутренней гаммой в качестве ключа применяется многократно используемая случайная последовательность длиной, много меньшей длины шифруемого текста, на основе которой формируется гамма шифра. Шифраторы с внутренней гаммой, т. е. обладающие свойством практической стойкости, в настоящее время являются преобладающими при построении систем шифрованной связи. Основным их достоинством является простота в управлении ключами, т. е. их заготовка, распределение, доставка и уничтожение. Данное преимущество позволяет на основе шифраторов с внутренней гаммой создавать системы шифрованной связи практически любых размеров, не ограничивая их географию и количество абонентов. Современное развитие информационных технологий позволяет концентрировать значительное количество информации на физических носителях небольшого размера, что также обусловливает практическую применимость данного подхода. Задача построения системы шифрованной связи на основе шифраторов с внешней гаммой может иметь несколько подходов к ее решению. Например, исходя из установленного граничного значения объема ключевого документа, определяются оптимальное количество абонентов системы и допустимая нагрузка. С другой стороны, можно, исходя из требуемого количества абонентов и нагрузки на них, рассчитать необходимый объем ключевого документа. Шифрование методом гаммирования. Под гаммированием понимают процесс наложения по определенному закону гаммы шифра на открытые данные. Гамма шифра – это псевдослучайная последовательность, выработанная по заданному алгоритму для шифрования открытых данных и расшифрования принятых данных. Процесс шифрования заключается в генерации гаммы шифра и наложении полученной гаммы на исходный открытый текст обратимым образом, например, с использованием операции сложения по модулю 2. Перед шифрованием открытые данные разбивают на блоки одинаковой длины, обычно по 64 бита. Гамма шифра вырабатывается в виде последовательности аналогичной длины. Процесс расшифрования сводится к повторной генерации гаммы шифра и наложению этой гаммы на принятые данные. Получаемый этим методом шифротекст достаточно труден для раскрытия, поскольку теперь ключ является переменным. По сути дела, гамма шифра должна изменяться случайным образом для каждого шифруемого блока. Если период гаммы превышает длину всего шифруемого текста и злоумышленнику неизвестна никакая часть исходного текста, то такой шифр можно раскрыть только прямым перебором всех вариантов ключа. В этом случае криптостойкость шифра определяется длиной ключа. 6.2.2 Современные симметричные криптосистемы Американский стандарт шифрования данных DES. Стандарт шифрования данных DES (Data Encryption Standard) опубликован в 1977 г. Национальным бюро стандартов США. Он предназначен для защиты от несанкционированного доступа к важной, но не секретной информации в государственных и коммерческих организациях США. Основные достоинства алгоритма DES: используется только один ключ длиной 56 бит; относительная простота алгоритма обеспечивает высокую скорость обработки; достаточно высокая стойкость алгоритма. Алгоритм DES основан на комбинировании методов подстановки и перестановки и состоит из чередующейся последовательности блоков перестановки и подстановки. DES осуществляет шифрование 64-битовых блоков данных с помощью 64-битового ключа, в котором значащими являются 56 бит (остальные 8 бит – проверочные биты для контроля на четность). Расшифрование в DES является операцией, обратной шифрованию, и выполняется путем повторения операций шифрования в обратной последовательности. Обобщенная схема процесса шифрования в алгоритме DES показана на рисунке 6.5. 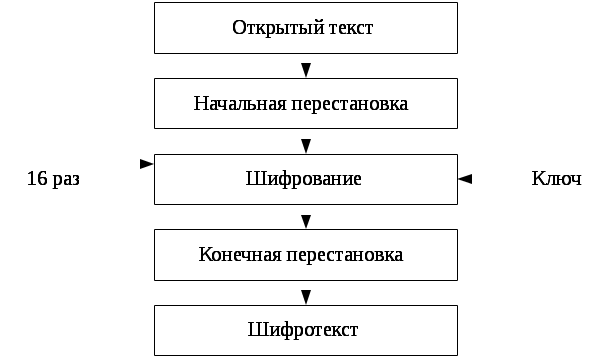 Рисунок 6.5 – Обобщенная схема шифрования в алгоритме DES Процесс шифрования заключается в начальной перестановке битов 64-битового блока, шестнадцати циклах шифрования и, наконец, в конечной перестановке битов. Стандарт шифрования данных (ГОСТ 28147-89). Алгоритм криптографического преобразования данных для систем обработки информации в сетях ЭВМ, отдельных вычислительных комплексах и ЭВМ был разработан в СССР и опубликован в виде государственного стандарта ГОСТ 28147-89 в 1989 году. Алгоритм криптографического преобразования данных предназначен для аппаратной и программной реализации, удовлетворяет криптографическим требованиям и не накладывает ограничений на степень секретности защищаемой информации. Алгоритм шифрования данных представляет собой 64-битовый блочный алгоритм с 256-битовым ключом. 6.3 Асимметричные криптосистемы Криптосистема шифрования данных RSA. Алгоритм RSA предложили в 1978 г. три автора: Р. Райвест (Rivest), А. Шамир (Shamir) и А. Адлеман (Adleman). Алгоритм получил свое название по первым буквам фамилий его авторов. Надежность алгоритма основывается на трудности факторизации больших чисел в произведение простых множителей. В криптосистеме RSA открытый ключ Кв, секретный ключ kв, сообщение М и криптограмма С принадлежат множеству целых чисел ZN = {0, 1, 2, ..., N – 1}, где N – модуль N = PQ. Здесь P и Q – случайные большие простые числа. Для обеспечения максимальной безопасности выбирают P и Q равной длины и хранят в секрете. Открытый ключ Кв выбирают случайным образом так, чтобы выполнялись условия: 1 < Кв (N), НОД(Кв, (N)) = 1, (N) = (P – 1) (Q – 1), где (N) – функция Эйлера. Второе из указанных выше условий означает, что открытый ключ Кв и значение функции Эйлера (N) должны быть взаимно простыми. Далее, используя расширенный алгоритм Евклида, вычисляют секретный ключ kв, такой, что kв = Кв–1 [mod(P – 1)(Q – 1)]. (6.1) Это можно осуществить, так как при известной паре простых чисел (P, Q) можно легко найти (N). Заметим, что kв и N должны быть взаимно простыми. Открытый ключ Кв используют для шифрования данных, а секретный ключ kв – для расшифрования. Преобразование шифрования определяет криптограмму С через пару «открытый ключ Кв, сообщение М» в соответствии со следующей формулой: C = Обратную задачу, т. е. задачу расшифрования криптограммы С, можно решить, используя пару «секретный ключ kв, криптограмма С» по следующей формуле: М = Таким образом, получатель, который создает криптосистему, защищает два параметра: секретный ключ kв и пару чисел (P, Q), произведение которых дает значение модуля N. С другой стороны, отправителю известны значения модуля N и открытого ключа Кв. Противнику известны лишь значения Кв и N. Если бы он смог разложить число N на множители P и Q, то он узнал бы тройку чисел {P, Q, Кв}, вычислил бы значение функции Эйлера (N) = (P –1)(Q – 1) и определил значение секретного ключа kв. Однако, разложение очень большого N на множители вычислительно не осуществимо (при условии, что длины выбранных P и Q составляют не менее 100 десятичных знаков). Схема шифрования Эль Гамаля. Схема Эль Гамаля, предложенная в 1985 г., может быть использована как для шифрования, так и для цифровых подписей. Безопасность схемы Эль Гамаля обусловлена сложностью вычисления дискретных логарифмов в конечном поле. Для того чтобы генерировать пару ключей (открытый ключ – секретный ключ), сначала выбирают некоторое большое простое число Р и большое целое число G, причем G < P. Числа Р и G могут быть распространены среди группы пользователей. Затем выбирают ключ X – случайное целое число, причем X < P. Число X является секретным ключом и должно храниться в секрете. Далее вычисляют Y = GX mod P. Число Y является открытым ключом. Для того чтобы зашифровать сообщение M, выбирают случайное целое число 1 < K< P – 1, такое, что числа К и (Р – 1) являются взаимно простыми. Затем вычисляют числа a = GK mod P, b = YK M mod P. Пара чисел (a, b) является шифротекстом. Длина шифротекста вдвое больше длины исходного открытого текста М. Для того чтобы расшифровать шифротекст (a, b), вычисляют M = b/aX mod P. (6.4) Комбинированный метод шифрования. Главным достоинством криптосистем с открытым ключом является их потенциально высокая безопасность: нет необходимости ни передавать, ни сообщать кому бы то ни было значения секретных ключей, ни убеждаться в их подлинности. В симметричных криптосистемах существует опасность раскрытия секретного ключа во время передачи. Однако алгоритмы, лежащие в основе криптосистем с открытым ключом, имеют следующие недостатки: генерация новых секретных и открытых ключей основана на генерации новых больших простых чисел, а проверка простоты чисел занимает много процессорного времени; процедуры шифрования и расшифрования, связанные с возведением в степень многозначного числа, достаточно громоздки. Именно поэтому быстродействие криптосистем с открытым ключом обычно в сотни и более раз меньше быстродействия симметричных криптосистем с секретным ключом. Комбинированный (гибридный) метод шифрования позволяет сочетать преимущества высокой секретности, присущие асимметричным криптосистемам с открытым ключом, с преимуществами высокой скорости работы, присущими симметричным криптосистемам с секретным ключом. При таком подходе криптосистема с открытым ключом применяется для шифрования, передачи и последующего расшифрования только секретного ключа симметричной криптосистемы. А симметричная криптосистема применяется для шифрования и передачи исходного открытого текста. В результате криптосистема с открытым ключом не заменяет симметричную криптосистему с секретным ключом, а лишь дополняет ее, позволяя повысить в целом защищенность передаваемой информации. Такой подход иногда называют схемой электронного цифрового конверта. Если пользователь А хочет передать зашифрованное комбинированным методом сообщение М пользователю В, то порядок его действий будет таков: 1 Создать (например, сгенерировать случайным образом) симметричный ключ, называемый в этом методе сеансовым ключом Кс. 2 Зашифровать сообщение М на сеансовом ключе Кс. 3 Зашифровать сеансовый ключ Кс на открытом ключе Кв пользователя В. 4 Передать по открытому каналу связи в адрес пользователя В зашифрованное сообщение вместе с зашифрованным сеансовым ключом. Действия пользователя В при получении зашифрованного сообщения и зашифрованного сеансового ключа должны быть обратными: 5 Расшифровать на своем секретном ключе kв сеансовый ключ Кс. 6 С помощью полученного сеансового ключа Кс расшифровать и прочитать сообщение М. При использовании комбинированного метода шифрования можно быть уверенным в том, что только пользователь В сможет правильно расшифровать ключ Кс и прочитать сообщение М. Комбинированный метод шифрования является наиболее рациональным, объединяя в себе высокое быстродействие симметричного шифрования и высокую криптостойкость, гарантируемую системами с открытым ключом. 6.4 Хэш-функции Хэш-функция предназначена для сжатия подписываемого документа M до нескольких десятков или сотен бит. Хэш-функция h(M) принимает в качестве аргумента сообщение (документ) M произвольной длины и возвращает хэш-значение h(M) = m фиксированной длины. Обычно хэшированная информация является сжатым двоичным представлением основного сообщения произвольной длины. Значение хэш-функции h(M) сложным образом зависит от документа M и не позволяет восстановить сам документ M. Функция h(M) – является хэш-функцией, если она удовлетворяет следующим условиям: исходный текст может быть произвольной длины; само значение h(M) имеет фиксированную длину; значение функции h(M) легко вычисляется для любого аргумента; восстановить аргумент по значению с вычислительной точки зрения – практически невозможно; функция h(M) – однозначна. Из определения следует, что для любой хэш-функции есть тексты-близнецы – имеющие одинаковое значение хэш-функции, так как мощность множества аргументов неограниченно больше мощности множества значений. Такой факт получил название «эффект дня рождения». Наиболее известные из хэш-функций – MD2, MD4, MD5 и SHA. Три алгоритма серии MD разработаны Ривестом в 1989-м, 90-м и 91-м годах соответственно. Все они преобразуют текст произвольной длины в 128-битную сигнатуру. Алгоритм MD2 предполагает: дополнение текста до длины, кратной 128 битам; вычисление 16-битной контрольной суммы (старшие разряды отбрасываются); добавление контрольной суммы к тексту; повторное вычисление контрольной суммы. Алгоритм MD4 предусматривает: дополнение текста до длины, равной 448 бит по модулю 512; добавление длины текста в 64-битном представлении; использование процедуры Damgard-Merkle с 512-битными блоками (в отличие от хэш-функции этот класс преобразований предполагает вычисление для аргументов фиксированной длины также фиксированных по длине значений), причем каждый блок участвует в трех разных циклах. В алгоритме MD4 довольно быстро были найдены «дыры», поэтому он был заменен алгоритмом MD5, в котором каждый блок участвует не в трех, а в четырех различных циклах. Алгоритм SHA (Secure Hash Algorithm) разработан NIST (National Institute of Standard and Technology) и повторяет идеи серии MD. В SHA используются тексты более 264 бит, которые закрываются сигнатурой длиной 160 бит. |
