Конспект лекций-СК. Конспект лекций В. В. Веселов СанктПетербург 2014 г. Лекция 1
 Скачать 1.5 Mb. Скачать 1.5 Mb.
|
Лекция 88. Расчет и конструирование изгибаемых элементов железобетонных конструкций. 8.1. Действительная работа и разрушение изгибаемых ж/б элементов.Изгибаемые элементы могут разрушаться как по нормальным, так и по наклонным сечениям (см. рис. 7.1). Разрушение по нормальным сечениям происходит в результате действия изгибающих моментов (в середине пролета – рис. 7.1), а по наклонным – в результате совместного действия моментов и поперечных сил или только поперечных сил, например, на приопорных участках балок (рис. 7.1). Задачей расчета является подбор наиболее рациональных размеров сечений изгибаемых элементов и определение требуемого количества продольной арматуры. Для составления расчетных зависимостей рассмотрим изменение напряженного состояния изгибаемых элементов в процессе увеличения нагрузки на них. Различают три стадии напряженного состояния изгибаемых элементов (рис. 8.1). Стадия I. При небольшой нагрузке деформации в бетоне носят упругий характер. Напряжения в бетоне невелики. Зависимость между напряжениями и деформациями почти линейная. Эпюры нормальных напряжений в сжатой и растянутой зонах сечений треугольные. При дальнейшем увеличении нагрузки в сжатой зоне эпюры напряжений продолжают оставаться треугольными, а в растянутой – становятся криволинейными в силу развития в бетоне пластических деформаций. Стадия I характеризует работу конструкции без поперечных трещин. Стадия II характеризует период появления и раскрытия трещин в растянутой зоне бетона. В сечениях, где возникали трещины, усилия растянутой зоны воспринимаются арматурой. Напряжения в бетоне растянутой зоны принимаются равными нулю. Напряжения в сжатой зоне вначале изменяются по линейному закону, а затем, с ростом нагрузки - по криволинейному, оставаясь при этом меньше временного сопротивления. Стадия Ш предшествует разрушению и характеризуется предельным состоянием прочности сечения. Напряжения в арматуре приближаются к физическому или условному пределу текучести, а напряжения в бетоне сжатой зоны - к временному сопротивлению. Разрушение может произойти либо в результате разрыва арматуры (случай I), либо в результате исчерпания прочности бетона (случай II). 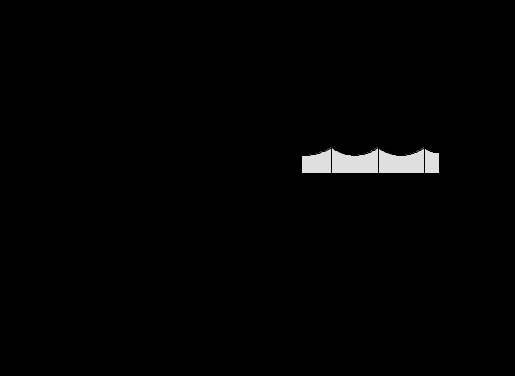 Рис. 8.1. Стадии напряженного состояния при изгибе. Рассмотренные напряженные состояния являются основой для составления расчетных зависимостей. При расчете по образованию трещин рассматривается стадия I, по раскрытию трещин - стадия II, по прочности - стадия III. Для упрощения расчетных формул криволинейные эпюры напряжений часто заменяются треугольными (в I и II стадиях) или прямоугольными (в стадии III). Это дает погрешность в пределах 5-10%, не более, но существенно упрощает расчетные зависимости. 8.2. Расчет прочности изгибаемых ж/б элементов по нормальным сечениям.Расчет прочности изгибаемых элементов прямоугольного сечения с одиночной арматурой. Элементы прямоугольного сечения являются наиболее распространенными и экономически выгодными. Расчетными формулами, полученными для прямоугольных сечений, часто пользуются и при расчете элементов таврового и двутаврового сечений. Расчетная схема элемента прямоугольного сечения при расчете по первой группе предельных состояний, т.е. по прочности, приведена на рис.8.2. 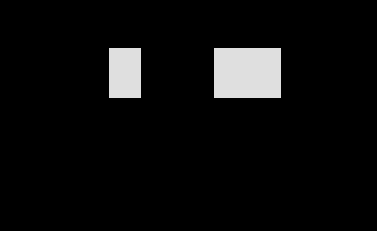 Рис. 8.2. Расчетная схема изгибаемого элемента прямоугольного сечения с одиночной арматурой. Равнодействующие усилий: в сжатой зоне  (8.1) (8.1)в растянутой зоне 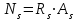 (8.2) (8.2)Момент внутренних сил относительно равнодействующей усилий в арматуре: 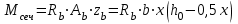 (8.3) (8.3)То же относительно равнодействующей усилий в сжатой зоне:  (8.4) (8.4)Для вычисления Мсеч необходимо найти х. Сделать это можно, составив уравнение суммы проекций всех сил на продольную ось элемента:  (8.5) (8.5)откуда 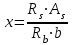 (8.6) (8.6)Пользуясь полученными зависимостями, можно вести проверку прочности и подбор сечений. Но на практике получил распространение метод подбора сечений с помощью таблиц. Если учесть, что  , т.е. момент, воспринимаемый сечением, равен или больше внешнего изгибающего момента, и ввести обозначение, , т.е. момент, воспринимаемый сечением, равен или больше внешнего изгибающего момента, и ввести обозначение, 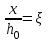 , то выражение 8.3 можно записать в виде: , то выражение 8.3 можно записать в виде: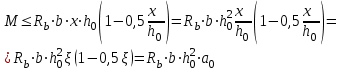 (8.7) (8.7)где 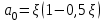 . .Аналогично выражение 8.4 может быть представлено в виде: 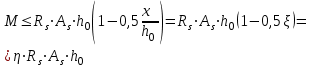 (8.8) (8.8)где 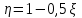 . .Величины α0, ξ и η взаимозависимы. Для них составлены таблицы. Поэтому достаточно найти одну из величин, а по ней можно определить и все другие. На практике вначале из выражения 8.7 вычисляют α0: 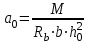 , (8.9) , (8.9)а далее по таблицам находят ξ и η. 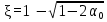 Такой подход реализуется, когда заранее задано значение h0. Можно задать значение ξ, по нему найти α0 и вычислить требуемое значение h0: 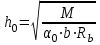 (8.10) (8.10)Наиболее экономичными получаются сечения, у которыхξ =0,3...0,4. Поэтому задаются этими значениями ξ и определяют остальные величины α0, η, h0, Аs. Величина Аs подбирается по сортаменту стержневой арматуры. Расчет прочности изгибаемых элементов прямоугольного сечения с двойной арматурой. Двойная арматура, т.е. устанавливаемая в растянутой и сжатой зонах, необходима тогда, когда разрушение идет по сжатой зоне. Положение границы между случаем I, когда разрушение идет по растянутой зоне и случаем 2, когда разрушение идет по сжатой зоне устанавливают в зависимости от относительной величины сжатой зоны ξR - граничного условия. Величина 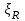 вычисляется по эмпирической формуле: вычисляется по эмпирической формуле: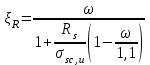 (8.11) (8.11)где ω - характеристика сжатой зоны бетона, определяемая по формуле: 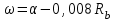 (8.12) (8.12)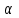 - коэффициент, принимаемый для тяжелого бетона равным 0,85, - коэффициент, принимаемый для тяжелого бетона равным 0,85,σsc,u- предельное напряжение в арматуре сжатой зоны. Если расчетом установлено, что относительная высота сжатой зоны ξ, вычисленная по формулам для элементов с одиночным армированием, оказалась больше ξR, то можно, не меняя размеров сечения элемента применить двойное армирование, т.е. усилить сжатую зону путем введения сжатой арматуры. Усиление сжатой зоны за счет постановки дополнительной арматуры ведет к увеличению расхода стали. Сечения с двойной арматурой менее экономичны. Применение двойной арматуры требует специального обоснования. Расчет сечения с двойной арматурой аналогичен расчету с одиночной арматурой, только к усилию в сжатой зоне бетона добавляется усилие в сжатой арматуре, равное RscּAś. Расчетная схема изгибаемого элемента с двойным армированием приведена на рис. 8.3.  Рис. 8.3. Расчетная схема изгибаемого элемента прямоугольного сечения с двойной арматурой. Основные условия равновесия для рассматриваемого случая имеют вид: 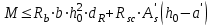 (8.13) (8.13)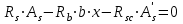 (8.14) (8.14)где а ́- расстояние от сжатой грани сечения до центра тяжести сжатой арматуры. Откуда находим: 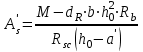 (8.15) (8.15)Если учесть, что 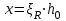 , то , то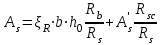 (8.16) (8.16)Рекомендуется величину внешнего момента, воспринимаемого сечением с двойной арматурой, ограничивать условием 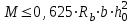 (8.17) (8.17)8.3. Расчет прочности изгибаемых ж/б элементов по наклонным сечениям.В наклонных сечениях наблюдаются те же три стадии напряженно-деформированного состояния, что и в нормальных сечениях, но характер разрушения несколько отличается от характера разрушения нормальных сечений. Разрушения могут быть двух типов (см. рис. 8.4). Первый тип разрушения происходит от достижения всей арматурой, пересекающей трещину, своих предельных значений (Rs и Rsw). При этом происходит значительное раскрытие трещин, сокращение высоты сжатой зоны и взаимный поворот двух частей относительно образовавшегося в сжатой зоне пластического шарнира. Второй тип разрушения происходит от разрушения бетона сжатой зоны (при срезе). При этом обе части смещаются относительно друг друга. Стараются проектировать изгибаемые элементы так, чтобы срез бетона не происходил, а ширина раскрытия наклонных трещин была ограниченной. Условия равновесия по изгибающему моменту и поперечной силе записываются в виде: 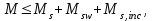 (8.18) (8.18)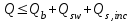 (8.19) (8.19)где M, Q - действующие на рассматриваемом участке изгибающий момент и поперечная сила; Ms, Msw, Ms,inc- моменты внутренних сил, создаваемых усилиями, соответственно, в продольной, поперечной и отогнутой арматуре относительно центра пластического шарнира; Qb, Qsw, Qs,inc - поперечные силы, воспринимаемые, соответственно, бетоном сжатой зоны, поперечной арматурой, отогнутыми стержнями.  а) б) Рис. 8.4. Схемы разрушения балок по наклонным сечениям: а) при достижении текучести арматуры, б) при сколе бетона в сжатой зоне.  Рис. 8.5. Схема усилий при расчете прочности изгибаемого элемента по наклонным сечениям. Приведенными выражениями можно пользоваться только при проверке прочности наклонных сечений, когда продольная и поперечная арматура уже подобраны. На практике при подборе поперечной арматуры и отгибов используются в основном эмпирические зависимости. Подбор поперечной арматуры, т.е. определения диаметра (dsw) и шага (s) производится в два этапа. Вначале по конструктивным соображениям устанавливают: - диаметр поперечной арматуры в зависимости от диаметра продольной арматуры (по условиям свариваемости) 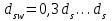 . .шаг поперечной арматуры по трем условиям: 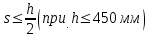 и и 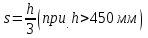 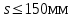 , ,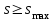 , т.е. максимально допустимого значения: , т.е. максимально допустимого значения: (8.20) (8.20)где Q - поперечная сила, Rbt - расчетное сопротивление бетона на растяжение при расчете по первой группе предельных состояний, b, h - размеры поперечного сечения, φb4- коэффициент, характеризующий вид бетона и принимаемый для тяжелого бетона равным 1,5. Из трех значений sназначается минимальное. Далее уточняется, достаточно ли ограничиться подбором поперечной арматуры по конструктивным требованиям или же необходимо еще уточнять dsw и s по расчету. Для этого проверяется условие:  (8.21) (8.21)где φb3 - коэффициент, характеризующий вид бетона и принимаемый для тяжелого бетона равным 0,6. Если условие выполняется, то на этом подбор поперечной арматурыи заканчивается. Но чаще всего это условие не выполняется. Тогда производят дополнительную проверку:  (8.22) (8.22)где Qb - поперечная сила, воспринимаемая бетоном сжатой зоны у конца наклонной трещины: 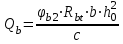 (8.23) (8.23)φb2- коэффициент, характеризующий вид бетона и принимаемый для тяжелого бетона равным 2; с - длина проекции наклонной трещины, принимаемая в пределах от с=h0 до с=3,33h0; Qsw - поперечная сила, воспринимаемая поперечной арматурой на длине проекции наиболее опасной наклонной трещины (c0): 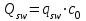 (8.24) (8.24) , (8.25) , (8.25)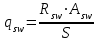 (8.26) (8.26)Rsw - расчетное сопротивление поперечной арматуры; Asw- площадь сечения поперечной арматуры  , (8.27) , (8.27)n- число каркасов в одном сечении изгибаемого элемента; asw - площадь сечения одного стержня поперечной арматуры. Если условие прочности наклонного сечения выполняется, то на этом расчет заканчивается, если нет - то либо уменьшается шаг стержней s, либо увеличивается диаметр поперечной арматуры (dsw), либо увеличивается прочность бетона, либо варьируются все параметры одновременно. Одновременно же при каждом значении суточняется величина поперечной силы Q, действующей в сечении на конце наклонной трещины. Для того, чтобы быстрее подобрать требуемую поперечную арматуру, рекомендуется начинать проверку, принимая с=3,33h0. Далее необходимо сделать проверку прочности по (сжатому) бетону между наклонными трещинами: 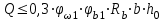 (8.28) (8.28)где 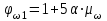 (8.29) (8.29)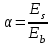 (8.30) (8.30)Es, Eb- модули упругости арматуры и бетона: 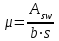 (8.31) (8.31)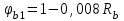 (8.32) (8.32)Rb- прочность бетона на сжатие в МПа. Указанное условие обычно выполняется, если выполнено условие прочности по наклонной трещине. Лекция 9 9. Расчет и конструирование сжатых и растянутых элементов железобетонных конструкций. |
