АИИК-испр 29-12-2015 (1). Конспект лекций введение. Понятие об автоматических системах
 Скачать 1.74 Mb. Скачать 1.74 Mb.
|
|
Параметрически оптимизируемый алгоритм управления второго порядка и его модификация Алгоритм управления второго порядка ПИД-регулятора имеет следующую структуру: 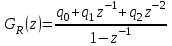 . (3.17) . (3.17)Разностное уравнение, описывающее регулятор с передаточной функцией (3.17), будет иметь вид: 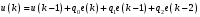 . (3.18) . (3.18)Рассматривая единичное ступенчатое изменение сигнала ошибки 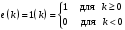 , (3.19) , (3.19)сформируем систему уравнений для последовательных значений выходного сигнала регулятора u(k), следующих из (3.18): 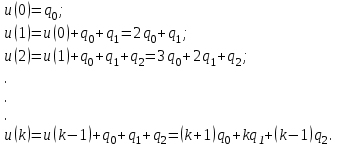 (3.20) (3.20)В случае, когда u(1)<u(0), дискретный регулятор соответствует непрерывному ПИД-регулятору с дополнительной задержкой сигнала на один такт. Если параметр регулятора q0>0, то можно записать следующие соотношения для параметров q0, q1 и q2: при u(1)<u(0): q0+q1<0 или q1<-q0 (3.21) при u(k)>u(k-1) для k³2: q0+q1+q2>0 или q2>-(q0+q1). Таким образом, обобщая допустимые диапазоны изменения параметров регулятора, получим q0>0; q1<-q0; -(q0+q1)<q2<q0 (3.22) Реакция регулятора на единичное ступенчатое воздействия приведена на рис. 3.5. 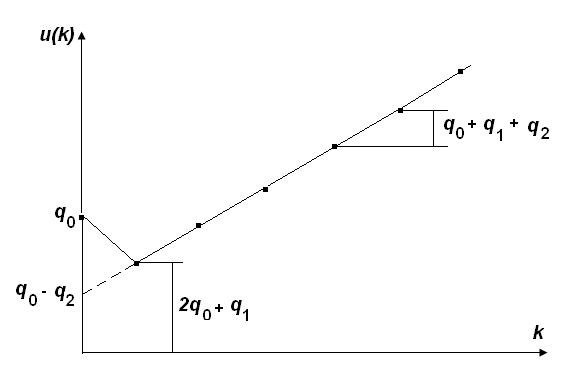 Рис. 3.5. Переходный процесс для алгоритма управления второго порядка Определим следующие коэффициенты, характеризующие свойства регулятора: 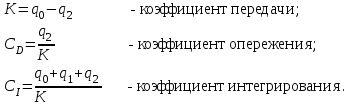 (3.23) (3.23)Коэффициенты (3.23) при малых значениях такта квантования связаны с соответствующими коэффициентами непрерывных ПИД-алгоритмов управления следующими соотношениями: 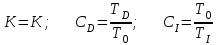 . (3.24) . (3.24)Из соотношений (3.24) видно, что для малых тактов квантования коэффициенты передачи регуляторов тождественно равны. Коэффициент опережения CD равен отношению постоянной дифференцирования к такту квантования, а коэффициент интегрирования CI – отношению такта квантования к постоянной интегрирования. Учитывая условия (3.22), получим, что 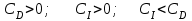 (3.25) (3.25)Если рассмотренные выше коэффициенты подставить в выражение (3.17), то дискретная передаточная функция регулятора примет вид 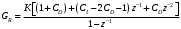 . (3.26) . (3.26)Необходимо отметить, что рассмотренный выше алгоритм управления второго порядка является аналогом непрерывного ПИД-регулятора с положительными параметрами только в том случае, если выполняются условия (3.22) или (3.25). В общем случае параметры регулятора, определенные в результате оптимизации, могут и не удовлетворять этим условиям, что зависит от характеристик конкретного объекта управления, вида критерия оптимизации и возмущающего сигнала. Для уменьшения больших изменений управляющей переменной при резких изменениях задающего сигнала задающее воздействие w(k) исключают из дифференцирующего члена. В результате этого вместо обычного алгоритма ПИД-регулятора 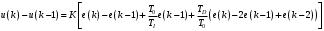 (3.27) (3.27)используется модифицированный алгоритм 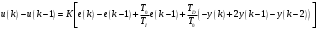 , (3.28) , (3.28)где e(k)=w(k)-y(k). Дополнительного уменьшения амплитуды управляющей переменной добиваются, оставляя значения задающего сигнала только в интегрирующем члене алгоритма: 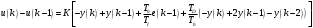 . (3.29) . (3.29)Приведенные модифицированные алгоритмы менее чувствительны к высокочастотным составляющим сигнала w(k) по сравнению с сигналом y(k). Поэтому параметры регуляторов, полученные в результате оптимизации для определенных типов возмущений, например, для возмущений на входе объекта и на выходе системы, будут отличаться незначительно. Существенные изменения управляющей переменной могут быть также уменьшены путем ограничения скорости изменения задающей и (или) управляющей переменной. Поскольку такие ограничения оказываются эффективными для всех типов возмущений, их применение предпочтительнее использования модифицированных алгоритмов управления, описываемых уравнениями (3.28) и (3.29). |
