АИИК-испр 29-12-2015 (1). Конспект лекций введение. Понятие об автоматических системах
 Скачать 1.74 Mb. Скачать 1.74 Mb.
|
|
АВТОМАТИЗАЦИЯ ПРОЦЕССОВ ИЗМЕРЕНИЙ, ИСПЫТАНИЙ И КОНТРОЛЯ (Конспект лекций) ВВЕДЕНИЕ. ПОНЯТИЕ ОБ АВТОМАТИЧЕСКИХ СИСТЕМАХ Управление каким-либо объектом — это процесс воздействия на него с целью обеспечения требуемого течения процессов в нем или требуемого изменения его состояния. Основой управления является обработка информации о состоянии объекта в соответствии с целью управления. Управление, осуществляемое без участия человека, называется автоматическим управлением. Техническое устройство, с помощью которого осуществляется автоматическое управление объектом, называется управляющим устройством. Совокупность объекта управления и управляющего устройства образует систему автоматического управления (САУ). В общем виде система автоматического управления представлена на рис. В-1, а, где О — объект управления, УУ — управляющее устройство. Состояние объекта характеризуется выходной величиной X. В общем случае выходных величин несколько, и тогда состояние объекта характеризуется вектором X, координатами которого являются отдельные выходные величины. От управляющего устройства на вход объекта поступает управляющее воздействие U. Помимо управляющего воздействия, к объекту приложено также возмущающее воздействие (возмущение, помеха) F, которое изменяет состояние объекта, т. е. X, препятствуя управлению. На вход управляющего устройства подается задающее воздействие Х3, содержащее информацию о требуемом значении X, т. е. о цели управления. Переменные U, Х3 и F в общем случае являются векторами, как и X. Как показано на рис. В-1, а, в самом общем случае на вход управляющего устройства, помимо задающего воздействия Х3, поступает также информация о текущем состоянии объекта в виде выходной величины X и о действующем на объект возмущении F. Управляющее устройство перерабатывает получаемую информацию по определенному заложенному в нем алгоритму (закону). В результате на его выходе возникает управляющее воздействие. 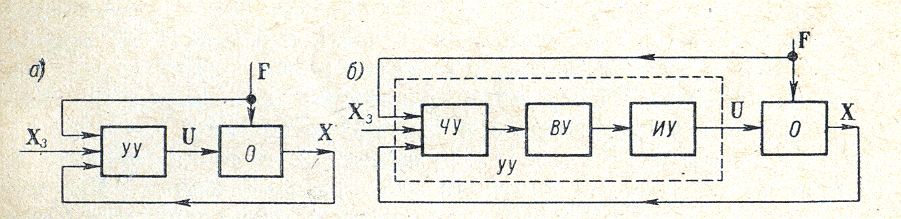 Рис. В-1. Блок-схема (а) и функциональная схема (б) системы автоматического управления На рис. В-1, б изображена функциональная схема САУ, на которой показаны основные составные части управляющего устройства: чувствительное устройство ЧУ, вычислительное устройство ВУ и исполнительное устройство ИУ. Чувствительные ус т р о и с т в а (измерительные устройства, датчики) служат для измерения подаваемых на управляющее устройство воздействий (сигналов) X, Х3 и F. Вычислительное устройство реализует алгоритм работы управляющего устройства. В простейшем случае оно осуществляет простые математические операции, такие как операция сравнения, определяющая разность Х3 — X, операции интегрирования, дифференцирования, статического нелинейного преобразования и т. п. В более сложных случаях вычислительное устройство может представлять собой компьютер. Исполнительные устройства предназначены для непосредственного управления объектом, т. е. изменения его состояния в соответствии с сигналом, выдаваемым вычислительным устройством. Помимо перечисленных выше частей, в состав управляющего устройства могут входить различные специальные устройства, например преобразователи, служащие для согласования отдельных частей системы, устройства связи и т. п. КЛАССИФИКАЦИЯ АВТОМАТИЧЕСКИХ СИСТЕМ Для ознакомления с основными видами систем автоматического управления и соответствующей терминологией рассмотрим классификацию САУ по ряду признаков, существенных с точки зрения теории автоматического управления. А. Разомкнутые, замкнутые и комбинированные системы В схеме САУ, изображенной на рис. В-1, на управляющее устройство поступают три вида информации: информация о величине X, определяющей состояние объекта, информация о величине Хз, задающей цель управления, информация о F — возмущениях, нарушающих режим работы объекта. Однако возможны САУ, в которых используется лишь часть перечисленной информации. При этом в зависимости от видов используемой управляющим устройством информации различают два основных типа САУ — разомкнутые системы и замкнутые системы. В разомкнутых САУ выходная величина объекта X не измеряется, т. е. нет контроля за состоянием объекта. Разомкнутыми такие системы называются потому, что вследствие этого в них отсутствует обратная связь между выходом объекта и входом управляющего устройства, при наличии которой объект и управляющее устройство образуют замкнутый контур. Возможны разомкнутые САУ, в которых управляющее устройство измеряет только одно задающее воздействие Х3, одно возмущение F и, наконец, оба эти сигнала одновременно. В первом варианте разомкнутой САУ управление осуществляется по задающему воздействию: поступающие извне команды Х3 приводят путем изменения управляющего воздействия U к соответствующему изменению выходной величины объекта X. Точность обеспечиваемого при этом соответствия между X и Х3 целиком определяется постоянством параметров системы и возмущений и никак не контролируется. Поэтому практически такие системы пригодны лишь при достаточно высокой стабильности указанных выше условий работы системы и невысоких требованиях к точности. Вторым вариантом разомкнутой САУ является система автоматического управления по возмущению, или, как ее еще называют, система автоматической компенсации. Такие системы нашли применение, в частности, когда задачи управления сводятся к поддержанию постоянства выходной величины X объекта. Система управления по задающему и возмущающему воздействиям является наиболее полным видом разомкнутой САУ. В этом случае управление объектом осуществляется в функции двух величин Х3 и F, т. е. здесь объединены оба предыдущих варианта разомкнутых систем. Принцип компенсации возмущения позволяет существенно повысить точность управления в разомкнутых САУ. Однако все же эта точность остается невысокой, во-первых, вследствие невозможности охватить компенсацией все возмущения, действующие на систему (в том числе и на управляющее устройство), и, во-вторых, из-за изменения во времени параметров объекта и управляющего устройства. Последнее в полной мере относится и к параметрам цепи компенсации. Неточность и изменение настройки цепи компенсации тоже вызывают изменение выходной величины объекта. В силу изложенного разомкнутые САУ нашли применение только при невысоких требованиях к точности управления. В замкнутых САУ на вход управляющего устройства подаются задающее воздействие Х3 и выходная величина объекта X. Исходя из величины Х3, управляющее устройство определяет соответствующее требуемое значение X и, имея информацию о текущем значении X, обеспечивает необходимое соответствие между X и Х3 путем воздействия на объект. В такой САУ управляющее устройство стремится ликвидировать все отклонения X от его значения, определяемого заданием Х3, независимо от причин, вызвавших эти отклонения, включая любые возмущения, внешние и внутренние помехи, а также изменения параметров системы. Как видно из рис. В-1, САУ такого типа представляют собой замкнутый контур, образованный объектом и управляющим устройством. При этом управляющее устройство создает обратную связь вокруг объекта, связывая его выход с входом. Замкнутые САУ называются, поэтому еще системами с обратной связью или системами управления по отклонению. Эти системы могут обеспечить принципиально неограниченную точность управления и представляют собой основной тип САУ. Комбинированные САУ представляют собой объединение в одну систему замкнутой системы управления по отклонению и разомкнутой системы управления по внешнему воздействию. Показанная на рис. В-1 схема является схемой такой комбинированной САУ. Добавление к замкнутой системе управления разомкнутой системы компенсации влияния на выходную величину объекта какого-либо возмущения облегчает задачу замкнутой САУ и тем самым позволяет упростить ее и повысить точность управления. Лучшее качество управления в комбинированных системах объясняется тем, что в них наиболее полно используется информация об объекте и внешней ситуации. Б. Автоматические системы — системы стабилизации, системы программного управления и следящие системы Частным, но широко распространенным видом систем автоматического управления являются системы автоматического регулирования (САР). Системой автоматического регулирования называется САУ, задача которой заключается в поддержании выходной величины объекта X на заданном уровне Х3, т. е. поддержание равенства X = Х3. В зависимости от характера задающего воздействия САР делятся на три вида: системы стабилизации, системы программного управления и следящие системы. В системах стабилизации задающее воздействие постоянно, в системах программного управления оно изменяется по заранее заданному закону, в следящих системах оно тоже изменяется, но закон изменения заранее не известен. В последнем случае задающее воздействие поступает в систему извне и задачей системы является обеспечение слежения выходной величиной объекта за изменяющейся задающей величиной так, чтобы все время поддерживалось равенство X= Х3. Управляющее устройство в системах автоматического регулирования называется регулятором, а выходная величина — регулируемой величиной. В. Одномерные и многомерные системы В зависимости от количества выходных координат объекта управления, образующих вектор выходной величины X, САУ делятся на: одномерные и многомерные (двухмерные и т. д.). Многомерные САУ (и САР), в свою очередь, делятся на системы связанного и несвязанного управления (регулирования). Система несвязанного управления имеет несколько управляющих устройств, каждое из которых осуществляет управление своей выходной координатой объекта. При этом все эти устройства не имеют взаимных связей. (Последнее, однако, не исключает возможности влияния управляющих устройств друг на друга через объект управления или, например, общий источник питания.) В системе связанного управления отдельные управляющие устройства связаны друг с другом внешними связями. Входящая в состав многомерной системы управления (как связанной, так и несвязанной) отдельная система управления называется автономной, если управляемая ею выходная координата объекта не зависит от значений остальных его координат, так что изменение последних не вызывает изменения этой координаты. Г. Системы линейные и нелинейные Линейной называется система, которая описывается линейными дифференциальными уравнениями. В противном случае система является нелинейной. Чтобы система была нелинейной, достаточно иметь в ее составе хотя бы одно нелинейное звено, т. е. звено, описываемое нелинейным уравнением. Для линейных систем справедлив принцип суперпозиции. Он заключается в том, что реакция системы на любую комбинацию внешних воздействий равна сумме реакций на каждое из этих воздействий, поданных на систему отдельно. Принцип суперпозиции позволяет выразить реакцию системы на любое произвольное воздействие через реакцию системы на элементарное типовое воздействие, например, в виде ступеньки. Для этого достаточно представить данное входное воздействие в виде совокупности выбранных типовых воздействий. Благодаря принципу суперпозиции разработана общая теория линейных систем автоматического управления, описываемых линейными дифференциальными уравнениями любого порядка. К нелинейным системам принцип суперпозиции не применим. Нет и общей теории нелинейных дифференциальных уравнений, на основе которой могла бы быть создана общая теория нелинейных систем автоматического управления. Существует лишь ряд частных методов для решения некоторых видов нелинейных уравнений невысокого порядка. Вместе с тем, если не ограничивать диапазона изменения входных воздействий, то все реальные системы автоматического управления оказываются нелинейными. Трудность исследования нелинейных систем заставляет упрощать их описание. Желательным пределом такого упрощения является приближенное описание их линейными уравнениями, хотя бы в некоторых из интересующих нас режимов. Это называется линеаризацией нелинейных систем. В тех случаях, когда линеаризация невозможна, прибегают к приближенным методам исследования нелинейных систем с учетом их нелинейностей. Д. Системы стационарные и нестационарные Стационарной называется система, все параметры которой не изменяются во времени. Нестационарная система — это система с переменными параметрами. При математическом описании нестационарной системы это проявляется в том, что некоторые коэффициенты дифференциального уравнения системы являются функциями времени. В соответствии с данным определением, в отличие от нестационарной системы, реакция стационарной системы на одно и то же воздействие не зависит от момента приложения этого воздействия. |
