АИИК-испр 29-12-2015 (1). Конспект лекций введение. Понятие об автоматических системах
 Скачать 1.74 Mb. Скачать 1.74 Mb.
|
|
НЕОБХОДИМОЕ И ДОСТАТОЧНОЕ УСЛОВИЕ ПОЛНОЙ НАБЛЮДАЕМОСТИ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ СИСТЕМЫ. ОБНАРУЖИВАЕМОСТЬ На предыдущих лекциях при стабилизации системы с уравнением состояния 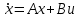 (6.1) (6.1)обратной связью и = Кх мы предполагали доступность измерению в любой момент времени всех компонент вектора состояния х. В общем случае поддается измерению (наблюдению) вектор у,связанный с вектором состояния х уравнением 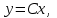 (6.2) (6.2)которое называют уравнением выхода, или уравнением наблюдения. В связи с этим возникает проблема наблюдаемости, заключающаяся в установлении возможности определения состояния по измеренным значениям входа и выхода на некотором интервале. Система (6.1), (6.2) называется полностью наблюдаемой, если по данным измерения входного 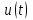 и выходного и выходного 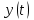 сигналов на промежутке сигналов на промежутке 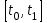 можно определить состояние x=x(t0). можно определить состояние x=x(t0).Построим матрицу из строк матриц 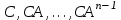 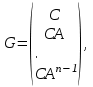 (6.3) (6.3)которую назовем матрицей наблюдаемости. Система (6.1), (6.2) полностью наблюдаема тогда и только тогда, когда ранг матрицы наблюдаемости равен порядку системы: rank  (6.4) (6.4)Пример. Является ли вполне наблюдаемой система с уравнениями движения 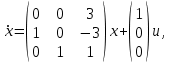 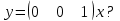 Решение. Вычислим строки матрицы наблюдаемости: 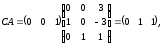 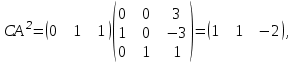 Таким образом, 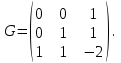 Так как rank G=3, то система вполне наблюдаема. Предположим, что ранг матрицы наблюдаемости (6.3) равен l. Тогда у этой матрицы есть l линейно независимых строк. Обозначим через 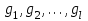 линейно независимые строки матрицы G. Пусть матрица H в качестве первых l строк имеет строки линейно независимые строки матрицы G. Пусть матрица H в качестве первых l строк имеет строки 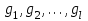 : :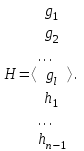 (6.5) (6.5)Остальные 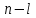 строк этой матрицы строк этой матрицы 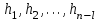 выбираются произвольно, но так, чтобы det выбираются произвольно, но так, чтобы det 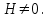 При замене вектора состояния х по формуле 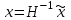 для нового вектора состояния для нового вектора состояния 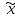 получаем уравнения получаем уравнения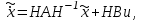 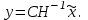 (6.6) (6.6)Матрицы  и и 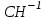 имеют следующую структуру: имеют следующую структуру: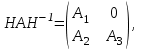 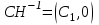 (6.7) (6.7)где 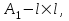 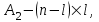 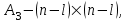 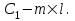 Обозначим вектор-столбец, образованный первыми lкомпонентами вектора состояния 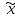 , через , через 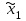 , а вектор-столбец, образованный последующими , а вектор-столбец, образованный последующими 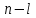 компонентами, через компонентами, через 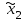 . Тогда уравнения движения (6.6) можно записать следующим образом: . Тогда уравнения движения (6.6) можно записать следующим образом: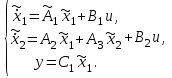 (6.8) (6.8)Ранг матрицы 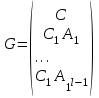 (6.9) (6.9)равен l. Поэтому подсистема  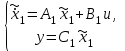 (6.10) (6.10)вполне наблюдаема. Подсистема  (6.11) (6.11)не оказывает никакого влияния на выходной сигнал, это ненаблюдаемая подсистема исходной системы. Уравнения (6.8) называют канонической формой наблюдаемости для исходных уравнений состояния (6.1) и выхода (6.2). Переход от системы (6.1), (6.2) к канонической форме наблюдаемости (6.8) осуществляется заменой переменной 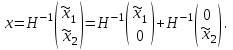 (6.12) (6.12)Равенство (6.12) позволяет представить вектор состояния х в виде суммы наблюдаемой 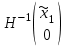 и ненаблюдаемой и ненаблюдаемой 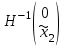 составляющих. составляющих.Система (6.1), (6.2) называется обнаруживаемой, если ненаблюдаемые координаты при нулевых остальных координатах и нулевом входном воздействии стремятся к нулю. Необходимым и достаточным условием обнаруживаемости линейной стационарной системы является отрицательность вещественных частей всех собственных чисел матрицы A3 в канонической форме наблюдаемости. Пример. Найти каноническую форму наблюдаемости для системы с уравнениями движения 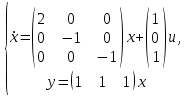 Решение. Вычислим строки матрицы наблюдаемости 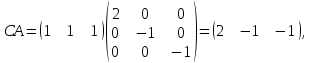  Матрица наблюдаемости 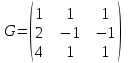 имеет ранг 2. Ее первые две строки линейно независимы. Строим матрицу (6.5): 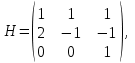 выбрав третью строку произвольно, но так, чтобы det 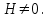 Выполним замену 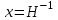 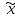 : :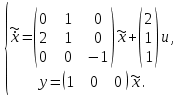 Координаты 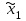 , , 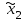 наблюдаемы, координата наблюдаемы, координата 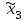 не наблюдаема. не наблюдаема. АСИМПТОТИЧЕСКАЯ ОЦЕНКА СОСТОЯНИЯ. НАБЛЮДАТЕЛИ ПОЛНОГО ПОРЯДКА Рассмотрим линейную стационарную систему с уравнениями движения 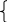 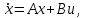 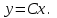 (7.1) (7.1)По результатам наблюдения входного 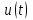 и выходного сигналов системы (7.1) на промежутке и выходного сигналов системы (7.1) на промежутке 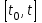 требуется восстановить текущее значение состояния системы. Восстановленное значение требуется восстановить текущее значение состояния системы. Восстановленное значение  фазового вектора фазового вектора 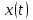 называется его асимптотической оценкой при условии, что ошибка восстановления называется его асимптотической оценкой при условии, что ошибка восстановления 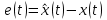 с течением времени стремится к нулю. с течением времени стремится к нулю.Наблюдателем, или системой, асимптотической оценки называется устройство, формирующее асимптотическую оценку  фазового вектора системы (7.1) по измерениям управления фазового вектора системы (7.1) по измерениям управления 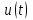 и выходного сигнала и выходного сигнала 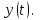 Наблюдатель с коррекцией описывается уравнением по ошибке восстановления 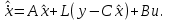 (7.2) (7.2)Матрица 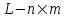 называется матрицей коэффициентов усиления наблюдателя. Наблюдатель (7.2) называют наблюдателем полного порядка, так как размерность пространства состояния наблюдателя и пространства состояния системы (7.1) совпадают. называется матрицей коэффициентов усиления наблюдателя. Наблюдатель (7.2) называют наблюдателем полного порядка, так как размерность пространства состояния наблюдателя и пространства состояния системы (7.1) совпадают.Необходимым и достаточным условием возможности построения наблюдателя для системы (7.1) является обнаруживаемость этой системы. При этом скорость затухания ошибки наблюдения уже не может быть произвольной, так как затухание ошибки оценивания ненаблюдаемой составляющей определяется только исходной системой. Пример. Построить наблюдатель полного порядка для линейной стационарной системы  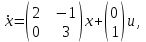 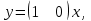 обеспечив выбором коэффициентов усиления наблюдателя собственные числа 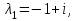 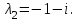 Решение. Обозначим элементы матрицы Lчерез l1 и l2. Тогда 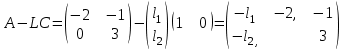 . .Найдем характеристический полином матрицы 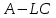 : :det 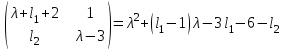 . .Полином с корнями 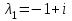 и и 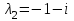 имеет вид имеет вид 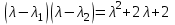 . Сравнение коэффициентов этого полинома и характеристического полинома матрицы . Сравнение коэффициентов этого полинома и характеристического полинома матрицы 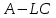 дает систему двух уравнений дает систему двух уравнений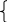 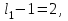 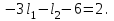 для определения 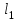 и и 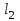 . В результате получим . В результате получим 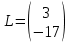 . .Математическая модель ПИД-регулятора Обоснование выбора цифрового регулятора При разработке электронных, пневматических или гидравлических аналоговых регуляторов по техническим соображениям вынуждены пользоваться достаточно узким набором элементов, действующих как интеграторы (И), дифференциаторы (Д) и пропорциональные усилители (П). В силу этого при синтезе систем управления аналогового типа приходится сталкиваться с весьма серьезными ограничениями. Гибкость программных средств существенно расширяет возможность реализации сложных алгоритмов для управляющих компьютеров. Это создает предпосылки для практического применения новейших методов современной теории управления. Для создания эффективного управляющего алгоритма конкретной прикладной задачи необходимо иметь достаточно полное описание объекта в форме его математической модели, а также должны быть известны показатели, по которым можно сравнивать алгоритмы различных типов. Такими показателями служат качество управления, обеспечиваемое алгоритмом, сложность его реализации, чувствительность к изменению параметров и воздействию помех, требуемая производительность ЭВМ, а также некоторые свойства объекта управления (его линейность или нелинейность, расположение полюсов и нулей, наличие задержек, структура связей в многосвязном объекте). Выделяют две основные группы систем управления: параметрически и структурно оптимизируемые. Системы, структура которых, т.е. вид и порядок описывающих их уравнений, заданы, а свободные параметры подстраиваются под управляемый объект с использованием критерия оптимизации или определенных правил настройки, являются параметрически оптимизируемыми. Системы управления являются структурно оптимизируемыми, если и структура, и параметры регулятора оптимально подстраиваются под структуру и параметры модели объекта. В каждой из двух основных групп регуляторов можно выделить несколько подгрупп: для параметрически оптимизируемых регуляторов это различные типы ПИД-регуляторов. Структурно оптимизируемые регуляторы подразделяются на компенсационные регуляторы и регуляторы с управлением по состоянию (регуляторы состояния). В данной работе используется параметрически оптимизируемый регулятор. Поскольку, как правило, к параметрически оптимизируемым относят широко используемые П-, ПИ- и ПИД-регуляторы, то для решения поставленной задачи преобразуем их уравнение с помощью дискретизации. Такой подход позволяет использовать накопленный опыт работы с аналоговыми регуляторами и применять известные правила настройки параметров. Более того, в этом случае нет необходимости проводить переподготовку обслуживающего персонала. Дискретное представление дифференциальных уравнений непрерывных ПИД-регуляторов При исследовании систем управления с компьютерами широкое использование получило z-преобразование. Возможность применения этого математического аппарата определяется тем, что все величины, характеризующие состояние объекта, рассматриваются в дискретные моменты времени t=kT0, где k=0, 1, 2…, Т0 – период такта квантования. Идеализированное уравнение ПИД-регулятора имеет вид: 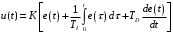 , (3.7) , (3.7)где К – коэффициент передачи, TI – постоянная интегрирования, TD – постоянная дифференцирования. Для малых тактов квантования Т0 это уравнение можно преобразовать в разностное с помощью дискретизации, состоящей в замене производной разностью первого порядка, а интеграла – суммой. Непрерывное интегрирование может быть заменено интегрированием по методу прямоугольников или трапеций. При использовании метода прямоугольников получаем 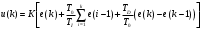 . (3.8) . (3.8)На основании выполненных расчетов получен нерекуррентный алгоритм управления. В нем для формирования суммы необходимо учитывать все предыдущие значения сигнала ошибки e(t). Поскольку каждый раз значение управляющего сигнала u(k) вычисляется заново, этот алгоритм является "позиционным". Однако для программирования на компьютере более удобны рекуррентные алгоритмы. Они отличаются тем, что для вычисления текущего значения управляющей переменной u(k) используется ее предыдущее значение u(k-1) и поправочный член. Для получения рекуррентного алгоритма достаточно вычесть из уравнения (3.8) следующее уравнение: 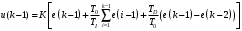 . (3.9) . (3.9)В результате получим 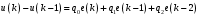 , (3.10) , (3.10)где 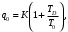 (3.11) (3.11)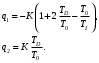 Этот алгоритм является «скоростным», так как теперь вычисляется только текущее приращение управляющей переменной: 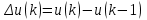 . (3.12) . (3.12)Рассмотрим простой контур управления, изображенный на рис. 3.4. Дискретная передаточная функция объекта управления с экстраполятором нулевого порядка имеет вид: 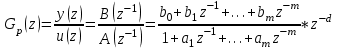 . (3.13) . (3.13)Обобщенная дискретная передаточная функция линейного регулятора записывается как  . (3.14) . (3.14)Этот алгоритм может быть реализован, если р0¹0. Однако соотношение порядков числителя и знаменателя передаточной функции могут быть различными: n£m или n>m. Обычно в таких регуляторах q0¹0, а значение р0 выбирается равным 1.  Рис. 3.4. Одноконтурная система управления В структурно оптимизируемых регуляторах порядки числителя и знаменателя передаточной функции m и n являются функциями соответствующих порядков модели объекта. Например, для апериодических регуляторов n=m и m=m+d. Однако в параметрически оптимизируемых регуляторах порядок регулятора может быть меньше порядка модели объекта, n£m и m£m+d. Следовательно, параметрически оптимизируемые регуляторы требуют меньших затрат машинного времени. При выборе структуры параметрически оптимизируемых регуляторов, как правило, необходимо гарантировать, чтобы изменения задающей переменной w(k) и возмущений (рис. 3.4.) не приводили к появлению статической ошибки по сигналу e(k). На основании теоремы z-преобразования о конечном значении для выполнения этого условия необходимо, чтобы передаточная функция регулятора имела полюс z=1. Следовательно, простейшие алгоритмы управления n-го порядка будут иметь следующую структуру: 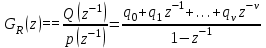 (3.15) (3.15)При n=1 и соответствующем выборе параметров получаем регулятор типа ПИ, при n=2 – ПИД, при n=3 – типа ПИД2 и т.д. Разностное уравнение, описывающее регулятор с передаточной функцией (3.15), имеет вид: 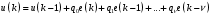 . (3.16) . (3.16)Для получения требуемого качества процессов управления параметры q0, q1, q2, … qn должны выбираться с учетом характеристик объекта. Расчет этих параметров может быть выполнен следующим образом: на основе метода, использующего модель объекта управления, в результате минимизации критерия качества с использованием параметрической оптимизации, причем аналитическое решение возможно лишь для объектов и регуляторов очень низкого порядка; в остальных случаях следует применять численные методы; с использованием алгоритмов параметрической настройки, позволяющих получить параметры регулятора, близкие к оптимальным для некоторого критерия. На практике обычно оценивают либо параметры переходного процесса в системе при ступенчатом задающем воздействии, либо критическое значение коэффициента усиления и период колебаний на границе устойчивости системы; путем последовательного увеличения значений параметров от малых начальных значений до тех пор, пока процесс в замкнутой системе не приобретет значительной колебательности, с дальнейшим уменьшением значения параметров (метод проб и ошибок). |
