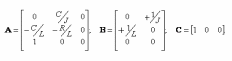АИИК-испр 29-12-2015 (1). Конспект лекций введение. Понятие об автоматических системах
 Скачать 1.74 Mb. Скачать 1.74 Mb.
|
|
А - функциональная матрица размером n x n, называемая матрицей состояния системы (объекта); В - функциональная матрица размером n x r, называемая матрицей управления (входа); С - функциональная матрица размером m x n, называемая матрицей выхода по состоянию; D - функциональная матрица размером m x r, называемая матрицей выхода по управлению. Матрица D отлична от нуля в случаях, когда в передаточной функции рассматриваемой системы порядок числителя равен порядку знаменателя. Поскольку в реальных системах порядок числителя, как правило, всегда меньше порядка знаменателя, матрица D считается равной нулю. Пример. На рис. 2. показан электродвигатель постоянного тока независимого возбуждения, работающий при постоянном магнитном потоке (Ф=const). 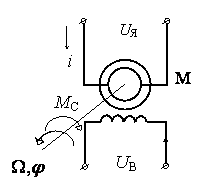 Рис.2.Электродвигатель постоянного тока Дифференциальные уравнения для такого объекта могут быть записаны относительно следующих переменных состояния: - скорости вращения ротора, тока якоря i(t), углового перемещения ротора . При использовании знакомых зависимостей для электродвижущей силы и вращающего момента двигателя получим уравнение электрической цепии уравнения вращающейся части: C*i=J 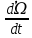 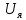 (t)= (t)=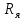 i(t) + i(t) + 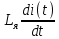 + CΩ + CΩ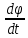 =Ω =Ωгде J – приведенный момент инерции электродвигателя. Выразим все уравнения относительно производных: 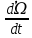 =С/J*i =С/J*i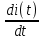 = =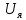 (t)/ (t)/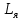 - - 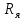 / /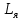 *i(t) – C/ *i(t) – C/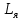 *Ω *Ω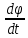 =Ω =Ω
Таким образом для рассматриваемой системы матрицы А, В, С векторно-матричной модели будут иметь следующий вид:
Представляя векторы состояния, входа и выхода как 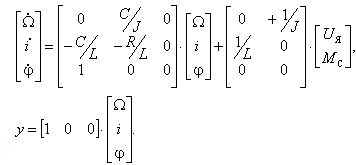 ДОСТАТОЧНОЕ УСЛОВИЕ СТАБИЛИЗЙРУЕМОСТИ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ НЕПРЕРЫВНОЙ СИСТЕМЫ Необходимым и достаточным условием асимптотической устойчивости линейной стационарной системы с уравнением состояния 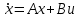 (1.1) (1.1)является отрицательность вещественных частей всех собственных чисел матрицы А. Если в любой момент времени доступен для измерения вектор состояния, то на вход системы (1.1) может быть подан сигнал 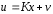 , (1.2) , (1.2)где 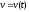 — некоторое внешнее воздействие. В результате подстановки (1.2) в (1.1) получаем уравнение состояния замкнутой системы — некоторое внешнее воздействие. В результате подстановки (1.2) в (1.1) получаем уравнение состояния замкнутой системы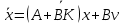 (1.3) (1.3)Устойчивость замкнутой системы (1.3) определяется собственными числами матрицы А + ВК. Система (1.1) называется стабилизируемой при полной обратной связи, если существует матрица К коэффициентов усиления обратной связи такая, что замкнутая система (1.3) асимптотически устойчива. Пара матриц 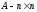 и и 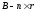 называется невырожденной при выполнении условия называется невырожденной при выполнении условияrank 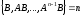 (1.4) (1.4)Невырожденность пары A, В достаточна для стабилизируемости системы (1.1). Пример. Исследовать стабилизируемость системы с уравнением состояния 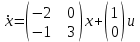 Решение. Пара матриц А и В невырожденна, так как rank 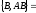 rank rank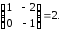 Поэтому система стабилизируема. Пример. Является ли стабилизируемой система с уравнением состояния 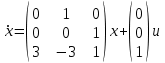 Решение. Составим блочную матрицу 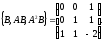 Ее определитель равен минус единице, и поэтому ранг этой матрицы — три. Условие, выраженное равенством (1.4), является только достаточным, но не необходимым для стабидизируемости системы (1.1). Поэтому, если условие (1.4) не выполнено, делать заключение об отсутствии у системы (1.1) свойства стабилизируемости нельзя. НЕОБХОДИМОЕ И ДОСТАТОЧНОЕ УСЛОВИЕ СТАБИЛИЗИРУЕМОСТИ Вопрос о стабилизируемости системы 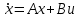 , (2.1) , (2.1)для которой условие (1.4) не выполнено, может быть решен приведением уравнения состояния (2.1) этой системы к канонической форме управляемости. Предположим, что ранг матрицы управляемости rank 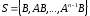 =l (2.2) =l (2.2)равен l. Тогда у этой матрицы есть l линейно независимых столбцов. Обозначим, через  линейно независимые столбцы матрицы S. Пусть матрица Т в качестве первых l столбцов имеет столбцы линейно независимые столбцы матрицы S. Пусть матрица Т в качестве первых l столбцов имеет столбцы  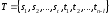 (2.3) (2.3)Остальные п—lстолбцов этой матрицы 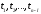 выбираются произвольно, но так, чтобы det выбираются произвольно, но так, чтобы det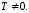 При замене вектора состояния х по формуле 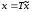 для нового вектора состояния для нового вектора состояния 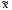 получаем уравнение получаем уравнение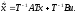 (2.4) (2.4)Матрицы 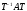 и и 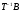 имеют следующую структуру: имеют следующую структуру: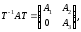 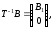 где 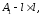 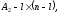 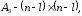 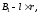 Обозначим вектор-столбец, образованный первыми lкомпонентами вектора состояния  , через , через 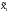 , а вектор-столбец, образованный последующими , а вектор-столбец, образованный последующими 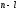 компонентами, через компонентами, через 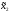 .Тогда уравнение состояния (2.4) с учетом этого обозначения и равенств (2.5) распадается на два: .Тогда уравнение состояния (2.4) с учетом этого обозначения и равенств (2.5) распадается на два: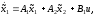 (2.6) (2.6)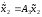 Ранг матрицы rank 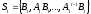 =l (2.7) =l (2.7)равен l. Поэтому подсистема, описываемая первым уравнением (2.6), управляема. На движение подсистемы с уравнением движения 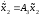 управление не влияет. Она неуправляема. управление не влияет. Она неуправляема.Уравнение (2.6) называют канонической формой управляемости для исходного уравнения состояния (2.1). Необходимым и достаточным условием стабилизируемости линейной стационарной системы (2.1) является отрицательность вещественных частей всех собственных чисел неуправляемой части. Другими словами, отрицательность вещественных частей всех собственных чисел матрицы A3 в канонической форме управляемости (2.4), (2.5) необходима и достаточна для стабилизируемости системы (2.1). Пример. Является ли стабилизируемой система с уравнением состояния 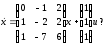 Решение. 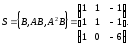 Ранг этой матрицы равен 2. Система не является полностью управляемой. Приведем уравнение состояния к канонической форме управляемости: 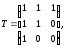 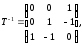 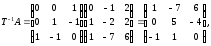 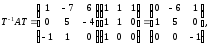 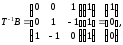 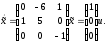 Неуправляемая часть системы 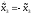 асимптотически устойчива. Система стабилизируема. асимптотически устойчива. Система стабилизируема.РАЗМЕЩЕНИЕ СОБСТВЕННЫХ ЧИСЕЛ И КАЧЕСТВО СТАБИЛИЗАЦИИ Рассмотрим линейную стационарную систему с одним входом и уравнением состояния 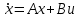 (3.1) (3.1)Пусть для пары матриц 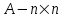 и и 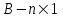 выполнено условие (1.4). Так как матрица выполнено условие (1.4). Так как матрица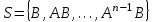 в этом случае квадратная, условие (1.4) эквивалентно неравенству det 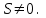 (3.2) (3.2)Системе (3.1) при выполнении (3.2) можно за счет обратной связи вида (1.2) обеспечить любые наперед заданные собственные числа 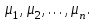 Для этого матрицу К коэффициентов усиления в цепи обратной связи можно выбрать по формуле Для этого матрицу К коэффициентов усиления в цепи обратной связи можно выбрать по формуле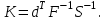 (3.3) (3.3)Здесь столбец dесть разность 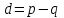 (3.4) (3.4)столбца p, образованного коэффициентами характеристического полинома 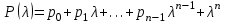 (3.5) (3.5)системы (3.2), и столбца q, образованного коэффициентами полинома, имеющего заданные корни  (3.6) (3.6)Таким образом, 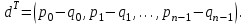 (3.7) (3.7)Матрица Fпостроена из нулей и коэффициентов полинома (3.5), исключая свободный член 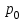 , ,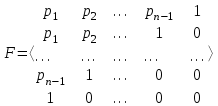 . (3.8) . (3.8)Если для системы с уравнением состояния (3.1) условие (1.4) не выполнено, то любые собственные числа можно обеспечить за счет обратной связи вида и=Кх только управляемой части этой системы. Например, система с уравнением состояния 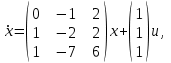 приведенная в предыдущем примере, имеет каноническую форму управляемости 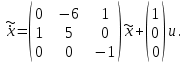 Рассмотрим отдельно управляемую часть 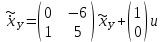 и характеристический полином управляемой части 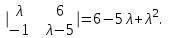 Матрица (3.8) для управляемой части имеет вид 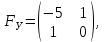 а обратной к ней будет матрица 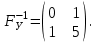 . .Матрица (2.2) для управляемой части является в данном примере единичной 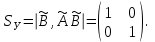 Пусть требуется обеспечить управляемой части собственные числа 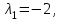 и и 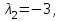 которым отвечает полином которым отвечает полином 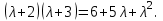 В соответствии с (3.7) 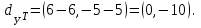 По формуле (3.3) находим 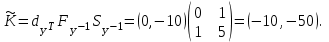 Таким образом, нужная обратная связь имеет вид 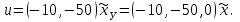 При приведении системы к канонической форме управляемости была выполнена замена переменной 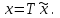 Выполним теперь обратную замену: Выполним теперь обратную замену: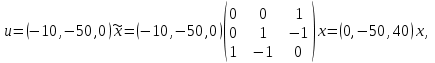 Неуправляемая часть рассмотренной системы имеет собственное число — 1. Обратная связь на это собственное число никак не влияет. Рассмотрим систему с уравнением состояния (1.1), стабилизированную обратной связью (1.2). Такая система описывается уравнением (1.3), и ее собственные движения затухают. Иногда качество стабилизации оценивается временем этого затухания. Обозначим матрицу 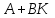 через через 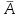 и запишем уравнение собственных движений системы (1.3) в виде и запишем уравнение собственных движений системы (1.3) в виде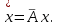 (3.9) (3.9)Если система (3.9) при 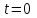 находится в состоянии находится в состоянии 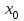 , то для , то для 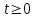 ее состояние меняется по закону ее состояние меняется по закону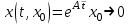 , при , при 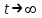 (3.10) (3.10)Зададимся положительным числом ε. Временем затухания собственного движения 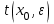 будем называть время, начиная с которого не нарушается неравенство будем называть время, начиная с которого не нарушается неравенство 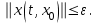 В некоторых случаях качество стабилизации оценивается временем затухания переходного процесса на выходе у=Сх системы (3.9). При этом временем переходного процесса 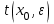 называют время, начиная с которого не нарушается неравенство называют время, начиная с которого не нарушается неравенство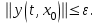 (3.11) (3.11)Неравенство (3.11) эквивалентно неравенству  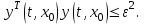 (3.12) (3.12)Подставим в левую часть (3.12) выражение выходного сигнала через вектор состояния 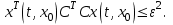 (3. 13) (3. 13)и обозначим симметричную матрицу 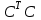 через Q. Тогда временем переходного процесса через Q. Тогда временем переходного процесса 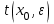 можно назвать время, за которое квадратичная форма можно назвать время, за которое квадратичная форма 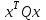 при при 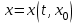 становится и остается в дальнейшем меньше становится и остается в дальнейшем меньше 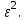 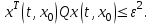 (3.14) (3.14)За счет размещения собственных чисел достаточно далеко влево от мнимой оси можно добиться сколь угодно быстрого затухания переходного процесса при заданной точности, но при этом, прежде чем начнет выполняться неравенство (3.14), фазовый вектор 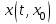 в некоторые моменты может значительно превосходить по норме в некоторые моменты может значительно превосходить по норме 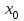 . Поэтому мерой качества процесса стабилизации не всегда можно считать время затухания переходного процесса. Если важно, чтобы за все время переходного процесса левая часть неравенства (3.14) была малой, то целесообразно применять интегральный показатель качества процесса стабилизации . Поэтому мерой качества процесса стабилизации не всегда можно считать время затухания переходного процесса. Если важно, чтобы за все время переходного процесса левая часть неравенства (3.14) была малой, то целесообразно применять интегральный показатель качества процесса стабилизации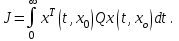 (3.15) (3.15)Чтобы учесть ограничение на допустимый уровень управляющих воздействий 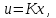 качество процесса стабилизации оценивают величиной интеграла качество процесса стабилизации оценивают величиной интеграла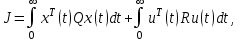 (3.16) (3.16)где Q - положительно полуопределенная, а R - положительно определенная симметричные матрицы. |

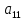 матрицы равен нулю; коэффициент при токе равен С/J, соответственно коэффициент
матрицы равен нулю; коэффициент при токе равен С/J, соответственно коэффициент 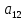 матрицы равен C/J;
матрицы равен C/J; 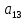 равен нулю.
равен нулю.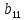 равен нулю; Mc=C*i, соответственно коэффициент при моменте из первого уравнения равен 1/J, отсюда
равен нулю; Mc=C*i, соответственно коэффициент при моменте из первого уравнения равен 1/J, отсюда 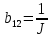 .
.