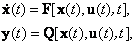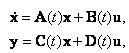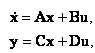АИИК-испр 29-12-2015 (1). Конспект лекций введение. Понятие об автоматических системах
 Скачать 1.74 Mb. Скачать 1.74 Mb.
|
|
Е. Системы аналоговые и дискретные САУ бывают аналогового и дискретного действия в зависимости от характера действия составляющих систему звеньев. Аналоговая система, состоит только из звеньев, выходная величина которых изменяется плавно при плавном изменении входной величины. Система дискретного действия, или дискретная система, — это система, содержащая хотя бы одно звено дискретного действия. Звеном дискретного действия называется звено, выходная величина которого изменяется дискретно, т. е. скачками, даже при плавном изменении входной величины. Скачки выходной величины могут происходить либо при прохождении входной величиной определенных пороговых значений — звено релейного действия, либо через определенный интервал времени — звено импульсного действия. Ж. Адаптивные и неадаптивные системы Адаптивные, или самоприспосабливающиеся, системы обладают способностью приспосабливаться к изменению внешних условий работы, а также улучшать свою работу по мере накопления опыта. Неадаптивные, или, как их еще называют обыкновенные системы такой способностью не обладают. Они имеют постоянную настройку. Область применения адаптивных САУ — это управление объектами, свойства или условия работы которых недостаточно известны или существенно непостоянны. В этих условиях обыкновенная, неадаптивная, система либо будет работать неудовлетворительно, либо потребует постоянного надзора. При рассмотрении процессов в САУ важное значение имеют следующие понятия: устойчивость системы, качество процесса управления и точность управления. Устойчивость — это свойство системы возвращаться в установившееся состояние после того, как она была выведена из этого состояния каким-либо возмущением. Замкнутые САУ, как всякие замкнутые системы, весьма склонны к потере устойчивости, что чаще всего проявляется в возникновении расходящихся колебаний (генерации). Устойчивость является необходимым условием работоспособности любой САУ. Качество процесса управления характеризуется тем, насколько процесс управления близок к желаемому. Количественно оно определяется критериями качества, которые выбираются в соответствии с целью управления. Точность управления характеризуется погрешностью системы в установившихся режимах. Теоремы Ляпунова об устойчивости линеаризованных систем Линейные уравнения реальных автоматических систем получаются всегда в результате той или иной линеаризации, т. е. в результате отбрасывания членов, содержащих вторые и высшие степени, а также произведения отклонений переменных и их производных. Спрашивается: в какой степени устойчивость таких систем с линеаризованными уравнениями соответствует устойчивости реальной системы? Не влияют ли отброшенные члены на устойчивость системы? А. М. Ляпунов доказал ряд оригинальных теорем и предложил ряд методов для исследования устойчивости и поведения динамических систем в различных трудных для обычного анализа случаях. Наибольшей известностью пользуются его методы для исследования нелинейных систем. Приведем содержание (без доказательства) основных теорем Ляпунова об устойчивости линеаризованных систем (или, по выражению Ляпунова, о законности исследования устойчивости по первому приближению). Если характеристическое уравнение линеаризованной системы имеет все корни с отрицательными вещественными частями, то действительная система будет устойчивой (так же, как и линеаризованная), т. е. никакие добавки в виде членов второй и высшей степеней переменных и их производных или их произведений не могут в этом случае «испортить» устойчивость системы. Если характеристическое уравнение линеаризованной системы имеет хотя бы один корень с положительной вещественной частью, то действительная система будет неустойчивой (так же, как и линеаризованная), т. е. никакие добавки в виде членов второй и высших степеней переменных и их производных или их произведений не могут придать устойчивость системе. При наличии нулевых и чисто мнимых корней (хотя бы одного из них) поведение действительной системы не всегда, даже качественно, определяется ее линеаризованными уравнениями. При этом в ряде случаев добавки в виде членов второй и высших степеней переменных и их производных или их произведений могут коренным образом изменить вид динамического процесса в системе. Поэтому по линеаризованным уравнениям, вообще говоря, нельзя судить о том, что происходит на границе устойчивости системы (т. е. при нулевых и чисто мнимых корнях). Однако обычно представляет интерес изучение и проектирование именно таких автоматических систем, которые должны быть устойчивы и достаточно далеки от границы устойчивости. В связи с этим поведение системы при наличии нулевых и чисто мнимых корней вообще не будет рассматриваться, так как этот случай соответствует границе устойчивости, к которой нельзя приближаться при проектировании автоматической системы. Важно то, что в силу первых двух теорем Ляпунова положение границы устойчивости реальной системы определяется по ее линеаризованным уравнениям совершенно точно (если, конечно, система вообще поддается линеаризации). Указанные теоремы Ляпунова являются математическим обоснованием всей линейной теории автоматического регулирования, строго говоря, в технике имеют место не чисто линейные, а именно линеаризованные системы (хотя они и будут для краткости все время дальше называться линейными). При этом очень важно иметь в виду, что эти теоремы Ляпунова справедливы только тогда, когда линеаризация производится по определенному правилу, т. е. когда все нелинейные зависимости имеют (по крайней мере) конечные непрерывные однозначные производные в окрестности точки установившегося процесса. Поэтому эти теоремы не касаются скачкообразных и ломаных зависимостей, и отбрасывание таких существенных нелинейностей, как сухое трение, релейная характеристика, зона нечувствительности и т. п., часто может значительно изменить положение границы устойчивости. Отсюда вытекает практическая важность учета некоторых видов нелинейностей при расчете автоматической системы. Кроме того, отметим, что указанные теоремы Ляпунова касаются только вопроса устойчивости системы, но не вида переходного процесса. На качество переходного процесса и на динамические ошибки системы иногда могут влиять в сильной степени и главного вида нелинейности, отбрасываемые при линеаризации. ОПТИМИЗАЦИЯ АВТОМАТИЧЕСКИХ СИСТЕМ Постановка задачи О 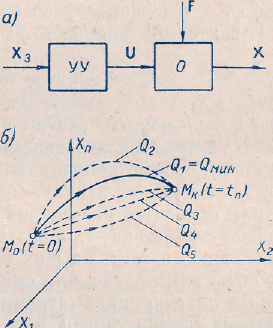 птимальные САУ — это системы, в которых обеспечено оптимальное значение какого-либо основного показателя качества работы системы, называемого критерием оптимальности. Таким критерием оптимальности может быть один из показателей качества переходного процесса (например, его длительность), точность в установившихся режимах, потребляемая мощность, себестоимость продукции и т. п. Рис. 13-1. К задаче оптимального управления В настоящем разделе будет рассмотрена методика синтеза оптимальных САУ. Для решения этой задачи, прежде всего, необходимо иметь возможность выразить количественно критерий оптимальности. Как правило, для определения критерия оптимальности требуется интегрировать во времени какую-либо функцию, величина которой зависит от текущего состояния объекта, т. е. критерий оптимальности является обычно функционалом. Функционал — это величина, значение которой определяется заданием функции. Примером функционала являются интегральные критерии качества, значение которых определяется всей кривой переходного процесса, т. е. функцией хп(t). При этом функционал обычно составляют так, чтобы условием оптимальности системы был минимум этого функционала. В результате задача синтеза оптимальной САУ сводится к синтезу управляющего устройства, обеспечивающего минимум выбранного критерия оптимальности. Математически задачу синтеза оптимального управляющего устройства можно сформулировать следующим образом (рис. 13-1). Имеется объект управления О (рис. 13-1, а), описываемый заданной зависимостью его выходной величины Xот входных величин U и F: X=A0(U, F, t), (13-1) где X – выходная величина, U – управляющее воздействие и F – внешнее возмущение. Эти величины – векторы, содержащие произвольное число составляющих, а А0 — оператор объекта, в общем случае нелинейный. Время tприсутствует в (13-1) в случае нестационарного объекта. Оператор—это закон, определяющий одну функцию по другой. Он может быть задан в виде уравнений, графиков или таблиц. В случае (13-1) оператор А0 символически определяет всю совокупность математических операций, с помощью которых по множеству входных функций U, F и t находится множество выходных функций X, представленных в виде вектора. Часто зависимость (13-1) задают в виде системы дифференциальных уравнений: 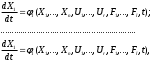 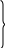 (13-2) (13-2)где 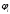 — в общем случае нелинейные функции. — в общем случае нелинейные функции. В векторной форме это выглядит следующим образом: 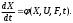 (13-3) (13-3)где  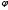 — n-мерный вектор с координатами — n-мерный вектор с координатами 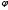 1, ..., 1, ..., 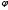 n. n.На управляющие воздействия, входящие в состав вектора U, и на некоторые координаты объекта, входящие в X, практически всегда наложены различные ограничения. Например, к ним относятся насыщение в исполнительных звеньях управляющего устройства, ограничения переменных в объекте управления, определяемые условиями его эксплуатации и конструкцией (ограничение угла поворота заслонок, рулей, движка потенциометра и т. п., ограничение температуры нагрева двигателей, ограничение количества горючего в баках технического устройства). Эти ограничения задаются в виде ряда неравенств: 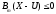 , т = 1,2,..., , т = 1,2,...,  (13-4) (13-4)где Вт — функции или функционалы. В простейшем случае ограничения величины отдельной координаты неравенство (13-4) принимает вид: 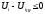 . . или Xi-Xiпр. ≤0 где 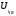 иXiпр.— предельно допустимые значения соответствующих координат. иXiпр.— предельно допустимые значения соответствующих координат.Критерий оптимальности управления задается в виде некоторого функционала Q(X, Х3, U, F, t), зависящего в самом общем случае как от X, U, F и t, так и от задающего воздействия Х3. Обычно он представляет собой интегральную зависимость 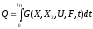 (13-5) (13-5)где 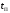 — длительность всего процесса. — длительность всего процесса.Такого типа зависимостями являются, в частности, интегральные критерии качества переходных процессов и среднеквадратичное отклонение случайных процессов. В простейшем, но важном случае, когда G = 1, критерий оптимальности принимает вид: 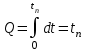 т. е. минимизируется время процесса управления. Системы, в которых это обеспечивается, называются системами, оптимальными по быстродействию. Задача получения оптимального управления заключается в обеспечении такого закона управления U (t), при котором имеет место минимум функционала Q, т. е. Q (X, X3, U , F, t)= min (13-6) Задаче оптимального управления можно дать следующее геометрическое толкование, если воспользоваться фазовым пространством (рис. 13-1, б). Пусть задачей управления объектом является перевод его из начального состояния, соответствующего точке М0(t=0), в состояние, определяемое заданием Х3 и соответствующее точке Мк (t= tп). Перемещение изображающей точки из первого, начального, положения во второе, конечное, происходит под действием управляющих воздействий U1…Ur и может быть осуществлено по различным траекториям (пунктирные линии на рис. 13-1, б) в рамках ограничений (13-4). Каждой траектории соответствует определенное значение критерия оптимальности 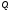 Задача сводится к определению такого управляющего воздействия U(t), при котором процесс перехода X(t) из начального состояния в заданное конечное обеспечивается при минимуме Qс соблюдением условий (13-4). Задача сводится к определению такого управляющего воздействия U(t), при котором процесс перехода X(t) из начального состояния в заданное конечное обеспечивается при минимуме Qс соблюдением условий (13-4).Требование минимизации критерия Q может быть формально заменено требованием минимизации конечного значения одной из координат объекта управления. Для этого в уравнения (13-2) объекта вводится дополнительная координата, которой является функционал Q. Это делается добавлением к уравнениям (13-2) нового уравнения: 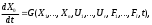 (13-7) (13-7)причем Х0(0) = 0. С учетом (13-5) из (13-7) следует 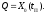 (13-7а) (13-7а)В случае нестационарного объекта можно аналогично устранить время tиз правых частей уравнений (13-2) формальным представлением его в виде еще одной новой координаты 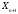 объекта. Для этого к уравнениям (13-2) добавляется уравнение объекта. Для этого к уравнениям (13-2) добавляется уравнение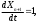 (13-8) (13-8)причем Хп+1(0) = 0. В результате таких преобразований размерность фазового пространства увеличивается на два, т. е. становится равной (п+2), а цель управления формулируется как минимизация значения одной из координат объекта в конечный момент времени. Задача оптимального управления, в которой заданы начальные и конечные точки траектории, — это задача с фиксированными концами. Существуют так называемые задачи со свободным концом траектории, когда конечная точка траектории не задана. Они значительно проще, так как отпадает ограничение на X(tп). Еще большее упрощение задачи получается, если задано время процесса tп, т. е. в случае фиксированного времени процесса. Отметим, что обычно имеется возможность путем изменения критерия оптимальности переходить от задачи с фиксированными концевыми условиями к задаче со свободным концом или от задачи с незаданным временем к задаче с фиксированным временем процесса. Определение оптимального управления U(t) и самого оптимального управляемого процесса X(t) не завершает задачи синтеза оптимальной САУ. Конечной целью синтеза является определение оператора Ауу управляющего устройства, обеспечивающего требуемое оптимальное управление и включающего в себя в самом общем случае выходную величину объекта, внешние воздействия и время: U=AУУ(X, X3, F, t). (13-9) Если одно из внешних воздействий Х3 или F является случайным, критерий оптимальности будет статистическим, например, в виде среднего значения функционала Q. В связи с особенностями математического аппарата в этом случае при дальнейшем изложении вопросов синтеза оптимальных САУ последние разбиты на две следующие группы: оптимальные САУ, находящиеся под действием детерминированных воздействий, оптимальные САУ, находящиеся под случайными воздействиями. Методы нахождения экстремумов функционалов Общим математическим аппаратом, применяемым при синтезе оптимальных САУ, поскольку здесь речь идет о нахождении экстремумов функционалов, является вариационное исчисление, включая как классические вариационные методы, основанные на уравнениях Эйлера — Лагранжа, так и методы, созданные в пятидесятые годы нашего столетия, а именно: динамическое программирование Р. Беллмана и принцип максимума Л. С. Понтрягина. Эти последние методы наиболее удобны для задач оптимального управления, поскольку наличие в этих задачах ограничений существенно усложняет применение классических вариационных методов. Они предполагают применение вычислительных машин, давая программу численного решения задачи на машине. В случае сравнительно простых задач с одним, максимум двумя управляющими воздействиями определение оптимального управления возможно методом прямого поиска путем многократного нахождения процесса на вычислительной машине при вариации управляющего воздействия. В простейшем случае это может быть выполнено на вычислительных машинах непрерывного действия. Для объектов второго порядка оптимальное управление может быть найдено с помощью фазовой плоскости. Рассмотрим метод динамического программирования и принцип максимума. А. Динамическое программирование Этот метод решения вариационных задач предложен американским ученым Р. Беллманом. В основу его положен следующий принцип оптимальности: любой конечный участок оптимальной траектории является тоже оптимальной траекторией, т. е. часть оптимальной траектории от любой промежуточной точки до конца является оптимальной траекторией между этими точками, если считать данную промежуточную точку началом траектории. Сказанное иллюстрируется рис. 13-2. Принцип оптимальности означает, что если траектория 1—2 между точками 0 и К является оптимальной, то оптимальным будет и любой ее конечный участок от произвольной точки iдо точки К. 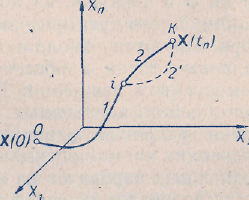 Рис. 13-2. К принципу оптимальности Этот принцип оптимальности не является всеобщим. Он справедлив для систем, у которых оптимальная траектория не зависит от предыстории системы, а целиком определяется исходным ее состоянием. В последнем случае справедливость принципа оптимальности очевидна: если траектория 1—2 оптимальна, обеспечивая минимум критерия, то оптимальна и траектория 2, так как, если оптимальной траекторией между точками iи К оказалась бы какая то другая траектория 2', оптимальной траекторией между точками 0 и К была бы траектория 1—2', поскольку на ней критерий оптимальности имел бы меньшее значение, чем на траектории 1—2, за счет меньшего приращения его на участке 1—2'. Б. Принцип максимума Принципу максимума Л. С. Понтрягина можно дать следующую геометрическую интерпретацию (рис. 13-4, а). Пусть стоит задача о переводе за минимальное время изображающей точки из некоторого начального положения 0 в определенное конечное К. Каждой точке фазового пространства, окружающего точку К, соответствует определенная оптимальная траектория и отвечающее ей минимальное время перехода в эту точку. Вокруг конечной точки можно построить поверхности, являющиеся геометрическим местом точек с одинаковым минимальным временем перехода в эту точку (рис. 13-4, а). Такие поверхности называются поэтому и з о х р о н а м и. Очевидно, что оптимальная по быстродействию траектория из точки 0 в конечную точку К должна быть максимально близка к нормалям изохрон, насколько это позволяют ограничения, налагаемые на координаты объекта управления. 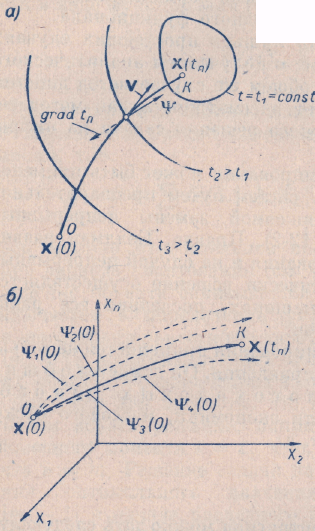 Рис. 13-4. К принципу максимума Действительно, всякое движение вдоль изохрон увеличивает время процесса, так как означает затрату времени без уменьшения отрезка времени, остающегося до момента достижения конечной точки. Математически это условие оптимальности траектории означает, что на протяжении всей траектории скалярное произведение вектора скорости 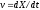 на вектор, обратный градиенту времени перехода в конечную точку, должно быть максимально. на вектор, обратный градиенту времени перехода в конечную точку, должно быть максимально. Если обозначить это произведение через Н, а вектор, обратный градиенту времени перехода, через 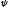 , т. е. , т. е. 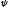 = — grad tп (см. рис. 13-4, а), то это условие можно записать следующим образом: = — grad tп (см. рис. 13-4, а), то это условие можно записать следующим образом: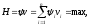 (13-11) (13-11)где 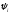 и и 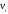 — координаты векторов — координаты векторов 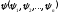 и и 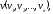 т. е. условием оптимальности является максимум проекции вектора v на направление т. е. условием оптимальности является максимум проекции вектора v на направление 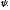 Сформулированное условие оптимальности и есть принцип максимума Л.С. Понтрягина. В общем случае произвольного критерия оптимальности Q (13-5) поверхности постоянного значения этого критерия называются изоповерхностями. Условие оптимальности при этом сохраняется прежним, т. е. в виде максимума скаляра Н, с той только разницей, что в уравнении объекта добавляется новая координата Х0согласно уравнению (13-7), минимизация конечного значения которой определяет цель управления. Практическая методика нахождения оптимального закона управления U(t) и соответствующей оптимальной траектории X(t) не требует определения изоповерхностей. Необходимые для решения задачи векторы 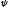 находятся без этого с помощью следующих так называемых сопряженных уравнений, справедливых для оптимальной траектории: находятся без этого с помощью следующих так называемых сопряженных уравнений, справедливых для оптимальной траектории: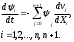 (13-12) (13-12)Здесь X1,Х2, ..., Хп- выходные координаты объекта, а X0 и Xn+1 – дополнительные координаты, выведенные уравнениями (13-7) и (13-8). Уравнения объекта и сопряженные уравнения можно представить в виде уравнений Гамильтона, если ввести в них величину H, учитывая, что, согласно (13-11), 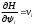 (так как viне зависит от 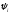 ) и что ) и что 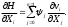 Тогда 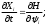 (13-13) (13-13)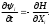 (13-14) (13-14)(Первые уравнения — это уравнения объекта, а вторые — сопряженные уравнения). Соответственно скаляр Н называется гамильтонианом. Наша задача — найти закон управления U(t), дающий в результате совместного решения уравнений объекта (13-13) и сопряженных уравнений (13-14) такую траекторию движения X(t), для которой значения Н в ее точках будут максимальны. Основная сложность здесь заключается в том, что нам известны не все начальные условия задачи: даны начальные значения X(0), но не известны начальные значения 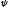 (0) введенной нами вспомогательной величины (0) введенной нами вспомогательной величины 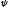 . .Если задаться произвольными начальными значениями 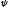 (0) и решить совместно уравнения объекта и сопряженные уравнения, получим оптимальную траекторию, которая пройдет мимо заданной конечной точки К (рис. 13-4, б). Само построение оптимальной траектории при этом может осуществляться путем разделения времени на достаточно малые интервалы (0) и решить совместно уравнения объекта и сопряженные уравнения, получим оптимальную траекторию, которая пройдет мимо заданной конечной точки К (рис. 13-4, б). Само построение оптимальной траектории при этом может осуществляться путем разделения времени на достаточно малые интервалы 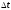 и определения оптимального значения U последовательно для каждого интервала по условию получения максимума значения Н. Оптимальное управление определяется методом последовательных приближений посредством задания последовательно разных начальных значений и определения оптимального значения U последовательно для каждого интервала по условию получения максимума значения Н. Оптимальное управление определяется методом последовательных приближений посредством задания последовательно разных начальных значений 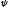 (0) до тех пор, пока не будет получена оптимальная траектория, проходящая через заданную конечную точку. При применении вычислительной машины этот процесс может быть автоматизирован путем организации поиска (0) до тех пор, пока не будет получена оптимальная траектория, проходящая через заданную конечную точку. При применении вычислительной машины этот процесс может быть автоматизирован путем организации поиска 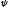 (0) по условию минимизации расстояния до находимых траекторий от заданной конечной точки при одновременной максимизации гамильтониана Н на интервалах (0) по условию минимизации расстояния до находимых траекторий от заданной конечной точки при одновременной максимизации гамильтониана Н на интервалах 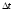 отдельных просматриваемых траекторий. отдельных просматриваемых траекторий.Принцип максимума — необходимое и достаточное условие оптимальности только для линейных объектов. Для общего случая нелинейных объектов он является только необходимым. Пример. Система задана уравнением d2x/dt2=u. (23.19) Требуется найти уравнение преобразовательной части системы u=u(x), чтобы система была оптимальной по быстродействию при переходе ее из произвольного начального состояния в равновесное состояние 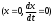 . При этом на управление и наложено ограничение . При этом на управление и наложено ограничение│u│≤1. Обозначив, 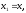 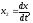 приведем уравнение (23.19) к исходному виду (23.4): приведем уравнение (23.19) к исходному виду (23.4):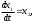 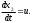 (23.20) (23.20)Функция Н согласно (23.14) и (23.4) здесь имеет вид 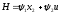 . (23.21) . (23.21)Чтобы определить максимум H по переменной u, надо найти 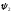 . Для этого воспользуемся уравнениями (23.16), которые в данном случае будут . Для этого воспользуемся уравнениями (23.16), которые в данном случае будут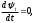 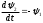 , ,откуда 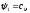 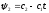 Принцип максимума (23.17), (23.18) с учетом выражения (23.21) и ограничения 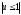 дает даетu=sing 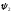 =sing(c2-c1t), =sing(c2-c1t),так как положительный максимум функции H по переменной и будет согласно (23.21) при и = + 1, когда c2-c1t > 0, и при 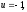 когда когда 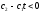 . Поскольку линейная функция . Поскольку линейная функция 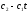 не более одного раза меняет знак, то в оптимальном процессе регулирования будет не более одного переключения с не более одного раза меняет знак, то в оптимальном процессе регулирования будет не более одного переключения с 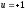 на на 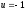 или наоборот. или наоборот.Следовательно, оптимальная по быстродействию система будет релейной, но не обычной релейной, а с особым специальным законом переключения реле по знаку вспомогательной функции 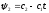 Чтобы представить себе это нагляднее, изобразим процесс на фазовой плоскости. Чтобы представить себе это нагляднее, изобразим процесс на фазовой плоскости.Исключив из уравнений (23.20) dt, получим при 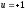 дифференциальное уравнение дифференциальное уравнение 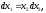 откуда фазовая траектория будет откуда фазовая траектория будет 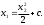 (23.22) (23.22)Аналогично при 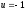 получаем получаем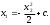 (23.23) (23.23)Таким образом,x1x2 — параболы, симметричные относительно оси абсцисс 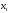 . Процесс должен заканчиваться в начале координат . Процесс должен заканчиваться в начале координат 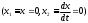 . Поэтому сначала изобразим фазовые траектории (параболы), вливающиеся в начало координат соответственно при . Поэтому сначала изобразим фазовые траектории (параболы), вливающиеся в начало координат соответственно при 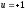 и при и при 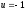 , как показано сплошными линиями на рис. 23.2. , как показано сплошными линиями на рис. 23.2.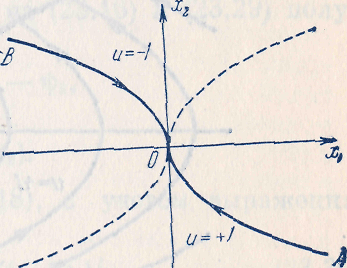 Рис. 23.2. Фазовые траектории Нанесем теперь и все остальные параболы с различными значениями с в формулах (23.22) и (23.23) до точек их вливания в изображенные ранее две ветви параболы, идущие к началу координат. Это и сделано на рис. 23.3. Как видим, из произвольной точки 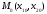 процесс идет по некоторой параболе М0Dпри управляющем сигнале процесс идет по некоторой параболе М0Dпри управляющем сигнале 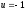 (в другой области было бы и = +1). В точке Dпроисходит переключение реле на сигнал и = +1, после чего процесс идет по параболе DOи заканчивается в точке О за конечное время, которое согласно принципу максима является минимальным из всех возможных для перехода данной системы из состояния (в другой области было бы и = +1). В точке Dпроисходит переключение реле на сигнал и = +1, после чего процесс идет по параболе DOи заканчивается в точке О за конечное время, которое согласно принципу максима является минимальным из всех возможных для перехода данной системы из состояния 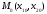 в равновесное состояние 0(0, 0). в равновесное состояние 0(0, 0).Точка переключения реле Dможет находиться в любом месте кривой АОВ. Последняя называется поэтому линией переключения. На ней лежат заключительные отрезки фазовых траекторий, приходящие в начало координат. 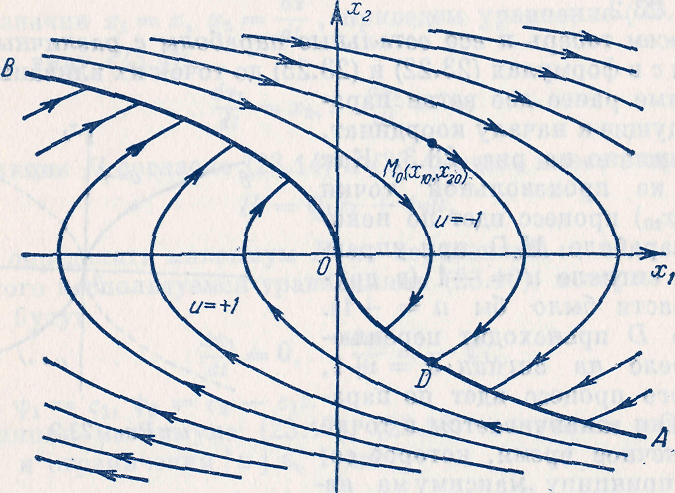 Рис. 23.3. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ АВТОМАТИЧЕСКИХ СИСТЕМ В ПРОСТРАНСТВЕ СОСТОЯНИЙ Современная теория автоматического управления оперирует с векторно-матричными моделями динамических систем. Для получения векторно-матричной модели (ВММ) исследуемая динамическая система представляется в виде “черного ящика” с некоторым числом входных и выходных каналов (рис.1). 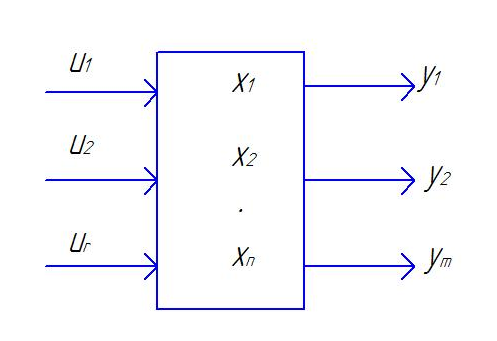 Рис.1. Скалярное представление ВММ Все переменные, характеризирующие систему, можно разделить на три группы: Входные переменные или входные воздействия, генерируемые системами, внешними по отношению к исследуемой системе. Они характеризуются вектром входа. u=[ 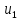 , ,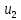 ,….. ,…..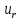 ], r- число входов ], r- число входовВыходные переменные, характеризующие реакцию системы на указанные входные воздействия. Представляются вектором выхода. y=[ 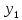 , ,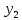 ,…… ,……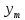 ], m- число выходов ], m- число выходовПромежуточные переменные, характеризующие внутреннее состояние системы, - переменные состояния, представляются вектором x=[ 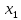 , ,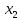 ,….. ,…..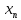 ], n- число переменных состояния. ], n- число переменных состояния.Таким образом, совокупность входов можно рассматривать как один обобщенный вход, на который воздействует вектор входа u, совокупность выходов как вектор y, а совокупность промежуточных координат, характеризующих состояние системы, - в виде вектора состояния x. В общем случае динамическая система в непрерывном виде может быть описана парой матричных уравнений:
В частном случае зависимости могут быть линейными комбинациями переменных состояния xi и входных переменных uq. При этом динамическая система описывается в векторно-матричной форме:
Переход к стационарным моделям позволяет оперировать с коэффициентными матрицами, т.е. со стационарными уравнениями
где |