Учитель
|
Ученик
|
Доска
|
Тетрадь
|
Организационный момент
|
Добрый день! Садитесь!
|
Учащиеся приветствуют учителя и садятся
|
|
|
Актуализация знаний
|
Устная работа.
Задание: Для каждого из графиков, изображенных на рисунке, найдите соответствующую функцию.
|
Выполняют задания устно.
|
Перед уроком учитель заготавливает графики на доске.
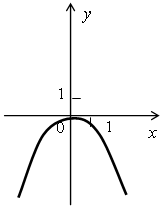
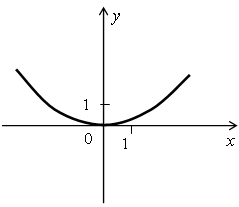
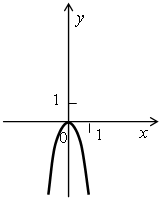
у = -1,7х2; у = -4х2; у = 0,3х2.
|
|
На прошлом уроке были рассмотрены два важнейших преобразования графика функции y=x2.
|
|
|
|
Как получается график функции у= -x2 из графика функции у=x2?
|
График функции у= -x2 получается из графика функции у=x2 с помощью симметрии относительно оси абсцисс.
|
|
|
Как график функции у=аx2 получается из графика функции у=x2?
|
График функции у=аx2 получается из графика функции у=x2 растяжением вдоль оси ординат в а раз при а>1 и сжатием в раз при 0<а<1.
|
|
|
Изучение нового материала
|
Открываем рабочие тетради. Записываем число. Классная работа.
|
Записывают
|
На доске учитель пишет число. Классная работа
|
Число. Классная работа.
|
Сегодня мы рассмотрим еще два важнейших преобразования графика функции у=x2 – построение графиков функций у=ax2+n и у=a(x-m)2.
|
Записывают тему урока
|
Графики функций у=ax2+n и у=a(x-m)2
|
Графики функций у=ax2+n и у=a(x-m)2
|
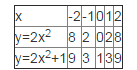
Давайте сравним значения функций у=2х2 и у=2х2+1. Как на удобнее это сделать?
Учитель вызывает одного ребёнка к доске-остальные записывают в тетради.
|
С помощью таблицы
|
|

|
- Как связаны значения функций у=2х2 и у=2х2+1 при одних и тех же значениях аргумента?
|
Отличаются на единицу
|
|
|
- Как можно получить график функции у=2х2+1 из графика функции у=2х2?
|
С помощью параллельного переноса вдоль оси у на одну единицу вверх
|
|
|
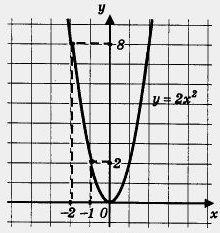
- Давайте построим эти графики и убедимся в этом наглядно.
Дети рисуют графики самостоятельно в тетрадях, потом учитель вызывает одного ребёнка к доске.
|
Строят в тетрадях
|
|

|
- Назовите координаты вершины параболы у=2х2+1.
|
Х=0, у=1
|
|
|
- Назовите ось симметрии параболы у=2х2+1
|
Ось ординат
|
|
|
Итак, запишем правило: Вообще график функции y=ax2+n является параболой, которую можно получить из графика функции y=ax2 с помощью параллельного переноса вдоль оси y на n единиц вверх, если n>0 или на –n единиц вниз, если n<0.
|
Записывают правило в тетрадь
|
Вообще график функции y=ax2+n является параболой, которую можно получить из графика функции y=ax2 с помощью параллельного переноса вдоль оси y на n единиц вверх, если n>0 или на –n единиц вниз, если n<0.
|
Вообще график функции y=ax2+n является параболой, которую можно получить из графика функции y=ax2 с помощью параллельного переноса вдоль оси y на n единиц вверх, если n>0 или на –n единиц вниз, если n<0.
|
Теперь самостоятельно в тетрадях выполняем номер 106(а,б)

|
Решают номер
|
|
|
Проверим, что у нас получилось. Вызывает к доске двух учеников.
|
Схематически изображают параболы.
|

|

|
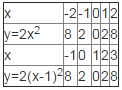
Теперь давайте построим в одной системе координат графики функций у=2х2 и у=2(х-1)2.
Для этого опять составим таблицы значений, только для функции у=2(х-1)2 возьмем значения аргумента на 1 большие, чем для функции у=2х2.
|
Составляют таблицу в тетрадях.
|
|

|
Что можно сказать о значениях функции? Сравните 2 и 4 строки.
|
Они равные
|
|
|
А теперь вспомните, какие значения аргумента мы брали?
|
Для функции у=2(х-1)2 возьмем значения аргумента на 1 большие, чем для функции у=2х2.
|
|
|
- Как можно получить график функции у=2(х-1)2 из графика функции у=2х2?
|
С помощью параллельного переноса вдоль оси х на одну единицу вправо
|
|
|
- Давайте построим эти графики и убедимся в этом наглядно.
|
Строят в тетрадях
|

|

|
- Назовите координаты вершины параболы у=2(х-1)2
|
Х=1
У=0
|
|
|
- Какая ось симметрии у параболы у=2(х-1)2?
|
Ось абсцисс
|
|
|
Итак, запишем правило: Вообще график функции y=a(x-m)2 является параболой, которую можно получить из графика функции y=ax2 с помощью параллельного переноса вдоль оси x на m единиц вправо, если m>0 или на –m единиц вниз, если m<0.
|
Записывают в тетради.
|
Итак, запишем правило: Вообще график функции y=a(x-m)2 является параболой, которую можно получить из графика функции y=ax2 с помощью параллельного переноса вдоль оси x на m единиц вправо, если m>0 или на –m единиц вниз, если m<0.
|
Итак, запишем правило: Вообще график функции y=a(x-m)2 является параболой, которую можно получить из графика функции y=ax2 с помощью параллельного переноса вдоль оси x на m единиц вправо, если m>0 или на –m единиц вниз, если m<0.
|
Самостоятельно в тетрадях выполняем номер 106(в,г)
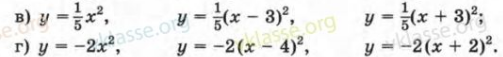
|
|
|
|
Проверим, что у нас получилось. Вызывает к доске двух учеников.
|
Схематически изображают параболы.
|

|

|
А теперь давайте подумаем, как можно из графика функции y=ax2 получить график функции у=a(x-m)2+n?
|
C помощью двух параллельных переносов: сдвига вдоль оси абсцисс на |m| единиц: вправо при m>0 и влево при m<0 и сдвига вдоль оси ординат на |n| единиц: вверх при n>0 и вниз при n<0.
|
|
|
Верно, запишем правило:
Вообще график функции y=a(x-m)2+n является параболой, которую можно получить из графика функции y=ax2 с помощью двух параллельных переносов: сдвига вдоль оси x на m единиц вправо, если m>0 или на –m единиц вниз, если m<0, и сдвига вдоль оси y на n единиц вверх, если n>0 или на –n единиц вниз, если n<0.
|
Записывают в тетрадях
|
Вообще график функции y=a(x-m)2+n является параболой, которую можно получить из графика функции y=ax2 с помощью двух параллельных переносов: сдвига вдоль оси x на m единиц вправо, если m>0 или на –m единиц вниз, если m<0, и сдвига вдоль оси y на n единиц вверх, если n>0 или на –n единиц вниз, если n<0.
|
Вообще график функции y=a(x-m)2+n является параболой, которую можно получить из графика функции y=ax2 с помощью двух параллельных переносов: сдвига вдоль оси x на m единиц вправо, если m>0 или на –m единиц вниз, если m<0, и сдвига вдоль оси y на n единиц вверх, если n>0 или на –n единиц вниз, если n<0.
|
Закрепление
|
1. По данной формуле квадратичной функции ответьте на вопросы:
– каковы вершины параболы;
– куда направлены ветви параболы;
– шире или ýже будет эта парабола по сравнению с у = х2?
а) у = 3х2 – 2; в) у = (х + 4)2 + 5;
г) у = 6 (х + 1,7)2 – 4;
д) у = –1,8 (х – 4)2 – 3.
|
Словесно
Решают самостоятельно в тетрадях.
Отвечают по очереди.
|
|
|
2. Изобразите схематически график функции:
а) у = –3 (х + 1)2 – 2;
б) у = 2,1 (х – 5)2 – 1.
|
Один из учеников читает задачу
|
|
|
Выполните задание самостоятельно в тетрадях. Вызывает двух учеников написать решение на доске.
|
|

|

|
4. На рисунке изображены графики функций:
а) у = –(х – 2)2;
г) у = (х + 1)2 – 3;
в) у = х2 + 1;
г) у = –(х + 2)2 + 3.
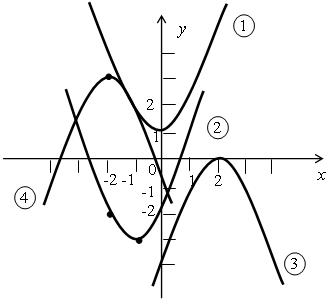
Установите соответствие.
Задание для самостоятельного решения.
Просит одного из учеников назвать получившиеся ответы.
|
Решают самостоятельно в тетрадях.
Потом сверяют.
|
1-в
2-г
3-а
4-б
|
1-в
2-г
3-а
4-б
|
Подведение итогов урока
|
– Что является графиком функций у = ах2 + n и у = а (х – т)2?
|
Парабола
|
|
|
– Как может быть получен график функции у = ах2 + n из графика функции у = ах2?
|
C помощью параллельного переноса вдоль оси y на n единиц вверх, если n>0 или на –n единиц вниз, если n<0.
|
|
|
– Как может быть получен график функции у = а (х – т)2 из графика функции у = ах2?
|
C помощью параллельного переноса вдоль оси x на m единиц вправо, если m>0 или на –m единиц вниз, если m<0.
|
|
|
– – Как может быть получен график функции у = а (х – т)2+n из графика функции у = ах2?
|
C помощью двух параллельных переносов: сдвига вдоль оси x на m единиц вправо, если m>0 или на –m единиц вниз, если m<0, и сдвига вдоль оси y на n единиц вверх, если n>0 или на –n единиц вниз, если n<0.
|
|
|
Постановка домашнего задания
|
Откройте дневники и запишите домашнее задание
|
|
П.12-учить правила, № 107, 111, 116
|
|
 Скачать 218.79 Kb.
Скачать 218.79 Kb.








