Локомотивы. Ремонт узлов локомотива 2. Контрольная работа 1 Дисциплина мдк 04. 02 Ремонт узлов локомотива студент гр. Тэ817

• Название: Контрольная работа 1 Дисциплина мдк 04. 02 Ремонт узлов локомотива студент гр. Тэ817
• Анкор: Локомотивы
• Дата: 11.10.2022
• Размер: 2.6 Mb.
• Имя файла: Ремонт узлов локомотива 2.docx
• Тип: Контрольная работа; #727507
• страница: 2 из 3

Мгновенное повреждение.

Все однотипные объекты в эксплуатации способны выдержать некоторую предельно допустимую нагрузку S_п. Эта способность объектов считается неизменной в течение всего времени эксплуатации, т. е. S_п= const. Иначе говоря, предшествующее использование каждого объекта не влияет на свойства объекта в его последующей эксплуатации. Действующая на объект нагрузка непрерывно, относительно плавно и случайным образом изменяется, как это изображено на рис. 9. Пусть это изменение характеризуется свойствами асимптотической независимости и стационарности.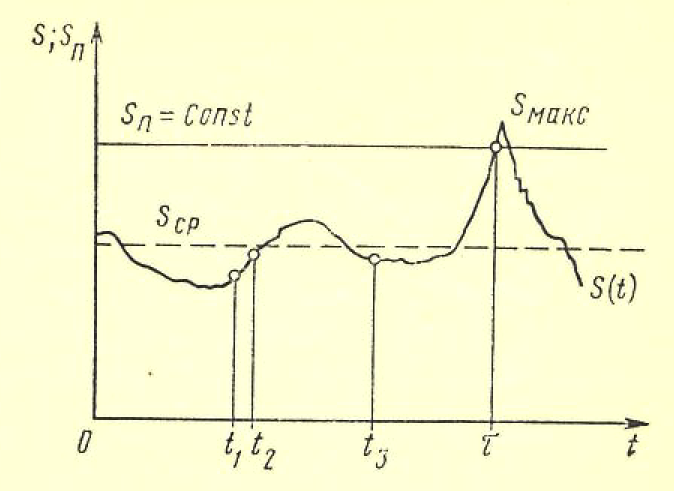



Рис. 9. .Модель возникновения отка-за в схеме мгновенного повреждения

Свойством асимптотической независимости нагрузка S (t) обладает в том случае, если S(t₃) не зависит от S(t₁) при достаточно большой продолжительности времени между моментами t₃ и t₁, т. е. при большой разности (t₃ - t ₁), но S(t₂) явно связана с S(t₁) при малых разностях (t₂ - t ₁ ). Это означает, что моменты «пиковых» нагрузок не могут быть предсказаны заранее.

Отсутствие направленности изменения нагрузки S(t) по мере нарастания времени работы есть свойство стационарности. Средний уровень нагрузки Sсp не изменяется со временем, остается постоянным для всех объектов, находящихся в эксплуатации.

В этих, условиях нагружения возможен случай, когда нагрузка в одном из «пиков» превышает допустимый уровень S_п и при S(t=τ)>S_n наступит отказ объекта. Очевидно, что время до первого пересечения τ будет величиной случайной в силу указанных свойств асимптотическоп независимости и стационарности нагрузки, τ - время безотказной работы объекта, а распределение этого времени в дан-ном случае характеризуется экспоненциальным законом.

Действительно, из исходных положений неизменности свойств изделия следует, что в данном случае функция φ(t)=λ=const, т. е. интенсивность отказов не зависит от времени. Подставляя φ(t)=λ в формулу

общего вида закона, получим дифференциальную и интегральную формы экспоненциального закона распределения: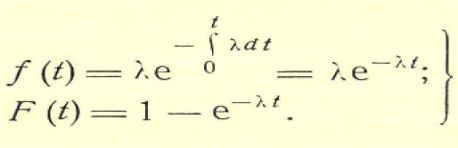



На рис. 10 представлены графики плотности вероятностей и ин-тегрального закона.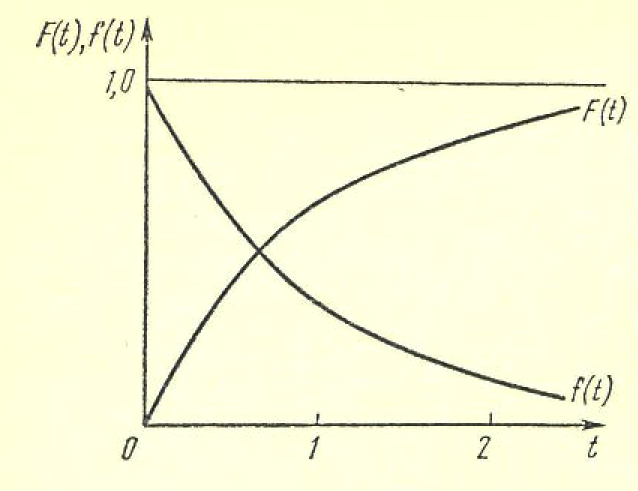



Рис. 10. График экспоненциального закона распределения при λ=1

Модель мгновенных повреждений и полученные формы ее математического вероятностного описания соответствуют некоторым идеализированным представлениям об условиях эксплуатации и свойствах объектов. В теории надежности указаны и другие, более реальные схемы, хорошо описываемые законом экспоненциального распределения.

В практике эксплуатации более распространена ситуация, когда свойства объектов изменяются, т. е. уровень допустимой нагрузки S_n снижается по мере возрастания t. Если такое снижение наступает достаточно быстро после момента t₀《M[τ], то закон распределения по форме изменяется.

Пусть первоначальные свойства нагрузки таковы, что в интервале (0—t₀) нагрузка Sn=Sn.o》S(t)_макс, т. е. вероятность отказа в этом интервале достаточно мала. После момента t₀ за малый интервал (t₀ — t₁) свойства нагрузки ухудшаются до уровня Sn=S_n1, при котором становится ощутимой вероятность повреждения объектов пиками S(t)_макс , как показано на рис. 8. Примером такого процесса может быть внезапное ускорение ухудшения свойств изоляции аппаратов, вызванное повышенными тепловыми нагрузками или увлажнением.

Закон распределения, соответствующий такой модели, можно записать в виде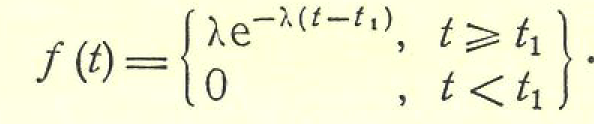



Распределение будет двухпараметрическим (λ; t₁), вид кривой плотности вероятностей см. на рис. 11. Этот закон носит название экспоненциального с порогом чувствительности, поскольку параметр охарактеризует некоторый «порог», до которого объект «не чувствует» нагрузки.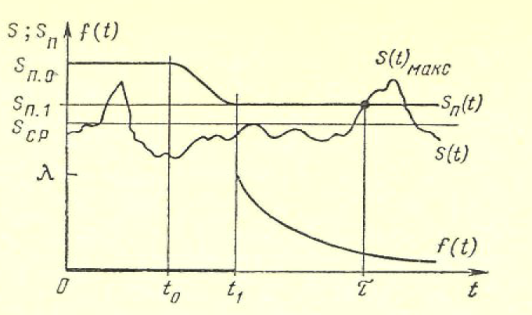


Рис. 11. Модель мгновенного повреждения с порогом чувствительности

В теории надежности отмечается также, что экспоненциальное распределение является предельной статистической моделью времени безотказной работы системы с большим числом последовательно соединенных в структурной схеме надежности элементов. Каждый из элементов не должен оказывать существенно большого влияния на вероятность отказа системы и не обязательно должен иметь экспоненциальное распределение времени безотказной работы.

Рассмотренные модели характерны для конструкционных отказов, когда можно допустить, что все экземпляры достаточно однородны по своим свойствам. Нарушение технологии в большинстве случаев ухудшает качество отдельных экземпляров пли их отдельных групп. Очевидно, что и интенсивность отказов каждой из образовавшихся групп будет различной: изготовленных по нормальной технологии λ₁ при доле их в общей массе ε, изготовленных с нарушениями технологии λ₂ при доле (1—ε).

Плотность распределения времени безотказной работы для всех объектов будет определяться формулой

f(t)=ελ₁e^-λet+(1-ε)λ₂e^-λ₂^t,

выведенной на основе указанных предположений и оценки вероятности отказов групп.

Подводя итог рассмотренной модели мгновенного повреждения, следует заключить, что такая схема формирования потока отказов в идеальном случае отрицает необходимость выполнения профилактических замен элементов или их перио-дического ремонта. Поскольку причиной отказа является внешнее случайное воздействие, а свойства элементов неиз-менны, то замена старого элемента новым не изменяет момента наступления отказа при пике нагрузки. Повышение на-дежности в этом случае можно достигнуть улучшением конструкции, т. е. увеличением уровня свойств изделия S_n или снижением уровня пиков внешних воздействий S(t) макс.
Накапливающиеся повреждения. В исходных положениях этой модели основное место занимает изнашивание, поскольку все элементы реально существующих систем претерпевают в течение периода эксплуатации необратимые изменения. Различают достаточно много видов изнашивания от внешнего трения в зависимости от видов микропроцессов: механическое, коррозионно-механическое, усталостное, эрозионное, абразив-ное, кавитационное и другие. В общем случае под износом понимают результат изнашивания, т. е. остаточные изменения физического состояния объектов не только от трения, но и по другим причинам (например, старение изоляции). Состояние объектов может быть оценено по конфигурации, степени чистоты поверхности и другим стереометрическим показателям, а также по химическому составу, физическим свойствам, напряжению и другим параметрам.

Важной характеристикой является реализация износа, т. е. вид зависимости показателя х_р, характеризующего рабочие свойства изделия, от времени или наработки. Это некоторая случайная функция x_p(t), в общем случае имеющая нелинейный характер. В простейшем случае реализация износа имеет линейный вид

х_p (t)=at+b

графически представленный на рис. 12.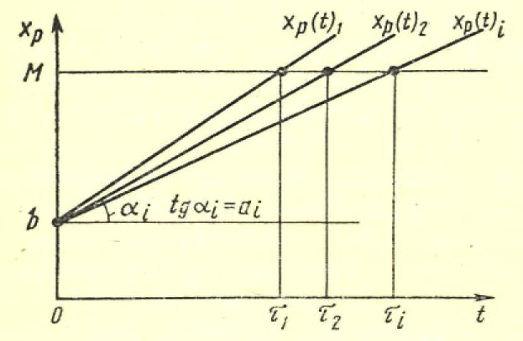



Рис. 12. Линейные реализации износа, характеризующие свойства изделия

Если b=x_p(t=0) - начальное состояние объекта, а= 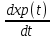- скорость изменения x_p(t), случайно изменяющаяся от объекта к объекту, то τ_i- время безотказной работы ί-го объекта есть величина случайная, определяемая моментом достижения предель-ного состояния х_р(t) = M, т. е. τ_i= .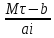

В реальных условиях наблюдаются более сложные зависимости x_p(t), у которых:

начальные свойства могут быть различными, b1≠b2;

средняя скорость изнашивания не одинакова у разных объектов a_1cp≠a_2cp. Возможен и случай, когда a_icp ≠const;

скорость изнашивания у одного объекта случайно меняется в процессе работы, т.е. a = a(t).

Общим для всех этих случаев является то, что в отличие от мгновенных повреждений, приводящих к закону экспоненциального распределения при φ(t)=λ=cons't, интенсивность отказов от износа не остается постоянной с течением времени. Вид реализаций износа отдельных элементов не определяет простейшим образом вида зависимости φ(t), поскольку интенсивность отказов выражает в конечном счете вероятностные связи всего процесса работы всех объектов. Но в целом функция φ(t) безусловно зависит от класса реализации износа, присущего тем или иным объектам.

Изменения интенсивности отказов для наиболее характерных моделей приведены на рис. 13, а формулы φ(t) и соответствующих законов - в табл. 1.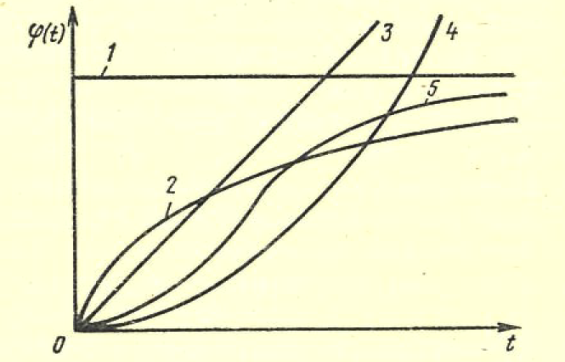



Рис. 13 ( Виды функции интенсивности отказов для разных законов распределений

Таблица 1



Если интенсивность увеличивается пропорционально времени, т. е. φ(t)=λt, то распределение наработки до отказа у таких объектов описывается законом Релея. Износ объектов усиливается по мере нарастания наработки.

Когда интенсивность отказа элементов возрастает со временем, но имеется некоторый предел, то получается закон распределения Эрланга.

Если интенсивность отказов связана с наработкой нелинейно по некоторой степенной зависимости, то имеет место закон распределения наработки до отказа в более общем виде - закон Вейбулла-Гнеденко (см. табл. 1), из которого при r=1 можно получить закон Релея, r=0 - экспоненциальный закон. При r<0 функция интенсивности отказов оказывается убывающей. В теории надежности этот закон применяется довольно часто, так как может быть использован для описания распределения времени безотказной работы многих реальных систем. Особенностью таких систем является наличие большого числа одинаковых или близких по конструкции элементов, находящихся в равных условиях эксплуатации. Отказ любого из этих элементов приводит к отказу системы. Закон распределения Вейбулла-Гнеденко хорошо описывает распределение времени безотказной работы многих элементов радиоэлектронной аппаратуры, шариковых подшипников релейных систем.

В некоторых практически важных моделях функция φ(t) не может быть выражена простой формулой. В теории надежности большое значение при-дается модели, приводящей к гамма-распределению. Эта модель соответствует схеме износа объектов при следующих особенностях:

- средняя скорость изнашивания объектов постоянна;

- начальное качество объектов достаточно однородно.

- скорость нарастания износа подвержена случайным вариациям.

Схема пригодна для случая, когда процессы приработки объектов занимают незначительное время. В процессе работы объекта происходят единичные повреждения Δh, каждое из которых не приводит к отказу, а накопление некоторой их величины вызывает в конечном счете отказ.

Интенсивность отказов гамма-распределения - монотонно возрастающая функция, имеющая некоторый предел (см. рис.13 и таблицу 1)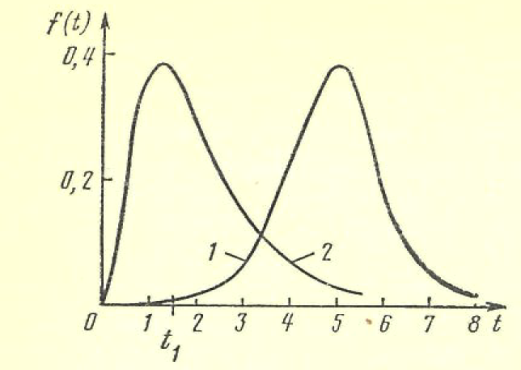



Рис. 14. Плотности вероятностей нормального закона (1) (а = 5, 0—1) и гамма-распределения (2)

Вид функции плотности вероятности (нессиметричная кривая) привелен на рисунке 14.

Увеличение параметра λ гамма-распределения симметрирует график его плотности вероятности относительно ординаты, проходящей через математическое ожиданиe M[t]=a. Дифференциальный закон распределения стремится к виду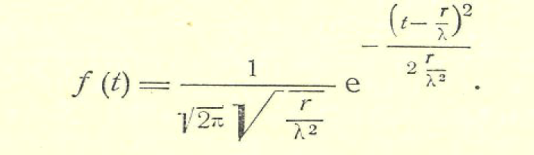



В общем виде это формула известного закона нормального распределения



который широко используется при анализе случайных вели-чин и в теории вероятностей. Теоретическая кривая плотности нормального распределения имеет ветви, симметрично расходящиеся от t=a до t =+∞ и t=-∞. Поскольку в теории надежности t≥0, то применение закона нормального распределения целесообразно в тех случаях, когда вероятность отрицательных значений будет бесконечно мала и не снизит точность расчетов, т. е. Р(t<0).=