Локомотивы. Ремонт узлов локомотива 2. Контрольная работа 1 Дисциплина мдк 04. 02 Ремонт узлов локомотива студент гр. Тэ817
 Скачать 2.6 Mb. Скачать 2.6 Mb.
|
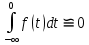 . Это оказывается возможным при . Это оказывается возможным при 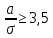 или r≥12. или r≥12.Нормальный закон описывает модель накапливающихся повреждений при однородном качестве объектов, постоянстве средней скорости изнашивания и «переплетении» реализаций износа. Интенсивность отказов при нормальном распределении - возрастающая функция. Значения интенсивности отказов и плотности вероятностей при 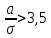 весьма малы па достаточно большом интервале 0-t1. Вероятности отказа в этом интервале также малы (см. рис. 14), что говорит о важности профилактических мероприятий (замен, ремонтов) на небольших уровнях износа (сравните с экспоненциальным законом) . Например, известно, что нормальному закону подчиняется распределение наработки моторно-осевых подшипников (МОП) до отказа, признаками которого являются предельный зазор по износу или разрушение баббитовой заливки. Это вполне соответствует изложенным теоретическим обосно-ваниям. Однако параметры этого закона (средняя наработка до отказа и среднее квадратическое отклонение) существенно зависят от состояния технологии изготовления деталей МОП, сборки этой сборочной единицы при формировании колесно-моторного блока, технического обслуживания, качества смазки и условий токоотвода. Только применение торцовых токо- отводов на электровозах постоянного тока позволило при прочих равных условиях значительно повысить работоспособность МОП. весьма малы па достаточно большом интервале 0-t1. Вероятности отказа в этом интервале также малы (см. рис. 14), что говорит о важности профилактических мероприятий (замен, ремонтов) на небольших уровнях износа (сравните с экспоненциальным законом) . Например, известно, что нормальному закону подчиняется распределение наработки моторно-осевых подшипников (МОП) до отказа, признаками которого являются предельный зазор по износу или разрушение баббитовой заливки. Это вполне соответствует изложенным теоретическим обосно-ваниям. Однако параметры этого закона (средняя наработка до отказа и среднее квадратическое отклонение) существенно зависят от состояния технологии изготовления деталей МОП, сборки этой сборочной единицы при формировании колесно-моторного блока, технического обслуживания, качества смазки и условий токоотвода. Только применение торцовых токо- отводов на электровозах постоянного тока позволило при прочих равных условиях значительно повысить работоспособность МОП.Из прочих моделей отказов по изнашиванию целесообразно остановиться на схеме, которая описывается логарифмически-нормальным распределением. Плотность распределения 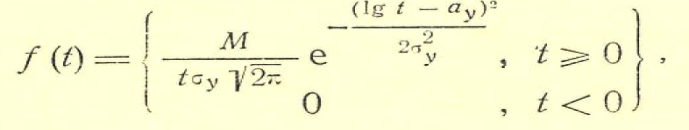 где Интенсивность отказов такого распределения выражается сложной функцией и характерна тем, что при малых t после возрастания наблюдается ее максимум при t = 0, а при t>0 - снижение. Падение интенсивности отказов объясняется тем, что ко времени t = 0 «погибают» экземпляры с высокой скоростью изнашивания, а износ оставшихся в работе нарастает значительно медленнее. В целом такое поведение всей системы выражает ее способность «приспосабливаться» к условиям нагружения, т. е. система имеет свойство тренируемости, приработки. Известно, что накатка шеек валов и осей, поверхности коллекторов увеличивает их способность противостоять изнашиванию, т. е. происходит их упрочнение. Процесс упрочнения есть тоже своеобразная тренировка материала, когда за счет первоначальных деформаций уменьшается износ в последующей эксплуатации. Подобные процессы могут происходить и с объектами, т. е. уменьшение скорости нарастания износа объектов системы возможно не обязательно за счет «гибели» слабых, а именно за счет улучшения свойств в процессе приработки. При эксплуатации коллекторных тяговых двигателей наблюдается такое явление, как «затяжка», заволакивание межламельных промежутков медью. Исследования показали, что распределение наработки до момента, когда затяжка дости-гает предельной величины и подлежит устранению, описыва-ется логарифмически-нормальным законом. Очевидно, что это достаточно хорошо согласуется с физическим процессом образования заволакивания, который особенно интенсивен в начальный период эксплуатации коллектора после обточки, а затем заметно снижается. Рассмотренные модели не охватывают всего многообразия возможных схем развития процессов, отказов. Можно указать на такие важные виды, как релаксационные модели, наложение различных моделей, приводящие к суперпозиции распределений. Математические выражения и физические обоснования этих моделей более сложны, чем в рассмотренных случаях. Кроме моделей, приводящих к непрерывным распределениям, имеется ряд схем, дающих распределения дискретных случайных величин (см. табл. 1). К биноминальному распределению, приводит модель независимых многократно повторяемых испытаний, так называемых испытаний Бернулли. В каждом из них вероятность успеха р, число испытаний п. Подобного рода задачи могут возникнуть при организации приемочного контроля продукции, выборочном обследовании и во многих других случаях. Например, в процессе производства изделий вероятность выпуска дефектной продукции 9%. Продукция принимается большими партиями, из которых случайным образом для контроля выбирается 20 деталей. Партия принимается, если в ней не более двух дефектных деталей. Какова вероятность принятия партии при таком контроле? В данном случае х-2, п = 20, р = 0,09 и по формуле -из табл. 1 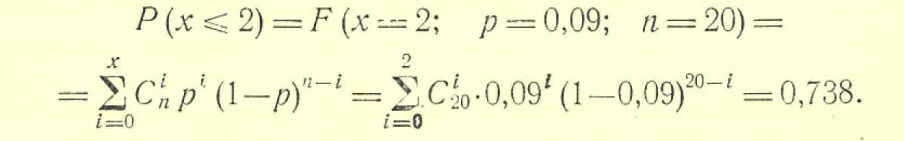 Распределение Пуассона используют при статистической модели, в которой события происходят независимо друг от друга с некоторой постоянной интенсивностью. Оно позволяет найти вероятность появления заданного числа событий в равные промежутки времени или пространства. Такой вид распределения имеют, например, повторности обточек коллекторов и круговых огней на коллекторах тяговых двигателей за некоторый период эксплуатации. Рассмотрение идеализированных моделей показало, что они охватывают достаточно большой круг возможных схем развития процессов возникновения отказов. Очень важен тот факт, что каждая модель может быть описана своим законом распределения времени безотказной работы (наработки до отказа). Знание таких законов необходимо для решения мно-гих практических задач надежности ТПС. |
