Финансовый менеджмент (). Контрольная работа 1 по дисциплине Финансовый менеджмент выполнена по методике Ф. А. Красина Финансовый менеджмент
 Скачать 190 Kb.
|
|
Факультет дистанционного обучения Томский государственный университет систем управления и радиоэлектроники (ТУСУР) Кафедра экономики Контрольная работа № 1 по дисциплине «Финансовый менеджмент» выполнена по методике Ф.А. Красина «Финансовый менеджмент» Вариант № 2 Выполнила студентка ФДО ТУСУР гр.: *********** специальности ***************** ********************************. ******************** Задание 1. Клиент поместил в банк 100 тыс. руб. под простую процентную ставку 15% годовых. Какая сумма будет на его счете через: а) 7 месяцев; б) три года; в) 3 года 3 месяца? При расчете используйте формулу обычного процента с приближенным числом дней. Решение: Воспользуемся формулой F = P(1 + n * r), где F – наращенная сумма, Р – вложенная сумма, n - количество лет, r – простая процентная ставка. а) Р = 100 000; n = 7/12 = 0,58; r = 15%. Найдем F: F = 100 000 (1 + 0,58 * 0,15) = 108 700 руб. б) Р = 100 000; n = 3; r = 15%. Найдем F: F = 100 000 (1 + 3 * 0,15) = 145 000 руб. в) Р = 100 000; n = 3,25; r = 15%. Найдем F: F = 100 000 (1 + 3,25 * 0,15) = 148 750 руб. Ответ: а) F =108,7 тыс.руб.; б) F =145 тыс.руб.; в) F =148,75 тыс.руб. Задание 2. Предприниматель хочет получить ссуду в 600 тыс.руб. на полгода. Банк предоставляет ссуду на условиях начисления простых учетных процентов по ставке 26% годовых. Какую сумму предприниматель будет должен банку? Решение: Для решения этой задачи воспользуемся формулой наращения капитала по простой ставке ссудного процента: F = P (1 + r * t/T), где t – продолжительность финансовой операции в днях; Т – количество дней в году. Используя обыкновенный процент с приближенным числом дней, получим: t = 6 * 30 = 180 дней. P = 600 000; t = 180 дн.; T = 360 дн.; r = 26%. F = 600 000 ( 1 + 0,26 * 180/360) = 678 000 руб. Ответ: предприниматель должен будет сумму к погашению – 678 тыс.руб. Задание 3. В банк вложены деньги в сумме 80 тыс.руб. на полтора года под 30% годовых с ежеквартальным начислением сложных процентов. Определите доход банка в этой финансовой операции. Решение: Для решения задачи используем формулу: F = P (1 + r)n Р = 80 000; r = 30%; n = 540/360 = 1,5. F = 80 000 (1 + 0,30)1,5 = 80 000 * 1,48223 = 118578,23 руб. 118578,23 – 80 000 = 38 578,23 руб. Ответ: доход банка в этой финансовой операции составит 38 578,23 руб. Задание 4. За взятые в долг деньги под сложную процентную ставку 34% годовых должник обязан уплатить кредитору 1 августа 2002г. 400 тыс.руб. Какую сумму необходимо иметь должнику, если он вернет деньги: а) 1 января 2002г.; б) 1 января 2003 г.; в) 1 августа 2003г.? Решение: Для начала найдем приведенную вложенную сумму по формуле: P = F/(1 + r)n, где n – количество лет. Р = 400 000/(1 + 0,34)1 = 400 000/1,34 = 298 507,46 руб. а) На 1 января 2002 г. должнику необходимо иметь сумму: F = P(1 + r)w+f = 298 507,46 (1 + 0,34)0,42 = 337 550,85 руб. б) На 1 января 2003г. должнику необходимо иметь сумму: F = 298 507,46(1 + 0,34)1,42 = 452 318,14 руб. в) На 1 августа 2003г. должнику необходимо иметь сумму: F = 298 507,46 (1 + 0,34)2 = 536 000 руб. Ответ: а) F = 337 550,85 руб; б) F = 452 318,14 руб; в) F = 536 000 руб. Задание 5. Определите дисконтированную сумму при учете 100 тыс.руб. по простой и сложной учетной ставкам, если годовая ставка равна 18% годовых и учет происходит за 30 дней, 180 дней, 1 год, 3 года, 5 лет. Полагать год равным 360 дней. Решение: Применяя формулу P = F(1 – n * d) для простой учетной ставки и формулу P = F(1 – d)n для сложной учетной ставки при F = 100 000 руб., d = 0,18 и различных n, получим:
Задание 6. Банк выдает ссуду под сложную процентную ставку 20% годовых. Какую простую годовую процентную ставку должен установить банк, чтобы его доход не изменился, если начисление процентов происходит: а) по полугодиям; б) каждые 2 месяца; в) каждую неделю. Решение: а) По формуле: 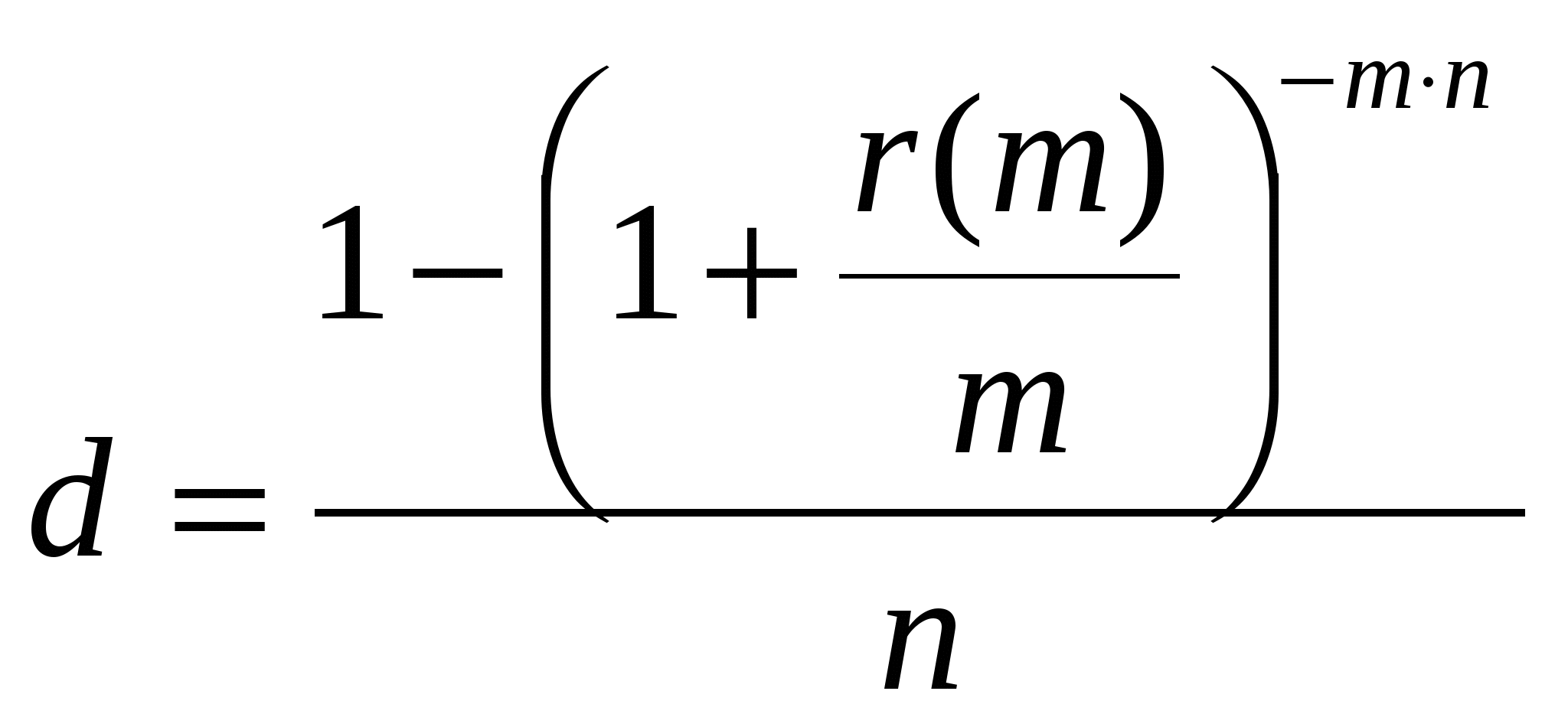 ,где n = 6/12 = 0,5; r = 0,2 находим требуемую величину простой учетной ставки: 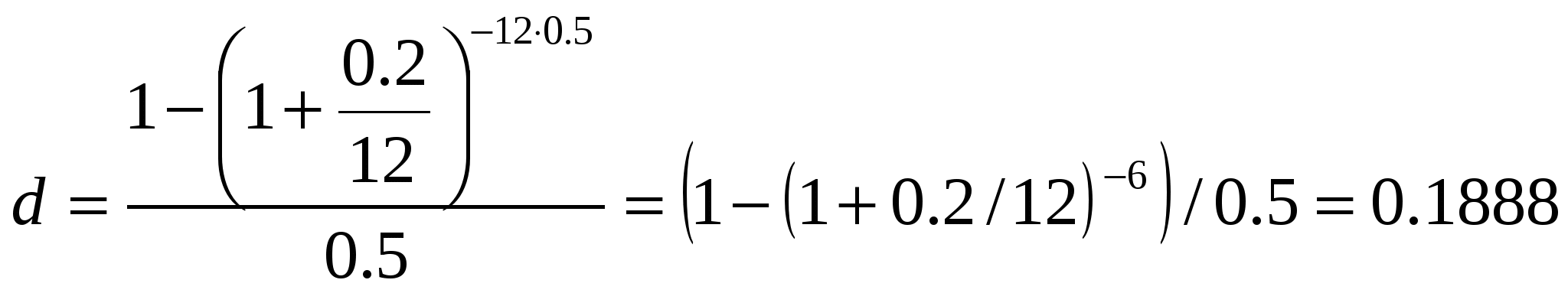 Таким образом, искомое значение простой учетной ставки составляет 18,88% годовых. б) n = 0,17; r = 0,2 находим требуемую величину простой учетной ставки:  Следовательно, искомое значение простой учетной ставки составляет 19,5% годовых. в) n = 0,02; r = 0,2 находим требуемую величину простой учетной ставки:  Следовательно, искомое значение простой учетной ставки составляет 19,8% годовых. Ответ: а) 18,88%; б) 19,5%; в) 19,8%. Задание 7. Номинальная процентная ставка, компенсирующая при наращении инфляцию, составляет 48% годовых. Определите инфляцию за квартал, если начисление сложных процентов осуществляется каждый месяц. Решение: Приравняем годовой индекс инфляции к множителю наращения за год. Полагая, r12 = 0,48, получим: I р1 = (1 + r12/12)12 = (1 + 0,48/12)12 = 1,601 Поэтому индекс инфляции за квартал (0,25 года) составит: Iр0,25=  1,2653.Таким образом, темп инфляции за квартал в среднем равен 26,53%. Ответ: темп инфляции за квартал равен 26,53%. Задание 8. Анализируются два плана накопления денежных средств по схеме аннуитета постнумерандо: 1)класть на депозит 20 тыс. руб. каждые полгода при условии, что банк начисляет 18% годовых с полугодовым начислением процентов; 2) делать ежегодный вклад 42 тыс. на условиях 19% годовых при ежегодном начислении сложных процентов. Какая сумма будет через 10 лет при реализации каждого плана? Решение: План 1: FVpst = A * FM3(r,n), где А – величина каждого денежного поступления; FVpst – будущая стоимость аннуитета постнумерандо. Входящий в формулу множитель FM3(r,n) называется коэффициентом наращения аннуитета и находится по формуле: FM3(r,n) = ((1 + r)n – 1)/r ; n = 20, r = 18% = 0,18/2 = 0,09. FM3(r,n) = ((1 + 0,09)20 – 1)/0,09 = 51,1601. Тогда: FVpst = 20000 * 51,1601 = 1023202 руб. План 2: FVpst = A * FM3(r,n), где n = 10, r = 19%. FM3(r,n) = ((1 + 0,19)10-1)/0,19 = 24,7089. Тогда: FVpst = 42000 * 24,7089 = 1037773,8 руб. Ответ: 1) FVpst = 1023202 руб.; 2) FVpst = 1037773,8 руб. Задание 9. Банк предлагает ренту постнумерандо на 10 лет с ежеквартальной выплатой 4 тыс.руб. Годовая процентная ставка 32%, сложные проценты начисляются ежеквартально. По какой цене можно приобрести эту ренту, если выплаты начнут осуществляться: а) немедленно; б) через 4 года? Решение: а) Используем формулу: PVpst = A * FM4(r,n), где А – величина каждого денежного поступления, FM4(r,n) – коэффициент дисконтирования ренты. При r = 32/4 = 8%; n = 10*4 = 40. FM4(r,n) =  = 11,925.Найдем PVpst = 4000 * 11,925 = 47700 руб. б) Используя формулу PVpst = A * FM2(r,h) * FM4(r,n), считая квартал базовым периодом, при h = 4*4 = 16. Найдем: FM2(r,h) = 0,2919. PVpst = 4000 * 0,2919 * 11,925 = 13923,63 руб. Ответ: а) PVpst = 47700 руб., б) PVpst = 13923,63 руб. Задание 10. Для создания фонда фирма вкладывает ежегодно в банк по 240 тыс.руб. под годовую ставку 20%. Определите сумму, накопленную в фонде через 5 лет, если начисление процентов – полугодовое и: а) взносы делаются в конце года; б) взносы делаются равными долями в конце квартала. Решение: Воспользуемся формулой: FVpst= 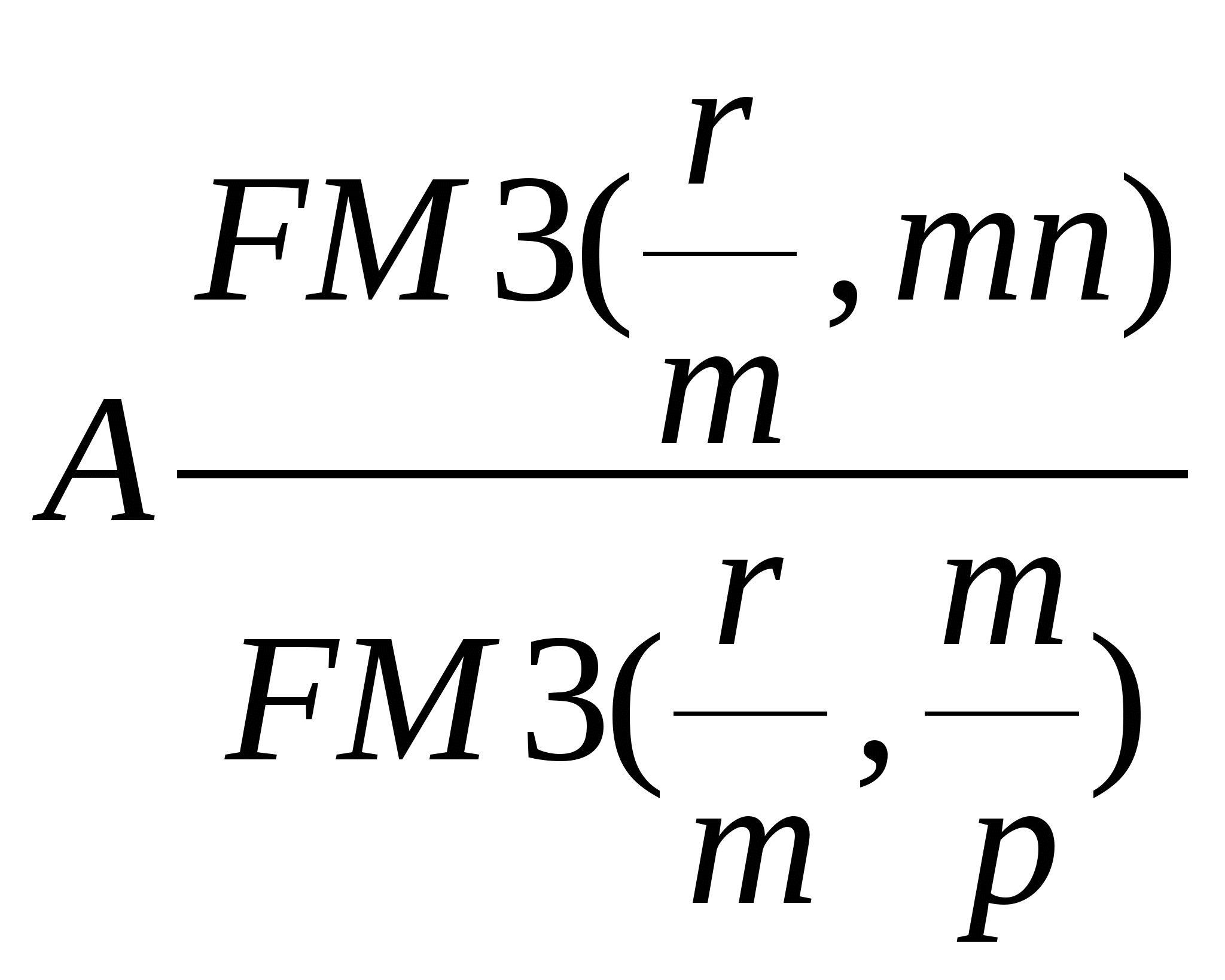 а) А = 240 000 руб. r = 20%, n = 5, m = 2, p =1. Найдем: FM3(r/m,mn) = FM(10,10) = ((1 + 0,1)10 – 1)/0,1 = 15,937. FM3(r/m,m/p) = FM3(10,2) = ((1 + 0,1)2 – 1)/0,1 = 2,1. FVpst = 240000 * 15,937/2,1 = 1821371,43 руб. б) А = 60 000 руб. r = 20%, n = 5, m = 2, p = 4. Найдем: FM3(r/m,mn) = FM(10,10) = ((1 + 0,1)10 – 1)/0,1 = 15,937. FM3(r/m,m/p) = FM3(10;0,5) = ((1 + 0,1)0,5 – 1)/0,1 = 0,488. FVpst = 60000 * 15,937/0,488 = 1959467,21 руб. Ответ: а) FVpst =1821271,43 руб. б) FVpst =1959467,21 руб. Задание 11. В течении 3 лет на счет в банке ежедневно будут поступать одинаковые платежи, каждый год составляя в сумме 150 тыс.руб. Определите сумму, накопленную в конце срока при использовании процентной ставки 18% годовых, если начисление сложных процентов осуществляется по полугодиям. Решение: Полагаем n = 3, m = 2, r = 18%. Поскольку платежи поступают достаточно часто, будем считать, что они поступают непрерывным образом. Тогда воспользуемся формулой: 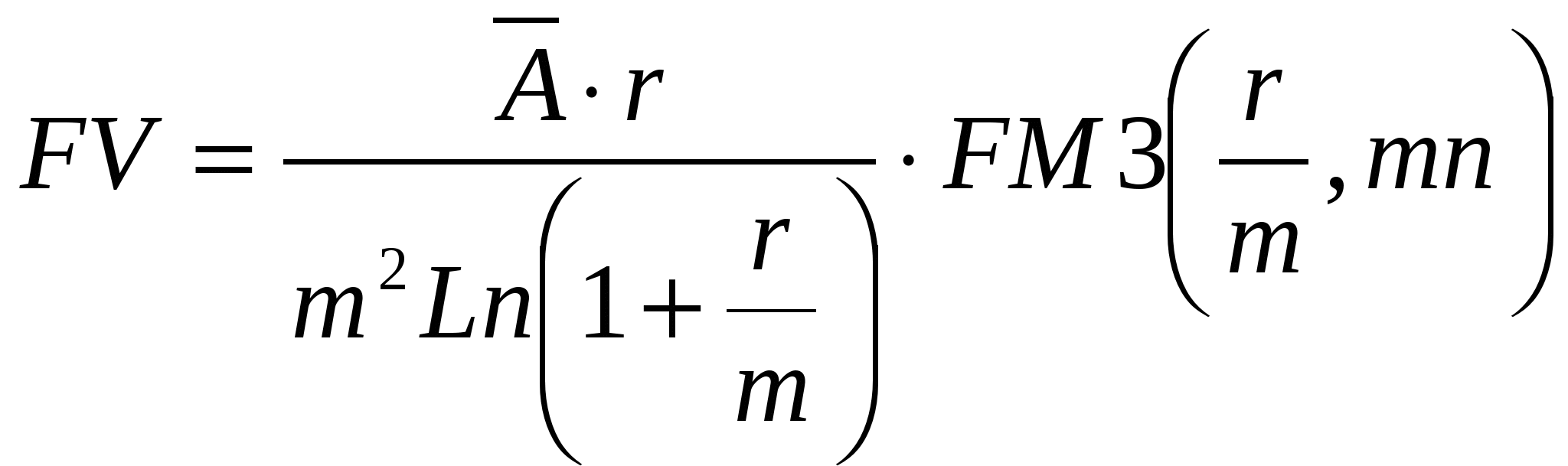 , для определения наращенной суммы непрерывного аннуитета при  руб.  руб.Ответ: FV = 589,25 тыс.руб. Задание 12. По условиям контракта на счет в банке поступают в течение 6 лет в начале года платежи. Первый платеж равен 50 тыс.руб., а каждый последующий по отношению к предыдущему увеличивается на 12%. Оцените этот аннуитет, если банк начисляет сложные проценты из расчета 20% годовых. Решение: Поскольку ежегодно платежи увеличиваются в 1.12 раза (на 12%), то денежный поток представляет собой переменный аннуитет постнумерандо с постоянным относительным изменением его членов. Поэтому для оценки аннуитета воспользуемся формулой: FVpre = FVpst(1 + r). Полагая А = 50000 руб., n = 6, r = 20% (0,2) и q = 1,12 получим:  тыс.руб.FVpre = 637,5 * (1 + 0,2) = 765тыс.руб. Ответ: FVpre = 765 тыс.руб. Задание 13. Условно – постоянные расходы компании равны 12 млн. руб., отпускная цена единицы продукции – 16 тыс. руб., переменные расходы на единицу продукции – 10. Рассчитайте: а) критический объем продаж в натуральных единицах; б) объем продаж, необходимый для достижения прибыли в 3 млн.руб. Как изменятся значения этих показателей, если: 1) условно-постоянные расходы увеличатся на 15%; 2) отпускная цена возрастет на 2 тыс.руб.; 3) переменные расходы возрастут на 10%; 4) изменятся в заданной пропорции все три фактора? Решение: а) По формуле:  найдем критический объем продаж в натуральных единицах. = 12000/(16 – 10) = 2000 единиц.б) По формуле:  найдем объем продаж, необходимый для достижения прибыли в 3 млн.руб. = 12000 + 3000/(16 – 10) = 15000/6 = 2500 единиц.1) Условно-постоянные расходы увеличатся на 15%, то есть FC = 12000 * 1,15 = 13800 тыс.руб.  единиц единиц2) Отпускная цена возрастет на 2 тыс.руб., т.е. Р = 16 + 2 = 18 тыс.руб.  единиц единиц3) Переменные расходы возрастут на 10%, т.е. V = 10*1,1 = 11 тыс.руб.  единиц единиц4) Изменятся в заданной пропорции все три фактора, т.е. FC = 12000*1,15 = 13800 тыс.руб. Р = 16 + 2 = 18 тыс.руб. V = 10 * 1,1 = 11 тыс.руб.  единиц единицОтвет: а) = 2000 ед., б) = 2500 ед., 1)  ед.,  ед.2)  ед.,  ед.3)  ед.,  ед.4)  ед.,  ед.Задание 14. Компания Х имела 1 июня остаток денежных средств на расчетном счете в сумме 10000 руб. Компания производит продукцию со следующими удельными показателями: - затраты сырья – 20 руб.; - оплата труда – 10 руб.; - прямые накладные расходы – 10 руб. Известно, что объемы производства и продаж в натуральных единицах составил:
Требуется: составить прогноз движения денежных средств до конца 2001 г., если имеется следующая информация: 1) цена реализации – 80 руб.; 2) все прямые расходы оплачиваются в том же месяце, когда они имели место; 3) продажа продукции осуществляется в кредит, период кредита – 1 месяц; 4) в июле компания приобрела новый станок за 20000 руб., оплата за станок – в октябре; 5) постоянные накладные расходы оплачиваются ежемесячно в сумме 1900р. Решение: Расчет себестоимости
Денежный поток
Задание 15. Эксперты компании Х составили сводные данные о стоимости источников в случае финансирования новых проектов (%):
Целевая структура капитала компании составляет: - привилегированные акции – 15%; - обыкновенный акционерный капитал – 50%; - заемный капитал – 35%. Требуется: рассчитать значение WACC для каждого интервала источника финансирования. Решение:
1) Расчет WACC для диапазона от 0 до 250: WACC(0-250) = 0,35*7 + 0,15*15 + 0,5*20 = 14,7%; 2) Расчет WACC для диапазона от 250 до 500: WACC(250-500) = 0,35*7 + 0,15*15 + 0,5*22 = 15,7%; 3) Расчет WACC для диапазона от 500 до 750: WACC(500-750) = 0,35*8 + 0,15*17 + 0,5*23 = 16,85%; 4) Расчет WACC для диапазона от 750 до 1000: WACC(750-1000) = 0,35*9 + 0,15*18 + 0,5*24 = 17,85%; 5) Расчет WACC для диапазона свыше 1000: WACC(свыше 1000) = 0,35*12 + 0,15*18 + 0,5*26 = 19,9%;
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||