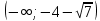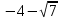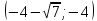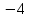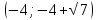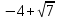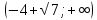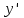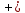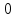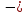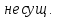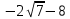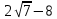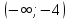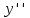Математика. КР. Контрольная работа 1 Вариант 6 Решить систему линейных алгебраических уравнений тремя способами
 Скачать 341.39 Kb. Скачать 341.39 Kb.
|
|
46. Вычислить пределы непосредственно. В случаях 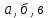 проверить по правилу Лопиталя проверить по правилу Лопиталя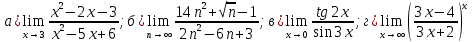 Решение: 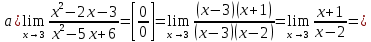 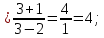 Проверка: 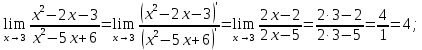 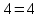 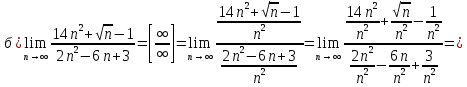 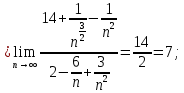 Проверка: 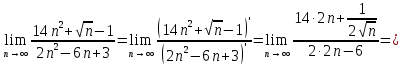 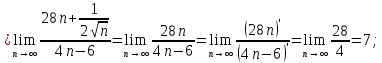 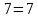 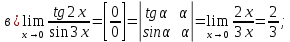 Проверка: 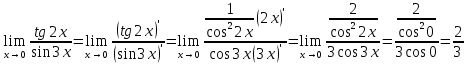 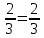 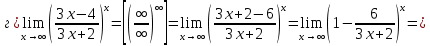 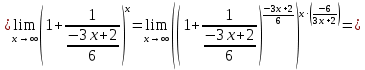 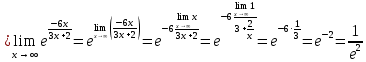 Использован второй замечательный предел 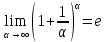 Ответ: 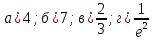 56. Задана функция 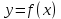 . Найти точки разрыва функции, если они существуют. Сделать чертеж. . Найти точки разрыва функции, если они существуют. Сделать чертеж.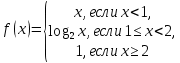 Решение: Функция является непрерывной на каждом из промежутков, поэтому подозрительными на разрыв являются точки 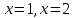 Исследуем на непрерывность точку 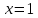 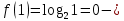 функция определена в этой точке функция определена в этой точке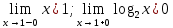 Односторонние пределы конечны и различны, значит, функция имеет разрыв первого рода. Скачок равен 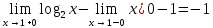 Исследуем на непрерывность точку 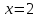 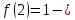 функция определена в этой точке функция определена в этой точке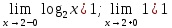 Односторонние пределы конечны и равны, значит, существует общий предел. Предел функции в точке равен значению данной функции в данной точке. Следовательно, функция непрерывна в точке 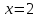 по определению непрерывности функции в точке. по определению непрерывности функции в точке.Следовательно, функция непрерывна на всей числовой прямой, кроме точки 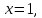 в которой она терпит разрыв первого рода со скачком равным в которой она терпит разрыв первого рода со скачком равным 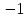 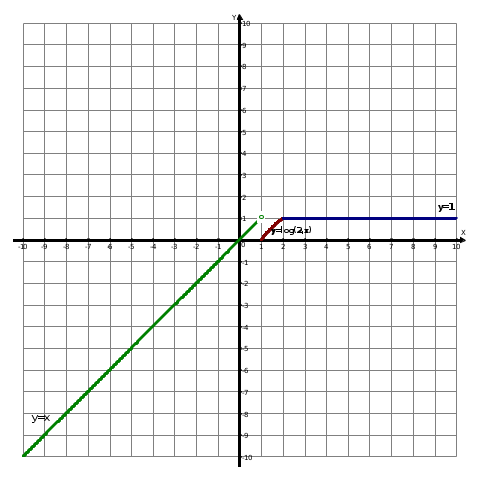 Ответ: функция непрерывна на всей числовой прямой, кроме точки 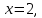 в которой она терпит разрыв первого рода со скачком равным в которой она терпит разрыв первого рода со скачком равным 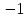 66. Найти производные 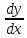 данных функций данных функций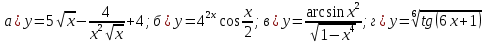 Решение: 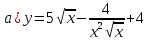 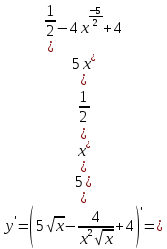 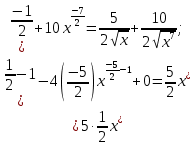 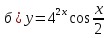 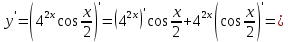 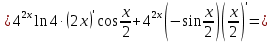 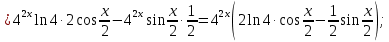 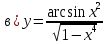 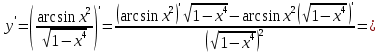 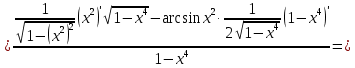 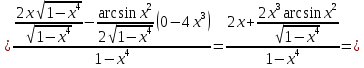 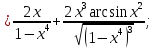 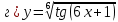 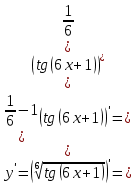 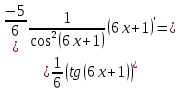 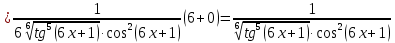 Ответ: 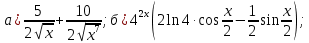 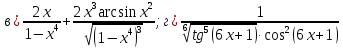 76. Найти производную 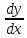 показательно-степенной функции показательно-степенной функции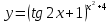 Решение: 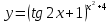 Прологарифмируем левую и правую часть заданной функции 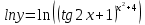 По свойствам логарифмов в правой части полученного равенства степень подлогарифмической функции выносим перед логарифмом 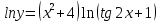 Дифференцируем левую и правую часть равенства. Слева берем производную как от сложной функции (так как 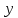 - это функция от переменной - это функция от переменной 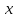 ), а справа - как производную произведения ), а справа - как производную произведения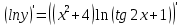 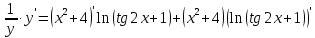 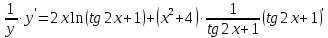 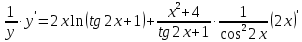 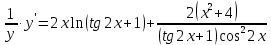 Тогда 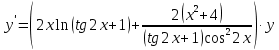 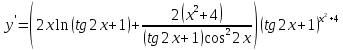 Ответ: 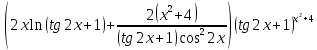 86. Исследовать функцию методом дифференциального исчисления и схематично построить ее график 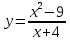 Решение: 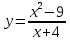 Область определения Функция определена во всех точках, кроме тех, где знаменатель обращается в нуль 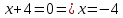 Область определения функции, следующая 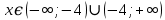 Точки пересечения с осями координат Пусть 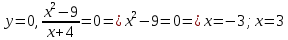 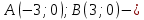 точки пересечения с осью точки пересечения с осью 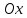 Пусть 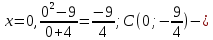 точки пересечения с осью точки пересечения с осью 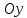 Четность, нечетность, периодичность 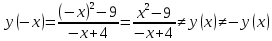 Следовательно, функция не является ни четной, ни нечетной. Функция общего вида, непериодическая Вертикальные асимптоты Функция определена всюду, кроме 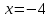 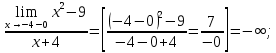 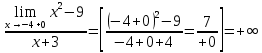 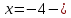 вертикальная асимптота вертикальная асимптотаНаклонные асимптоты. 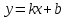 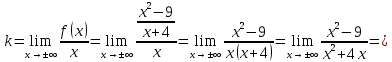 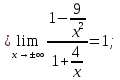 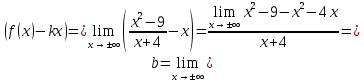 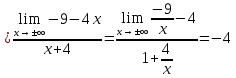 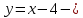 наклонная асимптота наклонная асимптотаТочки экстремума, интервалы возрастания, убывания Вычислим 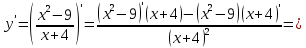 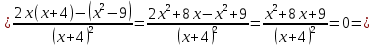 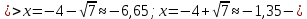 критические точки критические точки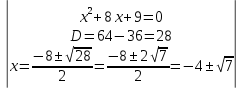 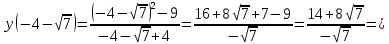 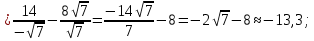 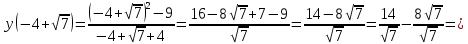 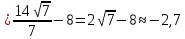
При переходе через критическую точку 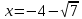 производная меняет знак c плюса на минус. Следовательно, в точке производная меняет знак c плюса на минус. Следовательно, в точке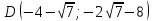 функция имеет максимум. функция имеет максимум.При переходе через критическую точку 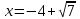 производная меняет знак c минуса на плюс. Следовательно, в точке производная меняет знак c минуса на плюс. Следовательно, в точке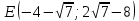 функция имеет минимум. функция имеет минимум.Точки перегиба, интервалы выпуклости, вогнутости 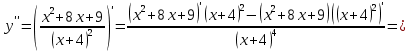 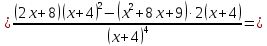 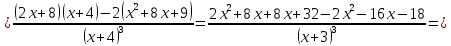 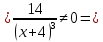 точек перегиба нет точек перегиба нет
Используя полученные данные, строим график функции. 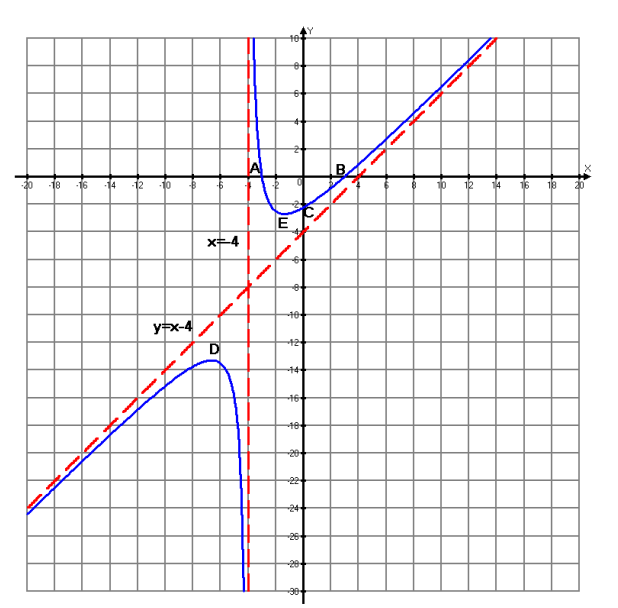 96. Найти частные производные функции 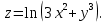 Показать, что Показать, что 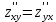 Решение: 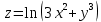 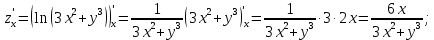 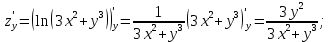 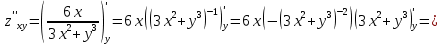 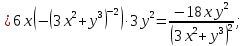 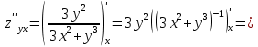 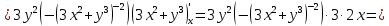 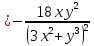 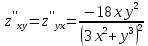 Ответ: 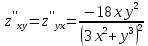 106. Найти наименьшее и наибольшее значения функции в замкнутой области 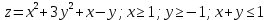 Решение: Сделаем чертеж замкнутой области 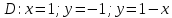 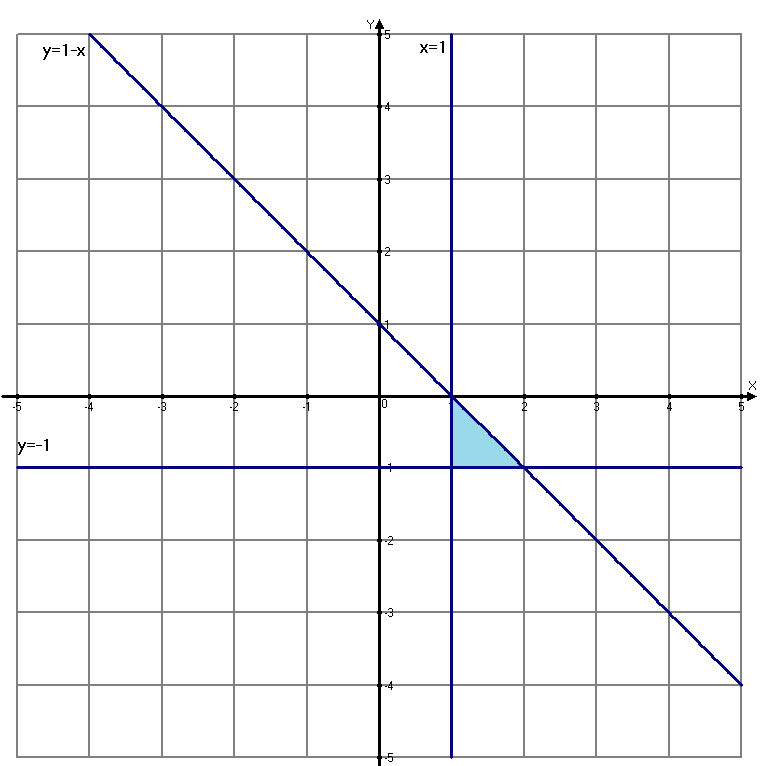 Находим стационарные точки 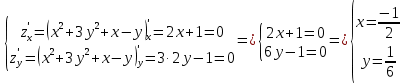 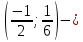 не принадлежит замкнутой области не принадлежит замкнутой областиИсследуем функцию на границе области 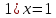 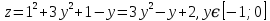 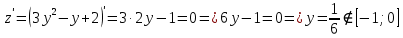 Добавим значения функции на конце отрезка 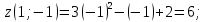 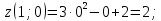 2) 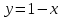 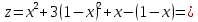 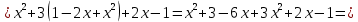 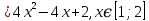 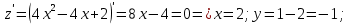 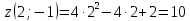 Добавим значения функции на конце отрезка 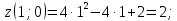 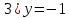 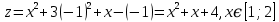 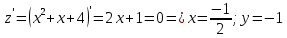 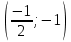 не принадлежит замкнутой области не принадлежит замкнутой областиДобавим значения функции на концах отрезка 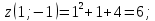 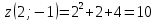 Сравнивая все полученные значения, получим наибольшее значение 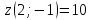 и наименьшее значение и наименьшее значение 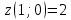 Ответ: наибольшее значение 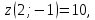 наименьшее значение наименьшее значение 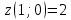 |