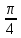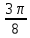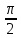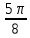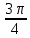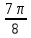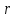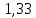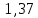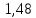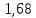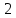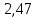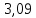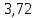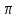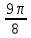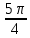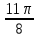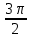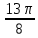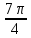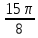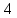Математика. КР. Контрольная работа 1 Вариант 6 Решить систему линейных алгебраических уравнений тремя способами
 Скачать 341.39 Kb. Скачать 341.39 Kb.
|
|
Контрольная работа № 1 Вариант № 6 6. Решить систему линейных алгебраических уравнений тремя способами: 1) по формулам Крамера; 2) методом Гаусса; 3) средствами матричного исчисления 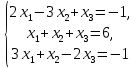 Решение: по формулам Крамера Составим определитель системы из коэффициентов при неизвестных и посчитаем его по правилу треугольника 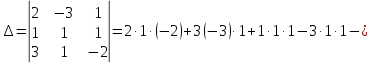 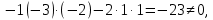 следовательно, система совместна и имеет единственное решение Найдем вспомогательные определители 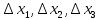 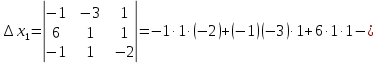 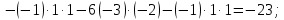 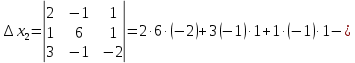 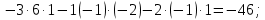 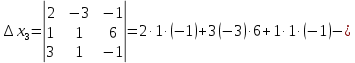 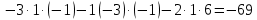 По формулам Крамера 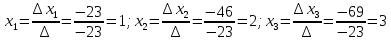 методом Гаусса Запишем расширенную матрицу системы 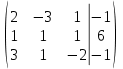 Поменяем местами первую и третью строки 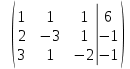 Умножим первую строку на 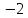 и сложим со второй строкой и сложим со второй строкойУмножим первую строку на 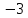 и сложим с третьей строкой и сложим с третьей строкой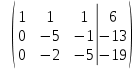 Умножим вторую строку на 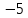 и сложим с третьей строкой и сложим с третьей строкой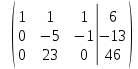 Разделим третью строку на 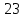 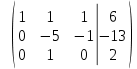 Расширенной матрице соответствует следующая система уравнений 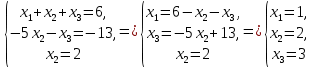 3) средствами матричного исчисления Решим систему матричным способом по формуле 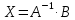 , ,где 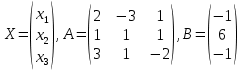 Найдем обратную матрицу 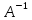 по формуле по формуле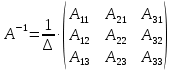 Для этого вычислим алгебраические дополнения 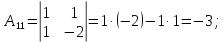 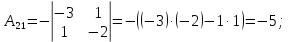 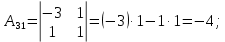 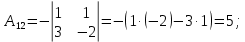 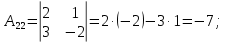 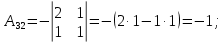 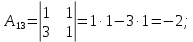 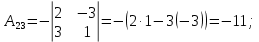 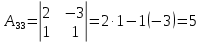 Таким образом, 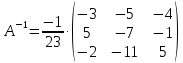 Отсюда искомая матрица 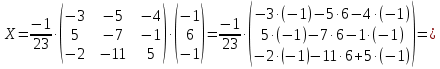 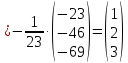 Ответ: 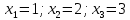 16. Даны координаты вершин пирамиды 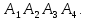 Требуется: Требуется:сделать чертеж; найти длину ребра 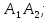 составить уравнение прямой 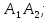 составить уравнение плоскости 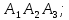 найти площадь грани 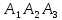 с использованием векторного произведения двух векторов; с использованием векторного произведения двух векторов;найти длину высоты, опущенной из вершины 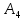 на грань на грань 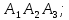 найти объем пирамиды с использованием смешанного произведения векторов; найти угол между ребрами 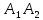 и и 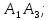 найти угол между ребром 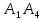 и гранью и гранью 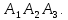 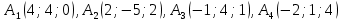 Решение: сделать чертеж 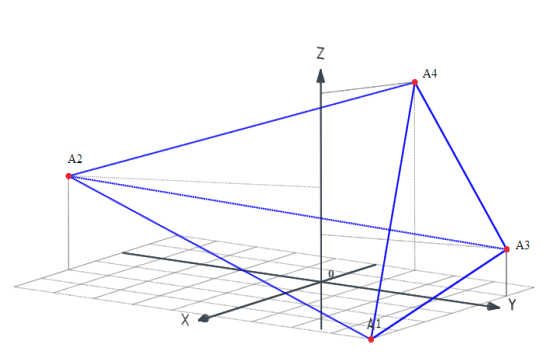 найти длину ребра 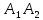 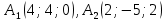 Найдем по формуле 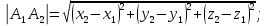 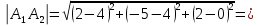 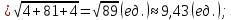 составить уравнение прямой 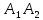 Уравнение прямой 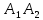 составим по точке составим по точке 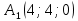 и направляющему вектору и направляющему вектору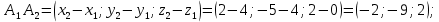 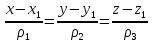 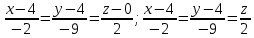 составить уравнение плоскости 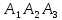 Найдем уравнение плоскости 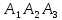 по формуле по формуле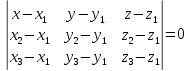 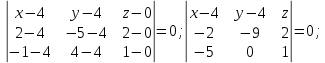 Приведем уравнение плоскости к общему виду 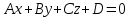 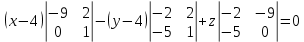 Раскроем определители 2-го порядка 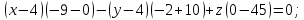 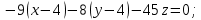 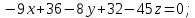 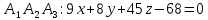 найти площадь грани 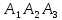 с использованием векторного произведения двух векторов с использованием векторного произведения двух векторов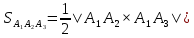 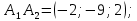 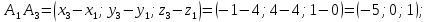 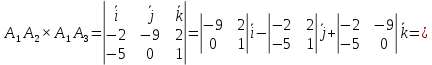 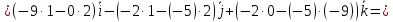 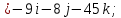 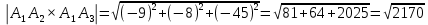 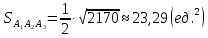 найти длину высоты, опущенной из вершины 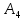 на грань на грань 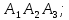 Длину высоты 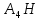 найдем как расстояние от точки найдем как расстояние от точки 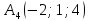 до плоскости до плоскости 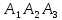 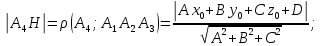 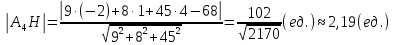 найти объем пирамиды с использованием смешанного произведения векторов 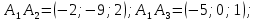 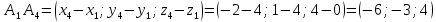 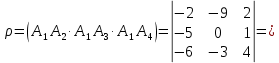 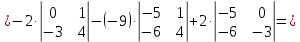 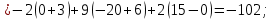 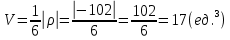 найти угол между ребрами 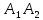 и и 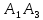 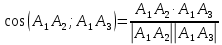 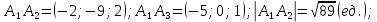 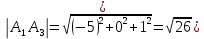 ед.) ед.)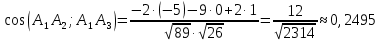 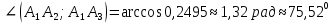 найти угол между ребром 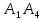 и гранью и гранью 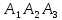 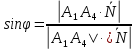 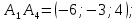 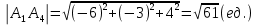 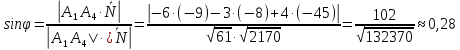 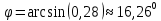 Ответ: 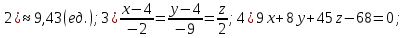 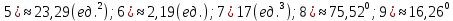 26. Составить уравнение гиперболы с фокусами на оси абсцисс, если длина его действительной оси равна 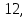 а эксцентриситет равен а эксцентриситет равен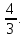 Решение: Каноническое уравнение гиперболы имеет вид 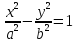 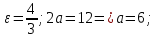 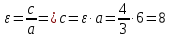 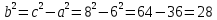 Тогда уравнение гиперболы 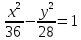  Ответ: Ответ: 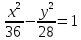 36. Линия задана уравнением 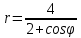 в полярной системе координат. в полярной системе координат. Требуется:1) построить линию по точкам, начиная от 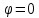 до до 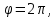 придавая 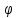 значения через промежуток значения через промежуток 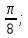 2) найти уравнение линии в прямоугольной декартовой системе координат, определить какая это линия. Решение: 1) построить линию по точкам, начиная от 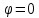 до до 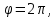 придавая 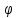 значения через промежуток значения через промежуток 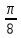 Составим таблицу значений функции
найти уравнение линии в прямоугольной декартовой системе координат, определить какая это линия. 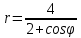 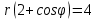 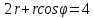 Используем формулы 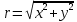 , , 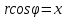 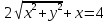 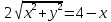 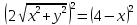 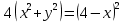 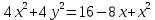 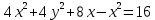 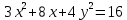 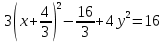 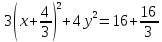 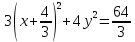 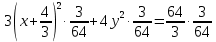 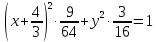 Тогда уравнение линии в прямоугольной декартовой системе координат 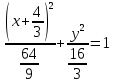 или 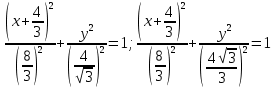 Данная кривая представляет собой эллипс с центром симметрии в точке 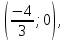 большой полуосью 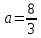 и малой полуосью и малой полуосью 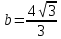 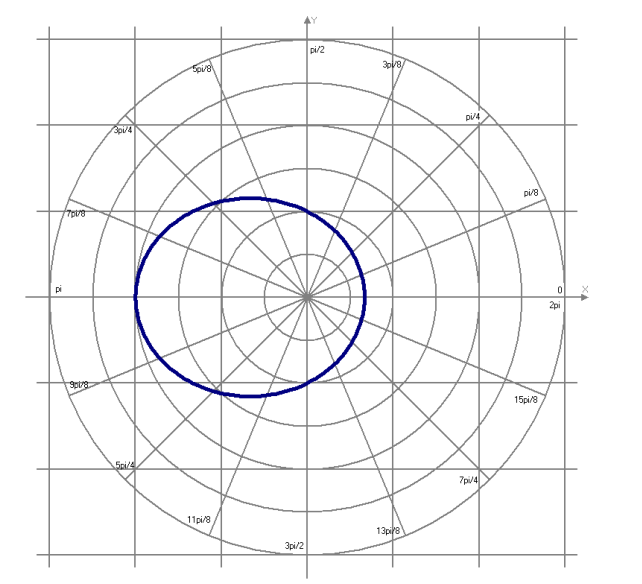 Ответ: 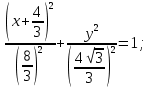 эллипс эллипс |