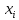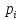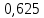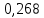Математика. КР. Контрольная работа 1 Вариант 6 Решить систему линейных алгебраических уравнений тремя способами
 Скачать 341.39 Kb. Скачать 341.39 Kb.
|
|
116. Вычислить интегралы 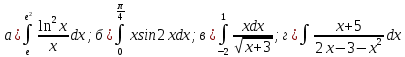 Решение: 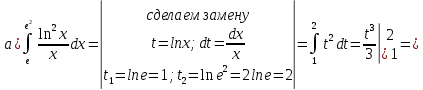 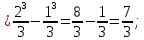 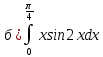 Применим формулу интегрирования по частям 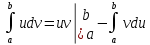 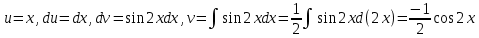 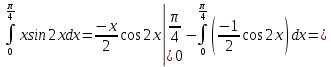 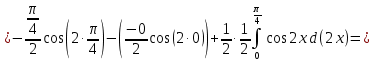 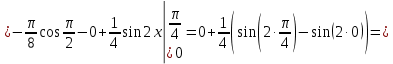 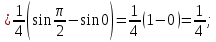 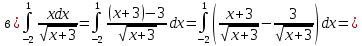 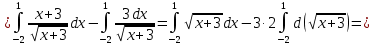 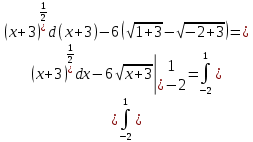 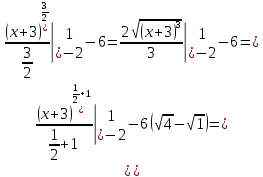 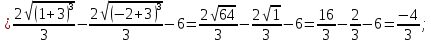 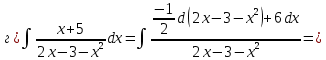 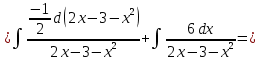 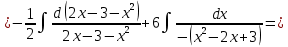 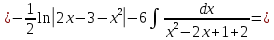 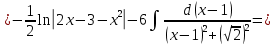 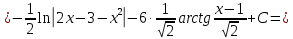 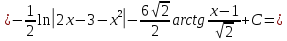 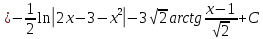 Ответ: 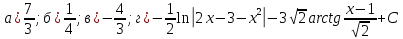 Контрольная работа № 2 Вариант № 6 126. Вычислить площадь фигуры, ограниченной линиями 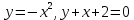 Решение: Построим графики этих функций 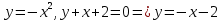 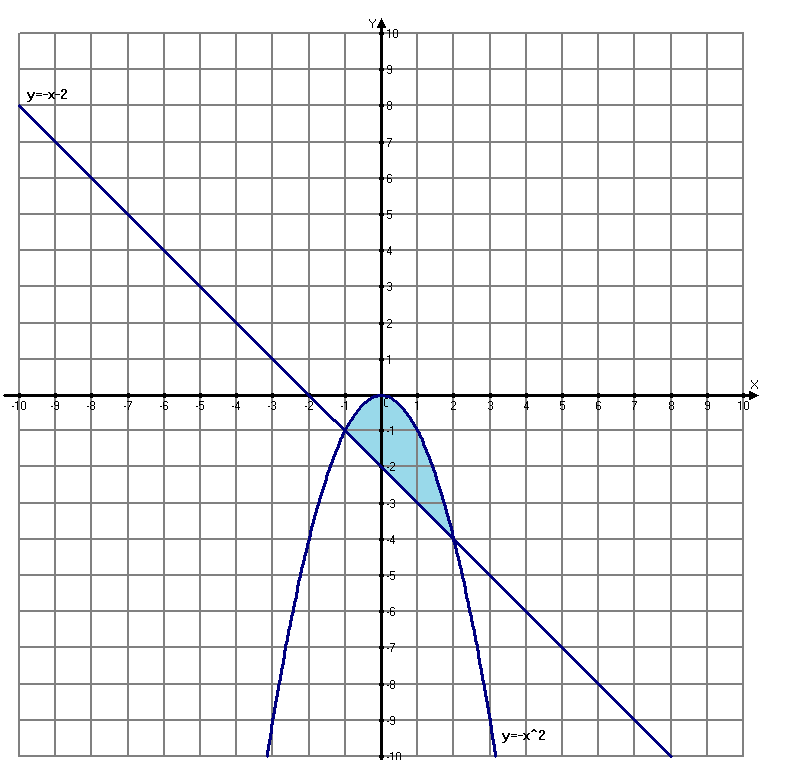 Найдем абсциссы точек пересечения графиков данных функций. Для этого решим систему 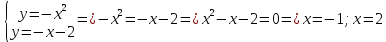 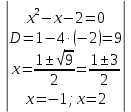 Искомую площадь найдем по формуле 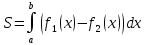 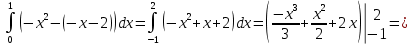 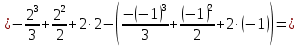 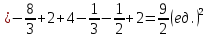 Ответ: 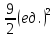 136. Решить дифференциальные уравнения 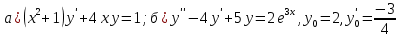 Решение: 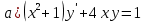 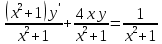 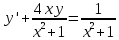 Это линейное дифференциальное уравнение первого порядка Проведем замену 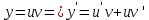 и подставим в уравнение и подставим в уравнение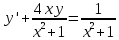 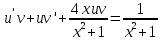 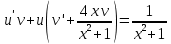 Составим и решим систему 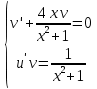 Из первого уравнения найдем 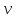 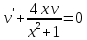 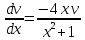 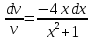 Интегрируем 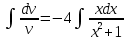 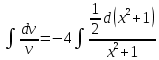 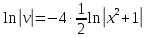 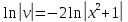 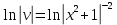 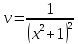 Подставим найденную функцию во второе уравнение системы и найдем функцию 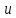 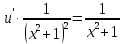 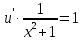 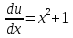 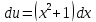 Интегрируем 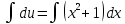 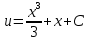 Таким образом, общее решение 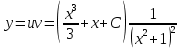 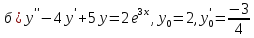 Найдем общее решение соответствующего однородного уравнения 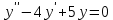 Составим и решим характеристическое уравнение: 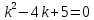 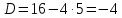 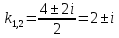 Получены сопряженные комплексные корни, поэтому общее решение: 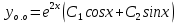 Частное решение неоднородного уравнения ищем в виде: 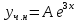 Найдем производные: 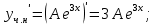 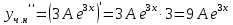 Подставим 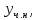 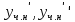 в левую часть неоднородного уравнения в левую часть неоднородного уравнения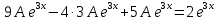 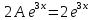 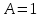 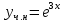 Общее решение неоднородного уравнения имеет вид 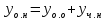 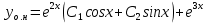 Найдем частное решение, соответствующее заданным начальным условиям: 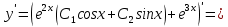 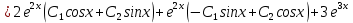 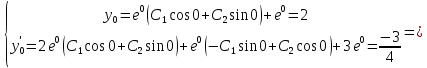 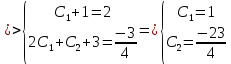 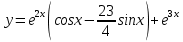 Ответ: 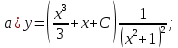 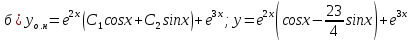 146. Найти три первых отличных от нуля члена разложения в степенной ряд решения 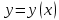 дифференциального уравнения дифференциального уравнения 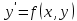 удовлетворяющему начальному условию удовлетворяющему начальному условию 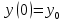 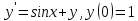 Решение: 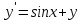 Разложение частного решения 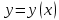 дифференциального уравнения при начальном условии дифференциального уравнения при начальном условии 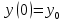 имеет вид: имеет вид: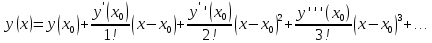 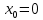 , следовательно, , следовательно, 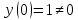 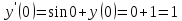 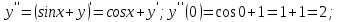 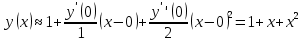 Ответ: 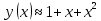 156. В урне 5 белых и 3 черных шара. Шары вынимают по одному до тех пор, пока не будет вынут белый шар. Составить закон распределения случайной величины 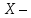 числа вынутых шаров. Найти: 1) функцию распределения числа вынутых шаров. Найти: 1) функцию распределения 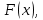 2) построить график функции 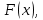 3) математическое ожидание 3) математическое ожидание 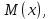 4) дисперсию 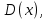 5) среднее квадратическое отклонение 5) среднее квадратическое отклонение 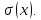 Решение: Рассмотрим все возможные значения, которые может принимать случайная величина X 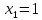 – первый вынутый шар окажется белым – первый вынутый шар окажется белым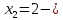 первый вынутый шар окажется черным, а второй белым первый вынутый шар окажется черным, а второй белым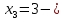 первых два шара окажутся черными, а третий белым первых два шара окажутся черными, а третий белым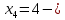 первые три шара будут черными, а четвертый белым первые три шара будут черными, а четвертый белымНайдем соответствующие им вероятности 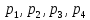 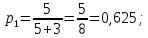 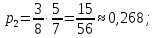 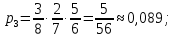 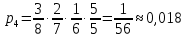 Тогда закон распределения дискретной случайной величины Х примет вид:
Проверим, что 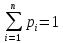 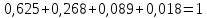 функция распределения 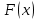 По определению функции распределения находим: 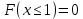 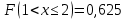 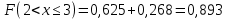 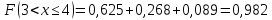 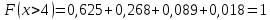 Таким образом, функция распределения 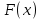 имеет вид: имеет вид: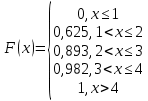 график функции 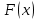 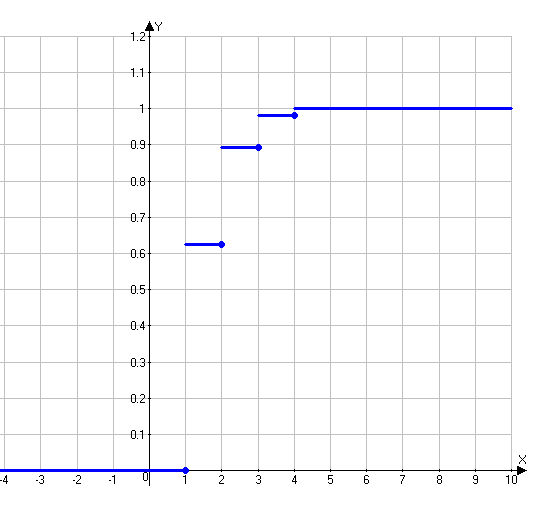 математическое ожидание 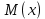 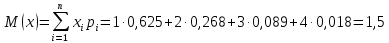 3) дисперсия D(x) D(x) 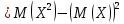 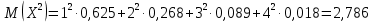 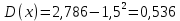 4) среднее квадратическое отклонение 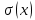 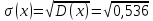 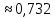 Ответ: 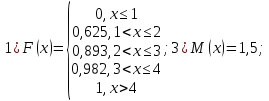 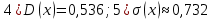 166. Случайная величина X задана интегральной функцией 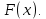 Требуется : Требуется :1) найти дифференциальную функцию 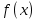 (плотность вероятности); 2) найти математическое ожидание и дисперсию; 3) построить графики интегральной и дифференциальной функций (плотность вероятности); 2) найти математическое ожидание и дисперсию; 3) построить графики интегральной и дифференциальной функций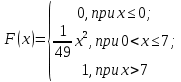 Решение: 1) найти дифференциальную функцию 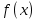 (плотность вероятности); (плотность вероятности);т.к. 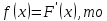 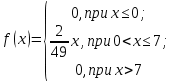 2) найти математическое ожидание и дисперсию 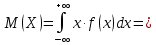 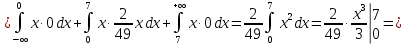 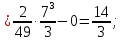 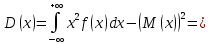 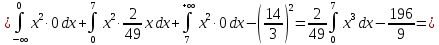 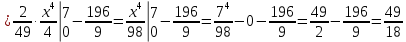 3) построить графики интегральной и дифференциальной функций Построим график интегральнойфункции 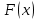 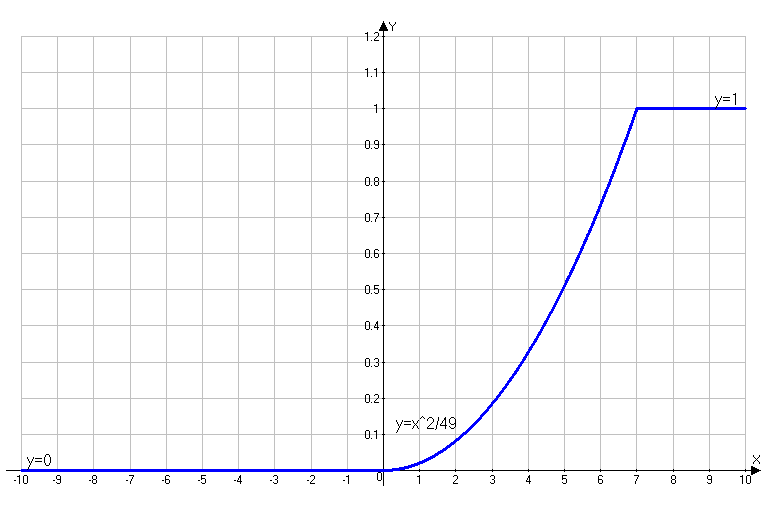 Построим график дифференциальной функции  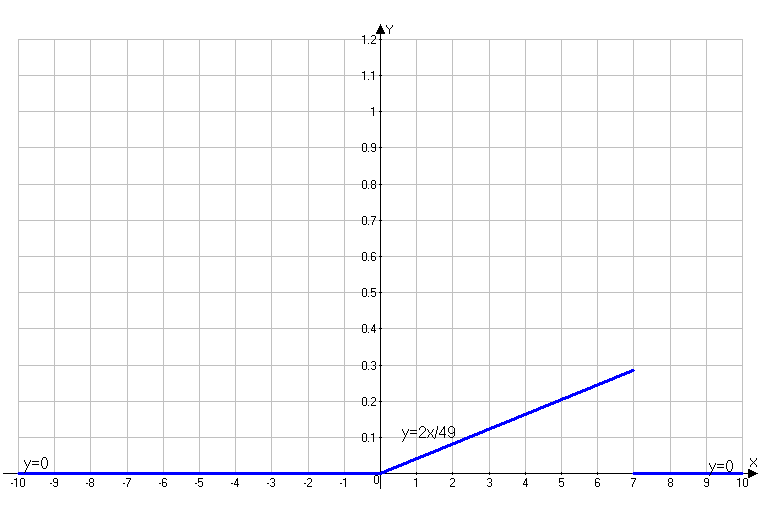 Ответ: 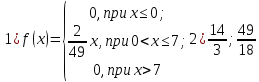 |