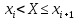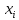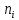КР_Теоряи вероятностей и матстатистика. 01_03_21_ТВиМС_КР. Контрольная работа Часть 1 теория вероятностей Задача 1
 Скачать 145.25 Kb. Скачать 145.25 Kb.
|
|
Контрольная работа Часть 1: теория вероятностей Задача №1 Партия из 110изделий содержит 22бракованных изделия. Какова вероятность того, что среди выбранных наудачу 10изделий ровно 5окажутся бракованными? Решение Применим классическую схему. Пусть А – событие, состоящее из выборок, содержащих 5бракованных изделия и 5качественных. Число элементарных событий, благоприятствующих событию А, равно 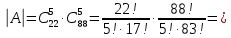 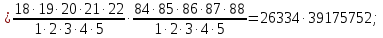 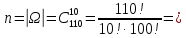 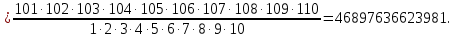 Таким образом, 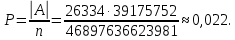 Задача №2 В первой урне 11белых и 12чёрных шаров, а во второй урне 6белых и 7чёрных шаров. Из первой урны случайным образом взяли 10шаров, а из второй – 5шаров. Найти вероятность, что среди извлечённых шаров; а) все шары одного цвета; б) хотя бы один белый шар. Решение Шары вынимали из обеих урн независимо. Испытаниями являются извлечение 10шаров из первой урны и 5шаров из второй. Элементарными событиями будут сочетания по 10шаров из 23 и по 5шаров из 13. Вычислим количество всех выборок из первой и второй урн, которые обозначим n1 и n2 соответственно: 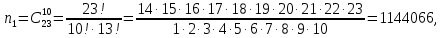 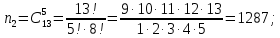 а) Пусть событие А – все вынутые шары одного цвета. Рассмотрим события: В1 – из первой урны извлекли 10белых шаров; В2 –из первой урны извлекли 10чёрных шаров; С1 – из второй урны извлекли 5белых шаров; С2 – из второй урны извлекли 5чёрных шаров. При этом событие А выражается через остальные следующим образом: А=В1·С1+В2·С2. Учитывая независимость и несовместность событий, а также следствие из второго свойства вероятности, получим: P(А)=P(В1) ·P(С1) +P(В2) ·P(С2). Вычислим количество элементарных событий, благоприятствующих наступлению каждого события, вошедшего в полученную формулу: 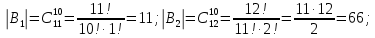 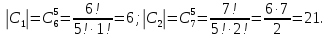 Следовательно, 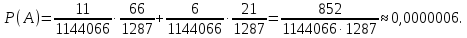 Задача №3 Устройство состоит из трёх независимо функционирующих элементов, работающих в течение времени Т безотказно соответственно с вероятностями 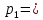 0,87, 0,87, 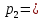 0,65, 0,65, 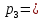 0,92. Найти вероятность того, что за время Т выйдет из строя ровно два элемента. 0,92. Найти вероятность того, что за время Т выйдет из строя ровно два элемента.Решение Пусть событие А – за время Т вышло из строя ровно два элемента. Рассмотрим события Аi (i=1,2,3), состоящие в том, что за это время i–й элемент вышел из строя. Тогда противоположные им события Аi заключаются в том, что i–й элемент не вышел из строя. Имеем: 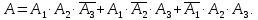 Учитывая независимость элементов устройства и несовместность событий 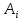 и и 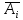 , а также свойства вероятности, получаем следующую формулу: , а также свойства вероятности, получаем следующую формулу: 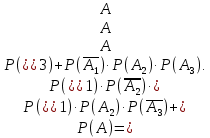 Нам даны вероятности безотказной работы элементов, то есть событий 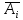 . Воспользуемся первым свойством вероятности: . Воспользуемся первым свойством вероятности: 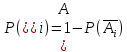 , , 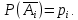 Итак получим: 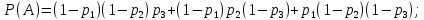 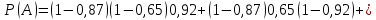 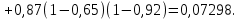 Задача №4 В одной урне 11белых и 12чёрных шаров, а в другой – 6белых и 7 чёрных шаров. Из первой урны случайным образом вынимают два шара и опускают во вторую урну. После этого из второй урны также случайно вынимают три шара. Найти вероятность, что все шары, вынутые из второй урны, окажутся белые. Решение В этой задаче испытания происходят в два этапа: в начале случайным образом вынимают шары из первой урны и опускают во вторую, а затем случайно вынимают шары из второй урны. Рассмотрим события: А – из второй урны вынули три белых шара; Н1 – из первой урны взяли два белых шара; Н2 – из первой урны взяли 1 белый и 1 чёрный шар; Н3 – из первой урны взяли два чёрных шара. Совокупность событий {Н1, Н2, Н3} является полной группой гипотез. Используя формулу полной вероятности, получим: 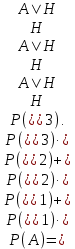 Общее число выборок из первой урны равно 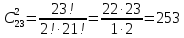 , а из второй - , а из второй - 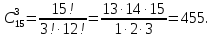 Вычислим количество элементарных событий, благоприятствующих наступлению гипотез: 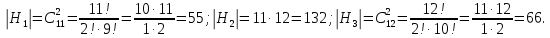 Если осуществилась гипотеза Н1, то во второй урне оказалось 8 белых шаров. Поэтому 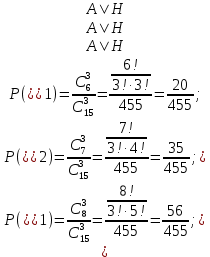 Таким образом, имеем: 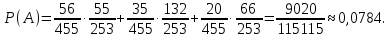 Задача №5 В пирамиде стоят 110винтовок, из них 10с оптическим прицелом. Стрелок, стреляя из винтовки с оптическим прицелом, может поразить мишень с вероятностью p1=0,87 а стреляя из винтовки без оптического прицела, – с вероятностью p2=0,65. Стрелок поразил мишень. Найти вероятность того, что при этом он стрелял из винтовки с оптическим прицелом. Решение В этой задаче первым испытанием является случайный выбор винтовки, вторым – стрельба по мишени. Рассмотрим следующие события: А – стрелок поразил мишень; Н1 – стрелок взял винтовку с оптическим прицелом; Н2 – стрелок взял винтовку без оптического прицела. Как следует из условия задачи, событие А уже осуществилось, то есть стрелок попал в мишень. Найти же нужно вероятность того, что при этом он стрелял из винтовки с оптическим прицелом, то есть условную вероятность 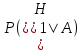 . Используем формулу Байеса. Имеем: . Используем формулу Байеса. Имеем: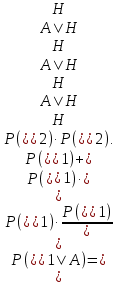 Используя классическое определение вероятности и учитывая, что выбирается одна винтовка, найдём вероятности гипотез Н1 и Н2. Получим: 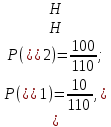 Условные вероятности, входящие в формулу, заданы в условии задачи. Следовательно: 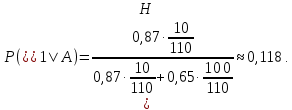 Задача №6 Игральная кость бросается 10раз. Найти вероятность, что при этом шестёрка выпала ровно 5раз. Решение При каждом бросании будем считать успехом выпадение шестёрки, а неудачей – выпадение любого другого числа. Тогда мы попадаем в рамки схемы Бернулли с 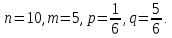 Получаем: 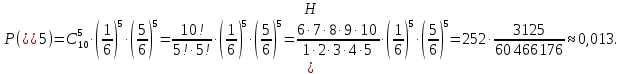 Задача №7 На телефонной станции неправильное соединение происходит с вероятностью 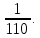 Найти вероятность, что среди 550 соединений произойдёт: Найти вероятность, что среди 550 соединений произойдёт: а) точно одно неправильное соединение; б) больше, чем два неправильных соединения. Решение Так как вероятность события мала, а количество испытаний велико, можно использовать формулу Пуассона. Здесь 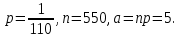 а) Применяя формулу Пуассона, получим: 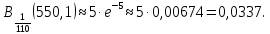 б) Искомая вероятность равна: 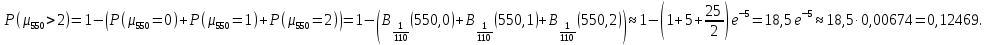 Задача №8 Случайная величина Х задана законом распределения:
Найти р, функцию распределения F(x) с.в. Х, построить её график. Вычислить для с.в. Х математическое ожидание МХ и дисперсию DX. Решение Из определения закона распределения известно, что сумма чисел в нижнем ряду таблицы должна равняться единице. Исходя из этого, найдём неизвестный параметр р: p=1-0,2-0,4=0,4. Для того,чтобы найти функцию распределения, воспользуемся формулой из определения функции распределения. Получим: 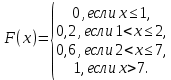 График функции 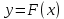 имеет вид: имеет вид: 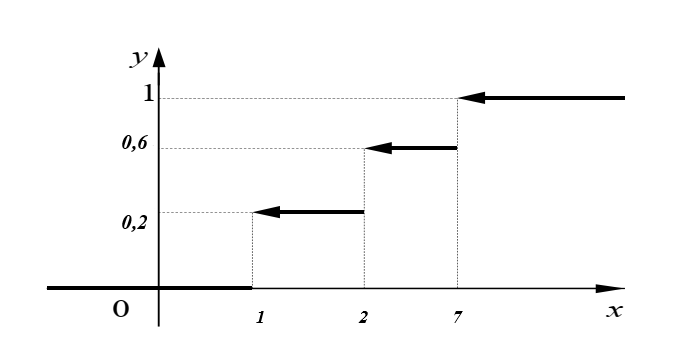 Найдём математическое ожидание: 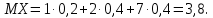 Найдём дисперсию: 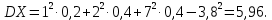 Задача №9 Случайная величина Х задана следующей плотностью распределения: 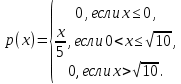 Найти функцию распределения 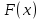 с.в. Х, построить графики функций с.в. Х, построить графики функций 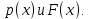 Вычислить для с.в. Х её математическое ожидание МХ и дисперсию DX. Вычислить для с.в. Х её математическое ожидание МХ и дисперсию DX.Решение Функцию распределения непрерывной случайной величины найдём по формуле (44), воспользовавшись также свойствами функции распределения. Отдельно вычислим функцию распределения на интервале 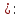 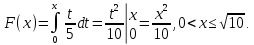 Таким образом, на всей области определения имеем: 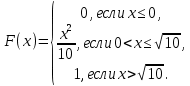 Построим графики заданной плотности распределения с.в. Х и найденной функции распределения. (Требуется выполнить точные построения согласно данным варианта!) График плотности 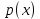 имеет вид: имеет вид: 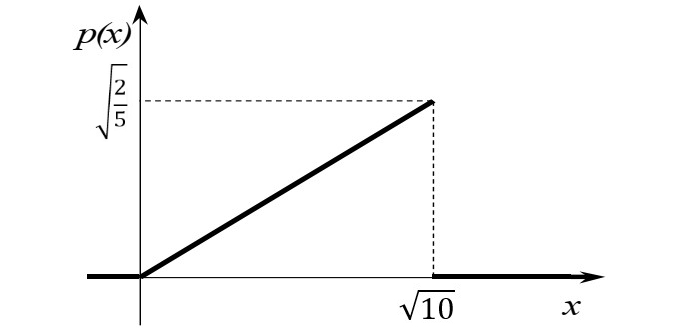 График функции распределения 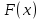 : : 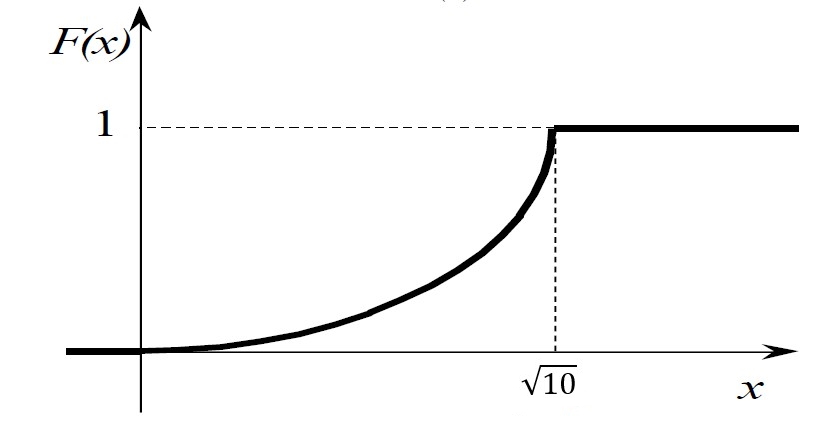 Математическое ожидание вычислим по формуле: 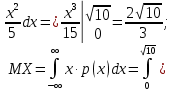 Дисперсию вычислим по формуле: 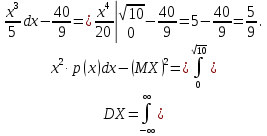 Задача №10 Случайная величина Х задана функцией распределения: 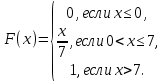 Найти плотность распределения 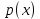 с.в. Х, построить графики функций с.в. Х, построить графики функций 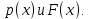 Вычислить для с.в. Х её математическое ожидание МХ и дисперсию DX. Вычислить для с.в. Х её математическое ожидание МХ и дисперсию DX.Решение. Плотность распределения 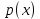 с.в. Х: с.в. Х: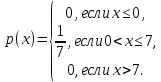 График плотности 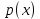 имеет вид: имеет вид: 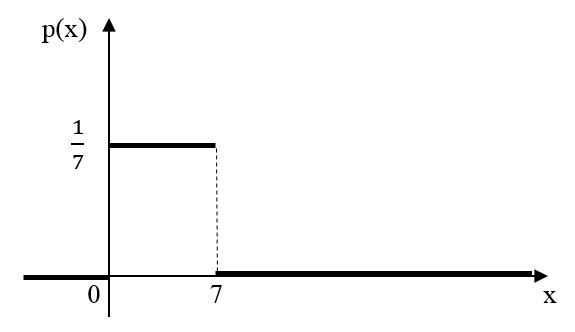 График функции распределения 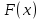 : : 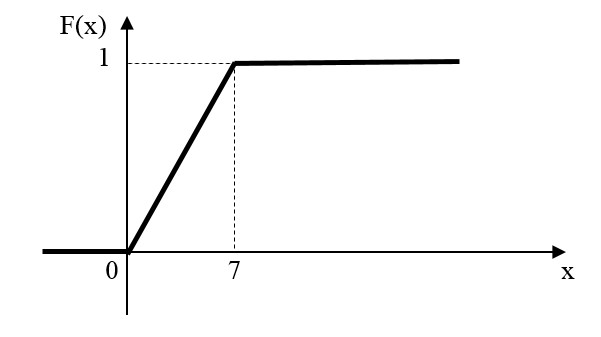 Математическое ожидание вычислим по формуле: 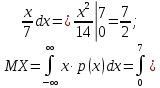 Дисперсию вычислим по формуле: 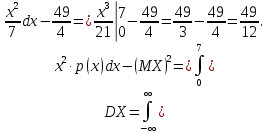 Часть 2: математическая статистика Задача 1 В результате проведения исследований получены следующие статистические данные
где 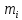 – частота попадания вариант в промежуток – частота попадания вариант в промежуток 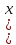 . Для выборки построить гистограмму относительных частот. . Для выборки построить гистограмму относительных частот. Решение. Объём выборки n=50. Найдём относительные частоты: 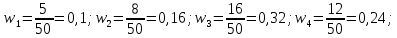 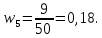 Найдём плотности относительных частот, учитывая, что длина интервала h=2: 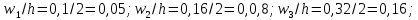 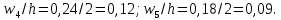 Построим на оси абсцисс данные частичные интервалы. Проведем над этими интервалами отрезки, параллельные оси абсцисс и находящиеся от неё на расстояниях, равных соответствующим плотностям относительной частоты. Например, над интервалом (2,4) проведем отрезок, параллельный оси абсцисс и находящийся от неё на расстоянии, равном 0,05; аналогично строят остальные отрезки. Искомая гистограмма относительных частот изображена на рисунке ниже. 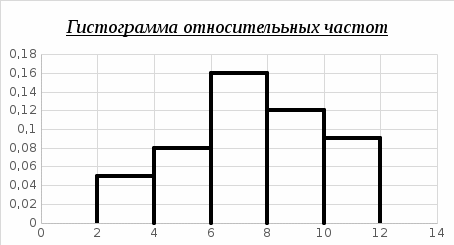 Задача 2 В ходе эксперимента получены данные наблюдений:
Для данной выборки выполнить следующее: Вычислить числовые характеристики выборки (мода, медиана, выборочное среднее, выборочная дисперсия, среднее квадратическое отклонение, начальные и центральные моменты); Найти несмещенные оценки генерального среднего и генеральной дисперсии. Решение. Найдем числовые характеристики данной выборки: Минимальное и максимальное значение выборки:  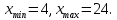 Размах выборки: 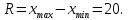 Мода: 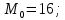 Так как вариационный ряд содержит четное число вариант (n=100), то медиана 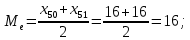 Выборочное среднее: 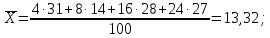 Выборочная дисперсия: 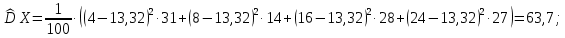 Среднее квадратическое отклонение: Начальные моменты: 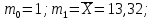 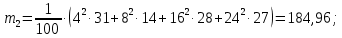 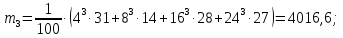 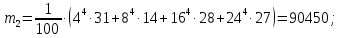 Центральные моменты: 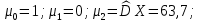 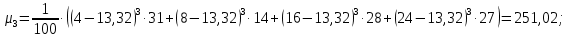 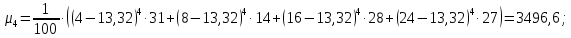 Несмещенной оценкой генерального среднего является выборочное среднее: 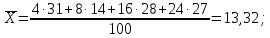 Несмещенной оценкой генеральной дисперсии является исправленная выборочная дисперсия: 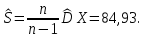 Задача 3 Найти доверительный интервал для неизвестного математического ожидания а случайной величины Х, распределенной нормально, если известны объем выборки n=25, выборочное среднее 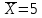 , надежность , надежность 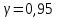 и среднее квадратическое отклонение и среднее квадратическое отклонение 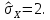 Решение. Построим доверительный интервал для математического ожидания при неизвестном параметре 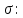 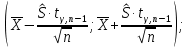 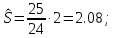 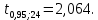 Тогда получим интервал, покрывающий а с надежностью 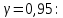 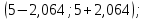 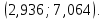 Задача 4 Генеральная совокупность имеет нормальное распределение, для которого известно значение параметра 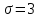 . Найти наименьший объем выборки, при . Найти наименьший объем выборки, прикотором доверительный интервал длиной 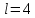 покрывает параметр а с покрывает параметр а снадежностью =0,9. Решение. Доверительный интервал для математического ожидания при известном Параметре 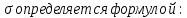 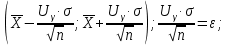 По условию 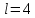 , следовательно, , следовательно, 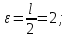 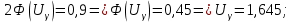 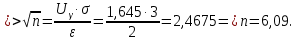 Следовательно, наименьшим объемом выборки будет 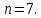 Задача 5 Найти доверительный интервал для неизвестного среднего квадратического отклонения нормально распределенной случайной величины Х, если известны объем выборки n=50, надежность 0,95 и выборочная дисперсия 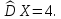 Решение. Доверительный интервал для неизвестного среднего квадратического отклонения определяется формулой: 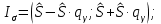 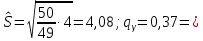 Следовательно, интервал 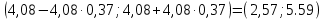 является доверительным для параметра с надежностью 0,95. |