Вопросы. вопросы. 1. Вероятность. Вероятностное пространство. Свойства
 Скачать 6.39 Mb. Скачать 6.39 Mb.
|
№1.Вероятность. Вероятностное пространство. Свойства.1) Вероятностью P(A) события A называется отношение числа элементарных событий m, благоприятствующих событию A, к числу всех элементарных событий n. Вероятностным пространством наз-ся тройка (Ώ, А, P), где Ώ - произвольное мн-во, А - алгебра подмножеств пространства Ώ, P - вещественная функция, заданная на А. Св-ва: 1) 2) 3) если №2.Формула Байеса. Формула полной вероятности.Вероятность гипотез. Формулы Байеса Пусть событие A может наступить при условии появления одного из несовместных событий , образующих полную группу. Поскольку заранее не известно, какое из этих событий наступит, их называют гипотезами. Вероятность появления события A определяется по формуле полной вероятности: Допустим, что произведено испытание, в результате которого появилось событие А. Поставим своей задачей определить, как изменились (в связи с тем, что событие А уже наступило) вероятности гипотез. Другими словами, будем искать условные вероятности Найдем сначала условную вероятность . ПО теореме умножения имеем Отсюда Заменив здесь Р (А) по формуле (*), получим Аналогично выводятся формулы, определяющие условные вероятности остальных гипотез, т. е. условная вероятность любой гипотезы может быть вычислена по формуле Полученные формулы называют формулами Байеса (по имени английского математика, который их вывел; опубликованы в 1764 г.). Формулы Бейеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А. Формула полной вероятности Теорема. Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий B1,B2…Bn, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А: Эту формулу называют «формулой полной вероятности». Доказательство. По условию, событие А может наступить, если наступит одно из несовместных событий B1,B2…Bn. Другими словами, появление события А означает осуществление одного, безразлично какого, из несовместных событий B1A,B2A…BnA. Пользуясь для вычисления вероятности события А теоремой сложения, получим Остается вычислить каждое из слагаемых. По теореме умножения вероятностей зависимых событий имеем 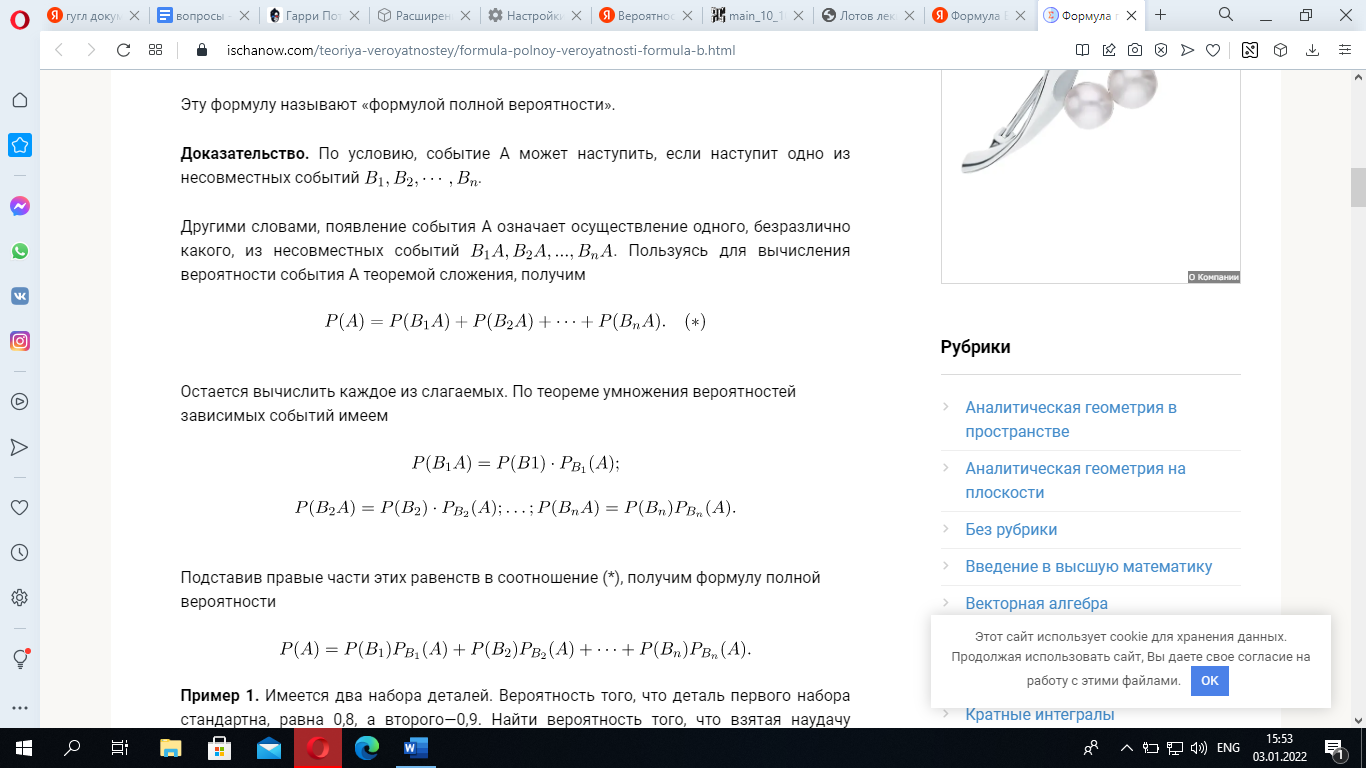 Подставив правые части этих равенств в соотношение (*), получим формулу полной вероятности Формула Байеса: P(A | B) = P(B | A) * P(A) \ P(B), где P(A) - априорная вероятность гипотезы A, P(A | B) - вероятность гипотезы A при наступлении события B , P(B | A) - вероятность наступления события B при истинности гипотезы A, P(B) - полная вероятность наступления события B. №3.Биномиальное и пуассоновское распределения.Биномиальное распределениеПусть имеется некое событие A. Вероятность появления события A равна p, вероятность непоявления события A равна 1 – p, иногда ее обозначают как q. Пусть n — число испытаний, m — частота появления события A в этих n испытаниях. Известно, что суммарная вероятность всех возможных комбинаций исходов равна единице, то есть:  Математическое ожидание M биномиального распределения равно:  Пример 1. Вычислить вероятность того, что событие, имеющее вероятность p = 0.5, в n = 10 испытаниях произойдет m = 1 раз. Имеем: C101 = 10, и далее: P1 = 10 · 0.51 · (1 – 0.5)10 – 1 = 10 · 0.510 = 0.0098. Как видим, вероятность наступления этого события достаточно мала. Объясняется это, во-первых, тем, что абсолютно не ясно, произойдет ли событие или нет, поскольку вероятность равна 0.5 и шансы здесь «50 на 50»; а во-вторых, требуется исчислить то, что событие произойдет именно один раз (не больше и не меньше) из десяти. Пример 2. Вычислить вероятность того, что событие, имеющее вероятность p = 0.5, в n = 10 испытаниях произойдет m = 2 раза. Имеем: C102 = 45, и далее: P2 = 45 · 0.52 · (1 – 0.5)10 – 2 = 45 · 0.510 = 0.044. Вероятность наступления этого события стала больше! |
