Вопросы. вопросы. 1. Вероятность. Вероятностное пространство. Свойства
 Скачать 6.39 Mb.
|
№13. Центральная предельная теорема для разнораспределенных слагаемых. (Теорема Линдеберга-Феллера.)В "Основы вероятностно-статистических методов описания неопределенностей" уже был приведен простейший вариант центральной предельной теоремы (ЦПТ) теории вероятностей. Центральная предельная теорема (для одинаково распределенных слагаемых). Пусть 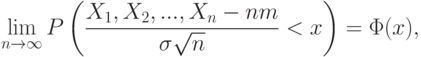 . - независимые одинаково распределенные случайные величины с математическими ожиданиями  и дисперсиями  .. Тогда для любого действительного числа  существует предел где  - функция стандартного нормального распределения.Эту теорему иногда называют теоремой Линдеберга-Леви [  , с.122].В ряде прикладных задач не выполнено условие одинаковой распределенности. В таких случаях центральная предельная теорема обычно остается справедливой, однако на последовательность случайных величин приходится накладывать те или иные условия. Суть этих условий состоит в том, что ни одно слагаемое не должно быть доминирующим, вклад каждого слагаемого в среднее арифметическое должен быть пренебрежимо мал по сравнению с итоговой суммой. Наиболее часто используется теорема Ляпунова. Центральная предельная теорема (для разнораспределенных слагаемых) - теорема Ляпунова. Пусть 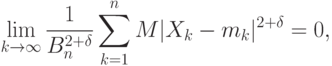. - независимые случайные величины с математическими ожиданиями  и дисперсиями  .. Пусть при некотором  у всех рассматриваемых случайных величин существуют центральные моменты порядка  и безгранично убывает "дробь Ляпунова": где 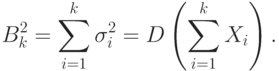 Тогда для любого действительного числа существует предел
где - функция стандартного нормального распределения.В случае одинаково распределенных случайных слагаемых  и теорема Ляпунова переходит в теорему Линдеберга-Леви. История получения центральных предельных теорем для случайных величин растянулась на два века - от первых работ Муавра в 30-х годах XVIII в. до необходимых и достаточных условий, полученных Линдебергом и Феллером в 30-х годах XX в. Теорема Линдеберга-Феллера. Пусть 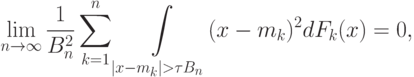. - независимые случайные величины с математическими ожиданиями и дисперсиями  . Предельное соотношение (1), т.е. центральная предельная теорема, выполнено тогда и только тогда, когда при любом   где  обозначает функцию распределения случайной величины  .Доказательства перечисленных в настоящем подразделе центральных предельных теорем для случайных величин можно найти в классическом курсе теории вероятностей [ [ 2.3 ] ]. Для прикладной статистики большое значение имеет многомерная центральная предельная теорема. В ней речь идет не о сумме случайных величин, а о сумме случайных векторов. Необходимое и достаточное условие многомерной сходимости [ [ 4.23 ] , с.124]. Пусть  обозначает совместную функцию распределения  -мерного случайного вектора  ., и  - функция распределения линейной комбинации  . Необходимое и достаточное условие для сходимости к некоторой -мерной функции распределения  состоит в том, что имеет предел для любого вектора  .Приведенная теорема ценна тем, что сходимость векторов сводитcя к сходимости линейных комбинаций их координат, т.е. к сходимости обычных случайных величин, рассмотренных ранее. Однако она не дает возможности непосредственно указать предельное распределение. Это можно сделать с помощью следующей теоремы. Теорема о многомерной сходимости. Пусть и - те же, что в предыдущей теореме. Пусть - совместная функция распределения -мерного случайного вектора  . Если функция распределения сходится при росте объема выборки к функции распределения  для любого вектора  , где - функция распределения линейной комбинации  , то сходится к .Здесь сходимость к означает, что для любого -мерного вектора  такого, что функция распределения непрерывна в , числовая последовательность  сходится при росте  к числу  . Другими словами, сходимость функций распределения понимается ровно также, как при обсуждении предельных теорем для случайных величин выше. Приведем многомерный аналог этих теорем.Многомерная центральная предельная теорема [ [ 4.23 ] ]. Рассмотрим независимые одинаково распределенные -мерные случайные векторы где штрих обозначает операцию транспонирования вектора. Предположим, что случайные векторы 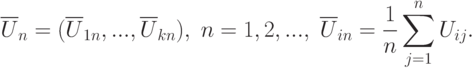 имеют моменты первого и второго порядка, т.е. где  - вектор математических ожиданий координат случайного вектора,  - его ковариационная матрица. Введем последовательность средних арифметических случайных векторов: Тогда случайный вектор  имеет асимптотическое -мерное нормальное распределение  , т.е. он асимптотически распределен так же, как -мерная нормальная величина с нулевым математическим ожиданием, ковариационной и плотностью Здесь  - определитель матрицы . Другими словами, распределение случайного вектора сходится к -мерному нормальному распределению с нулевым математическим ожиданием и ковариационной матрицей .Напомним, что многомерным нормальным распределением с математическим ожиданием и ковариационной матрицей называется распределение, имеющее плотность Многомерная центральная предельная теорема показывает, что распределения сумм независимых одинаково распределенных случайных векторов при большом числе слагаемых хорошо приближаются с помощью нормальных распределений, имеющих такие же первые два момента (вектор математических ожиданий координат случайного вектора и его корреляционную матрицу), как и исходные векторы. От одинаковой распределенности можно отказаться, но это потребует некоторого усложнения символики. В целом из теоремы о многомерной сходимости вытекает, что многомерный случай ничем принципиально не отличается от одномерного. Пример. Пусть  .- независимые одинаково распределенные случайные величины. Рассмотрим -мерные независимые одинаково распределенные случайные векторы Их математическое ожидание - вектор теоретических начальных моментов, а ковариационная матрица составлена из соответствующих центральных моментов. Тогда  - вектор выборочных начальных моментов. Многомерная центральная предельная теорема утверждает, что имеет асимптотически нормальное распределение. Как вытекает из теорем о наследовании сходимости и о линеаризации (см. ниже), из распределения можно вывести распределения различных функций от выборочных начальных моментов. А поскольку центральные моменты выражаются через начальные, то аналогичное утверждение верно и для них. |
