|
|
Вопросы. вопросы. 1. Вероятность. Вероятностное пространство. Свойства
№9.Формулы обращения для характеристических функций.



№10. Математическое ожидание. Свойства. Дисперсия.

Cвойства математического ожидания:
Математическое ожидание имеет ту же размерность, что и сама случайная величина.
Математическое ожидание может быть как положительным, так и отрицательным числом.
Математическое ожидание постоянной величины С равно этой постоянной. М (С) = С.
Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий этих величин.
M(X+Y+...+W)=M(X)+M(Y)+...+M(W).
Математическое ожидание произведения двух или нескольких взаимно независимых случайных величин равно произведению математических ожиданий этих величин. М(XY) = M(X) × M(Y).
Постоянный множитель можно выносить за знак математического ожидания: M(C×X)=C×M(X).

№11.Сходимость по вероятности. Законы больших чисел для сумм одинаково распределенных слагаемых. Сходимость по вероятности.
Понятие сходимости в теории вероятностей отличается от определения сходимости, принятого в математическом анализе. Напомним, что в математическом анализе последовательность {х„} сходится, если существует такое действительное число а, что для любого положительного е существует номер числовой последовательности п0, начиная с которого для всех членов последовательности справедливо неравенство |х„ - а а-еп
Последнее неравенство означает, что все члены последовательности попадают в е-окрестность числа а за исключением, возможно, конечного числа начальных точек. Рассмотрим последовательность (-1)" 1
х„ =1 н--Если взять е = —, то начиная с номера п0 - 3 справедливо
п 2
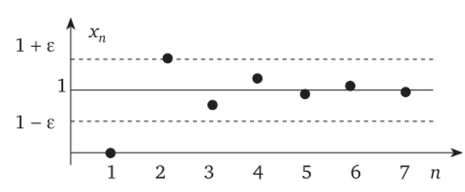
неравенство |х„ -1|<—. На рис. 9.1 построена эта последовательность.
Точками указаны члены последовательности, е-окрестность числа 1,
равная (1-е;1 + е) = —; — , выделена двумя пунктирными линиями, ука- 2 2)
зано число х3, начиная с которого все члены последовательности ока-
зываются внутри е-окрестности. Число 1 есть предел числовой последо- ( (-1)" ^
вательности: lim 1+- =1.
п-х»^ п )
В теории вероятностей говорят, что последовательность случайных величин {?„} сходится по вероятности (convergence in probability) к случайной величине если для любого положительного числа е вероятность события | ?„ - ? | < е стремится к единице при п —» со:
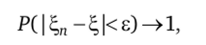
или, что эквивалентно,
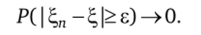
на всякий: https://studme.org/320836/matematika_himiya_fizik/shodimosti_teorii_veroyatnostey
Закон больших чисел в форме Чебышева для одинаково распределенных слагаемых.
Пусть  — независимые, одинаково распределенные случайные величины с — независимые, одинаково распределенные случайные величины с 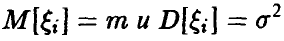 Тогда Тогда
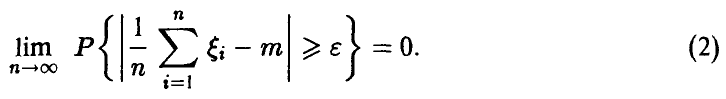
Замечание:
Условие существования дисперсий может быть опущено (закон больших чисел в форме Хинчина).
Другим важным следствием теоремы Чебышева является теорема Я. Бернулли.
Следствие:
Закон больших чисел в форме Бернулли.
Пусть — число успехов в серии из n независимых испытаний с постоянной вероятностью успеха р в каждом испытании и 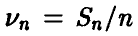 — относительная частота числа успехов. Тогда с увеличением количества экспериментов п в подавляющем большинстве случаев частота будет мало отличаться от вероятности. Точнее — относительная частота числа успехов. Тогда с увеличением количества экспериментов п в подавляющем большинстве случаев частота будет мало отличаться от вероятности. Точнее
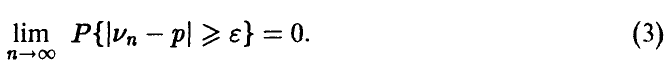
◄ Доказательство следует из (2), если взять 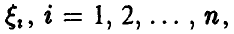 такие, что такие, что 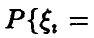 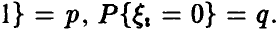 Тогда Тогда 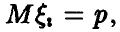 дисперсия величины существует, равна pq и применима теорема Чебышева, при этом дисперсия величины существует, равна pq и применима теорема Чебышева, при этом
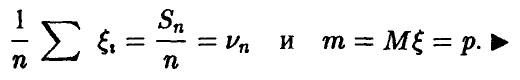
№12.Неравенство Чебышева.


|
|
|
 Скачать 6.39 Mb.
Скачать 6.39 Mb.
