Вопросы. вопросы. 1. Вероятность. Вероятностное пространство. Свойства
 Скачать 6.39 Mb. Скачать 6.39 Mb.
|
Распределение ПуассонаРаспределение Пуассона — это частный случай биномиального распределения (при n >> 0 и при p –> 0 (редкие события)). Из математики известна формула, позволяющая примерно подсчитать значение любого члена биномиального распределения: 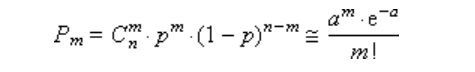  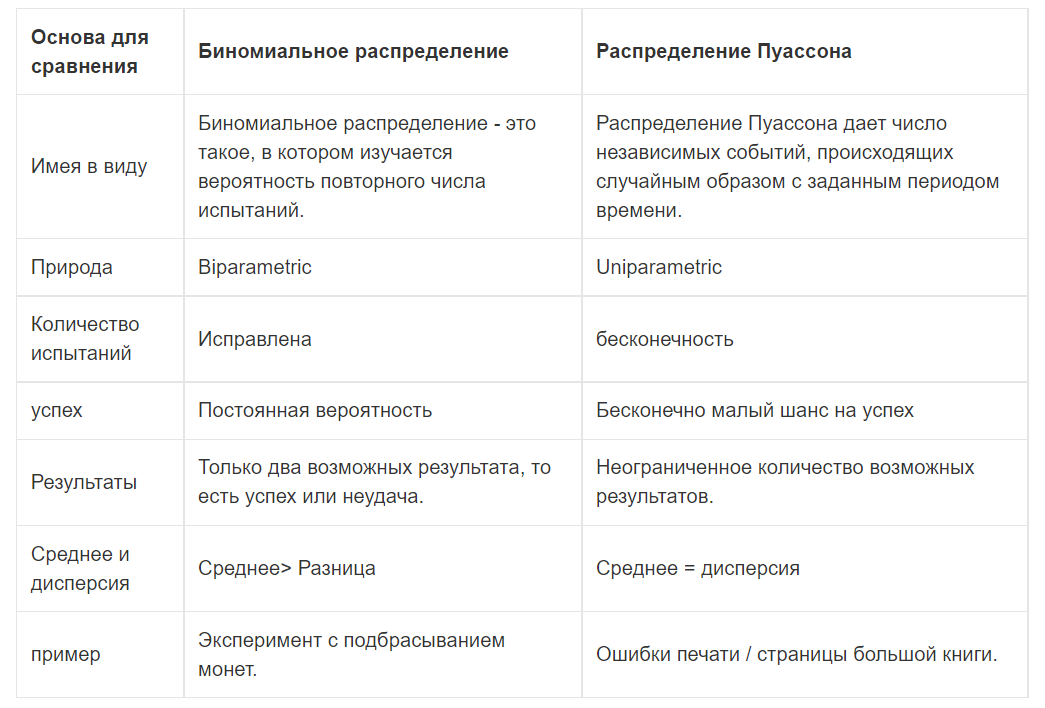 На всякий случай: http://stratum.ac.ru/education/textbooks/modelir/lection27.html №4.Равномерное распределение. Показательное распределение.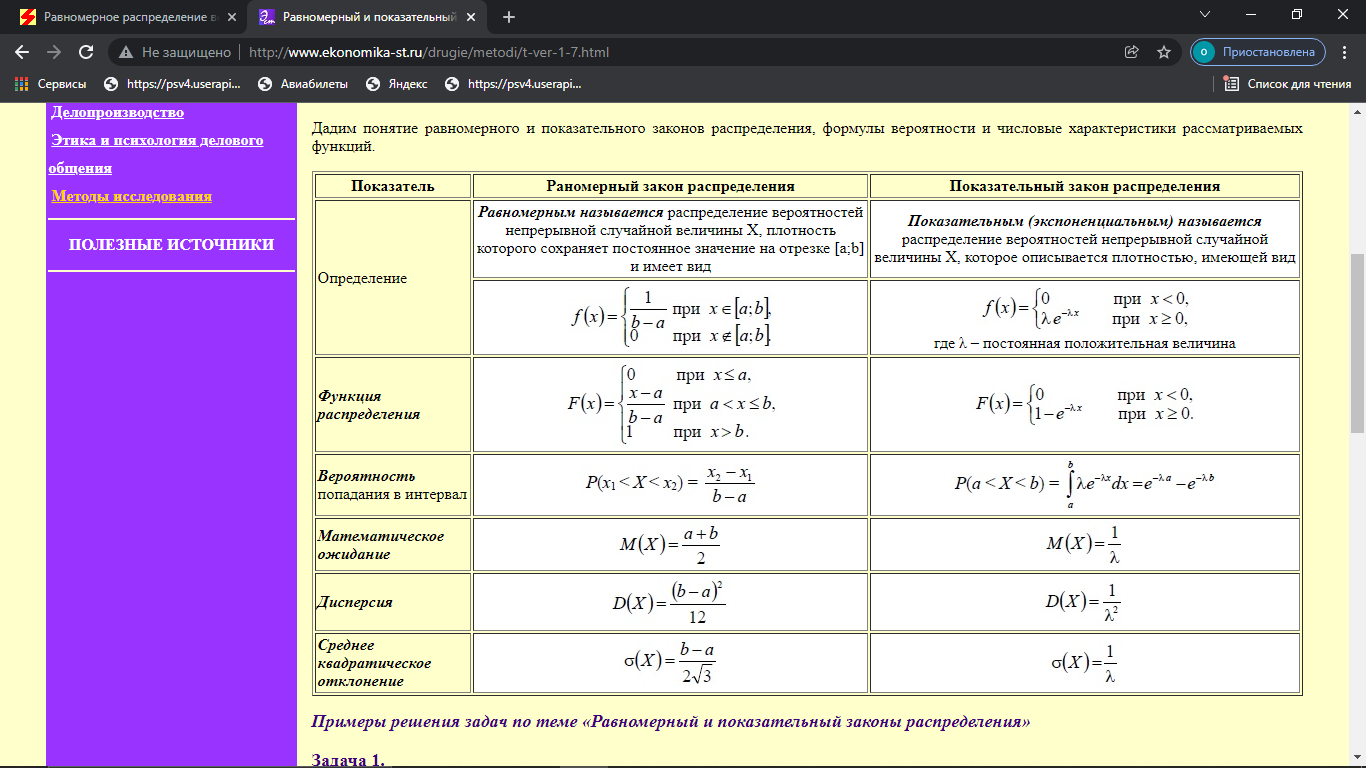 №5.Гауссовское распределение.Норма́льное распределе́ние, также называемое распределением Гаусса или Гаусса — Лапласа — распределение вероятностей, которое в одномерном случае задаётся функцией плотности вероятности, совпадающей с функцией Гаусса: 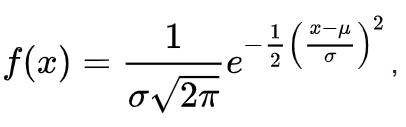 где параметр где параметр 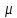 — математическое ожидание (среднее значение), медиана и мода распределения, а параметр — математическое ожидание (среднее значение), медиана и мода распределения, а параметр 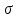 — среднеквадратическое отклонение, — среднеквадратическое отклонение, 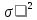 — дисперсия распределения. — дисперсия распределения.Определения Стандартное нормальное распределениеНаиболее простой случай нормального распределения — стандартное нормальное распределение — частный случай, когда 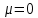 и и 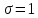 . .Его плотность вероятности равна: 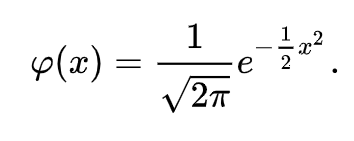 Множитель 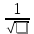 в выражении обеспечивает условие нормировки интеграла в выражении обеспечивает условие нормировки интеграла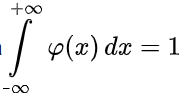 Поскольку множитель Поскольку множитель 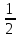 в экспоненте обеспечивает дисперсию равную единице, то и стандартное отклонение равно 1. Функция симметрична в точке х = 0, её значение в ней максимально и равно в экспоненте обеспечивает дисперсию равную единице, то и стандартное отклонение равно 1. Функция симметрична в точке х = 0, её значение в ней максимально и равно 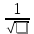 . Точки перегиба функции: х = +1 и х = -1. Гаусс называл стандартным нормальным распределение с . Точки перегиба функции: х = +1 и х = -1. Гаусс называл стандартным нормальным распределение с 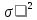 = 1 / 2 то есть: = 1 / 2 то есть: 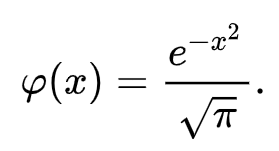 Нормальное распределение с параметрами 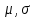 Каждое нормальное распределение — это вариант стандартного нормального распределения, область значений которого растягивается множителем 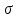 (стандартное отклонение) и переносится на (стандартное отклонение) и переносится на 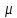 (математическое ожидание): (математическое ожидание):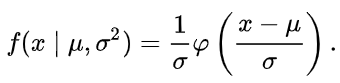 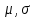 являются параметрами нормального распределения. Плотность вероятности должна нормироваться являются параметрами нормального распределения. Плотность вероятности должна нормироваться 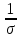 , так что интеграл равен 1. Если Z — стандартная нормальная случайная величина, то величина , так что интеграл равен 1. Если Z — стандартная нормальная случайная величина, то величина 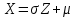 будет иметь нормальное распределение с математическим ожиданием будет иметь нормальное распределение с математическим ожиданием 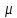 и стандартным отклонением и стандартным отклонением 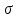 . Наоборот, если X — нормальная величина с параметрами . Наоборот, если X — нормальная величина с параметрами 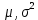 , то , то 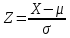 будет иметь стандартное нормальное распределение. будет иметь стандартное нормальное распределение.Свойства МоментыМоментами и абсолютными моментами случайной величины Х называются математические ожидания случайных величин 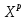 и и 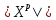 , соответственно. Если математическое ожидание случайной величины , соответственно. Если математическое ожидание случайной величины 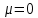 , то эти параметры называются центральными моментами. В большинстве случаев представляют интерес моменты для целых p. Если X имеет нормальное распределение, то для неё существуют (конечные) моменты при всех p с действительной частью больше −1. Для неотрицательных целых p центральные моменты таковы: , то эти параметры называются центральными моментами. В большинстве случаев представляют интерес моменты для целых p. Если X имеет нормальное распределение, то для неё существуют (конечные) моменты при всех p с действительной частью больше −1. Для неотрицательных целых p центральные моменты таковы: 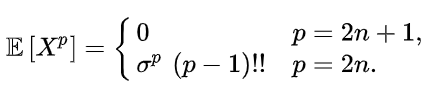 Здесь n — натуральное число, а запись (p - 1)!! означает двойной факториал числа p - 1 то есть (поскольку p - 1 в данном случае нечётно) произведение всех нечётных чисел от 1 до p - 1. Центральные абсолютные моменты для неотрицательных целых p таковы: 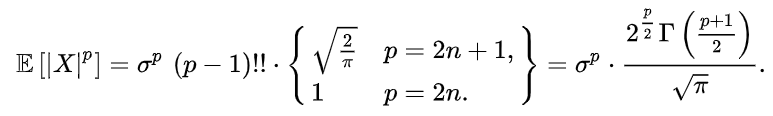 Последняя формула справедлива также для произвольных p > -1. Преобразование Фурье и характеристическая функцияПреобразование Фурье нормальной плотности вероятности 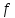 с математическим ожиданием с математическим ожиданием 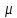 стандартным отклонением стандартным отклонением 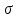 равно: равно: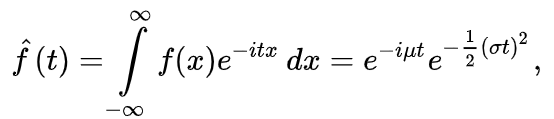 где i есть мнимая единица. где i есть мнимая единица.Если математическое ожидание 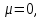 то первый множитель равен 1, и преобразование Фурье, с точностью до константы есть нормальная плотность вероятности на частотных интервалах, с математическим ожиданием равным 0 и стандартным отклонением то первый множитель равен 1, и преобразование Фурье, с точностью до константы есть нормальная плотность вероятности на частотных интервалах, с математическим ожиданием равным 0 и стандартным отклонением 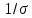 . В частности, стандартное нормальное распределение . В частности, стандартное нормальное распределение 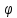 есть собственная функция от преобразования Фурье. есть собственная функция от преобразования Фурье.В теории вероятности, преобразование Фурье плотности распределения действительной случайной величины X близко связано с характеристической функцией 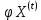 этой величины, которая определена как математическое ожидание от этой величины, которая определена как математическое ожидание от 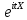 и является функцией вещественной переменной t (частотный параметр преобразования Фурье). Определение может быть распространено и на комплексную переменную t. Соотношение записывается так: и является функцией вещественной переменной t (частотный параметр преобразования Фурье). Определение может быть распространено и на комплексную переменную t. Соотношение записывается так:Бесконечная делимостьНормальное распределение является бесконечно делимым. Если случайные величины X1 и X2 независимы и имеют нормальное распределение с математическими ожиданиями 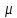 1 и 1 и 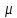 2 и дисперсиями 2 и дисперсиями 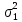 и и 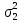 соответственно, то X1+X2 также имеет нормальное распределение с математическим ожиданием соответственно, то X1+X2 также имеет нормальное распределение с математическим ожиданием 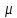 1+ 1+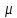 2 и дисперсией 2 и дисперсией 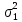 + +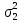 . .Отсюда вытекает, что нормальная случайная величина представима как сумма произвольного числа независимых нормальных случайных величин. Максимальная энтропияНормальное распределение имеет максимальную дифференциальную энтропию среди всех непрерывных распределений, дисперсия которых не превышает заданную величину. Правило трёх сигм для гауссовской случайной величиныПравило трёх сигм ( 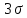 ) — практически все значения нормально распределённой случайной величины лежат в интервале: ( ) — практически все значения нормально распределённой случайной величины лежат в интервале: (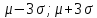 ), где ), где 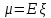 — математическое ожидание и параметр нормальной случайной величины. — математическое ожидание и параметр нормальной случайной величины.Более точно — приблизительно с вероятностью 0,9973 значение нормально распределённой случайной величины лежит в указанном интервале. |
