Вопросы. вопросы. 1. Вероятность. Вероятностное пространство. Свойства
 Скачать 6.39 Mb.
|
№6.Геометрическое распределение.   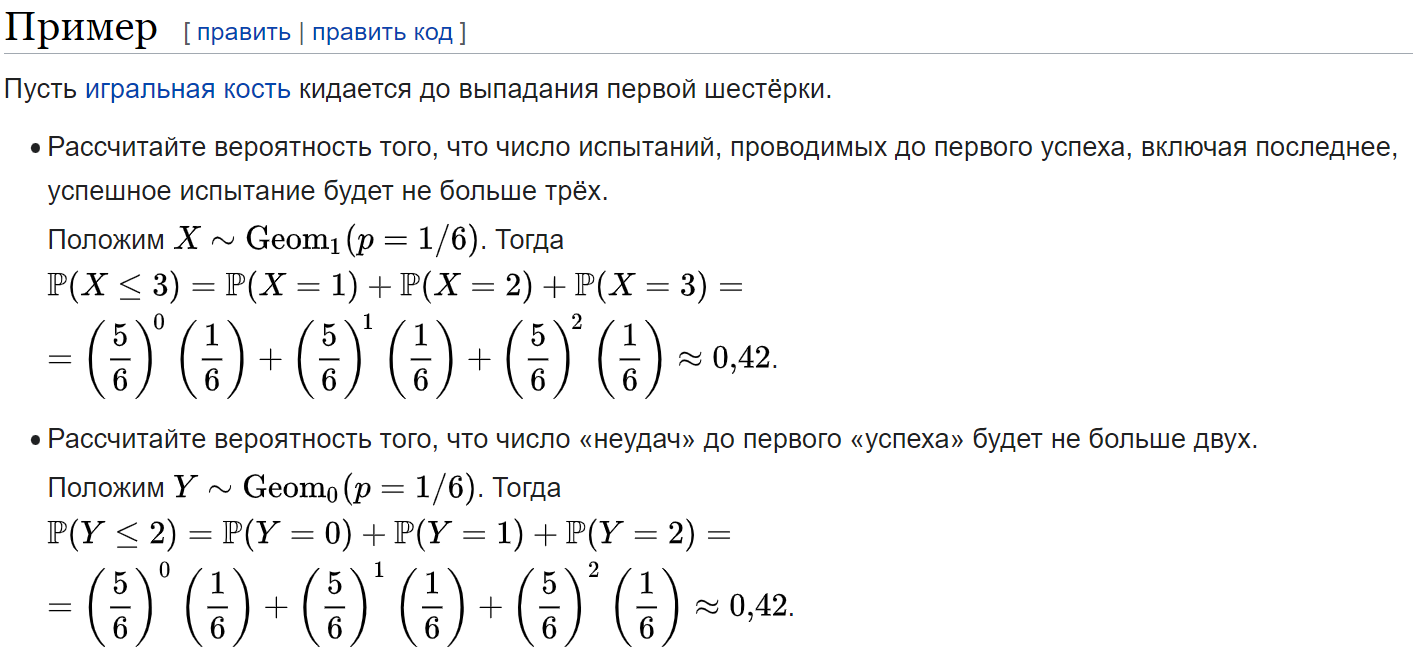 №7.Характеристические функции. Свойства. Характеристическая функция — такая термодинамическая функция, по изменению которой в определенных условиях можно судить о направленности самопроизвольного процесса и о достижении состояния равновесия, а производные различного порядка которых дают нам явно и наиболее просто другие термодинамические функции и параметры системы. 
Свойство 1.Характеристическая функция всегда существует |φξ(t)|=|Meitξ|≤M|eitξ|=M1=1 Свойство 2. По характеристической функции однозначно восстанавливается распределение (функция распределения, а также плотность или таблица распределения). То есть если две случайные величины имеют одинаковые характеристические функции, то и распределения этих случайных величин совпадают. Формулы, с помощью которых это делается, в анализе называют формулами «обратного преобразования Фурье». Например, если модуль характеристической функции интегрируем на всей прямой, то у случайной величины есть плотность распределения Свойство 3. Характеристическая функция случайной величины а+bξ связана с характеристической функцией случайной величины равенством φа+bξ(t)=Meit (а+bξ)=eitа φξ(tb). Свойство 4. Характеристическая функция суммы независимых случайных величин равна произведению характеристических функций слагаемых: если случайные величины ξ и η независимы, то, по свойству математических ожиданий φξ+η(t)=Meit(ξ+η)=MeitξMeitη=φξ(t)φη(t). Свойство 5. Пусть существует момент порядка k=1,2,... случайной величины ξ, то есть M|ξ|k<∞. Тогда ее характеристическая функция φξ(t)непрерывно дифференцируема k раз, и ее k-япроизводная в нулесвязана с моментом порядка k равенством: = 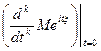 =  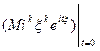=ikMξk..Свойство 6. Пусть существует момент порядка k=1,2,... случайной величины ξ, то есть M|ξ|k<∞. Тогда ее характеристическая функция φξ(t)в окрестности точки t=0 разлагается в ряд Тейлора №8. Сходимость по распределению. Критерий на основе характеристических функций.Пусть дано вероятностное пространство 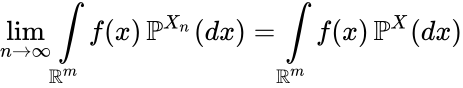 и опеделённые на нём случайные величины  . Каждая случайная величина индуцирует вероятностную меру на  , называемую её распределением.Случайные величины  сходятся по распределению к случайной величине , если распределения  слабо сходятся к распределению  , то есть для любой ограниченной борелевской функции  .Свойства характерических функций: 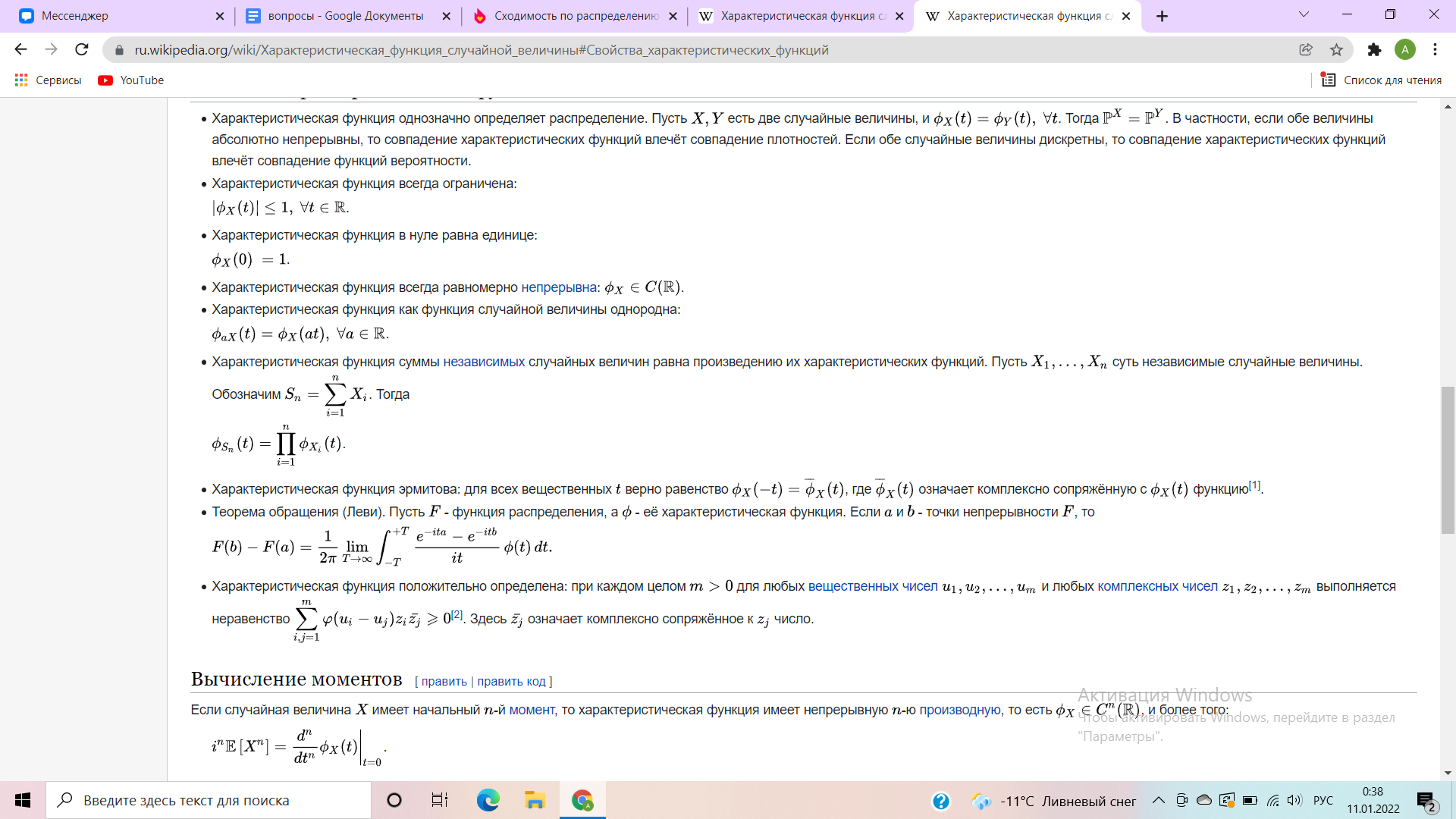 |