Вопросы. вопросы. 1. Вероятность. Вероятностное пространство. Свойства

• Название: 1. Вероятность. Вероятностное пространство. Свойства
• Анкор: Вопросы
• Дата: 14.02.2022
• Размер: 6.39 Mb.
• Имя файла: вопросы.docx
• Тип: Документы; #360876
• страница: 6 из 8

№14.Кореляция. Коэффициент кореляции. Корелляционная матрица.

Корреля́ция (от лат. correlatio «соотношение»), или корреляцио́нная зави́симость — статистическая взаимосвязь двух или более случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин.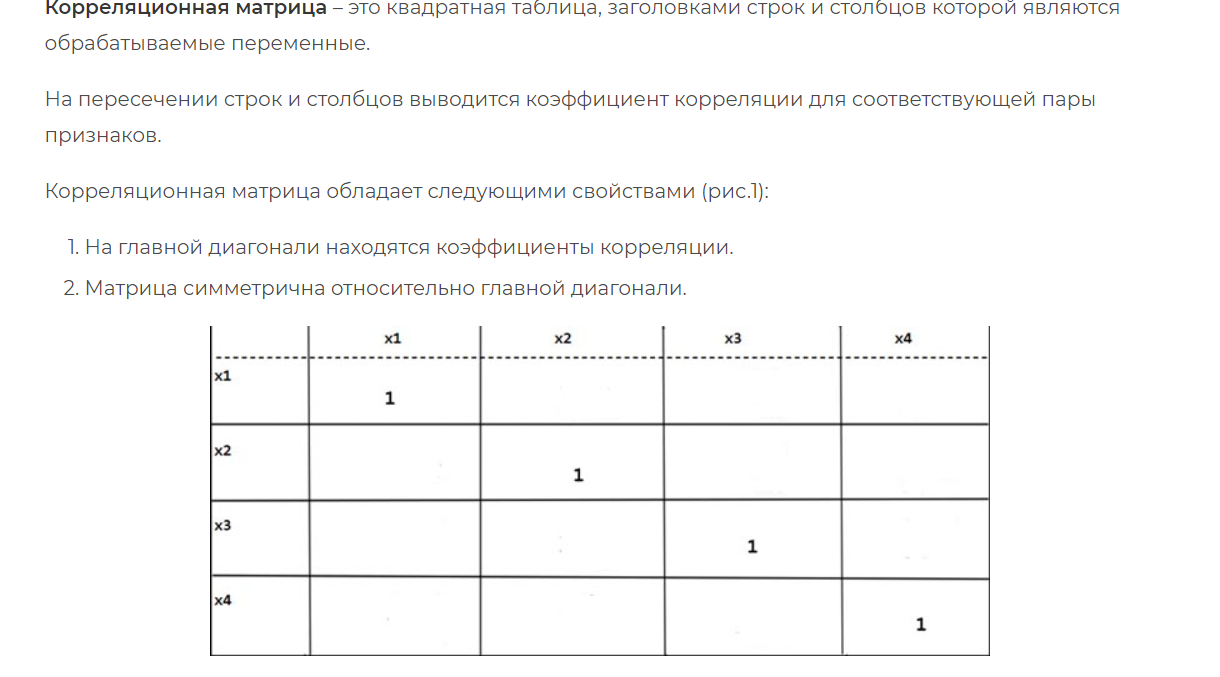

№15.Случайные величины. Свойства. Независимость случайных величин.

Случайной величиной называется такая величина, которая случайно принимает какое-то значение из множества возможных значений.

Случайные величины обозначаются: X, Y, Z, ... Значения, которые они принимают: x,y,z.

Один из примеров случайной величины:

X – количество очков, которое выпадет после броска игрального кубика.

В результате данного испытания выпадет одна и только грань, какая именно – не предсказать (фокусы не рассматриваем); при этом случайная величина X может принять одно из следующий значений:

По множеству возможных значений различают дискретные и непрерывные случайные величины.

Дискретными называются случайные величины, значениями которых являются только отдельные точки числовой оси. (Число их может быть как конечно, так и бесконечно).

Пример: Число родившихся девочек среди ста новорожденных за последний месяц - это дискретная случайная величина, которая может принимать значения 1,2,3, …

Непрерывными называются случайные величины, которые могут принимать все значения из некоторого числового промежутка.

Пример: Расстояние, которое пролетит снаряд при выстреле - это непрерывная случайная величина, значения которой принадлежат некоторому промежутку [а; в].

Независимость случайных величин:

Случайные величины ξξ и ηη называются независимыми, если ∀α,β∈R∀α,β∈R события [ξ⩽α][ξ⩽α] и [η⩽β][η⩽β] независимы.

P((ξ⩽α)∩(η⩽β))=P(ξ⩽α)⋅P(η⩽β)

Иначе говоря, в теории вероятностей две случайные величины называют независимыми, если известное значение одной из них не дает информации о другой.

№16.Функции распределения. Свойства. Плотность. Свойства. Моменты.

Фу́нкция распределе́ния — функция, характеризующая распределение случайной величины или случайного вектора; вероятность того, что случайная величина X примет значение, меньшее х, где х — произвольное действительное число.

Свойства функции распределения

1) значения функции распределения принадлежат отрезку [0, 1].



2) F(x) - неубывающая функция.



3) Вероятность того, что случайная величина примет значение, заключенное в интервале (а, b) , равна приращению функции распределения на этом интервале.



4) На минус бесконечности функция распределения равна нулю, на плюс бесконечности функция распределения равна единице.

5) Вероятность того, что непрерывная случайная величина X примет одно определенное значение, равна нулю.

Плотность распределения вероятностей непрерывной случайной величины Х есть функция f(x) – первая производная от функции распределения F(x).

Основные свойства плотности распределения.

1. Плотность распределения есть неотрицательная функция:



2. Интеграл в бесконечных пределах от плотности распределения равен единице: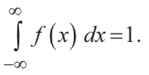

Момент распределения — средняя арифметическая различных степеней отклонений индивидуальных значений признака от определенной постоянной величины.

Общая формула расчета моментов распределения:



где А — постоянная величина, от которой определяется отклонение; а — степень отклонения (порядок момента).

В зависимости от выбора постоянной величины А различают три вида моментов:

1. Начальные (при А = 0):



2. Центральные (при А = х):



3. Условные (при А Ф 0 или х):



Анализируя формулы моментов распределения, можно сделать следующие выводы:

• 
  1. Начальный момент первого порядка представляет собой среднюю арифметическую и используется как показатель центра распределения.
  
• 
  2. Центральный момент:
  
  • 
    • первого порядка (в соответствии с нулевым свойством средней арифметической) всегда равен нулю;
    
  • 
    • второго порядка представляет дисперсию;
    
  • 
    • третьего порядка равен нулю в симметричном распределении и используется для определения показателя асимметрии (при изучении формы распределения);
    
  • 
    • четвертого порядка применяется при вычислении показателя эксцесса (при изучении формы распределения).
    

3. Условные моменты, также как и начальные моменты второго, третьего и четвертого порядков, самостоятельного значения не имеют, а используются для упрощения вычислений центральных моментов.