Контрольная работа дисциплина Эконометрика (продвинутый уровень) Ф. И. О студента Боярова Юлия Сергеевна
 Скачать 429.65 Kb. Скачать 429.65 Kb.
|
1.3. Текст ситуационной (практической задачи) № 2. 1. Оценить с помощью уравнения регрессии отвечают ли средства, передаваемые из областного бюджета органам местного самоуправления цели внутрирегионального выравнивания путем оценки следующего уравнения регрессии: 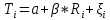 где Ti – перечисления из областного бюджета i-му муниципальному образованию в расчете на душу населения, 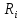 – налоговые и неналоговые доходы i-того муниципалитета на д.н., – налоговые и неналоговые доходы i-того муниципалитета на д.н., 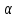 – свободный член регрессии, – свободный член регрессии, 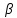 – угловой коэффициент, – угловой коэффициент, 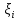 – остатки регрессии. – остатки регрессии. Результаты оценки представить с помощью таблицы. 2. Оценить наличие и направления действия стимулов для муниципалитетов Новосибирской области к увеличению налоговых доходов, собираемых на территориях, с помощью уравнения регрессии: 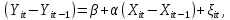 где Yit – располагаемые доходы i-го муниципального образования в году t, Xit – налоговые доходы i-го муниципального образования в году t, 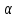 - угловой коэффициент, - угловой коэффициент, 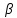 - константа, - константа, 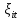 – остатки регрессии. – остатки регрессии. 3. Построить кривые Лоренца по каждому рассматриваемому периоду. 4. Рассчитать коэффициент фондов и индекс Джинни. 1.4. Ответ на практическую задачу № 2. 1. Оценить с помощью уравнения регрессии отвечают ли средства, передаваемые из областного бюджета органам местного самоуправления цели внутрирегионального выравнивания путем оценки следующего уравнения регрессии: 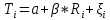 Ti = 2716,615 - 0,865 * Ri + 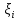 – уравнение регрессии для 1 периода – уравнение регрессии для 1 периодаTi = 2951,817 - 0,682 * Ri + 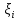 – уравнение регрессии для 2 периода. – уравнение регрессии для 2 периода.Таблица 6 – Результаты оценки средств с помощью уравнения регрессии для 1 и 2 периода
Таким образом, была произведена оценка средств с помощью уравнения регрессии для 2 периодов, в результате которой было выявлено следующее: значение показателя а в 1 периоде равно 2716,62 и имеет диапазон от 2299,37 до 3133,86, в котором он будет находиться с вероятностью 95%. Его значение выросло во 2 периоде на 235,2. с вероятностью 95% значение показателя b находится в интервале от - 1,2151 до - 0,5157, значение которого удовлетворяет данный интервал и соответственно составляет - 0,8654. Значение также возросло и составило - 0,6818. 2. Оценить наличие и направления действия стимулов для муниципалитетов Новосибирской области к увеличению налоговых доходов, собираемых на территориях, с помощью уравнения регрессии: 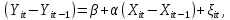 (Yit – Yit-1) = -2142,28 + 2,156 (Xit – Xit-1) + ξit – уравнение регрессии для муниципалитетов Новосибирской области к увеличению налоговых доходов Таблица 7 – Результаты оценки средств с помощью уравнения регрессии для 1 и 2 периода
Таким образом, можно судить о том, что с вероятностью 95% значение показателя b находится в интервале от 2,081 до 2,231, значение которого удовлетворяет данный интервал и соответственно составляет 2,156. В свою очередь, значение показателя а также имеет диапазон от -8511,515-4226,950, в котором он будет находиться с вероятностью 95%. 3. Построить кривые Лоренца по каждому рассматриваемому периоду 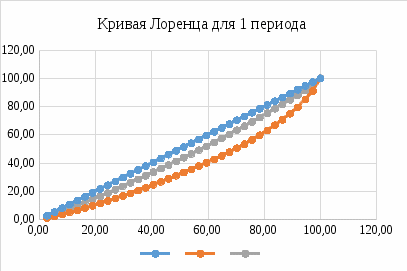 Рисунок 13 – График кривой Лоренца для 1 период 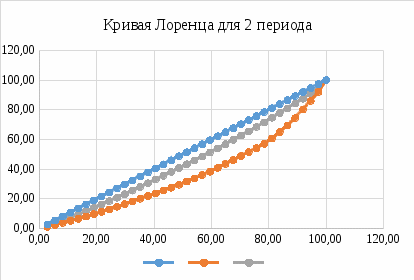 Рисунок 14 – График кривой Лоренца для 2 период Ряд 1 – линия «абсолютного равенства»; Ряд 2 – внутрирегиональное распределение бюджетных доходов на душу населения без учета финансовой помощи из областного бюджета; Ряд 3 – внутрирегиональное распределение бюджетных доходов на душу населения с учетом финансовой помощи из областного бюджета. Таким образом, кривая Лоренца отражает кумулятивные (накопленные) доли дохода населения, а также это кривая, показывающая степень неравенства распределения доходов людей или домашних хозяйств. Чем круче выгнут «лук Лоренца», тем сильнее неравенство. В свою очередь, степень неравенства в доходах определяется коэффициентом Джинни 4. Рассчитать коэффициент фондов и индекс Джинни. Значения коэффициента фондов и индекса Джинни, рассчитанные для полученных и располагаемых бюджетных доходов муниципальных образований Новосибирской области, приведены в таблице 8. Таблица 8 – коэффициент фондов и индекс Джинни, рассчитанные для муниципальных районов и городских округов Новосибирской области
Индекс Джини показывает концентрацию доходов по группам территорий. Он дает представление о том, в пользу каких территорий работает распределительный механизм: либо доходы относительно равномерно распределяются среди территорий, либо основную выгоду получает узкий круг территорий, и концентрация доходов носит ярко выраженный характер. Соответственно, чем больше значение индекса Джини, тем больше неравенство между территориями. Коэффициент Джини может принимать значения от 0 до 1. Чем ближе коэффициент Джини к нулю, тем меньше изгиб кривой Лоренца, и доходы распределены более равномерно. Чем ближе коэффициент Джини к единице, тем больше изгиб кривой Лоренца, и доходы распределены менее равномерно. Тест Вариант 4 1. Укажите или напишите правильный ответ: Параметр β0i в модели yit = β0i + β1Xit + uit включает: + А) характеристики объекта наблюдения, которые меняются во времени; Б) характеристики объекта неизменные во времени; В) характеристики различных объектов наблюдения в один момент времени. 2. Укажите или напишите правильный ответ: Набор данных по одному объекту наблюдения в различные периоды времени называется: + А) временным рядом; Б) сбалансированными данными; В) ротационной панелью. 3. Укажите или напишите все правильные ответы: Панельная смертность при анализе панельных данных приводит к: + А) смещенным оценкам; Б) несостоятельным оценкам; В) неэффективным оценкам; Г) невозможности оценить уравнение регрессии. 4. Укажите или напишите правильный ответ: Для получения оценок модели со случайными эффектами необходимо использовать: А) косвенный метод наименьших квадратов; + Б) выполнимый обобщенный метод наименьших квадратов; В) двухшаговый метод наименьших квадратов; Г) обычный метод наименьших квадратов. 5. Укажите или напишите все правильные ответы: Из предпосылки о том, что условное математическое ожидание E[uit|xit] для уравнения yit = μit + x’it β + uit равно нулю, следует, что: А) регрессоры и остатки не коррелируют между собой; + Б) регрессоры и остатки взаимосвязаны; В) для любой функции g, не равной константе, остатки uit и g(xit) не коррелируют между собой; Г) для любой функции g, не равной константе, остатки uit и g(xit) взаимосвязаны. 6. Укажите или напишите правильный ответ: Проверка модели на наличие случайных эффектов проводится с помощью: + А) теста множителей Лагранжа; Б) теста Хаусмана; В) F-теста. 7. Укажите или напишите правильный ответ: Параметрами, которые определяют среднее местоположение yit, если все регрессоры зафиксированы на нулевом уровне для уравнения yit = μit + x’it β + uit, являются параметры: А) yit Б) μit + В) xit Г) βit Д) uit 8. Укажите или напишите правильный ответ: Оценка параметра наклона модели с фиксированными эффектами называется: + А) оценкой с учетом вариации между объектами наблюдения; Б) оценкой с учетом вариации в рамках объекта наблюдения В) оценкой объединенной модели; Г) SUR-оценкой. 9. Укажите или напишите все правильные ответы: Для получения модели с фиктивными переменными из модели вида yit = μit + x’it β + uit необходимо сделать следующие предположения: А) μit = μ, βit = β для всех i, t; Б) μit = μi, βit = βi для всех i, t; + В) Zi = (yi, Xi) i.i.d при E[uit|Xi] = 0 и E[u2it|Xi] = σ2; Г) Zi = (yi, Xi) i.i.d при E[uit|Xi] = 0 и E[u2it|xit] = 0 для всех i, t; E[uitujs|xitxjs] = σit если t = s и E[uitujs|xitxjs] = 0 если t ≠ s; Д) μit = μi, βit = β для всех i, t. 10. Укажите или напишите все правильные ответы: Для моделирования гетерогенности в модели yit = μit + x’it β + uit необходимо сделать следующие предположения: А) μit = μ, βit = β для всех i, t; Б) μit = μi, βit = βi для всех i, t; + В) Zi = (yi, Xi) i.i.d при E[uit|Xi] = 0 и E[u2it|Xi] = σ2; Г) Zi = (yi, Xi) i.i.d при E[uit|Xi] = 0 и E[u2it|xit] = 0 для всех i, t; E[uitujs|xitxjs] = σit если t = s и E[uitujs|xitxjs] = 0 если t ≠ s; Д) μit = μi, βit = β для всех i, t. Список используемых источников Базилевский М.П., Гефан Г.Д. Эконометрика (продвинутый уровень): учебное пособие / М.П. Базилевский, Г.Д. Гефан. – Иркутск: ИрГУПС, 2019. – 108 с. Ратникова Т.А. Введение в эконометрический анализ панельных данных. ЭЖ ВШЭ, т.10, №2 - 4, 2017 Бабайцев, В. А. Математические методы финансового анализа : учеб. пособие для вузов / В. А. Бабайцев, В. Б. Гисин. — 2-е изд., испр. и доп. — М. : Издательство Юрайт, 2019. — 215 с. Дубина И.Н. Математико-статистические методы в эмпирических социально-экономических исследованиях. – М.: Финансы и статистика, 2017. – 416 с. Елисеева И.И. Практикум по эконометрике: Учебное пособие. – М.: Финансы и статистика, 2017 - 192 с. Елисеева И.И. Эконометрика: учебник. – М.: Финансы и статистика, 2018 - 344 с. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
