ЭКОНОМЕТРИКА2. Контрольная работа по дисциплине Эконометрика Научный д э. н., проф. Соловьев Юрий Павлович Москва 2011
 Скачать 71.98 Kb. Скачать 71.98 Kb.
|
Установка продолжительности отчетных динамических рядов дает возможность определить число факторов, подлежащих включению в модель. На каждый фактор модели должно приходиться не менее 5 точек наблюдения, тогда влияние факторов на результирующий показатель можно назвать неслучайным. В нашем случае продолжительность рядов составляет 16 точек наблюдений (т.е. 16 лет) и мы можем взять не более 3 факторов, которые можно включить в модель. На основе коэффициента парной корреляции рассчитаем взаимозависимости между зависимой (У) и переменными (х1, х2, х3, х4), а также переменных между собой. 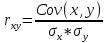  Результаты расчетов представлены в таблице 3. Табл.3.
В модель можно выбрать 3 фактора. Так как коэффициент парной корреляции между факторами х3 и х4 минимален, то включаем их в модель. Максимально возможное число факторов модели равно 3, однако, добавление любого из оставшихся факторов невозможно, в связи с их сильной взаимозависимостью.
Для определения оценок b0, b1, b2 воспользуемся матричным МНК. Представим данные наблюдений и коэффициенты в матричном виде. Тогда вектор оценок коэффициентов регрессии найдем по формуле В = (Хт Х)-1 Хт У
XТ=
ХТ*Х =
(ХТ*Х)-1 =
ХТ*У =
В = ((ХТ*Х)-1) ХТ*У = Следовательно коэффициенты регрессии следующие: b0 = - 1702; b1 = 175,62; b2 = 86,79. Уравнение регрессии имеет вид: У = -1702 + 175,62*Х1 + 86,79*Х2 , где Х1 – валовой сбор овощей Х2 – время
Применение МНК для получения оценок параметров предполагает выполнение следующих предпосылок:
Тест на гомоскедастичность. Одной из предпосылок является предположение о постоянстве дисперсий случайных отклонений во времени (гомоскедастичность). Для проверки гипотезы о присутствии гомоскедастичности проводится тест ранговой корреляции Спирмена. Выдвигается нулевая гипотеза об отсутствии гетероскедостичности случайного члена и рассчитывается коэффициент r по формуле: 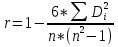
Тогда Р=1-(6*654)/(16*255)=0.03. Если r 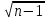 ≥ tтабл., то гипотеза об отсутствии гетероскедастичности отклоняется. Так как r ≥ tтабл., то гипотеза об отсутствии гетероскедастичности отклоняется. Так как r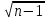 = 0,116 < tтабл. = 0,425, то гипотеза об отсутствии гетероскедастичности не отклоняется. = 0,116 < tтабл. = 0,425, то гипотеза об отсутствии гетероскедастичности не отклоняется. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
