Контрольная работа. Контрольная работа по дисциплине Эконометрика

• Название: Контрольная работа по дисциплине Эконометрика
• Дата: 03.07.2022
• Размер: 397.5 Kb.
• Имя файла: Контрольная работа.doc
• Тип: Контрольная работа; #623241

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное

образовательное учреждение высшего образования

«Челябинский государственный университет»

(ФГБОУ ВО «ЧелГУ»)
ФАКУЛЬТЕТ ЗАОЧНОГО И ДИСТАНЦИОННОГО ОБУЧЕНИЯ


КОНТРОЛЬНАЯ РАБОТА

по дисциплине «Эконометрика»

Вариант № 3
Выполнил студент

________________________ ,

Группа ____________ ,

заочная форма обучения,

направление подготовки

38.03.01 Экономика

Проверил

____________________________

Должность: __________________

Ученая степень: ______________

Ученое звание: _______________

Челябинск

2022

Исходные данные

Имеются данные о часовом заработке одного рабочего (Y) и общем стаже работы после окончания учебы (Х).

№	Часовой заработок одного рабочего, долл./час	Общий стаж работы после окончания учебы, лет
1	22,4	53,4
2	8,9	8,0
3	13,3	18
4	18,3	29,5
5	13,8	32,0
6	11,7	14,7
7	19,5	13,0
8	15,2	11,3
9	14,4	18,0
10	22,0	11,8
11	16,4	32
12	18,9	16,0
13	16,1	29,5
14	13,3	23,1
15	17,3	55,0

Задания выполняются с использованием MS Excel, расчеты и графики необходимо вставлять в работу.

Задания

Исследовать зависимость часового заработка одного рабочего от общего стажа работы после окончания учебы путем построения уравнения парной линейной регрессии

.

Предварительный анализ данных:

1. 
   Вычислите и проанализируйте описательные статистики (выборочные средние, медиану, моду, среднее квадратическое отклонение) для переменных X, Y.
   
2. 
   Постройте поле корреляции (диаграмму рассеяния) и сформулируйте гипотезу о форме связи.
   
3. 
   Вычислите парный коэффициент корреляции между переменными. Интерпретируйте полученные результаты: соответствуют ли знаки коэффициента вашим ожиданиям?
   
4. 
   Найдите оценки и параметров модели парной линейной регрессии и . Запишите полученное уравнение регрессии.
   
5. 
   Проверьте значимость оценок коэффициентов и с надежностью 0,95 с помощью t-статистики Стьюдента и сделать выводы о значимости этих оценок. Значимо ли уровень образования влияет на заработок?
   
6. 
   Определите интервальные оценки коэффициентов и с надежностью 0,95. Сделайте вывод о точности полученных оценок коэффициентов.
   
7. 
   Рассчитайте стандартную ошибку регрессии. Сделайте вывод о точности полученного уравнения регрессии.
   
8. 
   Определите коэффициент детерминации R² и сделайте вывод о качестве подгонки уравнения регрессии к исходным данным.
   
9. 
   Рассчитайте среднюю ошибку аппроксимации и сделайте выводы о качестве уравнения регрессии.
   
10. 
    Рассчитайте прогнозное значение результата , если значение фактора X будет больше на 15% его среднего уровня .
    
11. 
    Дайте экономическую интерпретацию коэффициентов парной регрессии.
    

Решение:

Исследуем зависимость часового заработка одного рабочего от общего стажа работы после окончания учебы путем построения уравнения парной линейной регрессии

.

Предварительный анализ данных:

1. 
   Вычислим и проанализируем описательные статистики (выборочные средние, медиану, моду, среднее квадратическое отклонение) для переменных X, Y.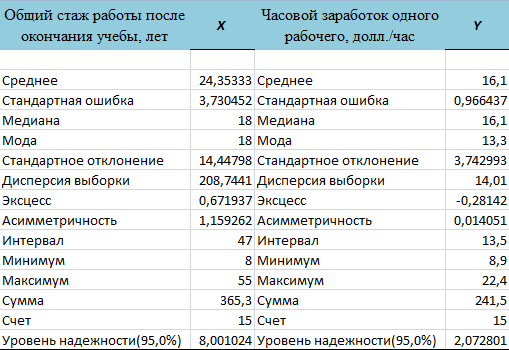
   

Определяем уровень варьирования признаков: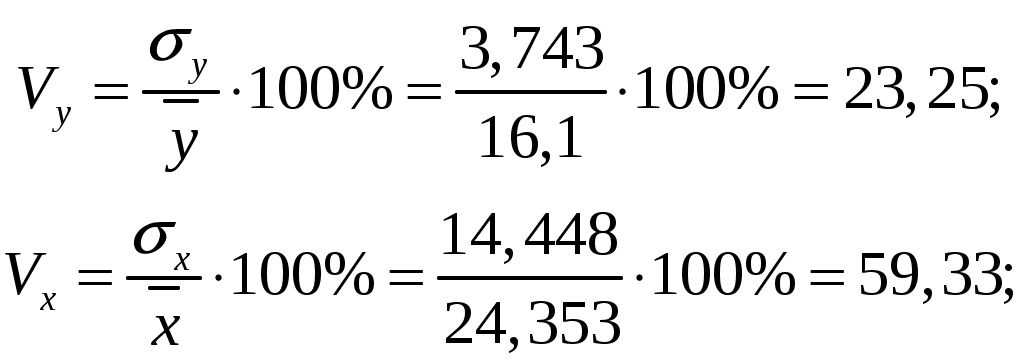



где σ_x – стандартное отклонение по x, а σ_y – стандартное отклонение по y,

- среднее арифметическое квадратов отклонений по x_, по y соответственно.

Приходим к выводу об умеренном уровне варьирования признака x, не превышающем 35% (т.е. совокупность данных по часовому заработку одного рабочего), и возможности применения метода наименьших квадратов (МНК) для их изучения.

2. 
   Построим поле корреляции (диаграмму рассеяния) и сформулируем гипотезу о форме связи.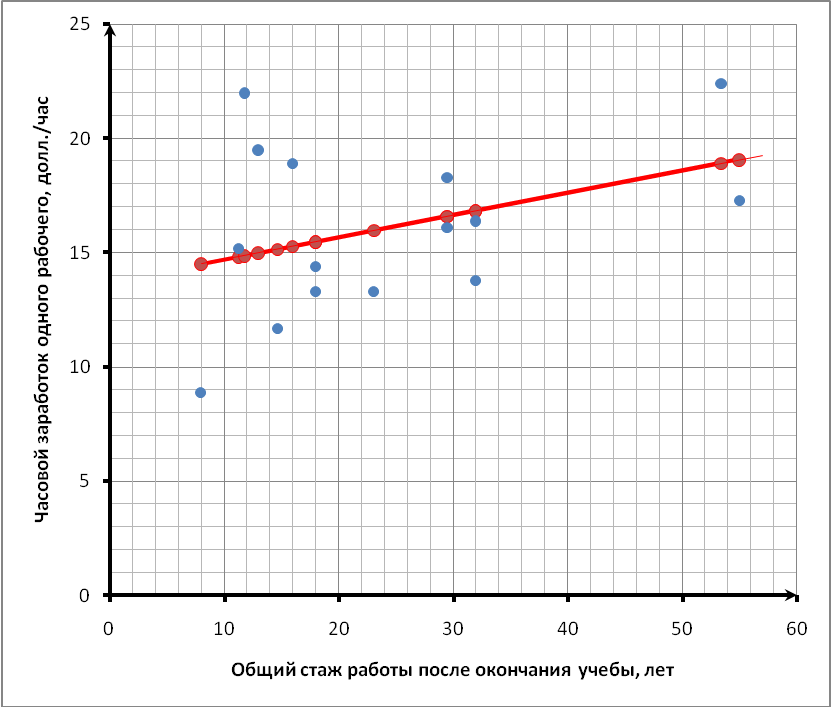
   

По расположению точек, их концентрации в определенном направлении можно судить о наличие умеренной связи. На основании поля корреляции можно выдвинуть гипотезу, что между факторным признаком и результативным признаком существует прямая, линейная связь.

3. 
   Вычислим парный коэффициент корреляции между переменными. Интерпретируйте полученные результаты: соответствуют ли знаки коэффициента вашим ожиданиям?
   

Линейный коэффициент корреляции характеризует тесноту линейной связи между изучаемыми признаками. Его можно определить по следующей формуле: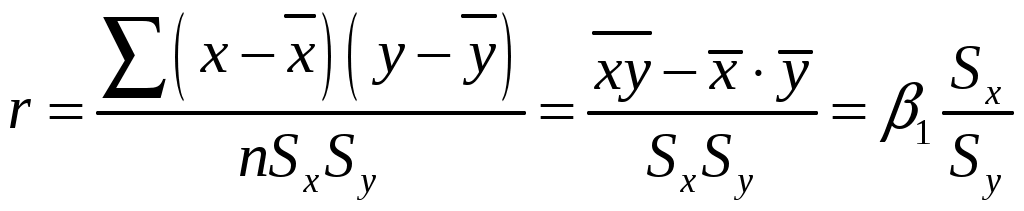

,

где ;

Вычислим :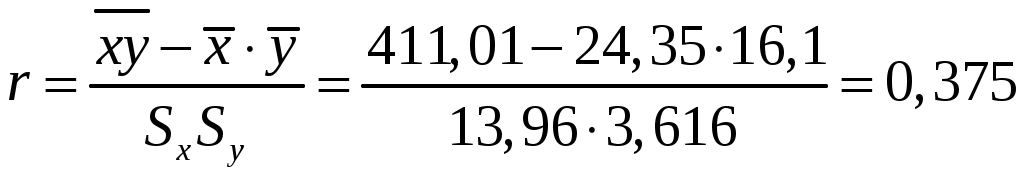

Значения линейного коэффициента корреляции принадлежит промежутку [-1;1]. Связь между признаками могут быть слабыми и сильными (тесными).

На практике обычно считается, что:

1) если 0,7 ≤ rxy ≤ 1, то связь тесная прямая;

2) 0,3 ≤ rxy < 0,7, то связь умеренная прямая;

3) –0,3 < rxy < 0,3, то связь слабая или отсутствует;

4) –0,7 < rxy ≤ –0,3, то связь умеренная обратная;

5) –1 ≤ rxy ≤ –0,7, то связь тесная обратная

Для нашей задачи r = 0,3725, что подтверждает вывод, сделанный ранее, что связь между признаками прямая, а также указывает на умеренную взаимосвязь между часовым заработком одного рабочего и общим стажем работы после окончания учебы. Положительная величина свидетельствует о прямой связи между изучаемыми признаками

Модель парной регрессии:

4. 
   Найдем оценки и параметров модели парной линейной регрессии и . Запишите полученное уравнение регрессии.
   

В общем виде однофакторная линейная эконометрическая модель записывается следующим образом:



где вектор наблюдений за результативным показателем;

вектор наблюдений за фактором;

неизвестные параметры, что подлежат определению;

случайная величина ( отклонение, остаток)

Ее оценкой является модель:

вектор оцененных значений результативного показателя ;

оценки параметров модели.

Чтобы найти оценки параметров модели воспользуемся 1МНК и составим таблицу 1:

Таблица 1

Вспомогательные расчеты

Номер региона
	53,4	22,4	1196,16	2851,56	501,76	18,92086
	8	8,9	71,2	64	79,21	14,51185
	18	13,3	239,4	324	176,89	15,483
	29,5	18,3	539,85	870,25	334,89	16,59982
	32	13,8	441,6	1024	190,44	16,8426
	14,7	11,7	171,99	216,09	136,89	15,16252
	13	19,5	253,5	169	380,25	14,99742
	11,3	15,2	171,76	127,69	231,04	14,83233
	18	14,4	259,2	324	207,36	15,483
	11,8	22	259,6	139,24	484	14,88089
	32	16,4	524,8	1024	268,96	16,8426
	16	18,9	302,4	256	357,21	15,28877
	29,5	16,1	474,95	870,25	259,21	16,59982
	23,1	13,3	307,23	533,61	176,89	15,97828
	55	17,3	951,5	3025	299,29	19,07625
Сумма	365,3	241,5	6165,14	11818,69	4084,29	241,5
Ср. знач.	24,35333	16,1	411,0093	787,9127	272,286	16,1

Найдем компоненты 1МНК :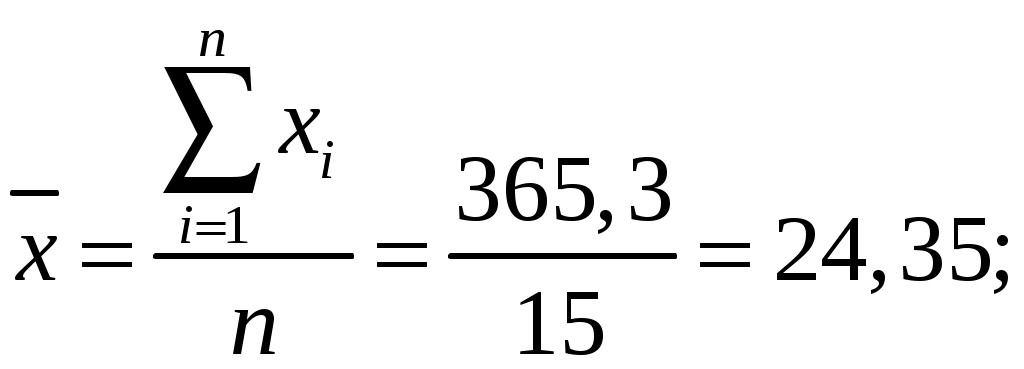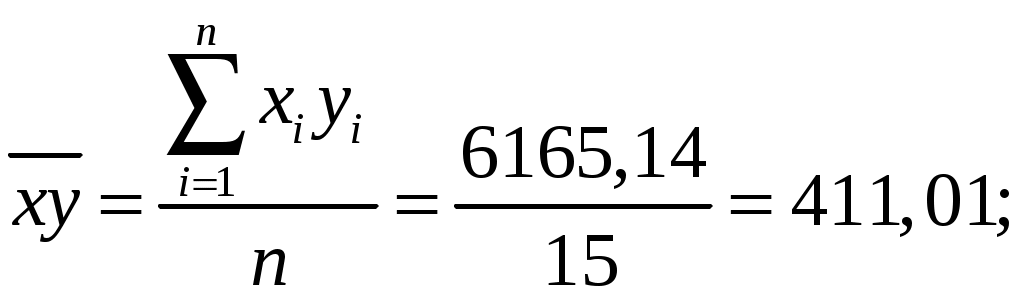







Находим оценки параметров модели: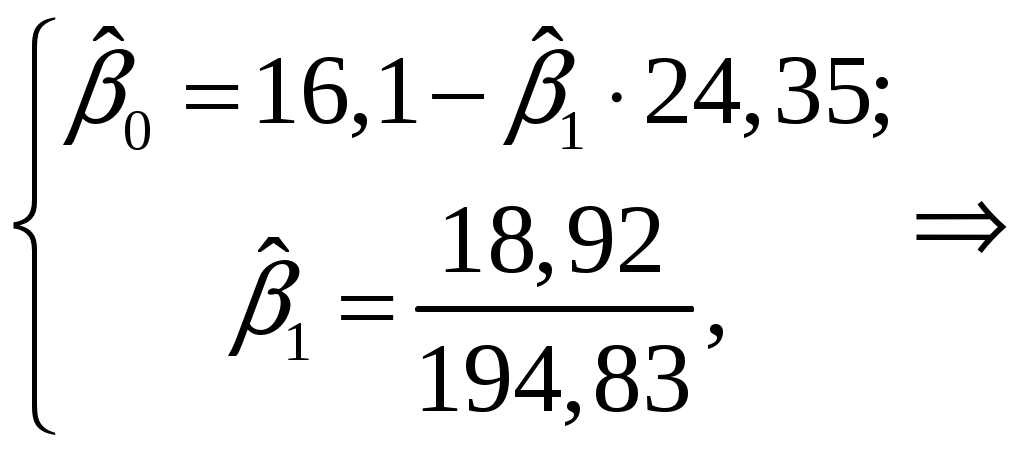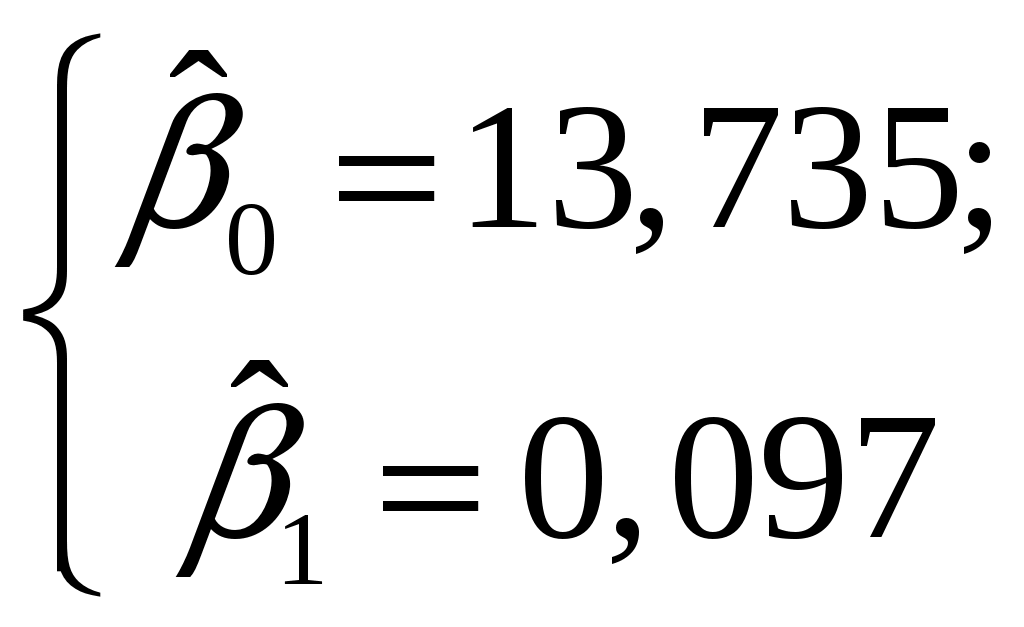



Получим: Подставим найденные параметры в уравнение получим:

.

5. 
   Проверьте значимость оценок коэффициентов и с надежностью 0,95 с помощью t-статистики Стьюдента и сделать выводы о значимости этих оценок. Значимо ли уровень образования влияет на заработок?
   

Оценку статистической значимости параметров регрессии и
корреляции проведем с помощью статистики Стьюдента и путем расчета доверительного интервала каждого из параметров.

Табличное значение критерия для числа степеней свободы
и уровня значимости α = 0,05 составит t_табл = 2,16.

Далее рассчитываем по каждому из параметров его стандартные ошибки: 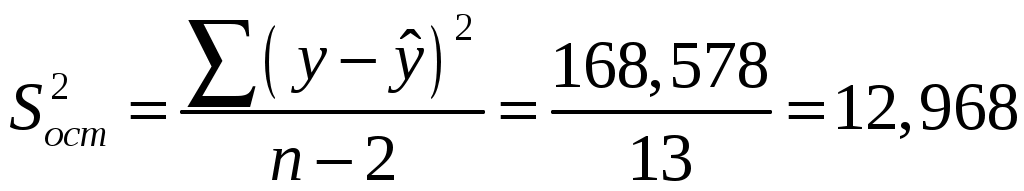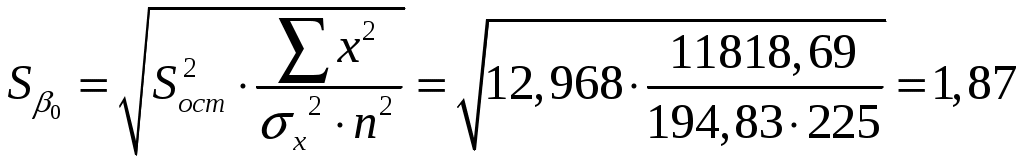, и .







Фактическое значение 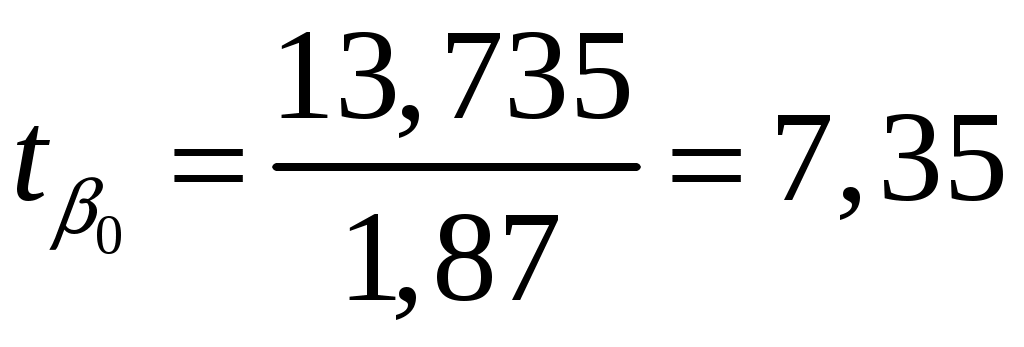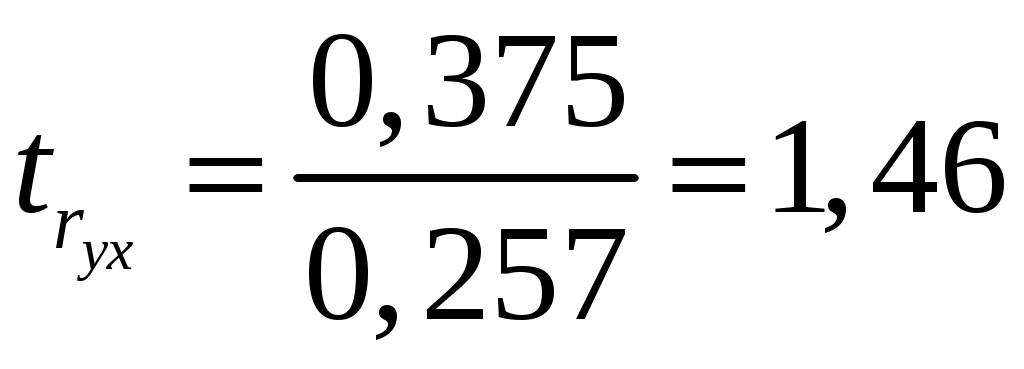статистик

, ,

Фактическое значения статистики превосходит табличное
значение: , поэтому параметр не случайно отличается от нуля, а статистически значим.

Фактические значения статистики не превосходят табличное
значение: ; , поэтому параметры и случайно отличаются от нуля, и статистически не значимы.

6. 
   Определите интервальные оценки коэффициентов и с надежностью 0,95. Сделайте вывод о точности полученных оценок коэффициентов.
   

Рассчитаем доверительные интервалы для параметров регрессии и . Для этого определим предельную ошибку для каждого показателя:





Доверительные интервалы:

и

Анализ верхней и нижней границ доверительного интервала
приводит к выводу о том, что с вероятностью параметр , находясь в указанных границах, не принимает нулевого значения, т.е. является статистически значимым и существенно отличным от нуля.

и

Анализ верхней и нижней границ доверительного интервала
приводит к выводу о том, что с вероятностью параметр , находясь в указанных границах, принимает нулевое значение, т.е. является статистически не значимым и не существенно отличным от нуля.

7. 
   Рассчитаем стандартную ошибку регрессии. Сделайте вывод о точности полученного уравнения регрессии.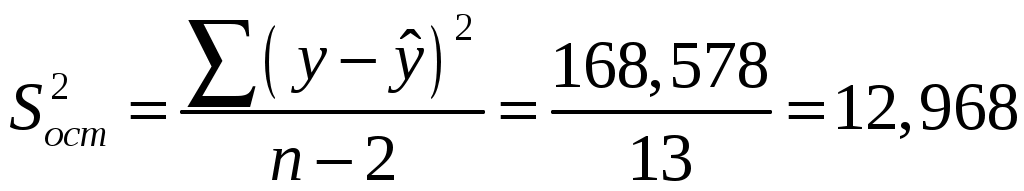
   

Качество модели, исходя из относительных отклонений по каждому
наблюдению, признается удовлетворительным.

8. 
   Определим коэффициент детерминации R² и сделайте вывод о качестве подгонки уравнения регрессии к исходным данным.
   

Коэффициент детерминации определяется по формуле: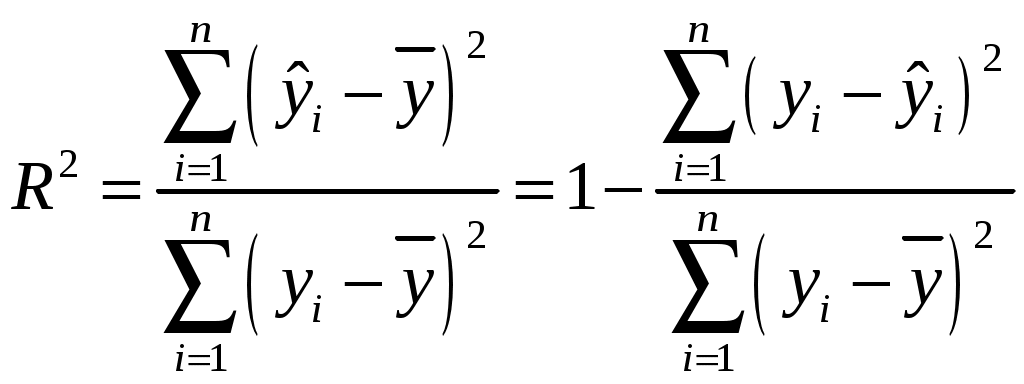



Вычислим: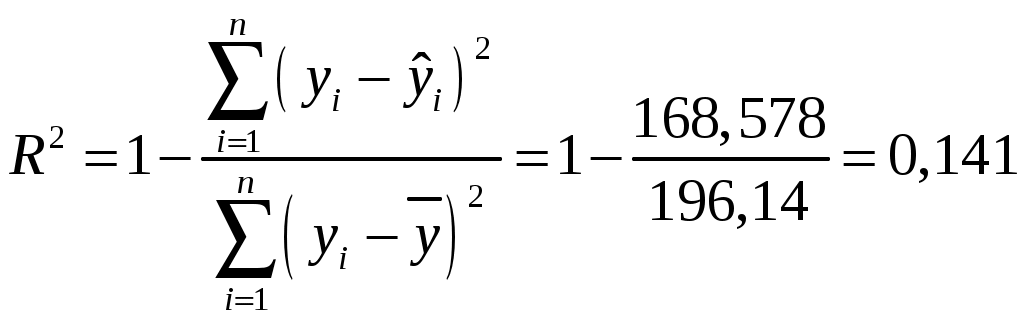



Множественный коэффициент детерминации , показывает, что около 14,1% вариации зависимой переменной учтено в модели и обусловлено влиянием включенного фактора и на 85,9% — другими факторами, не включенными в модель.

9. 
   Рассчитайте среднюю ошибку аппроксимации и сделайте выводы о качестве уравнения регрессии.
   

Средняя ошибка аппроксимации по формуле: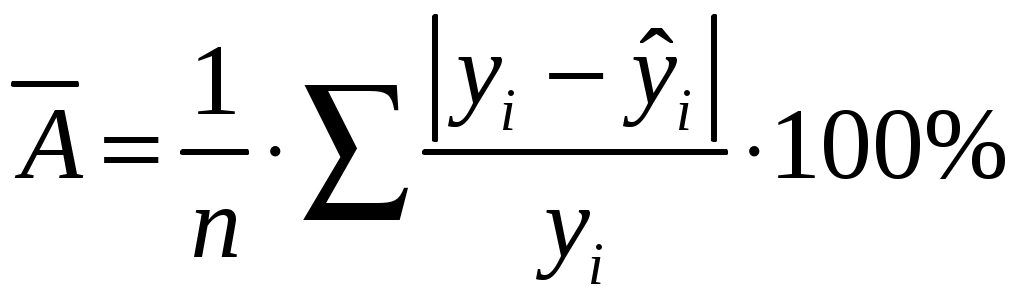



Найдем величину средней ошибки аппроксимации :

.

В среднем, расчетные значения отклоняются от фактических на 18,44% поскольку ошибка больше 7%, то данное уравнение не рекомендуется использовать в качестве регрессии.

10. 
    Рассчитайте прогнозное значение результата , если значение фактора X будет больше на 15% его среднего уровня .
    

Если прогнозное значение фактора X будет больше на 15% его среднего уровня и составит: лет, тогда индивидуальное прогнозное значение часового заработка одного рабочего составит:

11. 
    Дайте экономическую интерпретацию коэффициентов парной регрессии.
    

.

Параметр показывает, что с увеличением общего стажа работы после окончания учебы на 1 год часовой заработок одного рабочего возрастает в среднем на 0,097 долл./час.