Физика. Контрольная работа по дисциплине Физика Вариант 1 студент группы
 Скачать 107.89 Kb. Скачать 107.89 Kb.
|
|
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Тульский государственный университет» Интернет-институт ТулГУ
КОНТРОЛЬНАЯ РАБОТАпо дисциплине «Физика»Вариант № 1
Тула 2019 Содержание Задача № 1 2 Задача № 2 4 Задача № 3 6 Задача № 4 7 Задача № 5 7 Список использованных источников 9 Задача № 1Условие: Материальная точка начинает двигаться из начала координат в момент времени t0 = 0 с нулевой начальной скоростью и ускорением, изменяющимся со временем по закону 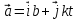 , где b=3 м/с2, k = 12м/с3. На каком расстоянии от начала координат окажется точка через время t=1c? , где b=3 м/с2, k = 12м/с3. На каком расстоянии от начала координат окажется точка через время t=1c? Решение: Если ускорение материальной точки изменяется по закону 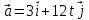 то для проекций ускорения на координатные оси имеем [2, c. 107] 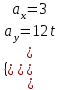 для проекций скорости на координатные оси имеем 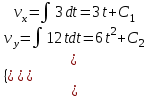 Если в начальный момент времени скорость точки была нулевой, то нулевыми были и проекции скорости на координатные оси. Тогда 3t+C1=0, 6t2+C2=0 откуда С1=0, С2=0 и  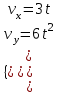 Для проекций радиус-вектора точки на координатные оси имеем [2, c. 110] 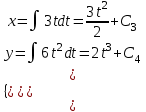 Если в начальный момент времени точка находилась в начале координат, то 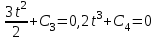 откуда С3=0, С4=0 и откуда С3=0, С4=0 и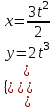 В момент времени t=1 с точка будет иметь координаты x=3/2 (м), y=2 (м) и находиться на расстоянии 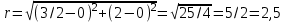 (м). (м).Ответ: r=2,5 м. Задача № 2Условие: Сформулировать уравнения движения частицы массы m: а) в проекциях на оси x,y,z декартовой системы координат; б) в проекциях на направления касательной и нормали к траектории. Консервативна ли сила 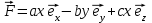 ? В случае положительного ответа найти потенциальную энергию U(x,y,z). ? В случае положительного ответа найти потенциальную энергию U(x,y,z). Решение: Для материальной точки (частицы) с постоянной массой m второй закон Ньютона в векторной форме имеет вид [2, c. 58] 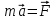 где 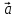 - ускорение материальной точки, - ускорение материальной точки, 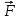 - равнодействующая сил, приложенных к ней. - равнодействующая сил, приложенных к ней.а) В проекциях на оси декартовой прямоугольной системы координат в пространстве уравнение равносильно, например, такой системе уравнений: 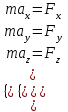 При этом 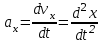 , ,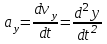 , , 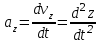 б) В проекциях на оси естественного координатного триэдра (касательная, главная нормаль, бинормаль к траектории в текущем положении материальной точки) уравнение равносильно такой системе уравнений [2, c. 65]: 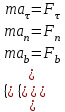 При этом 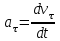 , , 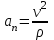 , , 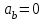 где ρ - радиус кривизны траектории. где ρ - радиус кривизны траектории.Рассмотрим силу 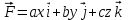 Обозначим P=ax, Q=by, R=cz. Тогда 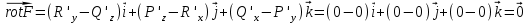 Значит, сила F является консервативной (потенциальной). Чтобы найти потенциал U(x,y,z) составим систему уравнений с частными производными [2, c. 85]: 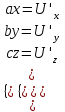  Интегрируя первое уравнение системы по x получим 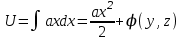 (здесь роль постоянной интегрирования играет любая функция φ(y,z) так как её частная производная по x равна нулю). Далее дифференцируем полученную функцию U по переменной y используя второе равенство системы. Получим 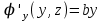 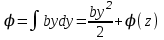 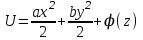 И наконец, используя третье уравнение системы, получим 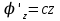 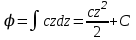 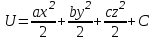 Задача № 3Условие: Определить величины 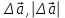 и ∆а , соответствующие изменению направления вектора а на противоположное. и ∆а , соответствующие изменению направления вектора а на противоположное. Решение: 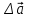 - приращение вектора - приращение вектора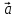 , , 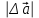 - модуль этого приращения, ∆а= - модуль этого приращения, ∆а=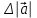 - приращение модуля вектора - приращение модуля вектора 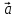 [1, c. 69]. [1, c. 69].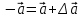 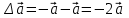 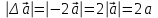 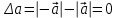 Ответ: 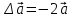 , , 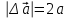 , , 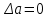 Задача № 4Условие: Колесо вращается вокруг своей оси симметрии так, что зависимость угла поворота радиуса колеса от времени дается уравнением ϕ = Аt + Bt2 + Ct3 , где А=2 рад/с, В=0,5 рад/с2 , С=0,5рад/с3 . Найти радиус R колеса, если в момент времени t=2 c нормальное ускорение точки на ободе колеса равно an=36 м/с2. Решение: Если угол поворота колеса изменяется по закону: 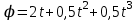 То его угловая скорость – по закону [1, c. 98] 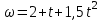 И в момент времени t=2 с составляет 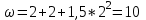 рад/с рад/сПоскольку для нормального ускорения точек обода колеса имеет место формула [1, c. 99]: 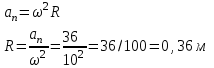 Ответ: R=0,36 м. Задача № 5Условие: Найти для идеального газа уравнение такого процесса, при котором теплоемкость газа изменяется с температурой по закону С = α /Т , где α = const. Решение: Процесс не политропный. Поэтому применив первое начало термодинамики в форме 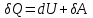 . .для одного моля газа: 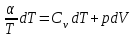 Используя уравнение Менделеева-Клапейрона перепишем это уравнение в виде [2, c. 328] 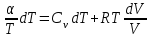 Разделив левую и правую части на RT, после интегрирования получаем 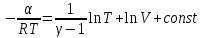 . .Отсюда находим искомое уравнение процесса: 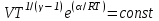 . .Ответ: 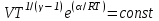 Список использованных источников1. Ботаки А.А., Ульянов В.Л., Ларионов В.В., Поздеева Э.В. Основы физики: учебное пособие. – Томск: Изд-во ТПУ, 2015. – 104 с. 2. Детлаф А.А., Яворский Б.М. Курс физики: учебное пособие для втузов. – 4-е изд., испр. – М.: Высш. шк., 2013. – 718 с. |
