Leonovich - копия. Контрольная работа по дисциплине кга в кми студента Трубач Д. В. гр.993041 Задание 1
 Скачать 217.37 Kb. Скачать 217.37 Kb.
|
Министерство образования Республики Беларусь Учреждение образования БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ
Контрольная работа по дисциплине КОМБИНАТОРНО-ГЕОМЕТРИЧЕСКИЕ АЛГОРИТМЫ В КОДИРОВАНИИ МУЛЬТИМЕДИЙНОЙ ИНФОРМАЦИИ Вариант №2
Минск 2022 Контрольная работа по дисциплине КГА в КМИ Студента_ Трубач Д.В. гр.№ 993041 Задание 1 Построить поле 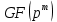 p =2, m = 3 / f(x) = p =2, m = 3 / f(x) = 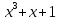 (пособие В. Д. Колесник «Кодирование и декодирование сообщений» (Алгебраическая теория блоковых кодов)», методические материалы) Построить таблицы сложения и умножения в заданном поле Построить матрицы дискретного преобразования Фурье в заданном поле Провести кодирование случайного вектора дискретным преобразованием Фурье в заданном поле Построить взаимные ортогональные латинские квадраты MOLS, используя таблицы сложения и умножения в заданном поле (см. лекции) Привести пример кодирования информации латинскими квадратами Определить структуру треугольника Паскаля заданного размера 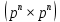 p=2, n=4 p=2, n=4Определить матрицы треугольника Паскаля (прямую и обратную) в конечном поле mod p Провести кодирование и декодирование случайного вектора с помощью с помощью матричного преобразования Паскаля По матрице Паскаля построить код Рида-Маллера и схемы кодирования и декодирования Построить решетку по заданной генераторной матрице 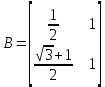 =[1/2 1; (sqrt(3)+1)/2 1] =[1/2 1; (sqrt(3)+1)/2 1]Определить параметры построенной решетки. Студент _________________________ Преподаватель _____________________ «______» _____________________2022___ Выполним необходимые расчеты в среде математического моделирования MathworksMatlab R2021b. Полный листинг программы приведен в приложении А. 1. Построить поле GF(pm) p = 2, m = 3 / f(x) = x3 + x + 1. % очищаем рабочую область clc; close all; clear; m = 3; % степень двойки n = 2^m; % количество элементов поля fx = 11; % ген.полином x^3+x+1, в двоичном виде: 1011, в десятичном: 11 % строим поле: elem = 0:n-1; % элементы поля f = gf(elem,m,fx) % создаем поле Галуа 2^3
2. Построить таблицы сложения и умножения в заданном поле. % таблицы сложения и умножения etb = repmat(f ,n,1); % таблица элементов поля fprintf("Таблица сложения:") addtb = etb + etb' % таблица сложения fprintf("Таблица умножения:") multb = etb .* etb' % таблица умножения
3. Построить матрицы дискретного преобразования Фурье в заданном поле. Дискретная матрица преобразования Фурье является комплексной матрицей, матричное произведение которой с вектором вычисляет дискретное преобразование Фурье вектора. dftmtx берет БПФ единичной матрицы, чтобы сгенерировать матрицу преобразования. % построение матриц ДПФ и ОДПФ alph = gf(2,m,fx); % 2 - это первообразный корень в заданном поле fprintf("Матрица ДПФ:") dm = dftmtx(alph) % матрица прямого ДПФ в данном поле fprintf("Матрица ОДПФ:") idm = dftmtx(1/alph) % матрица обратного ДПФ в данном поле
4. Провести кодирование случайного вектора дискретным преобразованием Фурье в заданном поле. Прямое и обратное дискретное преобразование Фурье устанавливает взаимно однозначное соответствие между N отсчетами во временной области и N отсчетами в спектральной. Положим, что последовательность {x[n] = x(nTд), n = [0, 1, …, M – 1]} получена в результате дискретизации непрерывного сигнала с интервалом дискретизации, равным Tд с. Число N ≥ M определим, как размер (число точек, порядок) дискретного преобразования Фурье. Пара прямого и обратного преобразований Фурье запишется в следующем виде:
Здесь 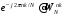 – базисные функции ДПФ. – базисные функции ДПФ.% кодирование случайного вектора в данном поле data = randi([0 2^m-1],1,n-1); % случайный вектор данных длинной 2^m-1 x = gf(data,m,fx); % переводим данные в поле fprintf("ДПФ:") y = x*dm % кодируем - делаем ДПФ данных
5. Построить взаимные ортогональные латинские квадраты MOLS, используя таблицы сложения и умножения в заданном поле % построение MOLS квадратов % заготовки из нулей L1 = gf(zeros(n,n),m,fx); L2 = gf(zeros(n,n),m,fx); alph = gf(2,m,fx); % 2 - это первообразный элемент в заданном поле betta = gf(6,m,fx); % 6 - это первообразный элемент в заданном поле for i = 1:n L1(i,:) = alph*f + f(i); L2(i,:) = betta*f + f(i); end
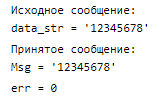
6. Привести пример кодирования информации латинскими квадратами. % кодирование сообщения латинскими квадратами L11 = double(L1.x) % значения квадрата в числовом формате L22 = double(L2.x) % значения квадрата в числовом формате mtxI = repmat((0:n-1)', 1,n); % матрица индексов строк mtxJ = repmat(0:n-1, n,1); % матрица индексов столбцов % полный алфавит кодовых слов: CODE = [mtxI(:), mtxJ(:), L11(:), L22(:)]; fprintf("Исходное сообщение:") data_str ='12345678' % исходное сообщение data_bin = dec2bin(data_str,6); % переводим в двоичный вид code = []; % пустой массив под сообщение for i = 1:length(data_str) % разбиваем байты на куски по 3 бита и переводим в десятичный вид - это % будут индексы квадрата idx_i = bin2dec( data_bin(i,1:3) ); % старшие 3 бита idx_j = bin2dec( data_bin(i,4:6) ); % младшие 3 бита S1 = L11(idx_i+1,idx_j+1); % значение из первого квадрата (прибавляем единицу т.к. нумерация массивов с 1) S2 = L22(idx_i+1,idx_j+1); % значение из второго квадрата (прибавляем единицу т.к. нумерация массивов с 1) code = [code, dec2bin(idx_i,3), dec2bin(idx_j,3), dec2bin(S1,3), dec2bin(S2,3)]; %#ok end S = code - '0'; % переводим в числовой формат % передача % действие шума на сигнал nn = 3; % количество испорченных бит noise = randi(length(S),1,nn); % индексы "битых" бит Sn = S; Sn(noise) = Sn(noise); % инвертируем биты % приём SB = reshape(Sn,12,[])'; % разбиваем по блокам в 12 бит Sch = char(SB + '0'); % преобразуем в строковый формат (нужно для перевода из двоичной системы в десятичную) N = size(SB,1); % количество блоков Msg_temp = []; for i = 1:N fr = Sch(i,:); % берем один блок %fr_dec = fr - '0'; % из строкового формата преобразуем в числовой % нужно найти ближайшее из полного алфавита % классический алгоритм поиска минимума k = 1; minD = 1000; for ii = 1:size(CODE,1) % для каждого кодового слова в алфавите code_wrd = dec2bin( CODE(ii,:),3 ); % переводим в двоичный формат code_wrd = reshape(code_wrd',1,[]); % вытягиваем в одну строку R = code_wrd - fr; % посимвольные разности кодового слова алфавита и принятого слова dist = sqrt( sum( R.^2 ) ); % корень из суммы квдратов разностей (расстояние) if dist < minD % если полученное расстояние меньше минимума k = ii; % сохраняем индекс minD = dist; % сохраняем значение минимума end end % k - это индекс ближайшего кодового слова I = dec2bin(CODE(k,1), 3); % переводим в двоичный код J = dec2bin(CODE(k,2), 3); % bindata = [I, J]; % соединяем блоки decdata = bin2dec(bindata); % переводим в десяточный формат Msg_temp = [Msg_temp, decdata]; % собираем сообщение %Msg = [Msg, char(decdata)]; % переводим в символ и собираем сообщение End Msg_bin = []; % пустой массив под сообщение Msg_dec = []; Msg_bin = dec2bin( Msg_temp,8 ); Msg_dec = bin2dec(Msg_bin); Msg = reshape(char(Msg_dec)',1,[]); % вытягиваем и переводим в символы fprintf("Принятое сообщение:") Msg err = sum( Msg=data_str ) % количество неправильно принятых символов
7. Определить структуру треугольника Паскаля заданного размера (pn × pn ), p = 2, n = 4. Треугольник Паскаля – это геометрическое расположение биноминальных коэффициентов в треугольнике.
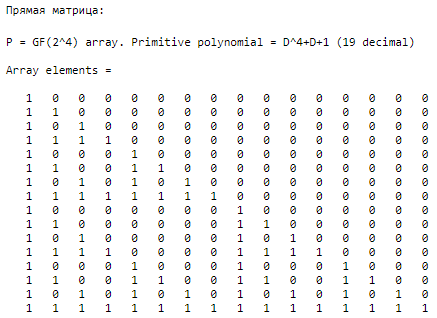
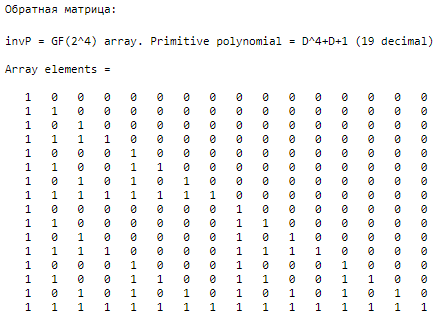
Каждое число в треугольнике Паскаля равно 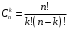 , где n – номер строки, k – номер столбца. , где n – номер строки, k – номер столбца.8. Определить матрицы треугольника Паскаля (прямую и обратную) в конечном поле mod p (p = 2). % матрица Паскаля p = 2; n = 4; pn = p^n; P = gf(eye(pn),n); % заготовка (единичная матрица) P(:, 1) = 1; % формируем матрицу Паскаля (в конечном поле) for j = 3:pn for i = 2:pn - 1 P(j, i) = P(j - 1, i - 1) + P(j - 1, i); end end fprintf("Прямая матрица:") P % прямая матрица fprintf("Обратная матрица:") invP = inv(P) % обратная матрица
9. Провести кодирование и декодирование случайного вектора с помощью матричного преобразования Паскаля. Элементы матричного преобразования Паскаля получаются непосредственно из записей прямой матрицы Паскаля путем чередования знаков столбцов. Кодирование случайного вектора проведем по формуле 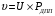 . Декодирование производится по формуле . Декодирование производится по формуле 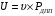 . .% кодировние и декодирование матрицей Паскаля fprintf("Исходное сообщение:") str = 'целая строка' % исходное сообщение data_bin = dec2bin(str,16)' - '0'; % переводим символы в числовой двоичный формат data = data_bin(:); % вытягиваем в один столбец N = length(data); % длинна сообщения r = rem(N,pn); % остаток от деления длин сообщенияна размер матрицы if r = 0 % если размеры не кратны data = [data zeros(1,pn-r)]'; % дополняем нулями end B = reshape(data,pn,[]); % упаковываем сообщение в блоки, по размеру матрицы Паскаля Cd = P*B; % кодируем (умножаем на прямую матрицу)) Cd = Cd(:)'; % вытягиваем результат в одну строку % декодирование B = reshape(Cd,pn,[]); % поток данных нарезаем на куски сообразно размеру матрицы d = invP*B; % декодирование (умножаем на обратную матрицу) dd = double(d.x); % переводи в числовой формат dd = dd(:)'; % вытягиваем в строку sbin = char(dd + '0'); % переводим в символьный формат Sbin = reshape(sbin,16,[])'; % собираем в блоки по 16 бит Msg = char( bin2dec(Sbin)' ); % переводдим в десятичный формат и затем в символы fprintf("Принятое сообщение:") Msg % принятое сообщение
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ [1] Колесник, В.Д. Кодирование и декодирование сообщений (Алгебраическая теория блоковых кодов) : учебное пособие / В.Д. Колесник [и др.]. – Санкт-Петербург, 2005. [2] Моделирование алгоритмов быстрой обработки сигналов в инфокоммуникационных сетях : учебно-методическое пособие / С. Б. Саломатин. – Минск : БГУИР, 2016. – 132 с. : ил. [3] Камерон, П. Теория графов. Теория кодирования и блок-схемы / П. Камерон, Дж. Ван Линт. – М.: Наука, 1980. – 144 с. : ил. Приложение А (обязательное) Листинг исходной программы % очищаем рабочую область clc; close all; clear m = 3; % степень двойки n = 2^m; % количество элементов поля fx = 11; % ген.полином x^3+x+1, в двоичном виде: 1011, в десятичном: 11 % 1) строим поле: elem = 0:n-1; % элементы поля f = gf(elem,m,fx) % создаем поле Галуа 2^3 % 2) таблицы сложения и умножения etb = repmat(f ,n,1); % таблица элементов поля fprintf("Таблица сложения:") addtb = etb + etb' % таблица сложения fprintf("Таблица умножения:") multb = etb .* etb' % таблица умножения % 3) построение матриц ДПФ и ОДПФ alph = gf(2,m,fx); % 2 - это первообразный корень в заданном поле fprintf("Матрица ДПФ:") dm = dftmtx(alph) % матрица прямого ДПФ в данном поле fprintf("Матрица ОДПФ:") idm = dftmtx(1/alph) % матрица обратного ДПФ в данном поле % 4) кодирование случайного вектора в данном поле data = randi([0 2^m-1],1,n-1); % случайный вектор данных длинной 2^m-1 x = gf(data,m,fx); % переводим данные в поле fprintf("ДПФ:") y = x*dm % кодируем - делаем ДПФ данных % 5) построение MOLS квадратов % заготовки из нулей L1 = gf(zeros(n,n),m,fx); L2 = gf(zeros(n,n),m,fx); alph = gf(2,m,fx); % 2 - это первообразный элемент в заданном поле betta = gf(6,m,fx); % 6 - это первообразный элемент в заданном поле for i = 1:n L1(i,:) = alph*f + f(i); L2(i,:) = betta*f + f(i); end L1 L2 % проверка ортогональности: %cmp = double(L1.x)*1i + double(L2.x); % объединяем элементы в пары %[length(unique(cmp)), n^2] % сравниваем количество уникальных пар и размер квадрата % 6) кодирование сообщения латинскими квадратами L11 = double(L1.x) % значения квадрата в числовом формате L22 = double(L2.x) % значения квадрата в числовом формате mtxI = repmat((0:n-1)', 1,n); % матрица индексов строк mtxJ = repmat(0:n-1, n,1); % матрица индексов столбцов % полный алфавит кодовых слов: CODE = [mtxI(:), mtxJ(:), L11(:), L22(:)]; fprintf("Исходное сообщение:") data_str ='12345678' % исходное сообщение data_bin = dec2bin(data_str,6); % переводим в двоичный вид code = []; % пустой массив под сообщение for i = 1:length(data_str) % разбиваем байты на куски по 3 бита и переводим в десятичный вид - это % будут индексы квадрата idx_i = bin2dec( data_bin(i,1:3) ); % старшие 3 бита idx_j = bin2dec( data_bin(i,4:6) ); % младшие 3 бита S1 = L11(idx_i+1,idx_j+1); % значение из первого квадрата (прибавляем единицу т.к. нумерация массивов с 1) S2 = L22(idx_i+1,idx_j+1); % значение из второго квадрата (прибавляем единицу т.к. нумерация массивов с 1) code = [code, dec2bin(idx_i,3), dec2bin(idx_j,3), dec2bin(S1,3), dec2bin(S2,3)]; %#ok end S = code - '0'; % переводим в числовой формат % передача % действие шума на сигнал nn = 3; % количество испорченных бит noise = randi(length(S),1,nn); % индексы "битых" бит Sn = S; Sn(noise) = Sn(noise); % инвертируем биты % приём SB = reshape(Sn,12,[])'; % разбиваем по блокам в 12 бит Sch = char(SB + '0'); % преобразуем в строковый формат (нужно для перевода из двоичной системы в десятичную) N = size(SB,1); % количество блоков Msg_temp = []; for i = 1:N fr = Sch(i,:); % берем один блок %fr_dec = fr - '0'; % из строкового формата преобразуем в числовой % нужно найти ближайшее из полного алфавита % классический алгоритм поиска минимума k = 1; minD = 1000; for ii = 1:size(CODE,1) % для каждого кодового слова в алфавите code_wrd = dec2bin( CODE(ii,:),3 ); % переводим в двоичный формат code_wrd = reshape(code_wrd',1,[]); % вытягиваем в одну строку R = code_wrd - fr; % посимвольные разности кодового слова алфавита и принятого слова dist = sqrt( sum( R.^2 ) ); % корень из суммы квдратов разностей (расстояние) if dist < minD % если полученное расстояние меньше минимума k = ii; % сохраняем индекс minD = dist; % сохраняем значение минимума end end % k - это индекс ближайшего кодового слова I = dec2bin(CODE(k,1), 3); % переводим в двоичный код J = dec2bin(CODE(k,2), 3); % bindata = [I, J]; % соединяем блоки decdata = bin2dec(bindata); % переводим в десяточный формат Msg_temp = [Msg_temp, decdata]; % собираем сообщение %Msg = [Msg, char(decdata)]; % переводим в символ и собираем сообщение End Msg_bin = []; % пустой массив под сообщение Msg_dec = []; Msg_bin = dec2bin( Msg_temp,8 ); Msg_dec = bin2dec(Msg_bin); Msg = reshape(char(Msg_dec)',1,[]); %вытягиваем и переводим в символы fprintf("Принятое сообщение:") Msg err = sum( Msg=data_str ) % количество неправильно принятых символов % 7) матрица Паскаля p = 2; n = 4; pn = p^n; P = gf(eye(pn),n); % заготовка (единичная матрица) P(:, 1) = 1; % формируем матрицу Паскаля (в конечном поле) for j = 3:pn for i = 2:pn - 1 P(j, i) = P(j - 1, i - 1) + P(j - 1, i); end end % 8) матрицы Паскаля fprintf("Прямая матрица:") P % прямая матрица fprintf("Обратная матрица:") invP = inv(P) % обратная матрица % 9) кодировние и декодирование матрицей Паскаля fprintf("Исходное сообщение:") str = 'целая строка' % исходное сообщение data_bin = dec2bin(str,16)' - '0'; % переводим символы в числовой двоичный формат data = data_bin(:); % вытягиваем в один столбец N = length(data); % длинна сообщения r = rem(N,pn); % остаток от деления длин сообщенияна размер матрицы if r = 0 % если размеры не кратны data = [data zeros(1,pn-r)]'; % дополняем нулями end B = reshape(data,pn,[]); % упаковываем сообщение в блоки, по размеру матрицы Паскаля Cd = P*B; % кодируем (умножаем на прямую матрицу)) Cd = Cd(:)'; % вытягиваем результат в одну строку % декодирование B = reshape(Cd,pn,[]); % поток данных нарезаем на куски сообразно размеру матрицы d = invP*B; % декодирование (умножаем на обратную матрицу) dd = double(d.x); % переводи в числовой формат dd = dd(:)'; % вытягиваем в строку sbin = char(dd + '0'); % переводим в символьный формат Sbin = reshape(sbin,16,[])'; % собираем в блоки по 16 бит Msg = char( bin2dec(Sbin)' ); % переводдим в десятичный формат и затем в символы fprintf("Принятое сообщение:") Msg % принятое сообщение |

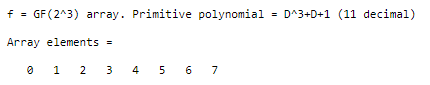




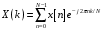 , k = 0:N – 1;
, k = 0:N – 1;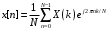 , n = 0:N – 1;
, n = 0:N – 1;